基于COMSOL的多金属耦合腐蚀行为仿真

石鹏飞,段国庆,郭 倩,杨文山,卢云飞

(武汉第二船舶设计研究所,武汉 430064)

海洋结构物使用的金属种类繁多,由于各金属材料间存在电化学活性差异,极易形成电偶腐蚀[1]。长期以来,国内外学者对海洋环境中的电偶腐蚀进行了大量的研究,其研究对象主要集中于两种金属电连接形成的双金属耦合体系[2-5],对于3种及以上的多金属耦合体系研究鲜有报道[6-7]。

对于双金属电偶体系,根据混合电势理论[8],阳极金属自腐蚀电位低,阴极金属自腐蚀电位高。同理,在多金属电偶体系中,自腐蚀电位高的金属作为阴极,自腐蚀电位低的金属作为阳极,但对于中间自腐蚀电位的金属的阴阳极状态一直没有较为明确的判定方法。电偶腐蚀是一种不均匀腐蚀类型,在靠近阴阳极接触点附近的阳极区腐蚀程度较严重,而远离阴阳极接触点的阳极区腐蚀程度较轻。由于受到阴阳极面积比等很多因素影响,所以有必要引入数值模拟方法来研究复杂条件下的电偶腐蚀。

本工作通过将多金属耦合体系拆分成多个双金属耦合体系,采用COMSOL软件,对比分析了各双金属耦合体系间耦合电流的大小,提出了一种基于中间电位金属的多金属耦合腐蚀模型,用于判断其阴阳极状态。同时,以高强钢-B10 铜镍合金-TA2钛合金耦合体系为例,研究了金属相对位置与阴/阳极面积比对复杂电偶腐蚀行为的影响,以期为舰船海水介质系统复杂电偶体系中的腐蚀行为研究工作与实际工程应用提供理论依据。

1 试验

1.1 试验材料

试验材料为TA2钛合金(以下简称为TA2)、B10铜镍合金(以下简称为B10)和高强钢,TA2的化学成分(质量分数)为:0.10%C;0.29%Si;0.56%Mn;0.001%S;0.007%P;0.55%Cr;4.58%Ni;0.42%Mo;0.053%V;余量Fe。B10的化学成分(质量分数)为:0.02%C;10.5%Ni;1.7%Fe;0.8%Mn;0.01%Pb;0.01%S;0.05%Zn;0.02%P;余量Cu。高强钢的化学成分(质量分数)为:0.10%C;0.15%Si;0.3%Fe;0.20%O;0.015%H;余量Ti。

1.2 电化学测试

依据GB/T 24196-2009《金属和合金的腐蚀电化学试验方法 恒电位和动电位极化测量导则》标准,对TA2、B10和高强钢进行动电位极化曲线测试,测得的极化曲线作为仿真模拟过程中的边界条件。试验采用三电极体系,参比电极为饱和甘汞电极(SCE),辅助电极为铂电极,测试试样的工作面积为1 cm2,试验溶液为青岛海域天然海水,采用恒温槽控制溶液温度为25℃。3种材料试样为工作电极。电位扫描范围为-300～350 mV(相对于开路电位),扫描速率为0.333 3 mV/s,试验测得的电位均相对于SCE。试验前,采用环氧树脂将试样进行固封,然后进行打磨、抛光、清洗和吹干后,置于干燥皿内保存待用。

2 多金属耦合腐蚀仿真

2.1 仿真控制方程

多金属耦合后,各电极之间的电位差会诱使电解质溶液中腐蚀电场的形成,处于腐蚀电场中的任意粒子i 的传输均满足Nernst-Planck 方程,如式(1)所示。

式中:Di为粒子i的扩散系数;Ci为粒子i 的浓度;Zi为粒子i所带电荷数;μi 为粒子i的迁移率;F 是法拉第常数;φ 是电解质电位;U 是溶液流动速率。

根据Fick第二扩散定律,式(1)左右两边同时对时间t求导,得到式(2)。

本工作将考虑以下假设:

(1) 电解质溶液充分混合,离子浓度均匀的,不存在浓度梯度,即无扩散现象(∂Ci/∂t=0);

(2) 电解质溶液不可压缩,不考虑对流对离子传质的影响(U=0);

(3) 电解质溶液呈电中性,总电荷量为零(▽Ci=0)。

根据以上假设,式(2)可以整理为式(3)。

上述方程表明φ 满足Laplace方程,表征了电解中质溶液中电位的分布,此处忽略了扩散和对流对质量传输的影响。

2.2 边界条件

求解电偶腐蚀过程模型时,电极表面的边界条件是求解腐蚀速率的关键。在金属电极表面,电流密度J 和电位满足式(4)。

式中:n0表示电极表面外法线方向;σ 为电解质电导率。

一般情况下,除了在极简单几何模型和恰当简化条件下,几乎不可能得到电流密度J(φ)的解析解。电流密度J 与φ 的关系式有很多种,包括简单的Tafel直线关系和Butter-Volmer关系,或者是实际测得的电位-电流密度极化曲线关系。本工作以实际测得的极化曲线作为边界条件。

对于不极化电极,电位是个固定值。对于金属表面涂层,其电流为零。总结以上边界条件如表1所示。

表1 边界条件Tab.1 Boundary conditions

2.3 多金属耦合体系中阴、阳极的判断

对于多金属耦合体系,通过混合电势理论,可知耦合电位Ecouple和耦合电流Ig。相对于双金属耦合体系中的阴、阳极,对于多金属耦合体系中处于中间电位的电极,无法直接确定其在整个体系中的阴、阳极状态。

假设有n 种金属电极(分别为M1,M2,…,Mn,n≥3),他们相互连接共同存在于电解质溶液中,其自腐蚀电位排序为M1的自腐蚀电位(Ecorr,1)＜M2的自腐蚀电位(Ecorr,2)＜…＜Mn的自腐蚀电位(Ecorr,n)。根据混合电位理论可知,在多金属耦合体系中,自腐蚀电位最负的金属M1为阳极,自腐蚀电位最正的金属Mn为阴极,自腐蚀电位居中的金属Mx(1＜x＜n)既可能为阴极,也可能为阳极。

为判断多金属体系中自腐蚀电位居中的金属Mx的阴、阳极状态,可以金属Mx为基准,将多金属体系拆分成(n-1)对双金属电偶体系,得到(x-1)对金属Mx作为阴极的双金属电偶体系,得到(n-x-2)对金属Mx作为阳极的双金属电偶体系。如表2所示,若金属Mx作为阴极的双金属电偶体系中,其耦合电偶之和大于金属Mx作为阳极的双金属电偶体系中的耦合电偶之和,则金属Mx表面得到电子,在整个金属耦合体系中,金属Mx则作为阴极,反之则为阳极。

表2 多金属耦合体系中金属Mx 阴、阳极状态判断方法Tab.2 Cathode and anode state judgment method of metal Mx of multi-metal coupling system

3 三金属耦合体系仿真

3.1 TA2、B10和高强钢的动电位极化曲线

由图1 可见,高强钢的自腐蚀电位最低,为-0.683 V,TA2的自腐蚀电位最高,为0.077 V,B10的自腐蚀电位居中,为-0.265 V。所以在此三金属电偶体系中TA2作为阴极,高强钢作为阳极,B10有可能作为阴极,也可能作为阳极。

图1 TA2、B10和高强钢在天然海水中的动电位极化曲线Fig.1 Potentiodynamic polarization curves of TA2,B10 and high strength steel in natural seawater

3.2 TA2、B10与高强钢的阴、阳极状态

参照2.3节中所述的策略,根据混合电势理论,可将TA2-B10-高强钢耦合体系拆分成两组双金属电偶体系,分别为以B10为阴极的B10-高强钢电偶体系和以B10为阳极的B10-TA2电偶体系,通过判断两组电偶体系的耦合电流之和的大小,便可判断出B10的阴、阳极状态。

如图2所示,TA2、B10和高强钢耦合体系有高强钢-B10-TA2、B10-高强钢-TA2和B10-TA2-高强钢等3种排布顺序,对比分析ITA2、B10与IB10、高强钢的大小关系,可判断B10电极表面净电流流出和流入的状态。

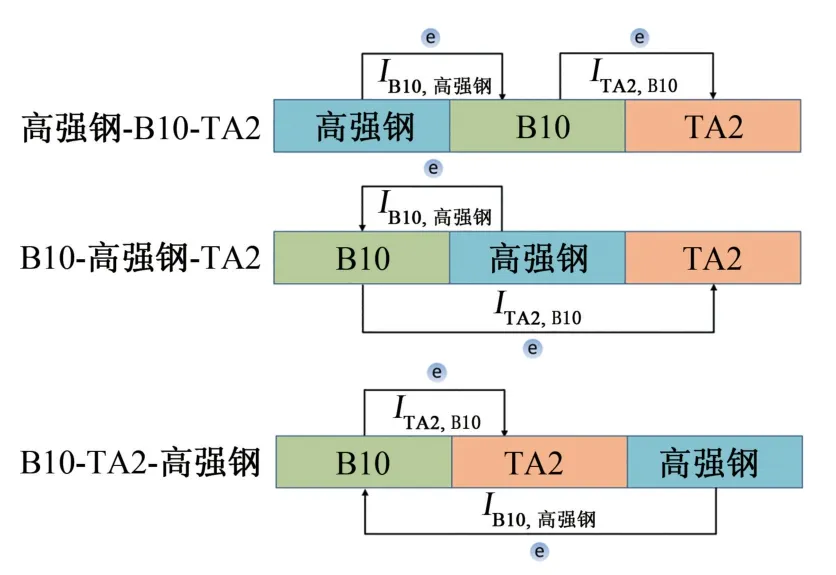
图2 TA2、B10和高强钢耦合体系不同电极排序示意Fig.2 Schematic diagram of defferent electrode ordering of TA2,B10 and high strength steel coupling system

3.3 三金属耦合体系建模

如图3所示,a、b、c 分别为3种金属的长度,在三金属耦合体系计算模型中,边界1、2 和3 均为绝缘,边界4为金属电极,4个边界围成60 mm×30 mm(a+b+c=60 mm,d=30 mm)的模拟区域,区域内充满电解质。

图3 三金属耦合腐蚀模型的尺寸与网格划分示意Fig.3 Schematic diagram of size and grid division of trimetal coupling corrosion modeling

为了便于研究三金属耦合体系中电极间的面积比对电偶腐蚀的影响,设定各电极宽度方向为定值,改变长度值,可调整各电极长度的比例(a∶b∶c),即可实现电极阴/阳极面积比的变化,类比材料科学领域三元相图的构建过程,将3种金属长度占总长度的比例构成三角坐标系,如图4所示,w 表示电极面积占比,三角形内任意一点对应由3种金属按一定比例构成的三金属电偶体系(如点A),三角坐标轴上的点代表双金属电偶体系(如点B),三角坐标系顶点代表单金属体系(如点C)。同时,为简化计算,以4 mm 为基本步长,将三角形等分成36个成分点,三角坐标系坐标轴等分成27个成分点,,改变各电极的长度与排布顺序,穷举分析了91个三体系成分点情况下的电偶腐蚀行为。利用数学插值法,可获得对应耦合体系的电流密度,判断中间电位金属的阴、阳极状态,最终得到各金属长度(L)比例的变化对电偶电流密度的影响。

图4 三金属耦合体系构成的三角坐标系Fig.4 Trigonometric coordinate system composed of trimetal coupling system

4 结果与分析

4.1 TA2、B10和高强钢耦合体系阴阳极判断

依据图2的排序,根据三金属耦合体系模型,对三电极体系进行建模,在绝缘其中某一组分的情况下,对比分析B10-高强钢电偶的耦合电流IB10,高强钢和TA2-B10 电偶的耦合电流ITA2,B10,仿真计算结果如图5所示,在排列顺序和阴/阳极面积比均相同的条件下,IB10,高强钢均大于ITA2,B10,即B10表面的净电流均是流入的,这表明在该三金属耦合体系中,B10作为阴极参与腐蚀活动。

图5 不同电极排序条件下B10-高强钢与TA2-B10电偶的电流密度Fig.5 Current density of B10-high strength steel and TA2-B10 galvanic couples under the condition of different electrode ordering

4.2 复杂电偶电位和电流密度分布

4.2.1 阴/阳极面积比对三金属耦合体系腐蚀行为的影响

由图6和图7可见:当TA2面积占比为20%,B10和高强钢面积占比为80%时,无论是哪种排序的耦合体系,随着B10面积占比的增加,整个耦合体系的阴/阳极面积比随之增大,三金属耦合体系的电位逐渐升高,各电极表面电流密度逐渐增,表明电偶腐蚀程度加剧,三金耦合体系的腐蚀速率增大;当B10面积占比为20%,TA2 和高强钢面积占比为80%时,随着TA2面积占比的增加,耦合体系的阴/阳极面积比随之增加,整个耦合体系的电位逐渐升高,各电极表面电流密度也随之变大,三金属耦合体系的腐蚀速率增大;当高强钢面积占比为20%,TA2和B10面积占比为80%时,耦合体系中阴/阳极面积比恒定,但两种高电位金属TA2 与B10 的面积占比均不同,这会影响三金属耦合体系的耦合电位与电流密度,当耦合体系中阴/阳极面积比恒定时,随着耦合体系中高电位金属TA2面积占比的增大,三金属耦合体系电位整体减小,各电极表面电流密度也随之减小,电偶腐蚀程度减缓,耦合体系的腐蚀速率减小。

图6 不同电极排序和电极面积比条件下TA2,B10和高强钢耦合体系的电位分布Fig.6 Potential distribution of TA2,B10 and high strength steel coupling system under the condition of different electrode ordering and electrode area ratios

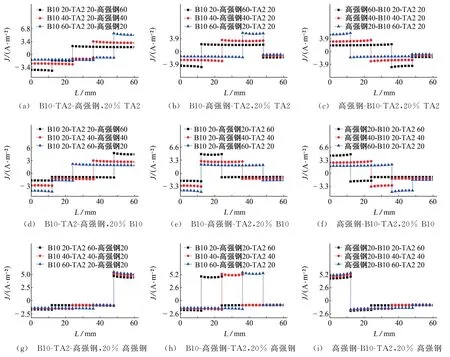
图7 不同电极排序和电极面积比条件下TA2,B10和高强钢耦合体系的电流密度分布Fig.7 Current density distribution of TA2,B10 and high strength steel coupling system under the condition of different electrode ordering and electrode area ratios

4.2.2 电极排序对三金属耦合体系腐蚀行为的影响

为研究各电极排序对三金属耦合体系腐蚀行为的影响,系统分析了恒定电极面积占比条件下,不同电极排序对低电位金属高强钢表面电位与电流密度的影响。

由图8可见:高强钢处于中间的排序时,高强钢表面的电位最大,电流密度也最大;B10处于中间的排序时,高强钢表面的电压和电流密度次之;TA2处于中间的排序时,高强钢表面的电位和电流密度最小,原因可能是当高强钢处于中间的排序时,两端的高电位金属B10与TA2对高强钢的电偶效应属于协同作用,同时,高电位金属B10与TA2间存在低电位金属高强钢,相互影响的效应较弱。

图8 不同电极排序条件下TA2,B10和高强钢耦合体系中高强钢表面的电位与电流密度分布Fig.8 Potential(a)and current density(b)distribution on the surface of high strength steel of TA2,B10 and high strength steel coupling system under the condition of different electrode ordering

4.2.3 耦合电位和电流密度分布

为研究阴/阳极面积比与电极排序对三金属耦合体系腐蚀行为的影响,系统研究了复杂体系中低电位金属高强钢表面的电流密度。

由图9可见:在高强钢-B10-TA 2排序条件下,耦合体系中高强钢表面的平均电流密度和最大电流密度的等高线图规律相似;当高强钢面积占比不变时,随着B10面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率也逐渐增大;当B10面积占比不变时,随着TA2面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率也逐渐增大;当TA2面积占比不变时,随着高强钢面积占比的增加,高强钢表面的平均电流密度逐渐减小,腐蚀速率也逐渐减小。

图9 高强钢-B10-TA2耦合体系中高强钢表面的平均电流密度和最大电流密度的等高线图Fig.9 Contour maps of average current density(a)and maximum current density(b)on the surface of high strength steel of high strength steel-B10-TA2 coupling system

由图10 可见:在B10-高强钢-TA2 排序条件下,耦合体系中高强钢表面的最大电流密度的等高线图与平均电流密度等高线图规律类似;当高强钢面积占比为10%左右时,高强钢表面的电流密度最大,腐蚀最严重;当B10面积占比不变时,随着TA2面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率越也逐渐增大;当高强钢面积占比不变时,随着B10占比增加,高强钢表面的平均电流密度逐渐增加,腐蚀速率逐渐增大;当TA2面积占比不变时,随着高强钢面积占比的增加,高强钢表面的平均电流密度逐渐减小,腐蚀速率逐渐降低。

图10 B10-高强钢-TA2耦合体系中高强钢表面的平均电流密度和最大电流密度的等高线图Fig.10 Contour maps of average current density(a)and maximum current density(b)on the surface of high strength steel of B10-high strength steel-TA2 coupling system

由图11可见:在B10-TA2-高强钢排序条件下,当高强钢面积占比为10%左右时,高强钢表面的电流密度最大,腐蚀最严重;当B10面积占比不变时,随着TA2面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率逐渐增大;当TA2面积占比不变时,随着高强钢面积占比的增加,高强钢表面的平均电流密度减小,腐蚀速率减小;当高强钢面积占比不变时,随着B10面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率逐渐增大,这与B10-高强钢-TA2排序条件下的规律类似。

图11 B10-TA2-高强钢耦合体系中高强钢表面的平均电流密度和最大电流密度的等高线图Fig.11 Contour map of average current density(a)and maximum current density(b)on the surface of high strength steel of B10-TA2-high strength steel coupling system

综上可知:在B10-TA2-高强钢排序条件下,不论电极面积比是多少,耦合体系中高强钢表面的平均电流密度均最小,腐蚀速率最小;在高强钢-B10-TA2排序条件下,耦合体系中高强钢表面的平均电流密度次之;在B10-高强钢-TA2排序条件下,耦合体系中高强钢表面的平均电流密度最大,腐蚀速率最大。

5 结论

(1) 通过将多金属耦合体系拆分为多个双金属电偶体系,对比分析了中间电位金属表面流入和流出的电流情况,从而能判断出其在体系中的阴、阳极状态。

(2) 对高强钢-B10铜镍合金-TA2钛合金耦合体系进行了仿真计算,在该耦合体系中,中间电位金属B10铜镍合金作为阴极参与电偶腐蚀。

(3) 在不同电极排序条件下,当高强钢面积占比不变时,随着TA2钛合金面积占比的增加,耦合体系中高强钢表面的平均电流密度逐渐减小,腐蚀速率逐渐减小,当B10铜镍合金面积占比不变时,随着TA2钛合金面积占比的增加,高强钢表面的平均电流密度逐渐增大,腐蚀速率越来越大。当TA2钛合金面积占比不变时,随着高强钢面积占比的增加,高强钢表面的平均电流密度减小,腐蚀速率减小。

(4) 不同电极排序的耦合体系中高强钢表面的腐蚀电流密度按从大到小的顺序依次为B10 铜镍合金-高强钢-TA2 钛合金、高强钢-B10 铜镍合金-TA2钛合金、B10铜镍合金-TA2钛合金-高强钢。