LTE系统中SPM校准算法
2022-12-03李光远柴远波郭志瑜
李光远 柴远波 孟 溪 郭志瑜 秦 勉
1(黄河科技学院 河南 郑州 450063)2(北京邮电大学 北京 100876)3(电信科学技术研究院无线移动通信国家重点实验室 北京 100191)4(郑州大学 河南 郑州 450001)5(河南大学 河南 开封 475001)
0 引 言
在长期演进(LTE)系统无线网络规划中,为了预测网络中的信号强度以及干扰情况,需要对无线信道中的传播模型进行预测。
传播模型的研究一直以来是无线通信中的一个基础课题,根据无线信道传播原理可将信道建模分为:大尺度衰落信道模型和小尺度衰落信道模型,以及射线跟踪模型[1-2]。大尺度传播模型主要有COST231路损模型、IMT-2000路损模型、IMT-Advanced路损模型、标准传播(SPM)校正路损模型。小尺度传播模型主要有IMT-2000小尺度信道模型,扩展空间(Spatial Channel Model Extension,SCME)小尺度模型。
如何准确有效地对路损模型进行建模,使传播模型尽可能贴近实际场景,以进行合理准确的网络规划,是目前研究的热点之一[1-6]。其中,标准传播模型应用较为广泛,具有较好的准确性和实用性[2]。校准过程中,根据在某个特定场景的测试结果,对参数进行校准。使用校正后的因子进行路损的计算,可以达到使传播模型尽量贴近实际场景的目的。
文献[7]给出了多斜率传播模型,文中根据理论值进行分段,但实际外场环境千变万化,为了更准确地对传播模型进行建模,本文提出基于中值线的分段标准传播模型。
许多情况下,都是采用最小二乘(LS,Least Squares)算法进行SPM校准的[7-9]。文献[8]进行最小二乘算法的求解时采用基于代价函数求导的方法,由于奇异值分解可以给出最小二乘最小范数解,因此本文提出基于奇异值分解的最小二乘SPM校准方法。为了降低计算复杂度,本文采用遗传算法进行SPM模型校准。遗传算法由Holland教授于1962年提出,并在1975年专著中详细阐述[10],之后广泛应用于参数估计、分词研究、5G等许多领域[11-14]。
1 分段校准的SPM传播模型
SPM模型是建立在Cost23l-Hata模型的基础上,SPM模型的表达式为[6]:
Pr=Ptx-[k1+k2lg(d)+k3lg(heff)+k4LDiffraction+
k5lg(heff)lg(d)+k6hmeff+kclutterf(clutter)]
(1)
式中:Pr为接收功率(单位:dBm);Ptx为发射功率(单位:dBm);k1为偏移常量(单位:dB);k2为距离相关的lg(d)的修正因子;d为接收机和发射机之间的距离;k3为lg(heff)的修正因子;heff为基站天线的有效高度(单位:m),与基站架高、地面高度因素有关;k4为衍射计算的修正因子;LDiffraction为阻隔路径上的衍射造成的损耗(单位:dB);k5为lg(heff)lg(d)的修正因子;k6为hmeff移动台有效高度的修正因子;hmeff为移动台的有效天线高度(单位:m),与终端高度、地面高度等因素有关;kclutter为f(clutter)的修正因子,f(clutter)是地貌的平均加权损耗。
对于分段标准传播模型,以两段为例可写成如下分段函数的形式:
式中:p0为分段点。
文献[7]中根据电磁传播理论确定p0=4hThR/λ,其中:hT为发射天线高度;hR为接收天线高度(单位:m);λ为波长。但实际外场环境千变万化,为了和外场实际情况更好地吻合,本文提出基于中值线的分段SPM校准方法。
基于中值线的分段SPM校正的基本流程如图1所示。
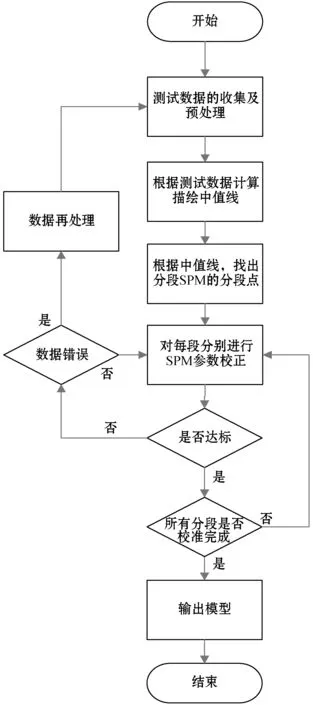
图1 分段SPM校准流程
首先对测试数据进行收集,去除无效数据。
根据测试数据描绘中值线,中值线的描绘方法为取等间隔距离的测试数据,然后求均值。
由中值线找出分段SPM的分段点,由中值线的转折点确定分段点P′,P′={p0,p1,…,pn}。
对每段分别进行SPM校准,然后判断校准是否达标,若不达标则返回重新校准,待达标后输出校准参数。
校正是一个不断调整的过程,在校正得出最终结果之前,采用以下标准来衡量对参数的调整是否结束。当满足以下条件时,认为校正可以结束[7-8]。
(1) 预测值和实测值误差的均值最小化,尽量为0,不大于0.2 dB。
(2) 预测值和实测值误差标准偏差小于8 dB。
2 SPM校准算法
2.1 基于奇异值分解的SPM校准
本文采用基于奇异值分解的LS算法[15],进行SPM模型校准。其基本思想如下:
对于线性方程组AX=b,A∈Rm×n(或Cm×n),则存在酉矩阵U∈Rm×n(或Cm×n)和V∈Rm×n(或Cm×n)使得:
A=UθVH
(3)
式中:θ=diag(σ1,σ2,…,σr,0,…,0),σ为矩阵A的奇异值。则A的Moore-Penrose广义逆矩阵G为:
G=Vθ+UH
(4)
式中:θ+=diag(1/σ1,1/σ2,…,1/σr,0,…,0),
因此,给出最小二乘最小范数解:
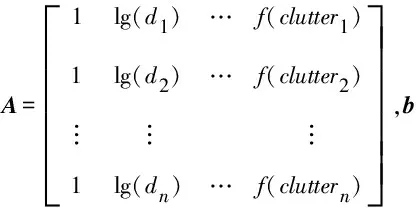
yi=Ptx-Pr
(6)
2.2 基于遗传算法的SPM校准
基于遗传算法的校准,本质上是解空间上进行二维搜索,因此得到的是局部最优解。遗传算法的实现过程一般包括六个步骤[10,13]:
(1) 确定解的染色体编码方法,即确定出个体的基因型表示方法及遗传算法的搜索空间。
(2) 随机产生初始种群,每个个体表示为染色体的基因编码。
(3) 确定个体适应度的量化评价方法,即确定出由目标函数值到个体适应度函数值的转化规则。
遗传算法适应度函数J(K)根据最小二乘算法可取为如下形式:
式中:f(di,k)=yi-AiK,i=1,2,…,n,K=(k1,k2,k3,k4,k5,k6,kclutter)T。
目标函数的解空间为:
Kj∈R,j=1,2,…,7{K:K∈R7}
判断是否符合优化准则,若符合,输出最优解,计算结束;否则转向步骤(4)继续。
(4) 设计遗传算子,产生新的个体。即确定选择运算、交叉运算、变异运算三种遗传运算的具体操作方法。
确定遗传算法的有关运行参数。一般包括:M,G,Pc,Pm。其中:M为种群规模,即群体中所含个体的数量;G为遗传算法的终止进化代数;Pc为交叉概率;Pm为变异概率。
Goldberg[16]在其专著中给出了一组较为合理的参数为:种群规模M:20~30;交叉概率Pc:0.75~0.95;变异概率Pm:0.005~0.010。
(5) 依据选择策略选择再生个体,返回到步骤(3)。
(6) 确定解码方法,即确定出个体基因型到个体表现型的对应关系。
3 实验结果与分析
仿真中使用的测试数据采集如图2所示。
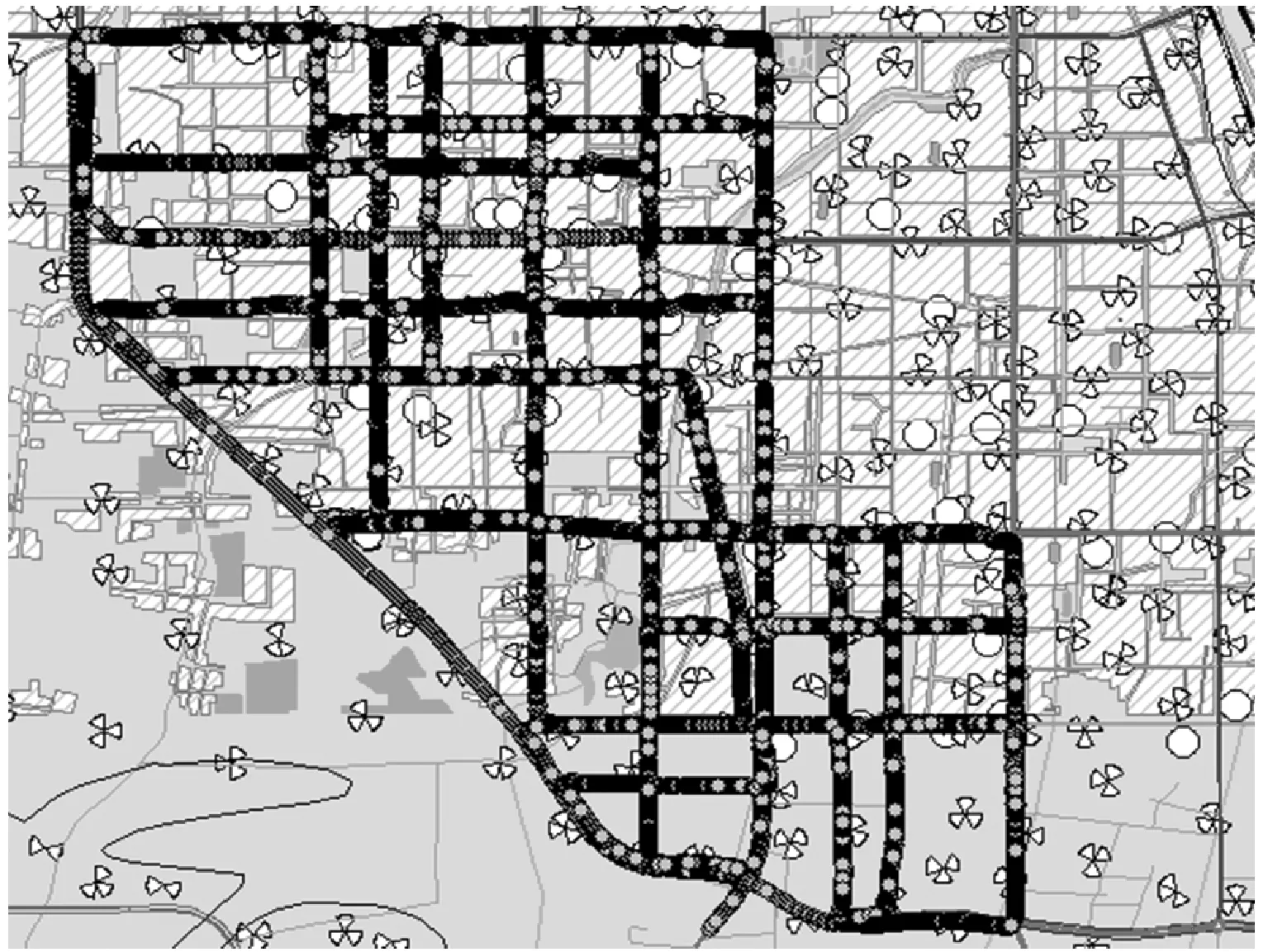
图2 测试路线
图2中测试路线位于郑州市区。表1给出了仿真所使用的系统参数,该参数与路测数据中所使用参数保持一致。
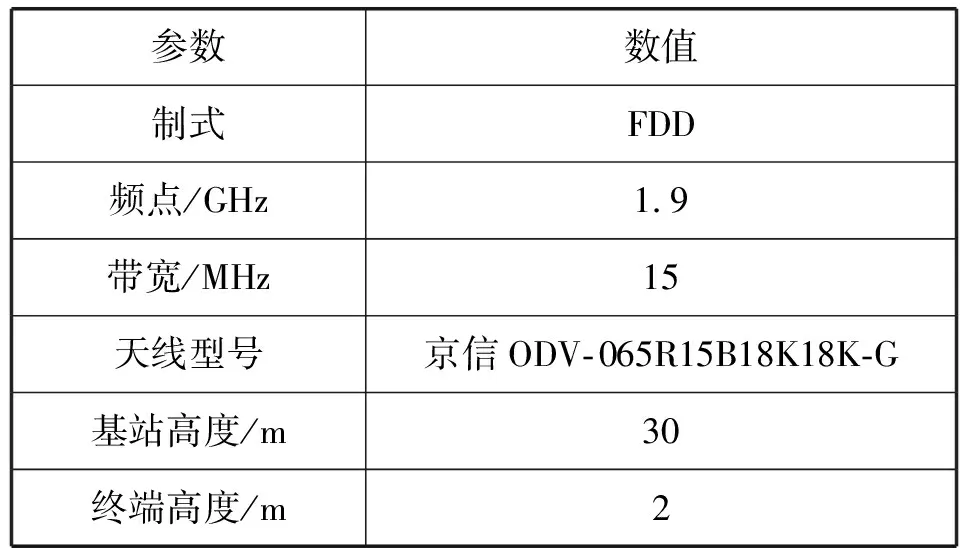
表1 仿真参数
仿真中遗传算法参数:种群规模M取值20,交叉概率Pc取值0.8,采用轮盘赌的选择策略,最大代数取值1 000,停滞代数为50,估计参数搜索范围[0,100]。
3.1 未分段SPM校准
SPM系数默认取值分别为k1=17.4,k2=44.9,k3=5.83,k4=0,k5=-6.55,k6=0,kclutter=1,f(clutter)=0,由于系数k1、k2分别代表传播模型的截距和斜率,SPM模型主要对k1、k2进行校准,在校正区域里得到一个唯一传播模型[5,8]。
使用基于奇异值分解的SPM校准算法可以得出表2中未分段SPM校准后的k1、k2值分别为86.19和22.70;由遗传算法可以得出校准后的k1、k2值分别为76.87和26.73。
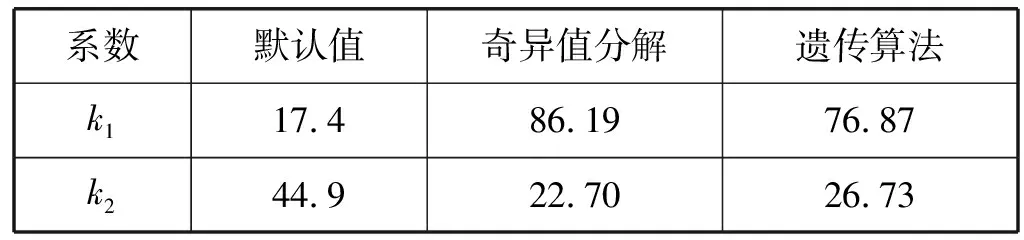
表2 未分段SPM系数比较
图3给出了SPM校准前,基于奇异值分解的SPM校准,以及基于遗传算法的SPM校准与测试数据的仿真对比。

图3 SPM校准对比(未分段)
可以看出,校准前SPM与实测数据相差甚远,通过奇异值分解和遗传算法对SPM校准后,与实测数据在距离小于500 m时比较接近,与测试数据中值线吻合较好,但距离大于500 m时仍有一定的误差。
表3对未分段SPM的校准误差进行整体分析,从统计结果可以看出,基于奇异值分解的SPM校准相比校准前,误差均值由-18.54下降到0,标准差由10.86 dB下降到7.92 dB,符合校准标准。基于遗传算法的SPM校准误差略高于奇异值分解,但仍远优于默认值。
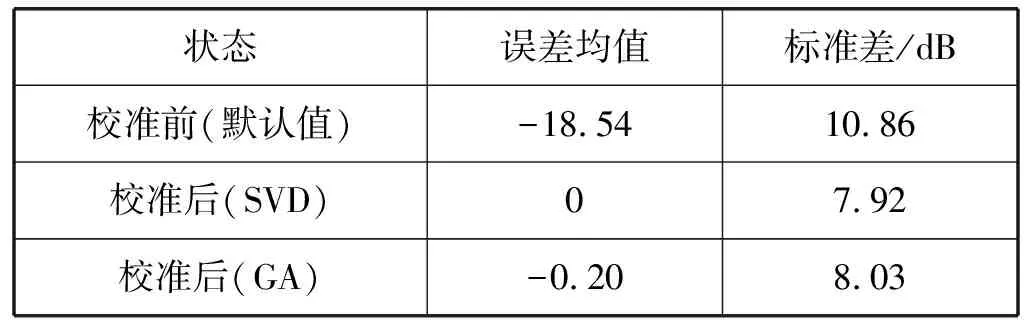
表3 未分段SPM的校准误差分析(整体统计)
为了更准确分析每一段的校准效果,因此通过表4对校准误差进行分段统计。
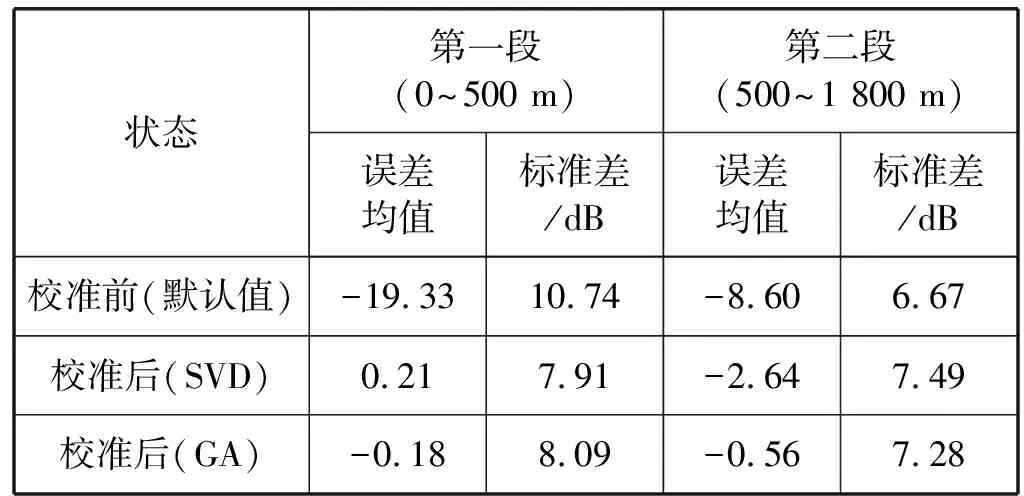
表4 未分段SPM的校准误差分析(分段统计)
可以看出,基于奇异值分解和遗传算法的SPM校准与未校准前的默认值和实测值相比误差均值下降很多。同时,采用奇异值分解和遗传算法的SPM校准,第二段校准后的误差均值大于第一段。这与图3也比较吻合。
从分段统计来看,使用未分段的标准传播模型、奇异值分解和遗传算法,虽相比默认系数起到一定的校准效果,但均未达到校准标准,因此本文提出基于中值线的分段标准传播模型。
3.2 分段SPM校准
根据分段SPM校准流程,首先描绘出测试数据的中值线,如图4所示,然后确定分段点p0为500 m。最后再按照分段点对每一段测试数据,基于奇异值分解或遗传算法进行校准。
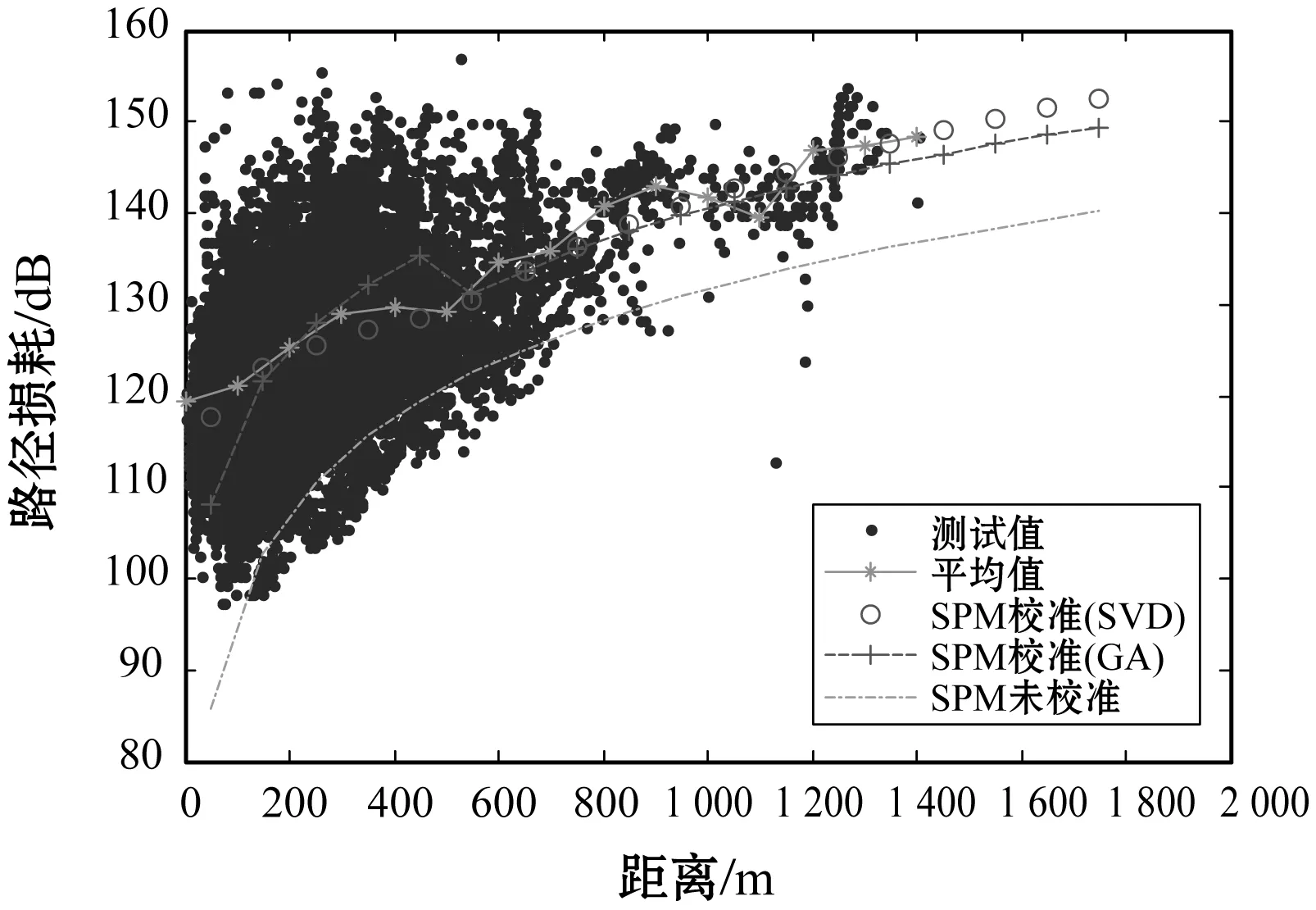
图4 分段SPM校准对比
表5为通过奇异值分解和遗传算法对分段SPM每一段分别进行校准,得到的k值系数。
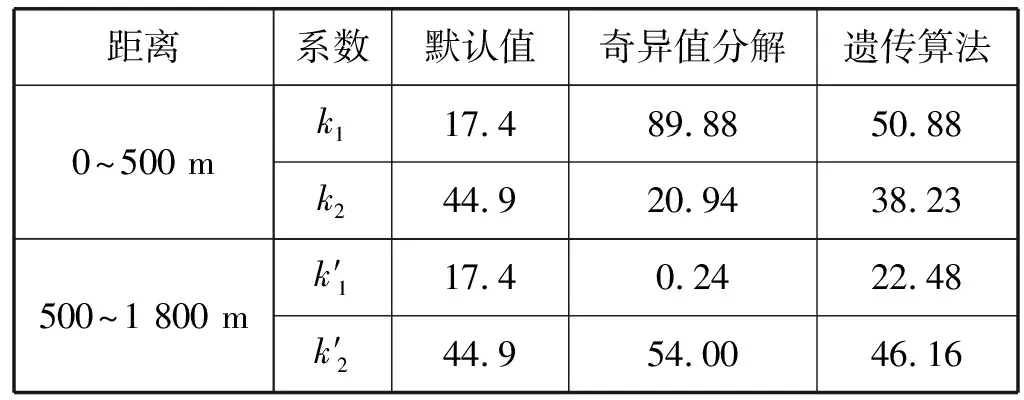
表5 分段SPM的校准系数比较
图4为分段SPM校准效果对比图,可以看出,通过分段校准,基于奇异值分解校准算法得到的传播模型与测试数据中值线可以很好地吻合。遗传算法得到的传播模型在距离大于500 m时也可以达到较好的校准效果,距离小于500 m时校准效果略差些。
表6为分段SPM校准误差整体统计分析,从统计结果可以看出,基于奇异值分解的校准算法,由于得到的是最小范数最小二乘解,因此校准效果最优,校准误差均值为0,标准差为7.8 dB,符合校准标准。由于基于遗传算法的校准得到的是局部最优解,校准效果相比奇异值分解的方法略微下降。
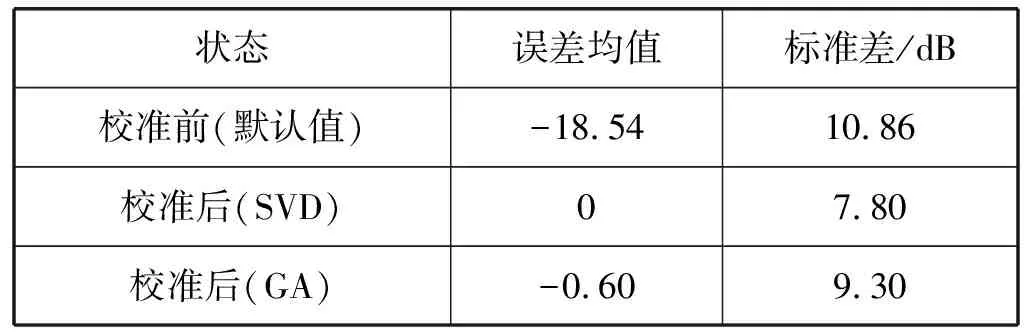
表6 分段SPM的校准误差分析(整体统计)
对于分段SPM校准误差的分段分析,从表7可以看出,采用遗传算法的SPM校准,第二段校准误差相比第一段较小,与图4所示吻合。基于奇异值分解的校准方法,对两段测试数据都达到很好的校准效果,误差均值均为0,标准差分别为7.89 dB和6.58 dB,符合校准标准。
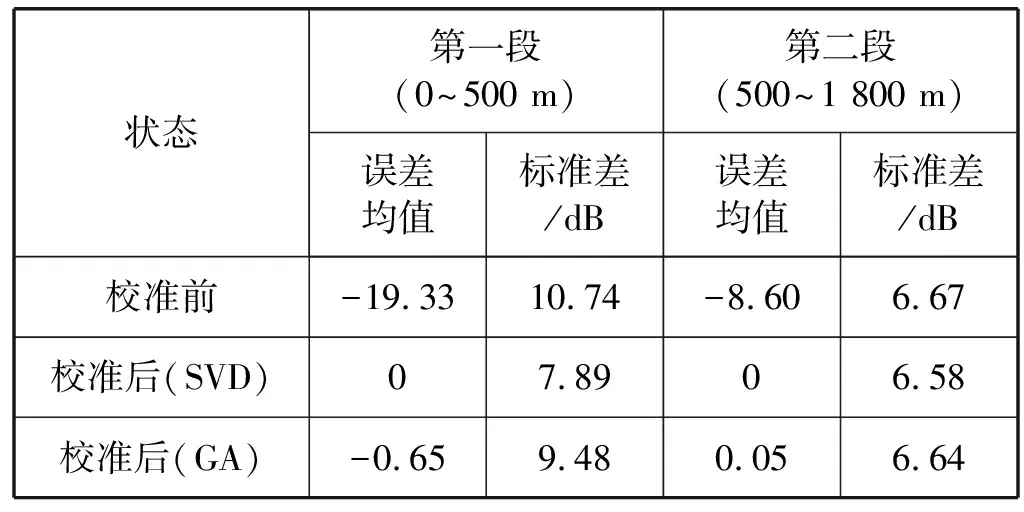
表7 分段SPM的校准误差分析(分段统计)
从表7和表4的对比分析可以看出,所提分段标准传播模型相比未分段SPM、使用奇异值分解的方法,可以达到更好的校准效果。
3.3 复杂度分析
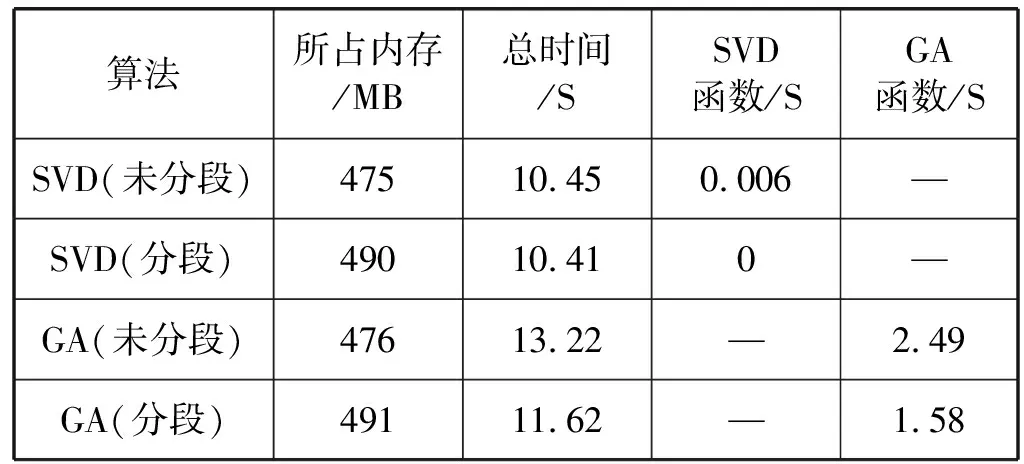
奇异值分解一般分两步进行。首先,将一个M行N列矩阵变换成一个双对角矩阵,若M>N,这个过程的计算量是O(MN2),若M 遗传算法本质上是二维搜索,寻找局部最优解。因此,若遗传算法种群规模为P,遗传算法的终止进化代数为G,则计算复杂度为O′(PG)。 表8给出了不同校准方法下理论上复杂度对比。未分段SPM奇异值分解算法的系数矩阵A大小为15 885×2,因此复杂度为O(15 885×22)。分段SPM奇异值分解算法分为2段,第一段系数矩阵A大小为14 704×2,第二段系数矩阵A大小为1 181×2,可知复杂度为O(14 704×22)+O(1 181×22)。未分段SPM遗传算法中,种群规模20,收敛代数为611,因此复杂度为O′(20×611),分段SPM遗传算法第一段和第二段收敛代数分别为308和130,因此复杂度为O′(20×308)+O′(20×130)。 表8 不同校准方法复杂度比较(理论) 仿真中,计算机配置为CPU Intel®CoreTMi5- 4210U CPU @1.7 GHz;内存:12 GB DDR3。表9是该配置下计算机实际仿真中复杂度的比较。 表9 不同校准方法复杂度比较(仿真) 可以看出,分段SPM校准方法与未分段相比,由于内存中变量有所增加,因此占用内存空间略有增加。分段奇异值分解算法相较未分段奇异值分解算法,内存由475 MB增加到490 MB;分段遗传算法相较未分段遗传算法,内存由476 MB增加到491 MB。分段SPM校准算法与未分段相比,即使仿真次数线性增加,但是由于每段数据量会相应减少,这会导致每次仿真时间指数下降,最终仿真时间也会下降。分段奇异值分解算法相较未分段奇异值分解算法,仿真总时间由10.45 s下降到10.41 s,其中执行奇异值分解函数的时间由0.006 s,下降到可忽略不计;分段遗传算法相较未分段遗传算法,仿真总时间由13.22 s下降到11.62 s,其中执行奇异值分解函数的时间由2.49 s,下降到1.58 s。 本文提出一种基于中值线的分段传播模型,同时提出基于奇异值分解和遗传算法的最小二乘传播模型校准方法。从仿真结果可以看出,使用所提分段传播模型,相对于未分段传播模型,可以达到更好的校准效果。由于奇异值分解的校准算法具有最小范数最小二乘解,而遗传算法通过二维搜索得到局部最优解,因此奇异值分解算法的校准准确度优于遗传算法,这也与分段传播模型校准仿真给出的误差统计分析结果相吻合。本文所提基于中值线的分段传播模型使用奇异值分解的校准方法的校准误差符合校准标准。 同时,从复杂度分析可以看出,使用分段传播模型校准的方法,虽然仿真校准次数有所增加,但每次校准的仿真数据量相应线性减少,这会导致每次校准复杂度的指数下降,因此,最终所需仿真时间也略有下降。并且,本文所用的奇异值分解和遗传算法,两种不同校准方法,可以扩展到多变量标准传播模型系数校准。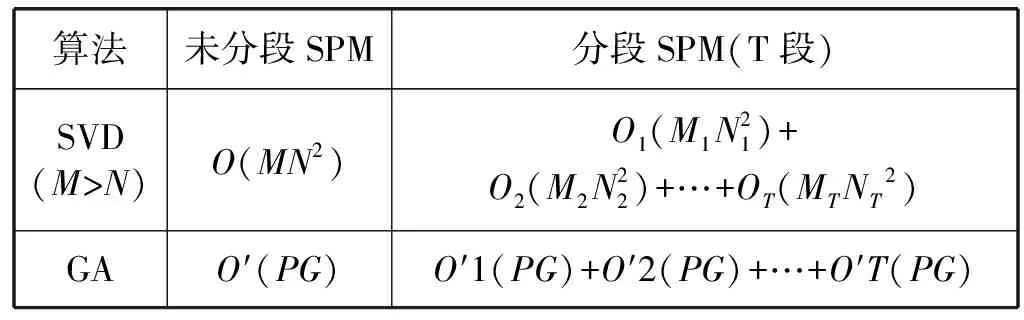
4 结 语
