面向压裂施工曲线的金字塔模型的构建方法

2022-12-03郑永果

计算机应用与软件 2022年11期

陈宁郑永果

(山东科技大学计算机科学与工程学院山东青岛 266590)

0 引言

压裂工艺是石油开采工艺中的重要组成部分，压裂施工曲线图是压裂过程的重要反映，也是压裂效果评价的重要依据[1]。根据曲线的特征可以监控作业施工、判定施工质量、分析施工情况[2]。压裂施工曲线图通常由三条曲线组成，是以时间为横坐标，以施工泵压、施工排量、砂浓度为纵坐标的曲线图[3]，但在实际作业中压裂施工曲线图包含多条压裂施工参数曲线。

金字塔模型是一种重要的数据组织形式和应用模型，众多学者对其已有广泛的研究并取得了重要的成果[4]。在遥感影像的应用中，金字塔模型的构建方法通常分为两种，一种是根据数据源本身存在的多种分辨率直接构建相应分辨率的金字塔模型，另一种是只有原始数据需利用重采样的方式建立不同分辨率的金字塔模型[5]。

根据压裂工艺中的压裂施工参数、数据采集频率和采集周期三个因素的综合考虑，将这些大数据量的曲线数据一次性全部加载并绘制出曲线不仅响应等待时间过长，而且消耗大量的内存。因此如何对海量压裂施工曲线数据进行有效的组织，使其具有高交互性是一个值得研究的问题。在保证曲线形状特征不变的前提下，结合Douglas-Peucker算法和金字塔缓存模型的构建思想，本文提出一种面向压裂施工曲线的金字塔模型的构建方法，并通过实验证明了该方法的可行性，实现了海量压裂施工曲线数据高效加载、快速绘制及浏览的性能。

1 曲线数据金字塔模型

金字塔模型在图像处理、图像压缩、图像检索方面有着广泛的应用[6]。本文中的曲线数据金字塔模型是在分析现有金字塔模型构建思想的基础上提出的一种面向压裂施工曲线数据的多数据量级别的层次模型。曲线数据金字塔模型是实现海量压裂施工曲线数据可视化的基础。

从曲线数据金字塔模型的顶层到底层，形成数据量按比例逐渐增大的多层次集合，越接近底层，所表示的曲线数据信息越详细，但每个层次所表示的曲线形状特征始终保持不变。如图1所示，曲线数据金字塔模型的底层数据量最多，顶层数据量最少，并且相邻两层的数据量为两倍关系。采用曲线数据金字塔模型存储压裂施工数据的优点是，当对压裂施工曲线数据进行显示时，能够快速显示数据量最少的顶层，随着缩放操作的进行，只需按照显示的需求选择最接近的层次进行显示，不需要读取整个数据集，减少了数据的I/O操作和网络间的数据传输，提高了曲线绘制效率及浏览速度。

图1 曲线数据金字塔模型

2 基于Douglas-Peucker算法的曲线数据金字塔模型构建算法

2.1 曲线特征点提取

曲线数据金字塔模型的构建过程中，采用曲线数据压缩算法按照曲线数据金字塔模型的层次，自底层逐层向上依次对原始数据进行压缩，以满足曲线数据金字塔模型各层对数据量的要求。曲线压缩对于计算机图形学、计算机制图学等有着重要的意义。曲线压缩也称为曲线特征点提取，是将曲线近似地表示为一系列点，安全地过滤曲线冗余数据点的方法，其实质是一个信息的压缩问题。从组成曲线的数据集合中抽取一个子集,该子集能够从内容上近似地反映原集合[7]。

本文中采用较为经典的Douglas-Peucker算法对压裂施工曲线数据进行压缩。Douglas-Peucker算法是通过保留关键点删除次要点来达到曲线数据压缩的目的[8]。该算法突出的优点是它不仅是一个整体算法，可以从整体上有效地保持曲线要素的形态特征，减少数据冗余，而且能够利用递归过程有效地完成算法实现[9-10]。Douglas-Peucker算法的步骤如下：

步骤1将曲线的首末两点P1、Pn虚连成一条直线。

步骤2计算曲线上除首末两端点的所有点Pi(i=2，3，…，n-1)与直线P1Pn距离d,选取距离最大的点PM和最大距离dM。

步骤3比较最大距离dM是否小于预先设定的阈值D，若是，则将曲线上的中间点全部舍去。

步骤4若否，则点PM为该曲线的特征点，并以该点PM为界，把曲线分为P1PM和PMPn两部分，分别对这两部分重复进行以上步骤，直至无法做进一步的压缩为止，算法结束[11]。

2.2 曲线数据金字塔的构建算法

压裂施工曲线图的绘制显示效果与绘制方法存在必然联系，不同的绘制方法对应的最优绘制点个数是不同的，当绘制点个数达到最优时，曲线绘制效率最佳。本文针对压裂施工曲线图的绘制特性，采用基于XML的SVG技术进行绘制。经多次实验得出，当绘制点个数为2 000时，即所有压裂施工参数构建的曲线数据金字塔型的顶层总数据量为2 000时，曲线绘制及浏览效率最优。

曲线数据金字塔模型的顶层数据量Mtop可由公式(1)计算得出：

曲线数据金字塔模型的最大分层数level，可根据曲线数据金字塔模型顶层的数据量Mtop以及该参数的原始数据量M来确定。level可由式(2)计算得出：

Mtop=M·2-level

(2)

曲线数据金字塔模型每一层的理想数据量Mideal，可根据最大分层数level以及该参数的原始数据量M来确定，Mideal可由式(3)和式(4)计算得出。

Mideal=M·2-k

(3)

式中：1≤k≤level。

Mideal=round(Mideal,-2)

(4)

曲线数据金字塔模型的构建流程如图2所示。

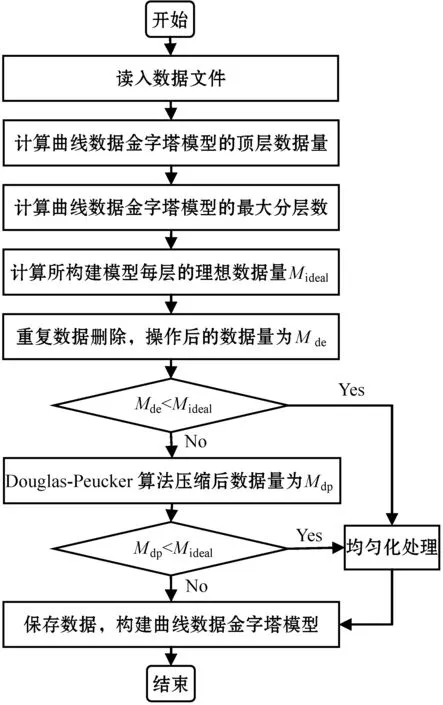
图2 曲线数据金字塔模型的构建流程

重复数据删除操作，即删除数据集中的重复数据，只保留其中的一份，从而消除冗余数据。重复数据删除操作后再应用曲线压缩算法对压裂施工曲线数据进行压缩，两种方法相结合，以提高数据的压缩效率。

在采用Douglas-Peucker算法对数据进行压缩时，压缩的结果与阈值的大小存在直接关系，压缩后的数据量随阈值的增大而减少。为了避免因固定阈值以及阈值选取的不确定性而导致压缩效率降低的情况，本文采用了一种自适应阈值的调节方法。阈值D的大小自动根据压缩后的数据量Mdp和理想数据量Mideal不断调整。自适应阈值D可由式(5)计算得出：

式中：D0表示初始阈值。

式中：Ymax、Ymin分别表示压裂施工参数的最大值与最小值。

在数据压缩的过程中，除了需要保证曲线形状特征不变，还需要考虑压缩后数据分布的均匀性以及压裂施工曲线数据展示的高交互性，因此采用了一种均匀化处理的方法。该均匀化处理方法是对压缩后曲线分布稀疏的间隔进行插值，增强压裂施工曲线图的可读性。本文在均匀化处理操作时，插值的数据将从原始数据中选取，以保证数据的真实性。

曲线数据金字塔模型的构建算法如下：

输入数据：压裂施工参数。

输出数据：压裂施工曲线图。

1. 初始化参数，将参数值转化为逻辑坐标值。

2. 通过式(1)计算每个压裂施工参数所构建的曲线数据金字塔模型的Mtop。

3. 对原始数据进行重复点删除，操作后数据量为Mde。

4. 通过式(1)的Mtop和式(2)计算曲线数据金字塔模型的分层数。

5.fori=1,2,…,leveldo

6. 依次通过式(3)和式(4)计算曲线数据金字塔的Mideal。

7. 依次通过式(5)和式(6)调整Douglas-Peucker算法中的阈值D进行曲线数据特征点提取。

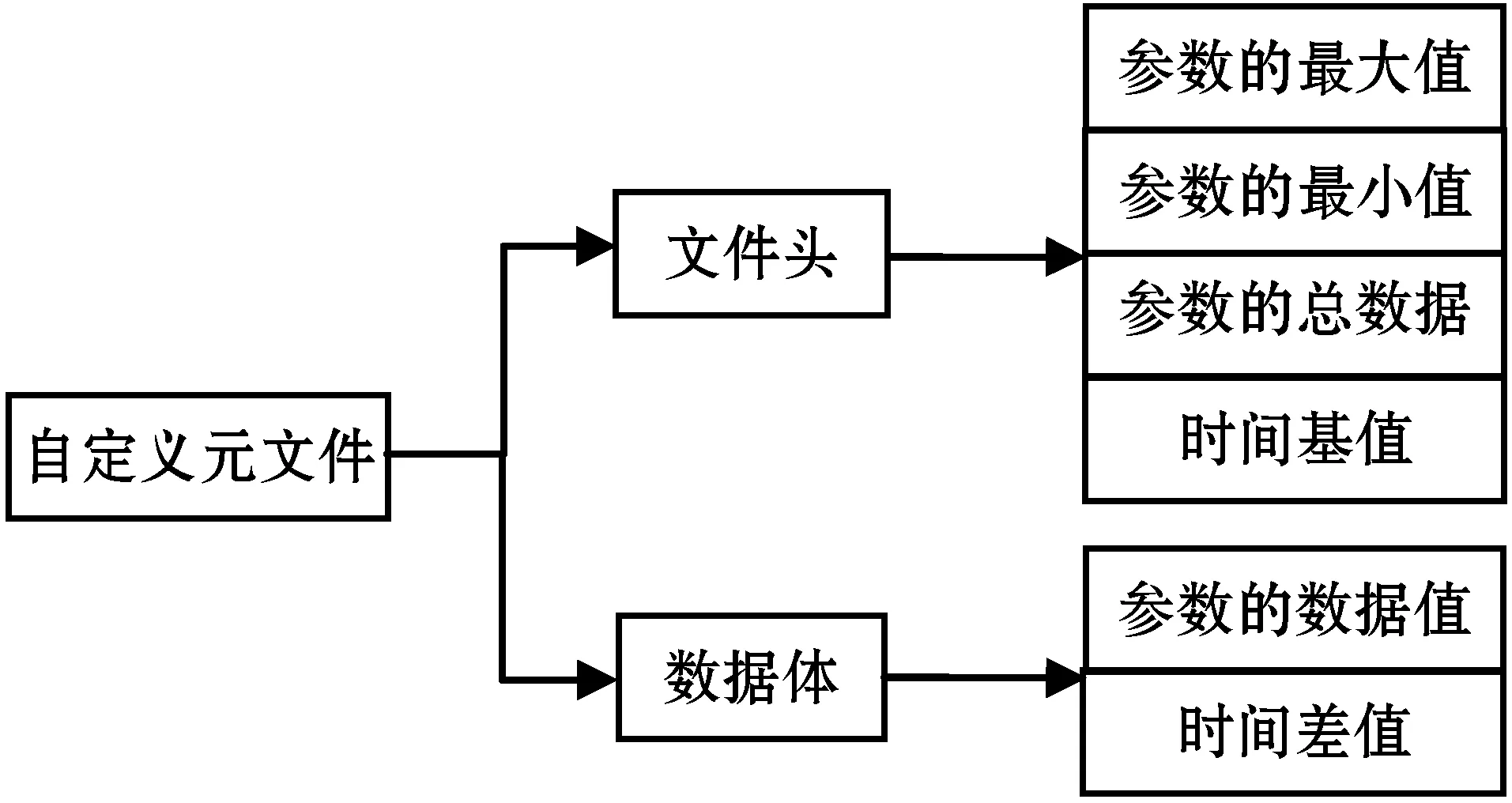
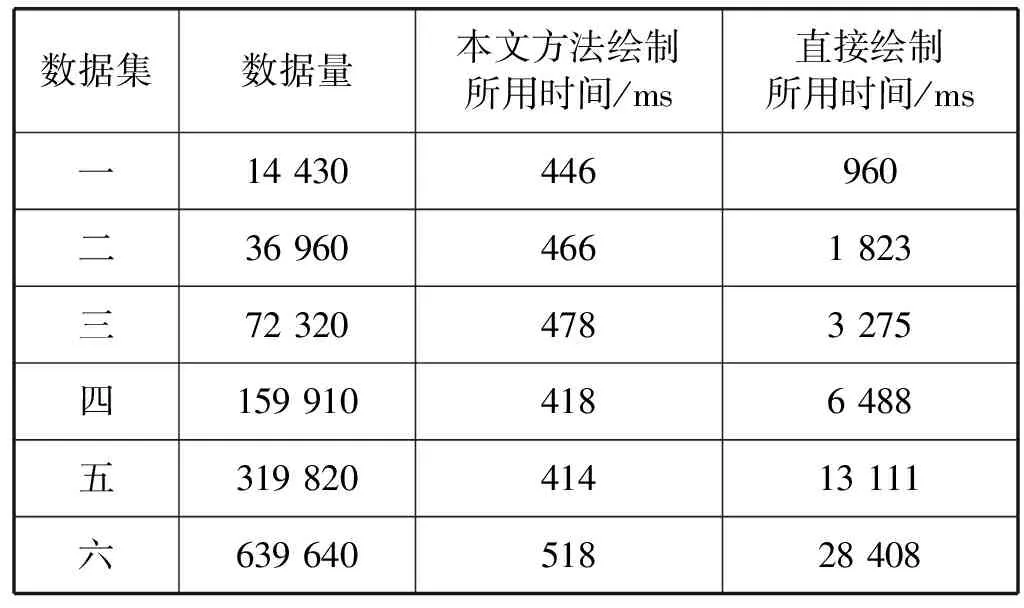
8.ifMdp

9. 均匀化处理。

10.endif

11.endfor

3 曲线数据金字塔的存储组织结构

压裂施工曲线数据的组织形式是数据存储过程中的重要环节，也是曲线数据金字塔模型构建的重要步骤。曲线数据金字塔模型的每个压裂施工参数的数据分别存储在单独的文件中，以参数名来命名。每个压裂施工参数所构建的曲线数据金字塔模型的每层数据分别存储在不同的自定义元文件中。这个自定义元文件由文件头和数据体构成。

该自定义元文件采用二进制形式进行存储，并添加信息头进行加密，确保数据的安全性。文件头记录压裂施工参数的最大值、最小值、总数据量、时间基值。时间基值指的是压裂施工的开始日期。数据体记录压裂施工参数的数据值以及时间差值。时间差值指的是每个压裂施工参数的施工日期与时间基值的差。为了便于曲线压缩算法中的计算，需要将数据集中的压裂施工日期全部转化为毫秒数。曲线数据金字塔数据的存储组织结构如图3所示。

图3 数据的存储组织结构

4 实验结果及分析

本文提出的曲线数据金字塔模型构建中，首先计算出该曲线数据金字塔模型的最大分层数，其次根据最大分层数从金字塔底层至顶层构建曲线数据金字塔模型。为了验证算法的可行性，测试曲线数据金字塔模型的数据处理效率，对本文方法和直接绘制的方法进行对比，得出了压裂施工曲线在数据量、绘制时间、缩放浏览性能的实验对比结果。

实验在64位Windows 7系统下，使用处理器为Intel(R)Core(TM)i3-2120M、内存为4 GB的计算机，在360浏览器的极速模式下进行测试。实验数据为某油田一号井的10个压裂施工参数的数据信息，实验结果如表1所示。

表1 实验结果

通过实验结果表明，当数据量较少时，采用本文方法与直接绘制的方法在绘制时间上差别较小，浏览效果流畅；随着数据量的增大，采用本文方法与直接绘制的方法在绘制时间上差别较大，本文方法在对大数据量的曲线数据进行绘制显示时更加快速，而直接绘制的方法响应等待时间长，甚至在处理大数据量的数据时会导致浏览器崩溃。因此本文提出的曲线数据金字塔模型在曲线数据的处理、绘制方面更加快速、高效，而且不受数据量大小的影响，实现了压裂施工曲线图加载、浏览的快速响应。