一种适用于大交通流量的路口通行方案

张 永 李凤坤

(大连东软信息学院 辽宁 大连 116023)

0 引 言

路口位于道路相交处，是各个方向道路的共享区域，属于“关键资源”。路口管理对道路网络的通行效率有非常重要的作用。路口通行方案是指协调路口各个交通流有序、高效地通过路口的方法、策略等，换句话说，是对“关键资源”实现有效管理的策略。

分析现有文献，路口通行方案大体上可以分为两大类[1-2]：固定式(Static or Fixed-time Control)，激励式(Actuated Control)或自适应式(Adaptive Control)。固定式规划方法通过统计的方式制定一个信号切换的顺序和各色信号的时长。这种方法不考虑路口不同时段交通状况的变化，都统一使用一种固定的顺序和信号时长。学术界普遍认为该方法存在局限性。激励式或自适应式方案主张根据交通流的实时情况计算各个方向信号的顺序或时长。例如，文献[1]根据传感器获取的路口的实时数据，包括交通流量、平均等待时间、空闲情况、特殊情况、相邻路口的影响等，设计了信号顺序和时长计算方法。文献[3]通过收集路口车辆的速度数据，综合计算来调整交通灯的时间，实现实时的交通灯控制。类似的还有文献[4-6]。

进一步分析发现，现有文献对路口实时交通数据和交通事件对通行方案的影响讨论较多[7-10]。对于各个方向交通流的内在关系及其对通行方案的影响讨论较少。

交通信号虽然是交通管理所必需的，但是，每引入一次信号切换都会带来一定的时间开销，从而减少了真正通行的时间。极端情况下，如果信号不断地变化，各个交通流根本无法通行，全是信号切换带来的开销；相反地，如果信号不变化，只能某一个交通流通行，则全是通行时间。分析交通信号之间的关系，据此设置科学的切换顺序，合理地管理信号切换，减少信号切换带来的开销，是对现有的方案的有益补充。本文据此思路开展研究。

本文首先分析了各交通流之间的关系，给出了并行关系、冲突关系、并行集、冲突集等概念，并分析了它们之间的关系，给出了定量描述。然后，提出包式交通流方案。该方案通过优化信号之间的切换顺序，在各交通流总通行时间相等的前提下，减少了信号的切换次数，降低了切换带来的时间开销，提高了通行效率。

1 包式交通流

为了准确描述通行方案，下面先引入几个相关的概念。

交通流(Traffic Flow,TF)是指汽车在道路上连续行驶形成的车流。使用符号fi表示，下标是标号。交通流有前进方向和轨迹两个属性。道路上的交通流轨迹没有相交点，不需要管理。在路口处，存在交通流交汇的地方，因此需要控制管理。如无特殊说明，下文中所说的交通流都是指路口处的交通流(或者说，交通流在路口处的部分)。本文以普通的四车道“十字型”路口为研究对象，该类型路口共存在8个交通流，如图1所示。

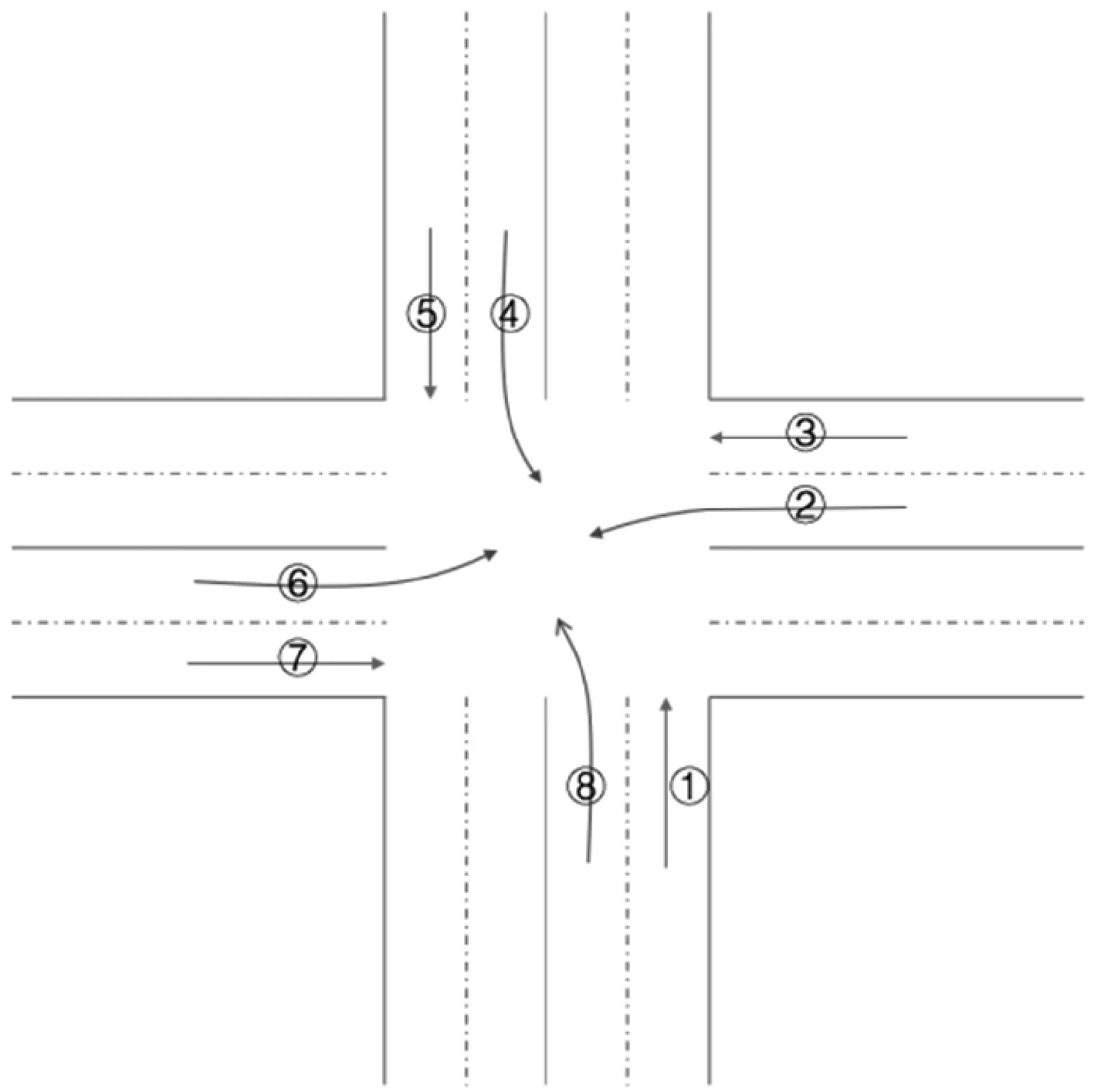
图1 普通四车道“十字型”路口交通流

交通流之间有冲突关系、并行关系，具体定义如下：

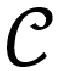
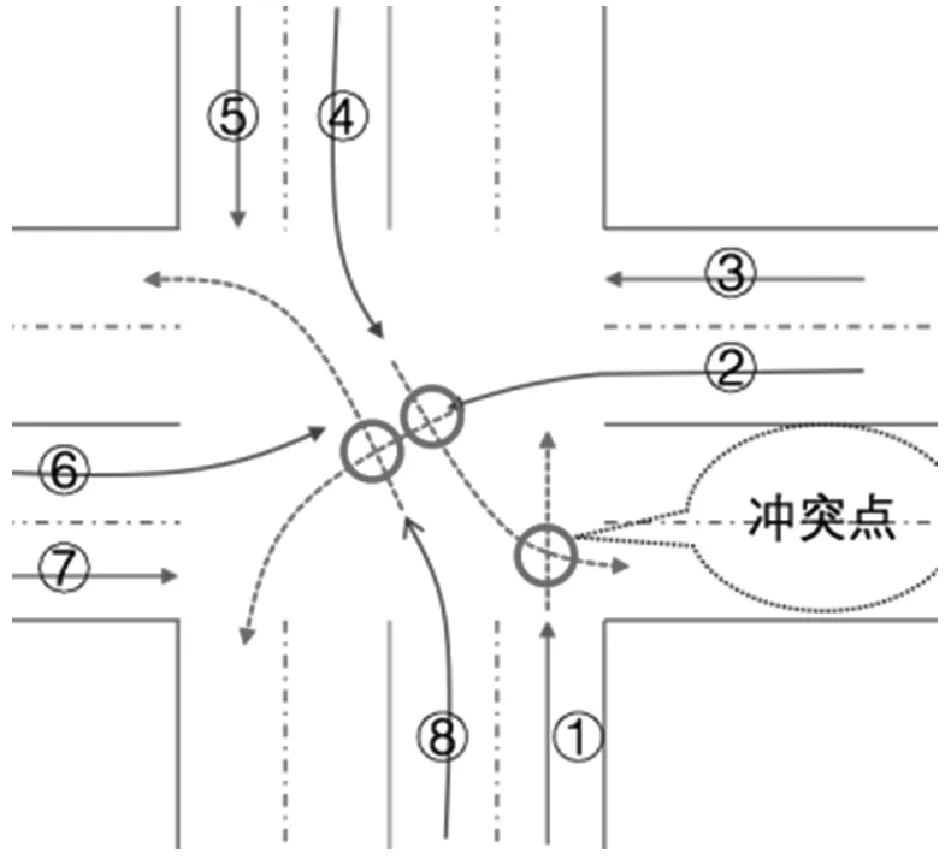
图2 冲突关系示意图

此外，在图1中，交通流f1与f4、f2与f4等也是冲突关系。

定义2并行关系(Parallel Relationship)，是指在某个参考区域中，轨迹没有交叉的交通流之间的关系，如图3所示。并行关系记为fx≃fy。fx≃fy等价于fy≃fx。

此外，图1中交通流f1与f8、f4与f8等也都是并行关系。

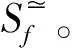
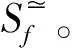
研究图1所示的路口可得出如下定理。

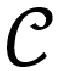
证明：

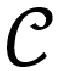
∴ 在并行关系分析上，实质上不同的交通流有两个，例如，f7和f0，其他的交通流都可以类似地分析。

∴ 以f7和f0为例进行证明。

先分析f0：

如图1所示，并据并行关系的定义，可知，f0分别与f4、f5和f7在轨迹上没有交叉。

同样地，f7分别与f0、f2和f3在轨迹上没有交叉。

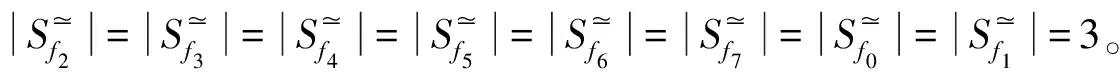
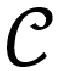
证毕。

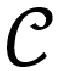
证明：与定理1的证明相同，实质上不同的交通流只有两个，还是以f7和f0两个交通流为例进行分析。

先分析f0：

由图1及冲突关系的定义可知，f0分别与f1、f2、f3和f6在轨迹上都有交叉。

同样地，f7分别与f1、f4、f5和f6在轨迹上都有交叉。

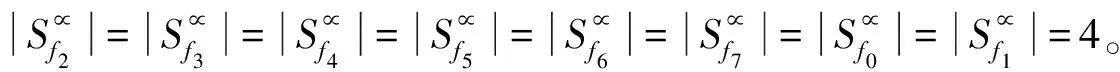
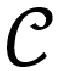
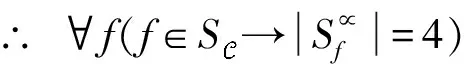
证毕。

如果按照如图1所示的方式对交通流进行依次编码，可以得出式(3)、式(4)和式(5)，用来计算一个交通流的并行集。

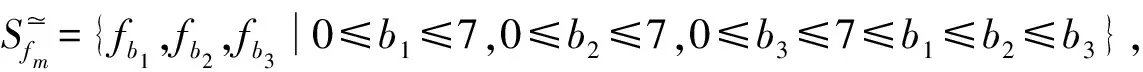
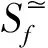
2 包式交通流通行方案

交通流控制最终形成交通信号灯的变化顺序。包式交通流通行方案本质上在于找到一条信号变化的路径，也就是包含了全部8条交通流作为主流包的循环单元，即满足式(6)所示的交通流循环。其中，当i=7时，(i+1)对8取模，即：(i+1)%8=0，进入下一循环或信号周期。c1、c2和c3三个条件同时成立，缺一不可。根据定理1和定理2，任何一个交通流的并行集都为3，冲突集都为4，也就是必定存在3个可以并行的次流，存在4个冲突的交通流。因此，可得到式(6)。

式(6)是选择条件，不是计算条件。也就是满足条件的循环需要通过遍历事先找到。下面以x0=f0为一个循环单位的起点为例说明式(6)的用法。同时，展示了满足式(6)的主流包循环的样子。

演示开始：

由前述我们知道：

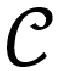
由c1条件,我们选择x0=f0。

由c2条件，可知：x1=f4,f5或f7。

∴ 下一个主流包应为Pf4、Pf5或Pf7，从而产生三个分支。

同理，应用一次c2条件，可得到下一个可能的主流包集合，产生相应的分支。

再由c3条件可知，在一个循环单元中主流包不能重复。即c3是删除重复分支的条件。

∴ 反复应用c2和c3条件，可得到一个树型结构。图4展示的是当x1=f4时的一个子树。x1等于f5或f7时，可以得到类似的树型结构。

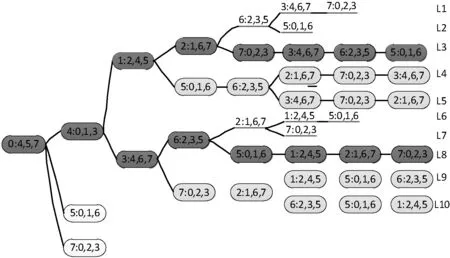
图4 并行流链路

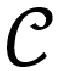
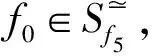
同样地验证L5、L8、L9和L10，只有L8是真的循环单元。

∴x1=f4子树，合法的循环单元为：

同样的方法，可得到x1=f5和f7时的合法循环单元。

演示结束。

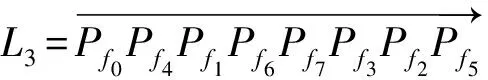
图5 L3循环单元的信号时序

图5中，纵轴是信号灯编号，横轴是时间。信号灯编号与图1中的交通流的编号相同。采用的是有向信号灯。例如，Pf0主流包的信号配置如图6所示。注意：图6中f4、f5和f7的绿灯是分时段顺次开启的，具体的顺序请参照图5中0T至3T时间段。

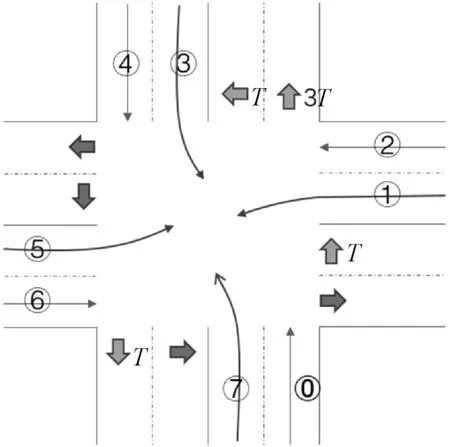
图6 主流包Pf0的信号配置

3 分析与评价

包式交通流通行方案的优势在于将通行周期内的分散的通行时间聚集起来，在通行机会均等的条件下，通过减少引入信号变换后带来的通行开销来达到提高通行量的目的。分析如下。

文献[11]指出图1所示的8个交通流共存在12种安全通行的组合方式，也就是并行集，分别是<0,7>,<1,2>,<3,4>,<5,6>,<2,6>,<0,4>,<1,5>,<3,7>,<3,6>,<0,5>,<1,4>,<2,7>。

实际上，任何通行方案最终都体现为对这12种组合方式的优化与控制。例如，现实生活中，最常见的信号顺序是沿着顺时针或逆时针的顺序来组织的。图7所示是逆时针顺序组织信号的时序。再如，文献[11]设计两个算法，能够利用无线传感器网络采集的数据来规划12种组合方式的切换顺序。

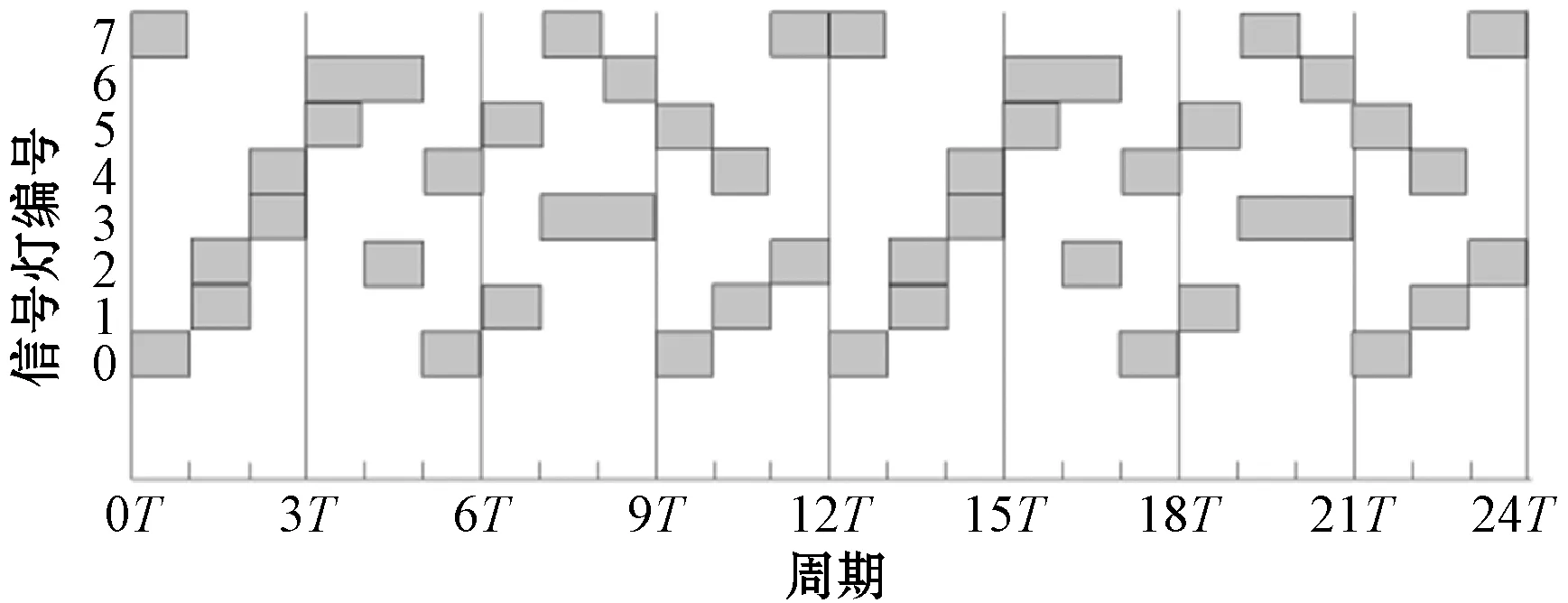
图7 12种组合逆时针切换时序

下面我们将包式通行方案信号时序与12种组合方式的时序进行比较。优化的时序如图8所示。

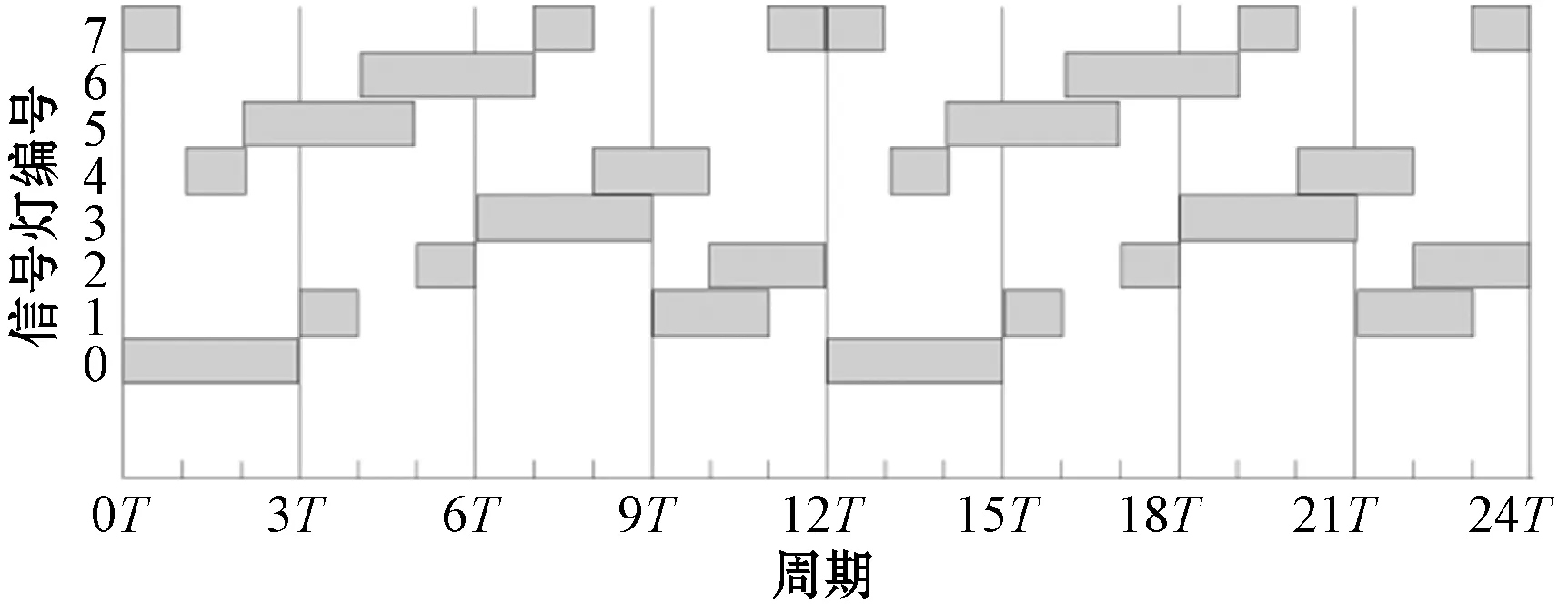
图8 优化的12种组合逆时针切换时序

对比图5、图7与图8的时序，可以得到表1的参数。通过表1，可以清楚地看出，在同样的48T时间内、同样的通行机会(每个交通流6次通行机会，即6个绿灯)情况下，包式通行方案最大连续通行时间为5T，占比为40/48，而其他方案最大为3T，最大仅为24/48。所以，得出结论：在同样时长、同样通行机会下，包式通行方案的连续通行参数最好。

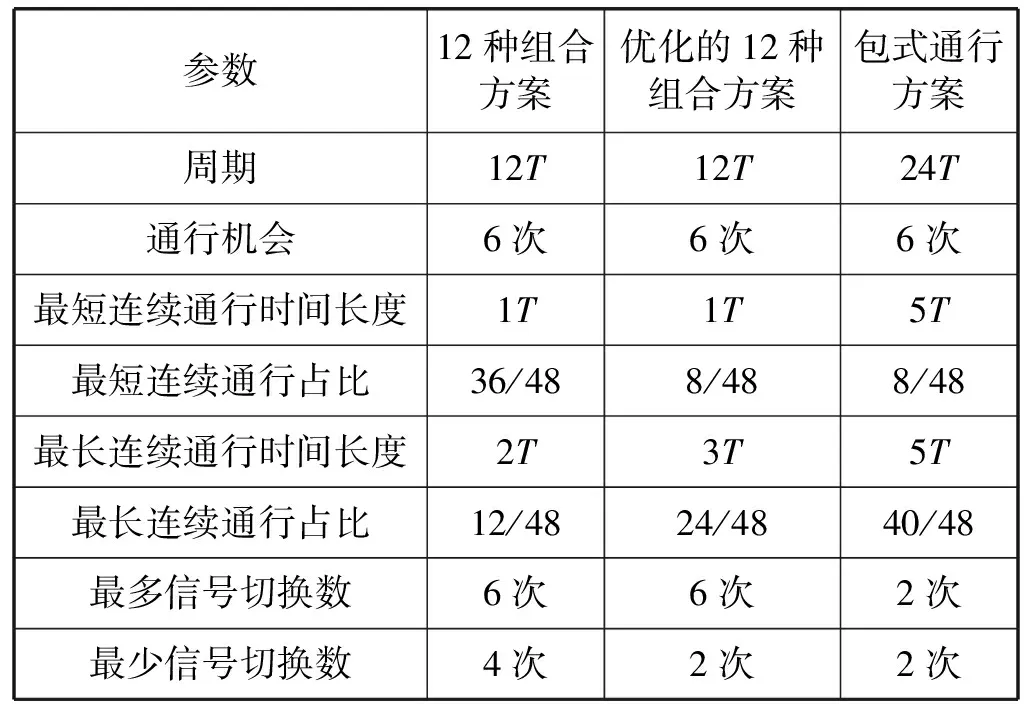
表1 24个通行单位方案参数对比

通过前面的分析，得出包式通行方案的连续通行参数最好。那么，这个优势对于交通流到底有什么好的作用呢？下面通过Vissim仿真数据来分析。

仿真软件为Vissim 5.20。使用的参数如表2所示。信号时序的实现如图9所示。信号周期为480 s，每个切换单位为20 s。采用包式交通流方案时，最长的通行时间为97 s。使用道路网如图10所示，采用中线(Center Line)显示模式。

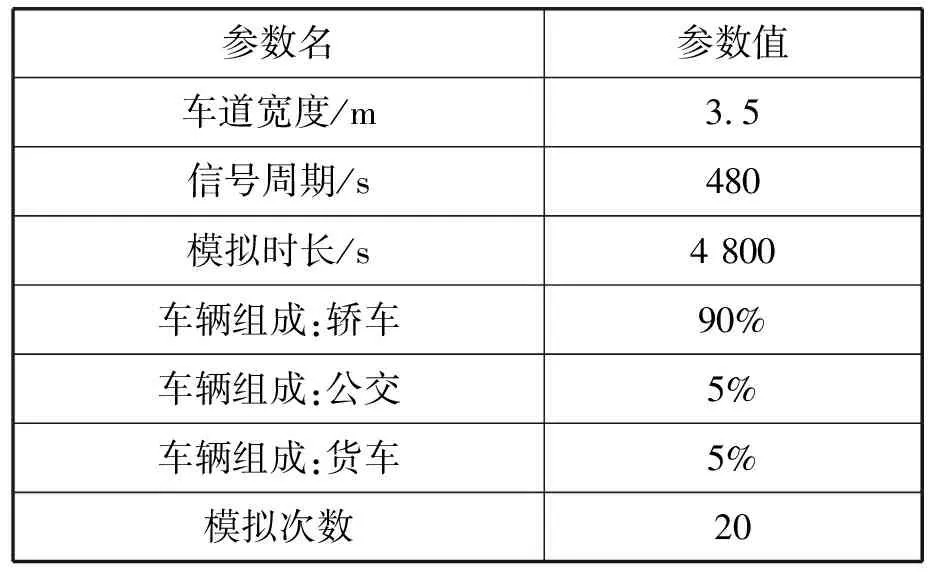
表2 仿真参数

图9 L3循环单元的信号时序在Vissim中的实现

除了表2写明的参数设置外，模拟的其他设置还有：

(1) 道路网没有合用车道，即直行与左转车道是分开的。

(2) 道路网采用单链路(Link)单车道的方式构建。

(3) 道路网要保证对向的左转车道不相交。如图10中的a与b所示，a与b互相为对向的左转车道，它们不相交。同理，c与d也不相交。

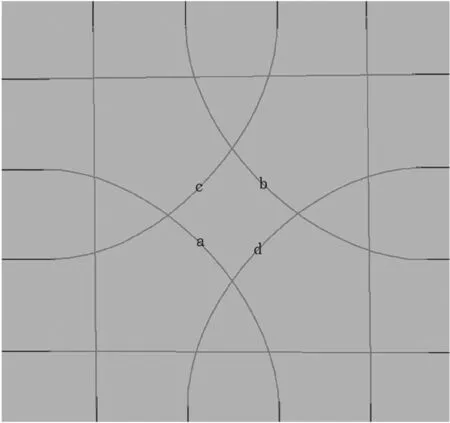
图10 模拟所用“十字”路口道路网(中线模式，center line view)

车辆输入密度为3 600时，三种通行方案所测值如图11所示。可以看出，三种方案在车速为40 km/s以下时，通过路口车辆大体相等，因此三种方案的性能基本一致；车速大于40 km/s时(也就是在道路限速比较高的情况下)，包式通行方案的优势开始显现。优化的12种组合方案性能次之，随机的12种组合方案性能最差。进行数据计算可知，包式交通流通行方案与普通的12种组合随机排序的方案相比，通行量提高约14.29%，比优化后的12种组合方案提高约8.47%。

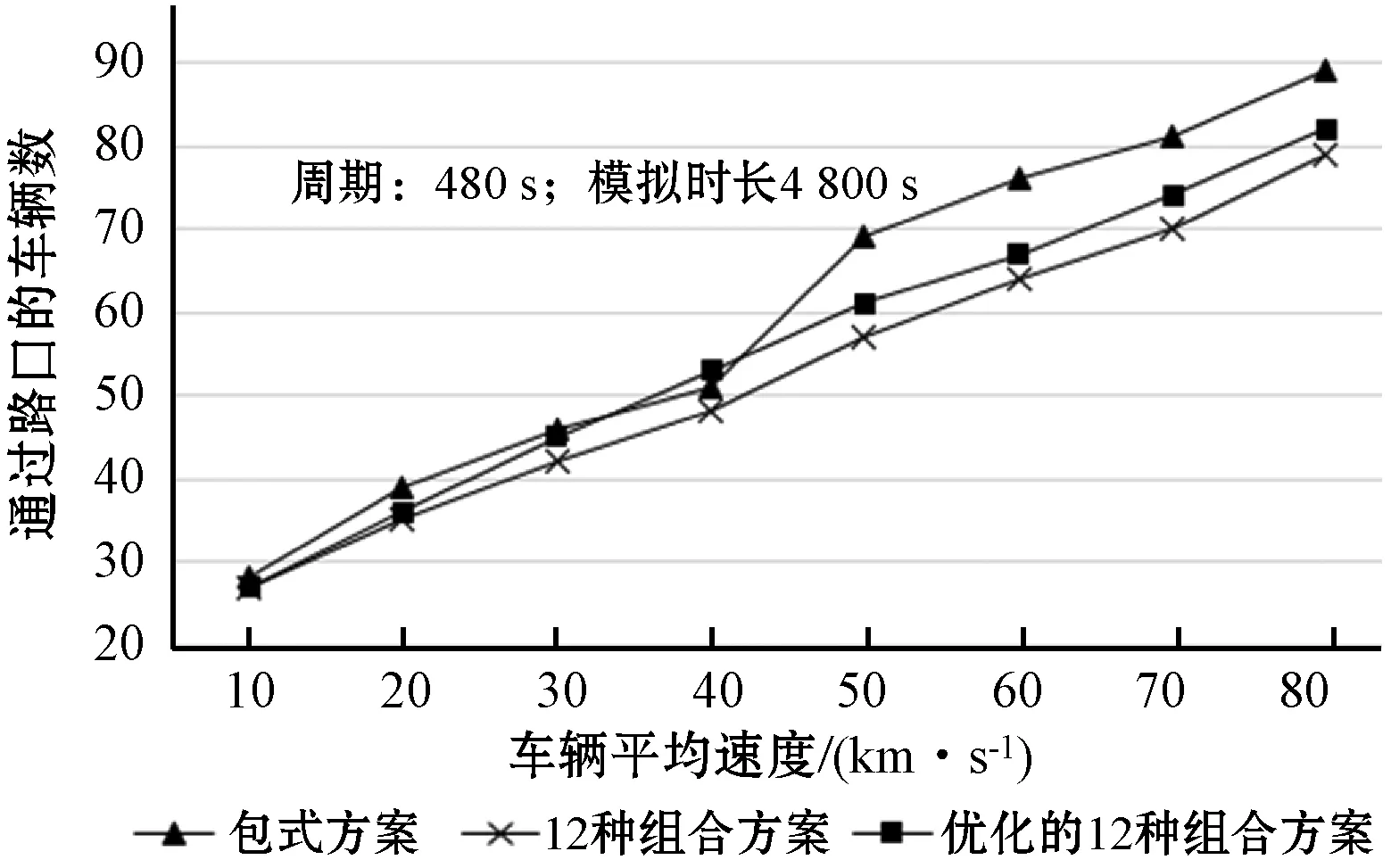
图11 车辆输入为3 600时，车辆通过路口的数量

车辆输入密度为1 000时，三种通行方案所测值如图12所示。三种方案在不同的车速时都基本一致。

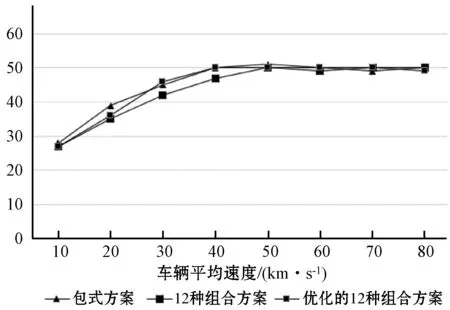
图12 车辆输入为1 000时，车辆通过路口的数量

对比图11与图12可以看出，在车速大于40 km/s时，之所以没有出现更大的车辆通行量，是因为车辆输入密度不够大，也就是路面上没有足够多的车。因此，限制了包式通行方案优势发挥。

综合分析图11和图12，能够得出结论：在车辆输入密度比较大时，包式通行方案有比较好的性能。

正如前面所分析的，包式通行方案具有较好性能的主要原因是在一个信号周期内，减少了信号切换的次数。在模拟器中，主流包Pf4通行周期内，其子流依次切换，如图13所示。

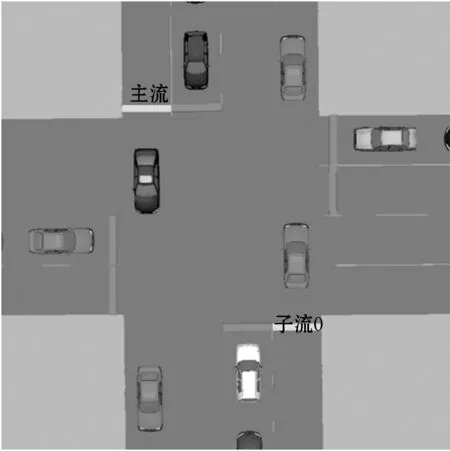
(a) 子流f0通行

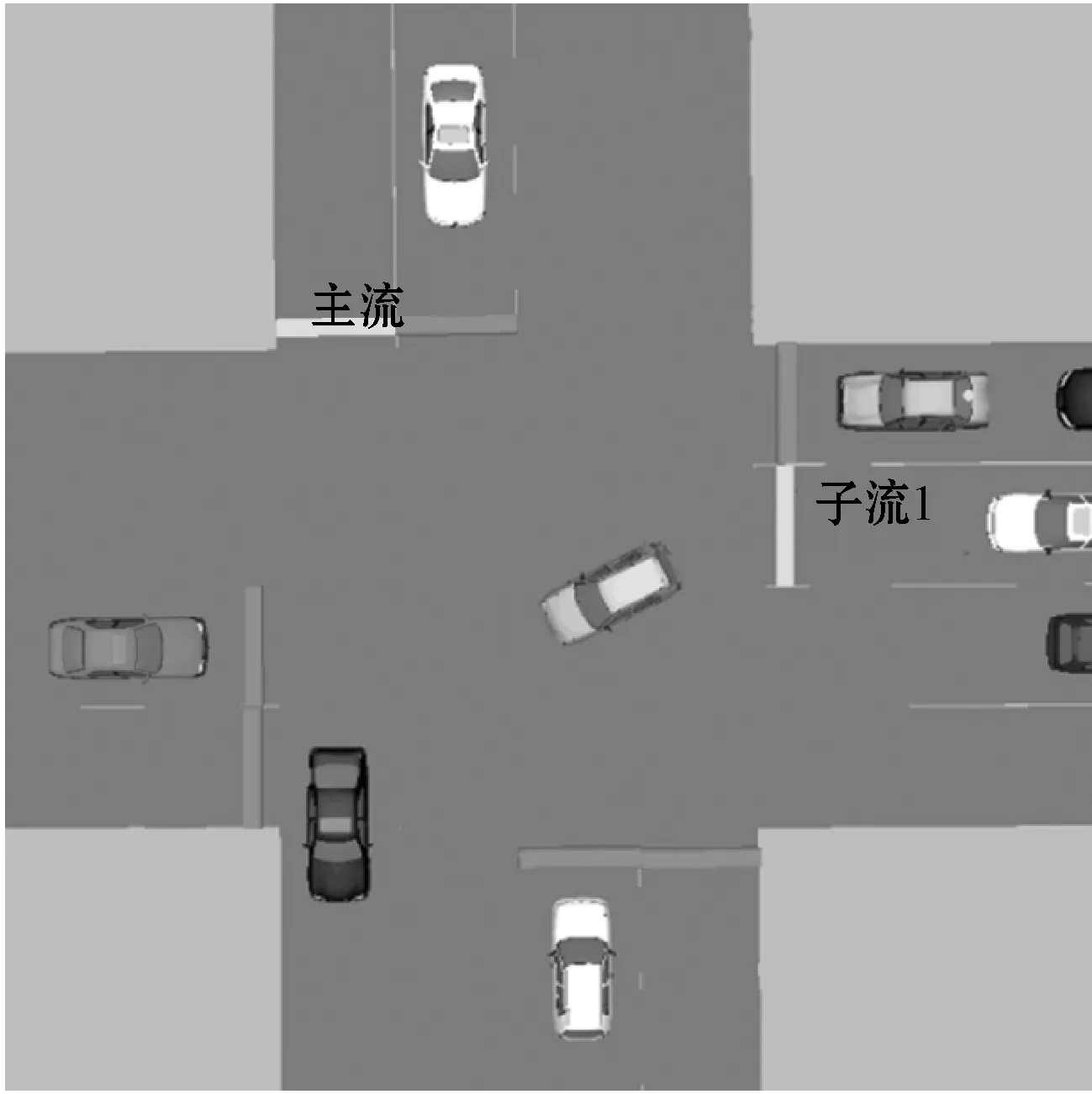
(b) 子流f1通行

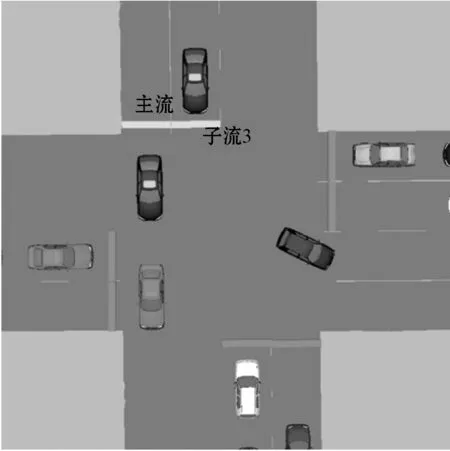
(c) 子流f3通行图13 主流包Pf4中子流切换模拟图

4 结 语

对于一个交通流而言，交通信号变为红色，会导致车流停止、等待，而信号恢复后车流有一个加速到最高限速的加速过程。即使刨除车流等待的时间(因为这段等待的时间内，其他车流在行驶，对于路口整体而言不是损失)，与没有该信号灯相比，该车流的通行量也会受到影响，直接原因是车流的减速与加速的过程也会导致通行量的损失。为此，本文提出并行、并行集等相关概念，推导了相关的定理，进而提出包式交通流通行方案。通过分析模拟实验数据证明了包式交通流通行方案在车辆输入密度比较大时，包式通行方案有比较好的性能，比普通的12种组合随机组合通行量提高14%。