对幂级数性质的分析研究
2022-12-03阳平华张清平
阳平华,张清平
(广州城市理工学院 计算机工程学院,广州 510800)
高等数学中幂级数内容对于学生来说难度较大,对幂级数性质的内在因素做了进一步探索,以期为教学带来一定的启示,提高教学质量。
1 幂级数概述
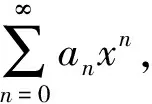
如果没有特殊声明,后面涉及的幂级数都为幂级数的标准形式。对幂级数的研究内容包括三方面:①幂级数在哪些点收敛,在哪些点发散,幂级数的收敛域及发散域;②求幂级数的和函数;③将函数展开为幂级数。
2 幂级数的性质
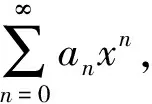
说明:①定理的证明跟正项级数的比较审敛法、比值审敛法有直接关系,所以说正项级数是基础;②定理表明:|x1|<|x2|,并且幂级数在区间(-|x1|,|x1|)收敛,在区间(-∞,-|x2|)和(|x2|,+∞)发散,在区间(-|x2|,|x1|)和(-|x1|,|x2|)的收敛性不确定(可画图直观了解),进一步结果需要发掘更多信息去加以研究;③收敛区间或收敛域的确定是基于Abel定理,收敛半径的求法是基于比值审敛法。
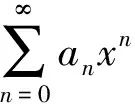
说明:①通常情况ρ≠0时可以直接写出R与ρ的数值关系,极端情况ρ=0或ρ=+∞时只能直接写出结果;②R的确定正是通过正项级数的比值审敛法得到的。
①幂级数的和函数s(x)在收敛区间(-R,R)内连续;②幂级数的和函数s(x)在收敛区间(-R,R)内可导,且对∀x∈(-R,R)有逐项求导公式:
③幂级数的和函数s(x)在收敛区间(-R,R)内可积,且对∀x∈(-R,R)有逐项积分公式:
定理3中①的内容是和函数的基本性质,②、③的内容是求和函数的理论基础。②、③概括来说就是“逐项求导,逐项积分”。
3 幂级数性质的基本应用
幂级数性质的应用主要介绍定理3,即“逐项求导,逐项积分”的一些应用,包括求一些幂级数的和函数及一些数项级数的和。
3.1 基本题型
对一些简单的幂级数,直接通过“逐项求导或逐项积分”对幂级数变形化简,再用已知幂级数的和函数。
上式两边同时从0到x(-1 上式两边同时对x(-1 3.2 深化题型 在教学中发现,学生对逐项求导比较习惯,对逐项积分比较生疏,而且逐项求导确实比用逐项积分用起来方便。实际上,通过分析发现“逐项求导,逐项积分”都只是表面现象。用逐项积分来解的题都可以用逐项求导来解,关键在于思考问题的角度。一般用“逐项求导,逐项积分”是相对和函数,即求和“∑”与求导或积分交换顺序,直观来说就是“由外向内”的运算,如果从通项开始“由内向外”交换运算顺序,就能避免用逐项积分,这样“逐项求导或逐项积分”就成为了“逐项求导”一种情况,只不过需要对和函数s(x)求导用“由外向内逐项求导”,需要对和函数s(x)积分用“由内向外逐项求导”,下面通过两个例子加以解析。如例2是用逐项积分求解的,也可以用逐项求导来求解,而且比较简练。幂级数求和函数也可以利用幂级数的性质结合微分方程求解的方法。 解: 解法一(逐项求导): 设: 设: 又: 解法二(逐项积分): 解法三(通过变量代换): 令x=z2z∈(-1,1) 解法一(结合一阶线性微分方程): 该级数缺偶次幂项,它的收敛域为 (-∞,+∞)。 设: 则: 于是有: 解此一阶线性微分方程,得: 又: 解法二(结合二阶线性微分方程): 原级数的收敛域为(-∞,+∞)。 设: 于是s″(x)=s(x)。该二阶方程的特征方程为r2-1=0,解得r1=-1,r2=1。 其通解为s(x)=C1e-x+C2ex。又s(0)=0,s′(0)=1,代入上式得: 故: 解法三(直接用展开式): 3.3 数项级数的和 对数项级数的研究应包括定性的和定量的两方面内容。定性的内容即是讨论级数的收敛性,定量的内容就是要求级数的和。在数项级数中求和的内容讲解的少即是暗示需要借助幂级数来求和。 所以: 阐述了Abel定理的内涵、幂级数收敛域的本质,发现了幂级数“逐项积分”和“逐项求导”的内在关系,对和函数求导是“由外向内逐项求导”,而对和函数积分是“由内向外逐项求导”,将较难处理的“逐项积分”法转化为较易掌握的“逐项求导”法,挖掘了幂级数求和函数与微分方程之间的关系,即幂级数求和函数的问题也可以利用幂级数的性质结合微分方程的求解方法。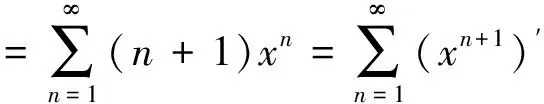
4 结语
