基于多尺度空间注意力的高精度数字全息散斑去噪方法

周孟航 赵自新 杨兴宇 杜怡君

(西安交通大学机械制造系统工程国家重点实验室，陕西 西安710049 )

0 引言

航空航天领域的安全性检测越来越重要，其中对叶片、机翼和芯片焊点等关键构件进行强度检测评估具有重要意义[1]。通过数字全息干涉术可以对这些构件的形貌形变进行无损、大范围、高精度的测量，进而评估构件的性能和强度。而这些构建的表面通常为光学粗糙表面，激光照射到这些表面上时，各个微小的粗糙面元的反射光会在空间中随机干涉，形成复杂的散斑噪声，利用这些散斑噪声的相关性可以对物体的面内形变应变等进行测量分析[2,3]，但是在数字全息测量的过程中散斑噪声会严重影响测量过程提取相位的质量，降低测量的精度。因此对降低散斑噪声带来的相位误差十分有必要。

散斑噪声是一种分布复杂的噪声，目前常见的降低散斑噪声干扰的方法有两种，一是从散斑的统计特性出发，获取多视角或随机照明的全息图，以平均的方式降低噪声的对比度。Quan, Chenggen等人通过改变不同的照明角度对散斑噪声进行平均[4]。此类方法通常是利用硬件进行实现，装置复杂，且需采集多幅全息图像，记录时间长。第二种方式是通过数字图像处理进行滤波。传统的图像滤波方法种类繁多，有中值滤波、均值滤波及小波变换等，其中基于BM3D框架的系列算法取得了非常好的去噪效果[5-7]。但是由于散斑噪声的乘性特点和分布不均匀特征使得图像中的信号和噪声难以像一般的高斯噪声那样分离，使得传统的数字滤波方法在数字全息散斑去噪的应用上很难取得很好的效果。

近年来，在大数据人工智能的热潮下，基于深度学习的图像滤波方法成为了研究的热点，基于卷积神经网络（CNN）的滤波方法不仅在自然图像领域取得了卓越的去噪性能[8-12]，也在光学计量领域展现了独特的优势。2019年，FUGUI HAO等人提出了一种基于卷积神经网络的分批去噪方法[13]，将一张电子散斑干涉条纹图分批下采样后一同输入网络进行去噪处理，获得了良好的去噪效果。2020年，Ketao Yan等人提出了一种两帧的神经网络去噪方法，将带有散斑噪声的正弦和余弦的干涉条纹一同输入网络，分别去噪后再计算得到滤波后的相位信息[14]。2021年，JIANMING LI等人提出了一种结合空洞卷积的散斑干涉条纹去噪方法，增加了对不同尺度特征的提取能力[15]。2022年，Javier Gurrola-Ramos等人提出了一种基于U-Net的条纹去噪网络，通过网络模型对噪声分布进行建模，进而去除噪声[16]。这些方法大多是对条纹图进行去噪处理，再获得相位信息，而且散斑噪声的分布在空间上是不一致的，这些方法没有针对这种不一致性进行特殊处理，对于噪声分布密集的区域去噪效果可能不佳，所以本文提出了一种基于多尺度空间注意力的卷积神经去噪方法直接对带有散斑噪声的相位数据进行处理，对噪声分布不同的区域添加不同的权重以解决噪声分布不一致的问题，又结合空洞卷积和残差模块构建了密集特征提取模块提取多尺度更深层次的特征的同时避免梯度消失。通过仿真实验和微芯片焊点的热变形实验结果可以看出，该方法能够有效提高数字全息相位恢复的精度，在数字全息复杂粗糙表面的测量中具有很好的可行性。

1 方法原理及模型建立

数字全息干涉术获得的干涉图像可表达为式（1）所示：

其中，I表示全息强度图，Io和Ir分布代表物光和参考光强，和为共轭的干涉项。干涉项中包含所需的物体相位信息，为+1级项可表示为

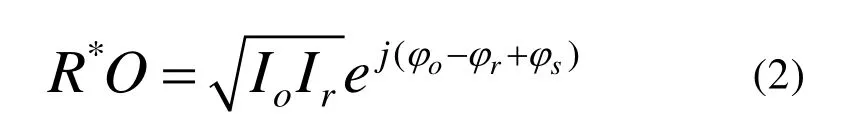
其中oφ为物体相位信息，φr为参考光相位，φs为散斑相位，当物体发生形变后，φo和sφ都会发生变化，提取出将变形前后+1级项的相位后，进行相减可得到变形相位，可表达为式（3）所示：

其中φΔ 为相减获得的相位图，Im(·)和Re(·)分别为虚部和实部，Δφo为变形产生的相位变化，ηs为散斑噪声。所以对提取的相减相位而言，散斑噪声可以表达为一种加性噪声，而干涉条纹图中的散斑噪声是以乘性噪声的形式出现，所以从原理上来看，对相位图进行去噪更加的合理。

1.1 去噪模型结构

神经网络模型实际上是一个复杂的映射函数F(·)，本文采用的是基于U-Net的卷积神经网络模型[16, 17]，并对U-Net框架进行了改进，从式（3）可得，相位与散斑噪声可表达为一种加性的关系，所需的无噪声相位可表达为：

因此，可以对噪声分布进行建模进而去除噪声。因此网络的输出可表达为：

这称为残差模型[18]，能够更好的拟合噪声的分布。主要的网络结构基于U-Net框架，由多层级的编码器和解码器构成，整体的网络模型结构如图1所示，除了基本的U-Net框架，还增加了针对噪声分布不一致问题的多尺度空间注意力模块和提取更深层特征的同时避免梯度消失的密集连接模块。

图1 所提去噪模型网络结构Fig.1 Network structure of the proposed denoising model

首先将带有噪声的相位图输入到多尺度空间注意力模块中，将带噪声的图像按照3中不同尺度进行分割，并对分割后的不同尺度不同区域的图像添加权重，以降低噪声空间分布不均匀所带来的影响，然后将3种尺度下的加权特征合并一同输入到后续的卷积层中进行编码-解码，由图1可以看出，在后续卷积操作中，为了增加模型提取不同尺度特征的能力，一共设置了4层编码层和4层解码层，每次编码使得输出的特征通道增加为原来2倍，图像尺寸下采样为原来1/4，每次解码使得输出的特征通道减少为原来1/2倍，图像尺寸上采样为原来4倍，所以最终图像尺寸又会恢复为与输入图像一致的尺寸，且每次的编码-解码过程中都引入了密集连接模块，使得模型提取深层特征的同时避免梯度消失，也在每次的编码前都合并了最开始的多尺度加权特征，以避免网络过深导致梯度消失。最后通过式（5）构建的残差观测模型，求得清晰的相位图。

1.2 多尺度空间注意力模块

多尺度空间注意力模块的结构如图2所示，首先将输入的噪声图像（1×H×W）进行三种尺度下的平均池化（1×1、2×2和4×4），分别对输入图像中1×1、2×2和4×4这三种尺度的区域计算一个权重，经过多尺度池化，特征图的尺寸分别变为原来的1、1/2和1/4大小。这些特征图尺寸大小分别为H×W、(H2 )× (W2)和(H4 )× (W4)，然后先对对这些尺度下的特征区域进行1x1空间卷积获得对应区域的权重，为了能和原来的图像(HW× 大小)相乘计算各个区域的权重，需再将权重进行插值为HW× 大小，然后将这些尺度下的权重分别与输入图像进行矩阵点乘即可得到对应尺度下的空间区域加权特征分量，可以表达为式（6）所示：

其中，ϕw为加权后的特征分量，Wφ为空间区域权重，φ为输入的噪声图像，P(·)和G(·)分别为不同尺度下的池化操作和卷积操作。最后将这些加权特征进行合并获得多尺度的加权特征如图2所示，其中颜色越深代表权重越大。引入了多尺度空间注意力模块不仅提取了不同尺度下的空间特征，也对空间不同区域进行了加权计算，能够降低空间分布不一致的散斑噪声带来的影响。

图2 多尺度空间注意力模块Fig.2 Multiscale spatial attention module

1.3 密集连接模块

密集连接模块的目的在于提取深层的特征，其结构如图3所示，输入通道数为f的特征图，通过3×3的卷积层输出固定通道数为f/2的特征图，然后为了防止梯度消失，与输入特征进行拼接后再进一步提取深层特征，如图3所示，一共经过4次的3×3的卷积层获得通道数为的特征图，然后将通道数为3f的特征图输入到3层的空洞卷积模块中，空洞卷积比分别为1、3、5，以提取三种尺度下的特征分量并合并为通道数为3f的特征图，然后为了使特征通道数与最开始一致（为了后续进行残差连接），又通过3×3的卷积层输出通道数为f的特征图，并与最初输入的通道数为f的特征图进行残差连接[18]，避免网络过深带来的梯度消失。

图3 密集连接模块Fig.3 Densely connected module

2 数据集生成与训练

考虑到实际测量过程中存在的散斑噪声和高斯噪声等因素，本文使用Matlab生成丰富的仿真数据集，仿真流程如图4所示。首先通过Zernike多项式拟合随机的形变相位分布，生成34 项Ci=(C2,C3,C4,...,C35),C1为常数项不输入网络训练，设定范围为(0,2π)，设定尺寸大小为256×256像素，进而生成变形后散斑场，与初始散斑场相减得到散斑干涉条纹图，通过相移得到带有散斑噪声的包裹图，再添加高斯噪声等因素，使数据集更加丰富逼近实际，仿真数据如图5所示。本文一共生成50000张带有散斑噪声的包裹相位图及其无噪声的标签，其中45000个数据作为训练集，5000个数据作为验证集来评价模型的训练效果。对所提的去噪网络模型进行训练时，本文使用均方误差为损失函数来使网络输出的图像与对应的无噪声图像的差异最小化。

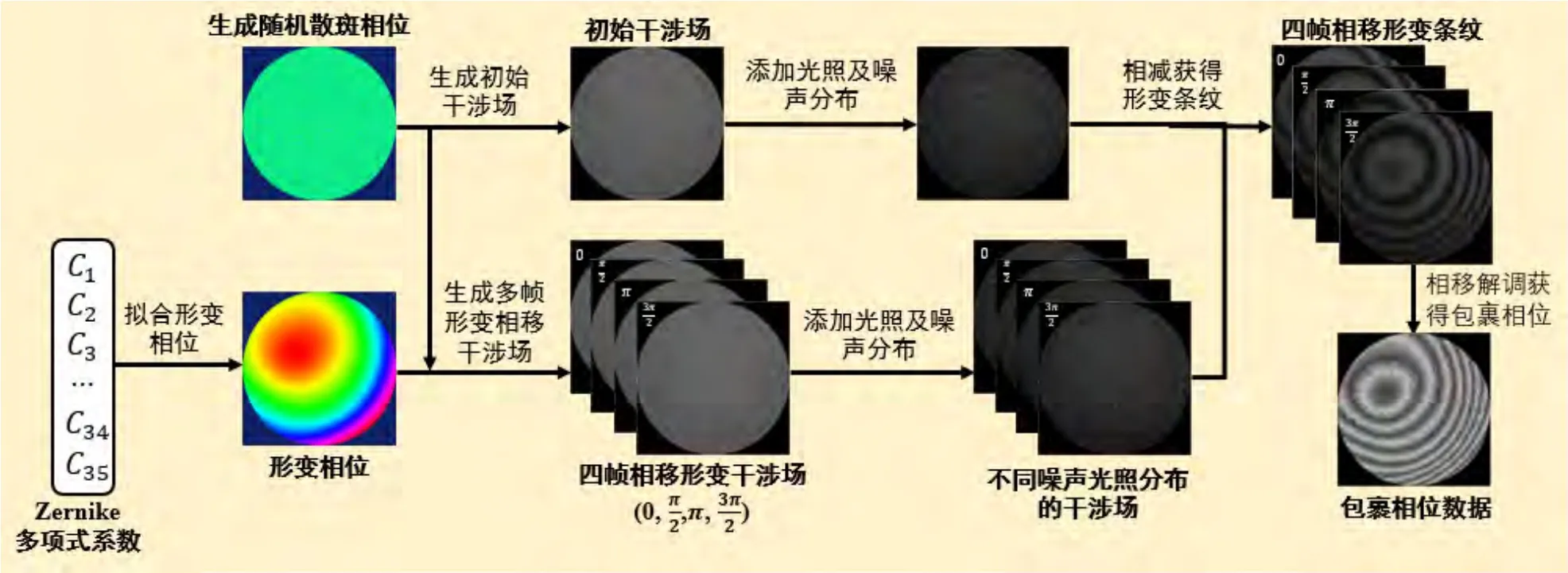
图4 训练数据生成流程Fig.4 Flowchart of training data generation.

图5 仿真噪声数据及其标签Fig.5 Simulation data with noise and labels

损失函数表达如式（7）所示：

其中θ为网络模型参数，IClear和NoiseI分别为无噪声标签和噪声图像，F(·)为网络映射函数。基于Loss (θ)采用反向传播梯度下降的方式更新网络参数，采用Adam作为优化器对网络参数进行优化，学习率设置为10-4，训练迭代次数为100，每次输入32张图像。

3 实验结果

模型训练好后，通过仿真数据和一组焊点的热变形测量数据对模型的去噪性能进行评价。首先选取了一组噪声分布较为均匀的闭条纹数据（图6（a））进行测试，去噪的结果如图6（b）所示，可以看出，原本的噪声已经被很好的去除了，恢复的图像十分清晰干净，图6（c）为恢复结果与真实标签之间的残差图，也可以看出处理的误效果很好，均方根误差只有0.0051rad。

图6 噪声较为均匀数据的去噪结果(a)均匀噪声包裹相位 (b) 去噪结果 (c) 去噪结果与其真实标签的残差Fig.6 Denoising results of data with relatively uniform noise

又选取了一组存在明显噪声分布不均匀的数据图7（a）进行分析，这组数据左上角的噪声分布相对于其他区域，更加密集，处理的结果如图7（b）所示，虽然存在明显的噪声分布不均匀现象，此方法对各个区域的均能取得较好的去噪效果，而且从残差图也可以看出，在噪声分布更加密集的区域，此方法恢复的精度依旧不亚于其他区域。

图7 噪声分布不一致数据的去噪结果 (a)不一致噪声包裹相位 (b) 去噪结果 (c) 去噪结果与其真实标签的残差Fig.7 Denoising results of data with inconsistent noise distribution

为了进一步说明此方法对于提高测量精度的效果，对去噪前后的相位恢复结果进行了比较分析，图8所示为噪声不一致数据去噪前后相位恢复结果，可以看出去噪前的相位恢复效果非常差，尤其在噪声密集区域已经完全失真，而去噪后的结果在图像的各个区域都能恢复出很好的相位信息，与真值的均方根误差仅有0.0079rad，具有很高的恢复精度。为了评价该方法在实际测量中的应用效果，本文搭建了数字全息显微系统，对芯片焊点的热形变进行测量，如图9所示。

图8 噪声不一致数据去噪前后相位恢复结果对比(a) 带噪声数据(b) 去噪结果(c) 噪声数据相位恢复结果(d) 去噪后相位恢复结果Fig.8 Comparison of phase recovery results before and after noise inconsistent data denoising

图9 数字全息显微焊点形变测量系统Fig.9 Digital holographic microscopic solder joint deformation measurement system

提取的形变相位如图10（a）所示，可以看出图像中的散斑噪声分布也是非常不均匀的，经过间断条纹估算，此形变相位的PV(Peak to valley)值约为22π（11个间断条纹），焊点的形变量可以表示为式（8）所示：

其中φΔ 为恢复的形变相位，λ为激光波长（632.8nm），为焊点的形变量。将最大形变相位估算值带入式（8）可以得到，焊点的最大形变量约为3.5µm。经过网络模型去噪后的包裹相位如图10（b）所示，可以看出该方法能够有效降低噪声带来的干扰，恢复出清晰的包裹相位，分别将去噪前后的包裹相位进行相位恢复并计算焊点的形变量，可以看出将未去噪的图像直接进行相位恢复时，由于受到噪声干扰，相位恢复算法会将噪点看作是包裹的间断以至于无法准确的对各个间断区域进行判定，计算的最大形变量（图10（c））为1.95µm，和实际出现了明显的偏差（误差约为1.5µm），而经过该方法去噪后，计算的最大形变量（图10（d））为3.45µm，符合实际的形变量分布，去噪后提高了1.45µm/3.5µm≈40%左右的相对形变测量精度，且结果更加光滑，说明该方法在实际的数字全息干涉测量中拥有很好的应用效果，能够有效的提高测量的精度。

图10 焊点热形变数据处理结果a) 焊点形变相位 b) 去噪结果 c) 未去噪计算变形量 d) 去噪后计算变形量Fig.10 Phase results of solder joint thermal deformation data

4 结论

本文提出了一种基于多尺度空间注意力的高精度数字全息散斑去噪方法。该方法在使用U-Net卷积神经网络框架的基础上，设计了多尺度的空间注意力模块，能够很好的对空间分布不同，尺寸不一致的噪声进行提取，并计算它们之间的权重，能够有效的减少噪声分布不均匀所带来的影响，也构建了空洞卷积和残差模块结合的密集连接模块，在提取深层特征的同时避免梯度消失。通过散斑干涉测量的数学模型生成大量的高精度数据集对网络模型进行训练，最后通过仿真实验和焊点的热形变实验验证了该方法的有效性，尤其在处理噪声分布不一致的数据时，能够有效的提高测量的精度，在实际的数字全息干涉测量中有着很好的应用前景。