直接多级有限元法在多尺度封装结构中的应用

赵胜军 公颜鹏 侯传涛 秦飞

（1电子封装技术与可靠性研究所，北京工业大学，北京 100124；2 可靠性与环境工程技术重点实验室，北京强度环境研究所，北京 100076）

0 引言

电子封装不断向轻质量，多功能，高性能和高集成度方向发展[1]，其可靠性问题[2-4]一直是研究的热点。封装结构的特征尺寸一般会相差多个数量级[5]，表现出明显的结构多尺度特征，例如，晶圆级封装中的TSV结构[6]，RDL层[7]等。结构多尺度特征给封装结构仿真分析带来了极大的困难，这也对当前封装结构多尺度仿真分析方法提出了新的需求和挑战。

为了解决封装结构多尺度仿真的问题，研究人员提出了各种分析方法。根据仿真模型是否为结构和载荷对称的特点，将模型简化为1/4，1/8模型或GPD模型[8-9]，但是经过这些简化后，涉及到几何多尺度的仿真模型时，其网格数量仍然很多，计算量仍然会大，甚至有时无法计算。

封装结构中的异质材料通常会使用均匀化方法[10]将其等效成均质材料。秦飞[11]等根据复合材料力学分析方法，把三维硅通孔转接板封装结构中芯片与转接板间的微凸点/下填料层以及转接板与基板间的微焊点/下填料层等效为线弹性均质材料，对等效模型进行热疲劳寿命的仿真分析。Cheng等[12]利用代表体单元（Representative Volume element，RVE）预测了复合材料的等效弹性参数。Omairey等[13]针对周期性RVE结构开发了一款Abaqus插件，用于预测等效弹性参数。以上研究只考虑了材料的线弹性参数，然而对于封装结构中表现出非线性行为的材料可能会带来较大误差。这就需要非线性多尺度分析方法对异质材料结构进行分析。

Tan[14]提出了DFE法，它是一种非线性多尺度方法，能够分析材料的非线性行为。该方法主要针对二维周期性分布的结构，无法直接应用于复杂的实际封装结构多尺度结构的仿真。因此，本文将对DFE方法进行改进，以适用于复杂的封装结构多尺度结构仿真分析。

本文基于DFE方法，提出了一种能够用于封装结构多尺度仿真的DFE-子模型方法。采用该方法对封装结构进行了有限元仿真，将仿真结果与全模型结果、子模型和局部均匀化方法的结果进行对比，说明了该方法的准确性。

1 DFE理论及其在Abaqus中的实现

1.1 DFE理论

平衡方程的弱形式[12]:

其中，u是位移；σ是应力张量；b是体力；t是面力；V、S指计算域和边界。

式(1)是虚功原理的表达式，即内力虚功 intWδ等于外力虚功extWδ。

有限元分析中，通常采用高斯积分法进行数值积分。因此，

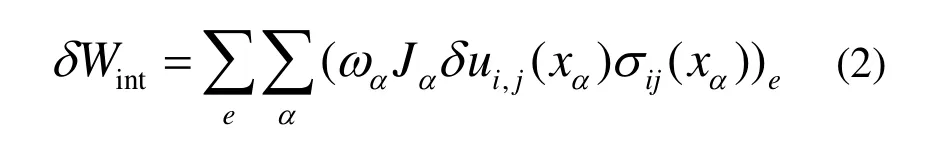
其中，α是单元e的高斯积分点。Jα是雅可比行列式；ωα是高斯点的权重。

在DFE中，每个高斯点的应力是由相应RVE的体积平均应力计算得到的。因此方程(2)可以写成：

其中，〈·〉α 表示与单元e内的高斯点α相关的RVE上的体积平均量。“～”用于表示微观尺度计算中的量。

Hill-Mandel均质化条件要求，

联立公式(3)和(4)得

把（5）式代入（1）式，得

式（6）的左边是微观的量，右边是（1）式中的宏观描述。

经有限元离散化，式（6）在有限元中表示为，

将(8)代入(7)并消去虚位移，得到

1.2 DFE在Abaqus中的实现

DFE方法在Abaqus中的实现可以通过两个关键步骤完成。

1)通过Abaqus中的多点约束（multipoint constraints，MPC），建立微观RVE边界网格节点d和宏观网格节点之间的关系。实现了从宏观尺度到微观尺度的过渡。

图1 宏微观单元Fig.1 Macro and micro scale element

RVE边界AB和边界CD节点之间的约束方程可以写成：

为了约束 RVE 的刚体平移，需要施加额外的条件，

其中，0x指在宏观单元内的高斯点，也是RVE中心的位置。

通过Abaqus中的MPC将约束方程施加到模型上，从而实现d和之间的联系。

2）缩放RVE的刚度矩阵以获得所有微观RVE组成的整体刚度矩阵。

缩放系数可以直接确定。例如，对于二维DFE分析，使用2×2高斯积分点的矩形单元进行有限元分析时

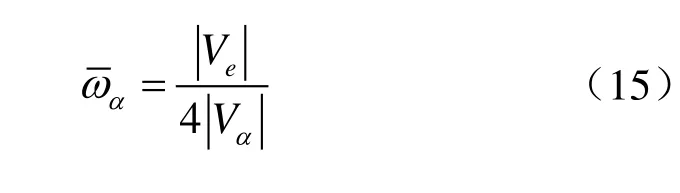
为了更清晰的描述缩放系数与DFE有限元模型之间的关系，图2给出了在宏观单元内，不同缩放系数所对应的有限元模型。模型中RVE的体积Vα一般是固定的，因此，改变缩放系数的大小，根据公式（15）可知，宏观单元体积也随之变化。

图2 不同缩放系数所对应的有限元模型Fig. 2 Finite element model for differentα

2 数值模拟

建立封装结构中的焊盘和填充料（Cu-underfill）二维多尺度有限元模型并采用DFE方法进行仿真分析。均匀化方法和子模型技术也在算例中给出，用于与DFE方法的结果比较和分析。为了验证计算结果的精度，本文用一个细化的全模型仿真结果作为参考解来计算不同方法的相对误差。

2.1 DFE模型仿真分析

算例中Cu-underfill多尺度结构全模型有3200个RVE（40*80），RVE网格模型如图3所示。RVE的长度和宽度为0.10.1mmmm× ；Cu材料在RVE的中间区域，Cu的中心与RVE中心重合，Cu的直径为0.05mm；为了保证仿真结果的准确性，对全模型进行了网格收敛性验证，当RVE的网格单元数量为457时，仿真结果趋于稳定，因此在后续的仿真中均采用该网格密度。

图3 RVE网格模型Fig. 3 RVE mesh model

2.1.1 DFE仿真模型的建立

DFE仿真模型需要把RVE模型与宏观尺度模型叠加在一起。宏观单元中每个高斯积分点上均对应一个RVE，且RVE中心与高斯积分点重合。采用MPC的方式建立RVE边界节点与宏观单元节点之间的约束，所形成的DFE仿真模型如图4所示，该模型的缩放系数为4。DFE模型的网格单元数量为365800，单元类型为CPS4R。

图4 DFE仿真分析模型Fig.4 DFE model

2.1.2 材料参数

在宏观尺度上，整个异质材料被离散化为均质的连续有限单元，宏观尺度模型的计算不需要均匀的本构关系，这是因为整体刚度矩阵完全是由RVE的刚度矩阵乘以缩放系数得到。RVE 中Cu和underfill材料参数如表1所示，underfill为线弹性材料，Cu为非线性材料，屈服应力225MPa，切线模型6666MPa。由于宏观尺度上不需要均匀的本构关系，因此，宏观模型材料参数只需要设置较小的弹性模量即可。

表1 材料属性Table 1 Material properties

2.1.3 施加边界条件和载荷并求解

DFE模型中左边界完全固定约束，在右边界所有节点上施加单向拉伸载荷， 2xmm= 。A区域的von Mises 应力和等效塑性应变分布云图如图5所示，von Mises应力值为1001MPa，等效塑性应变为0.09699。仿真分析需要的运行时间为4.8min，所需内存576MB。将该模型仿真结果（S11、S22、S12、E11、E22和E12）与全模型相应结果进行了对比，如图6和图7所示。由图可知，两个模型的仿真结果较为吻合，说明了DFE方法是有效的。

图5 DFE模型A区域仿真结果Fig.5 DFE model simulation results in area A

图6 全模型与DFE模型不同应力结果对比Fig.6 The results of different stress for DFE and Full model

图7 全模型与DFE模型不同应变结果对比Fig.7 The results of different strain for DFE and Full model

2.2 不同多尺度方法仿真结果的对比

采用子模型和局部均匀化方法[15]对2.1节中包含3200个RVE的Cu-underfill二维有限元模型进行仿真分析，RVE的网格数量、单元类型、边界条件和载荷与DFE模型一致。所得结果用于与DFE方法的结果进行比较。把全模型的仿真结果作为参考解用于不同方法相对误差的计算。不同方法的有限元仿真结果如表2所示，分析比较了仿真过程中的网格数量、内存、运行时间以及von Mises 应力和等效塑性应变的结果。不同多尺度方法对比分析的结果如下：

表2 不同多尺度方法仿真结果的对比Table 2 Comparison of simulation results for different multi-scale methods

a）子模型方法所需要的内存最少，结果的精度介于局部均匀化和DFE方法之间。

b）局部均匀化方法所得结果误差最大，且网格数量仍然较多，所需内存也较多，在三种方法中效果最不理想。

c）DFE方法是预测精度最高，所需网格数量和运行时间最少的方法，且内存占比较少，在三种方法中效果最为理想。

3 DFE-submodel多尺度方法

DFE方法主要针对二维周期性分布的结构，不能够直接应用于复杂的实际封装结构多尺度的仿真。因此，基于DFE方法和子模型技术，发展了一种DFE与子模型结合（DFE-submodel）的多尺度方法。该方法首先利用DFE方法得到等效非线性参数，然后，对等效非线性均质化全局模型进行仿真分析，最后结合子模型技术得到模型中关键区域的应力应变值。

3.1 DFE法非线性等效参数的计算

首先计算所受拉力边界上所有节点的位移值和节点反力，得到模型的载荷位移曲线；然后根据公式（16）和（17）得到名义应力应变曲线；最后根据公式（18）和（19）得到真实应力应变曲线。本算例，选择不同的缩放系数对DFE方法进行仿真，采用细化的全模型结果作为参考解，所得应力应变曲线如图6所示。根据公式（20）和得到的有限元结果可求得等效泊松比，本算例中，Cu-underfill的等效泊松比为0.3364。

由图8可知，DFE模型与全模型结果吻合度较高，能够较好的得到Cu-underfill等效应力应变关系，不同缩放系数的应力应变结果差别较小。根据应力应变关系可以得到等效的弹性模量为3.84GPa，将得到的弹塑性参数作为后续均质化模型的材料参数。

图8 Cu-underfill等效应力应变曲线Fig.8 Equivalent stress-strain relationship for Cu-underfill

3.2 DFE-submodel仿真分析

均质化等效模型仿真结束后，选取均质化模型中关键区域进行子模型仿真。子模型结构中包含RVE模型，从而可以实现对模型中微观区域仿真结果的提取。为了验证该方法的有效性，采用DFE-submodel方法对Cu-underfill结构（2.1节中的全模型）进行仿真分析。对比了18个不同区域的最大von Mises应力结果，不同区域的位置如图9所示。并且与全模型和局部均匀化模型的结果进行比较，结果如图10所示。

图9 均质化等效模型中不同区域的位置Fig.9 The locations of different areas in the homogenized equivalent model

图10 不同区域von Mises应力结果的对比Fig.10 Comparison of results for von Mises stress in different areas

由图10可知，DFE-submodel方法与全模型结果吻合度较高，相对误差在1.97%-3.97%之间，比局部均匀化方法的精度高。

3.3 DFE-submodel方法在封装结构中的应用

下面对简化后的封装结构进行仿真分析，仿真模型如图11所示。该分析过程分为两步，首先采用DFE方法对该结构的中间部分（10*10 RVE）进行均质化处理，然后对均质化模型进行有限元模拟。载荷为从25℃到150℃的升温过程，RVE结构为Cu-underfill。有限元网格及边界条件如图12所示。

图11 几何模型Fig.11 The geometric model

图12 有限元网格模型和边界条件Fig.12 The mesh model and boundary condition

采用DFE-submodel方法对该模型模拟后，读取Cu-underfill结构中Von Mises应力最大位置的仿真结果如图13(a)所示，全模型结果在图13(b)中也进行了展示，以验证该方法的有效性。从图中可以看出，DFE-submodel方法误差较小。然后，对几种方法的网格数量、所需内存、运行时间和不同方向上的应力应变都进行了对比。结果表明，本文所提出的方法能够用于分析多尺度封装结构的仿真。

图13 有限元模拟结果Fig.13 The simulation results of FEM

4 结论

本文基于DFE方法得到了多尺度封装结构的非线性等效参数，提出了一种能够用于封装结构仿真分析的DFE-submodel方法。对Cu-underfill多尺度结构的仿真分析表明，所建立的非线性等效应力应变关系与全模型的结果一致；采用提出的DFE-submodel方法的仿真分析结果与全模型结果吻合度较高。