水下环境爆炸对方形水池冲击载荷数值模拟研究

陆浩然 孙海亮 马强 李海涛 于丽晶 马明辉 孙宇新

（1 北京宇航系统工程研究所，北京，100076；2 北方华安工业集团有限责任公司，黑龙江齐齐哈尔，161046；3 南京理工大学，江苏省南京市，210094）

0 引言

爆炸水池是开展炸药毁伤评估的必要平台，也是完成战斗部破碎实验、进行水下环境爆炸毁伤能力参数测定和毁伤技术研究的重要场所[1,2]。数值仿真技术应用范围涉及各个研究领域，仿真准确性和精确性也越来越高，科学研究正逐步采用数值仿真代替部分试验。水下环境爆炸问题属于较为复杂、较难进行试验的科学研究，而且经验公式对水下环境爆炸相关问题分析能力有限，因此数值仿真方法显得尤为重要。

国内外专家对水下环境爆炸开展了大量的数值仿真：Huang H等[3]对水下爆炸问题进行了一维数值仿真，研究发现水的本构粘度系数对仿真结果有影响；钟东望等[4]将典型水下爆炸冲击波传播的试验数据、经验公式计算数据、仿真模拟数据三者进行对比，证明了LS-DYNA在该研究条件下的准确性；张斐等[5]研究表明总药量不变条件下，多次水下爆炸载荷作用下，焊接板与钢板的塑性变形形貌呈类球冠形，二者的厚度减薄率从中心位置到边界处呈先减小再增大的趋势，但焊接板的挠度小于钢板的挠度；黄兴中等[6]仿真研究建议仿真计算时的水域尺寸应该至少大于炸药尺寸的50倍；Amir Javad Moradloo等[7]采用流固耦合方法模拟水下爆炸条件下混凝土的非线性行为，分析得到混凝土坝受水下爆炸影响大小因素；Gaohui W等[8]研究了混凝土在爆炸冲击下的响应和应变率效应；焦晓龙等[9]使用ALE方法模拟了多舱室内部爆炸；Kira A等[10]将试验测得的压力与仿真所得的压力进行比对，研究表明爆炸和测点的距离与测点冲击波大小呈负指数相关性。邵旭东等[11]从理论分析、经验外推以及数值仿真、试验研究等角度，系统总结了国内外在航天产品冲击响应分析与冲击损伤/失效两个方面的研究进展，并综述分析了国内外众多学者提出的各种冲击损伤/失效评估方法在航天产品上的实用性。陈新发等[12]总结和分析了爆炸冲击波从产生到传播的各个阶段中，压力、冲量、持续时间等影响参数的理论和经验公式，获得不同比例的入射压、反射压等冲击波参数，计算了Kingery和Bulmash经验模型参数，重构了爆炸波模型。皮本楼等[13]提出了非接触式电磁激励响应板方式的爆炸分离冲击环境模拟试验方法，揭示了冲击环境预示与控制的机理，为实现电磁激励载荷作用下的结构响应的可预测提供了研究基础。目前，大部分爆炸试验水池是基于静力学理论基础设计其结构强度，但是水下爆炸作为一种高强度的爆炸冲击波，显然无法真实给出水池受力状态。本文拟采用数值模拟方法，通过模拟3kg TNT药包，在较大水池（9000mm×5000mm×5000mm）内模拟爆炸冲击过程，分析水池中冲击/应力波传播机理，揭示爆炸冲击对水池壁面作用力规律，仿真计算与分析验证了本文提出的模型方法的有效性。

1 计算模型

本文研究对象是一典型钢壁水池水下爆炸，水池混凝土墙和钢板壁使用Lagrange网格划分方法，水池内水体和空气采用Eular网格离散。

1.1 几何模型

本文的研究对象如图1所示，其中蓝色水域尺寸为8000mm×4400mm×3900mm，空水界面空气厚度为100mm，长宽尺寸与水域相同。钢池壁紧贴水域，厚度为40mm，混凝土外围尺寸为9000mm×5000mm×5000mm。模型中未显示空水界面的空气。

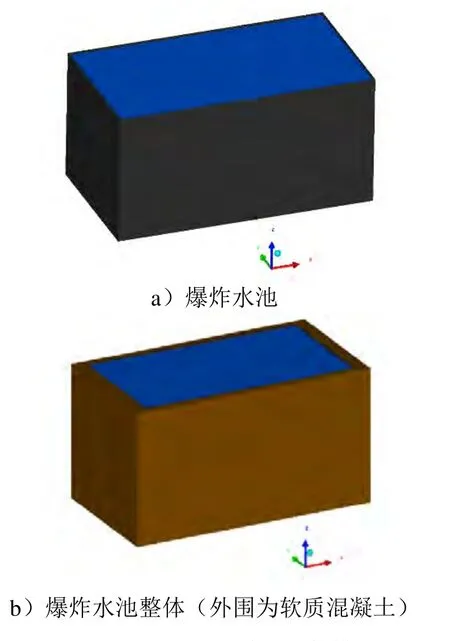
图1 典型爆炸水池整体计算模型Fig.1 Simulation model of typical explosion pool

由于本文研究冲击波在爆炸水池中的传播，计算时通过设置对称，计算模型如图 2所示。模型网格尺寸设置为20mm，建立四分之一模型4500mm× 2500mm×5000mm的空（Void）欧拉域，将水和空气两种材料对应的模型填充进欧拉域中；钢板和混凝土使用Lagrange网格划分，网格尺寸均为20mm。将爆炸冲击波映射到爆炸水池中，图2中所示炸药尺寸已经膨胀。

水池上方对欧拉域添加flow-out流出边界。钢板和混凝土通过Join连接在一起，欧拉域和拉格朗日之间使用自动流固耦合处理计算。在混凝土外围三个面（图2示右、后、下面）设置无反射边界，视为无限混凝土域。

图2 爆炸水池计算模型主视图及网格划分Fig.2 Front view and grid of typical explosion pool simulation model

1.2 材料模型

本文中涉及材料包括水、TNT、混凝土、钢、空气，均直接使用软件材料库中的材料本构方程和相应材料参数。

1.2.1 混凝土本构模型

混凝土本构模型包括失效面、弹性极限面、应变硬化、残余失效面和损伤模型五个部分。RHT的本构模型采用的Polynomial状态方程为

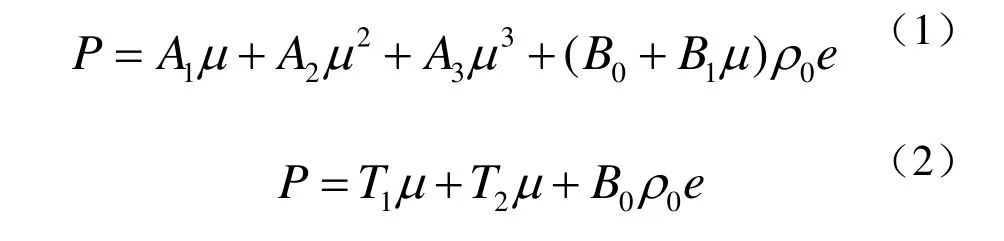
其中，e为比内能，A1为体积模量，A2、A3、B0、土，本构相关参数如表 1所示（其中除了参数B1、T1、T2为材料参数，本文选用35MPa混凝B0、B1，其他参数的单位均为kPa）。其中失效面的函数为

表1 混凝土材料参数Table1 Material parameter of concrete

式中，P为所受压力大小，P*是通过fc归一后的压力值，是P*关于 的函数，fc为单轴压缩强度，ft为拉伸强度，A为失效面的相关常数，θ是加载角度，N是失效面指数，ε˙是材料的应变率，D和α分别为材料受压缩和拉伸时的应变率常数。

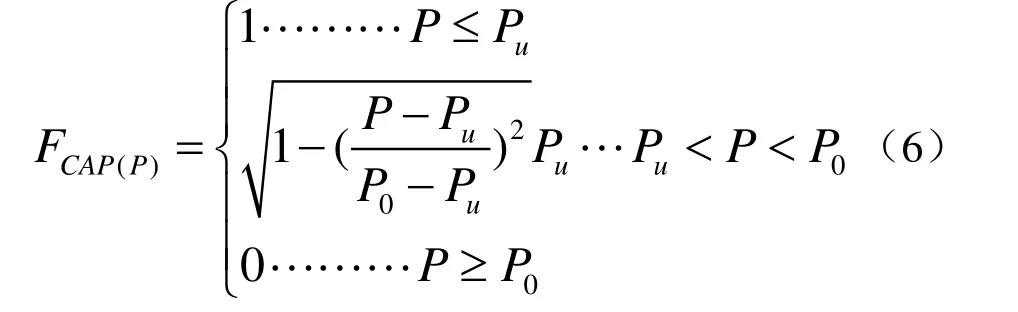
其中，felastic是弹性强度和失效面强度的比值，可以根据压缩强度cf和拉伸强度tf两参数来计算得出，FCAP(P)为常数，由具体受压力值大小来计算确定。

应变硬化屈服面参数由Y*上述失效面failY和弹性极限面Yelastic计算得出

其中G代表各状态下的剪切模量。残余失效面通过残余失效面常数B和指数M确定

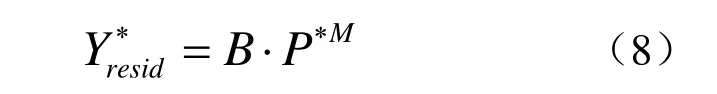
损伤模型相关计算如下

其中，Di为损伤经验常数，为最小失效应变，同时可以进一步得到损伤后的失效面和剪切模量Gfractured为

1.2.2 钢板材料本构模型

钢板使用4340钢，钢板的屈服应力yσ可以表示为

式中，εp为等效塑性应变；ε*是塑性应变率；A是屈服应力；B是硬化常数；n是硬化指数；C是钢材应变率常数；m是热软化指数；Th通过室温tT和熔化温度mT确定

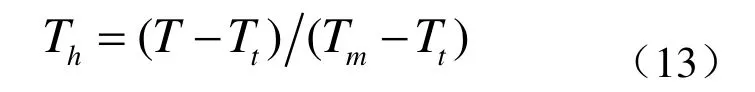
Linear状态方程如下

其中，K为体积模量。综上，钢材料模型的部分参数如表2所示（除了指数n为常数，其他参数单位均为kPa）。

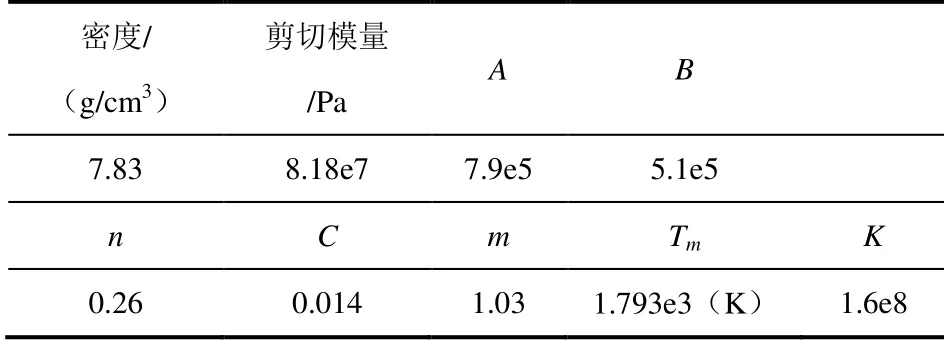
表2 钢板材料参数Table2 Material parameter of steel plate

1.2.3 空气的状态方程

空气的状态方程为以下理想状态方程

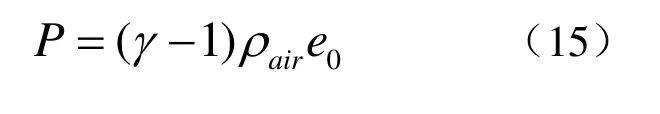
其中，P表示压力，γ表示绝热指数，0e是比内能。具体采用的参数如表3所示。

表3 空气的材料参数Table3 Material parameter of air

2 仿真计算与分析

在适用范围内经验公式所得结果高度可信，本文将以由水下自由场爆炸冲击波经验公式为基准，校验本数值模拟可信性。对于球形的TNT装药，其冲击波压力峰值为

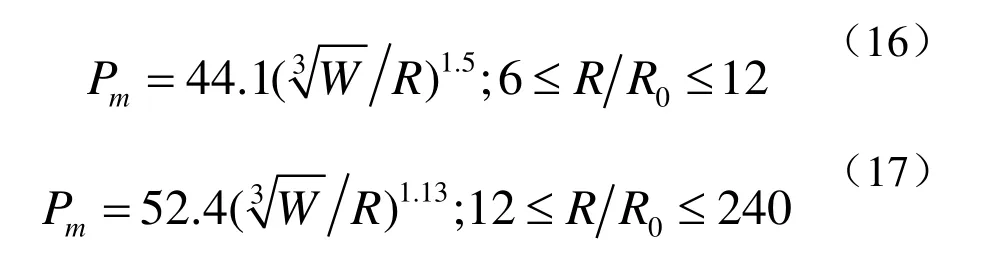
式中Pm表示冲击波压力峰值，单位MPa；W是炸药质量，单位kg ；R是距爆心距离，单位是m；0R则是装药的初始半径，单位也是m。

由于本文研究对象尺寸较大，采用Remap方法将一维楔形爆炸模型映射到三维球体模型中进行计算。当炸药位于水下的深度与装药的半径之比大于10～20，且炸药在水下的深度与装药的半径比值超过5～10时，该药量炸药在水下爆炸时产生的冲击波压力峰值可以视为不受外界影响，包括空水界面和其他介质反射等，而本文所讨论的装药位置与装药半径比值大于上述值，因此炸药爆炸短时间内可以视为自由场水下爆炸。炸药采用球形TNT炸药，炸药当量为3kg。

2.1 3kg TNT药包水下起爆后第一阶段仿真

以药包起爆开始后0.5ms内为第一阶段。3kg TNT水下爆炸模型如图 3所示，因为炸药起爆位置距离空水界面2000mm，所以楔形模型中水域长2000mm，同样添加无反射边界视为无限水域，炸药半径为76.02mm。在距爆心700mm到1100mm处，每间隔100mm设置一个，由于爆距范围为700～1100mm，装药初始半径76.02mm，根据经验公式（16）和（17）进行计算，仿真所得结果与经验公式计算结果如表4所示，数值仿真所得值与经验公式所得偏差不大于2.4%，表明计算可信。

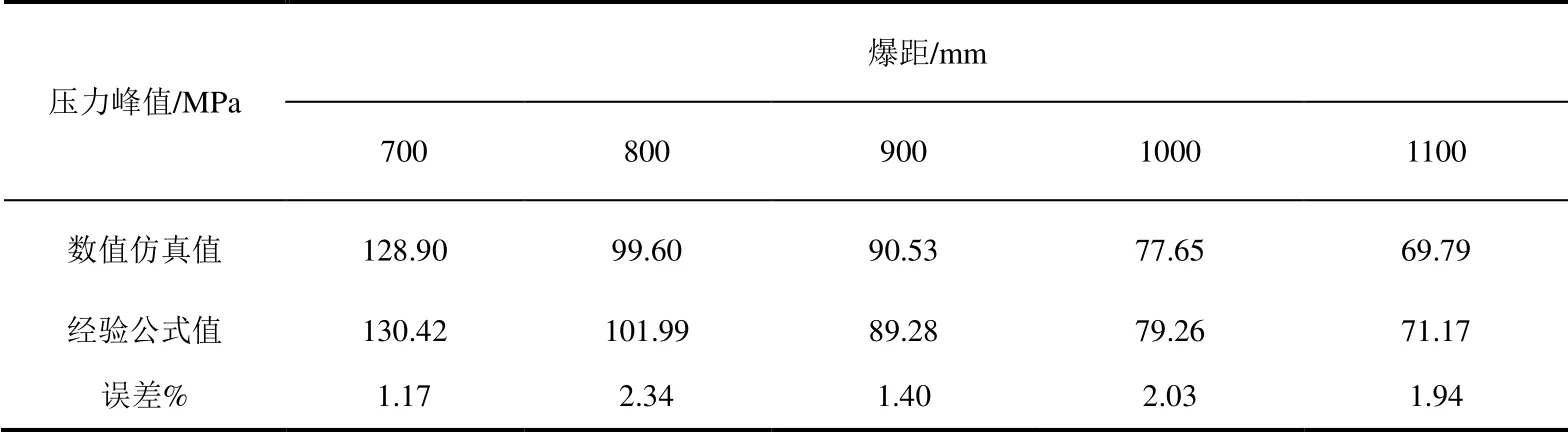
表4 3kg TNT水下起爆压力峰值Table4 Underwater explosion peak pressure of 3kg TNT

图3 3kg TNT水下爆炸一维模型Fig.3 One dimension model of 3kg TNT underwater explosion

由于本文研究的是有限区域爆炸，无限水域中冲击波计算距离不能太长：楔形模型计算到0.5ms时，输出文件并写入爆炸水池计算模型，0.5ms时刻的压力波分布如图 4所示，此时冲击波还远未到达2000mm处 。

图4 3kgTNT水下爆炸0.5ms时刻压力云图Fig.4 Pressure nephogram of 3kg TNT underwater explosion at 0.5ms

2.2 3kg TNT药包水下起爆后第二阶段仿真

由于2.1节使用的映射是0.5ms之后的爆炸冲击波数据，因此下文所提到的时间均默认加上映射前的0.5ms，所有相关曲线图的时间坐标也以0.5ms为起始坐标。

从水中压力云图可以看出炸药从起爆到0.9ms时刻，基本属于无限水域爆炸情形，爆炸冲击波呈球形向外传播；冲击波在1.1ms左右传播到空水交界面和水池底部钢板，因为空气介质的密度和声速都远小于水介质，所以空气介质的波阻抗远远小于水介质的波阻抗，那么此时主要是产生与入射波方向相反的反射波，而透射波数值较小，这从图中可以观察到，冲击波传播到空水界面时发生反射产生方向相反的反射波，而由于压力显示区间问题，导致较小的透射波从云图中不易观察到；而水池底部的交界面处，水介质的波阻抗小于钢介质的波阻抗，可以看到钢壁与水交界处的确出现了红色高压区，而继续往下传播的是透射波，此情况下，透射波大小大于入射波。图 5（d）的三处红色高压区也是因为上述波阻抗不同的原因形成的，但是从池底处依然可以发现出现了与入射波方向相反的反射波传播轨迹，这是因为水下爆炸是很多方向冲击波的叠加。图 5（e）-（g）主要是冲击波传播到较近钢壁和池底的反射与向较远钢壁的类球形传播过程，并且图示左方与下方的冲击波相遇形成高压力区，而后又沿着各自方向继续传播。从图 5（h）开始，主要是反射波之间的碰撞叠加，随后继续传播又反射，循环进行，直至压力最终消耗殆尽。

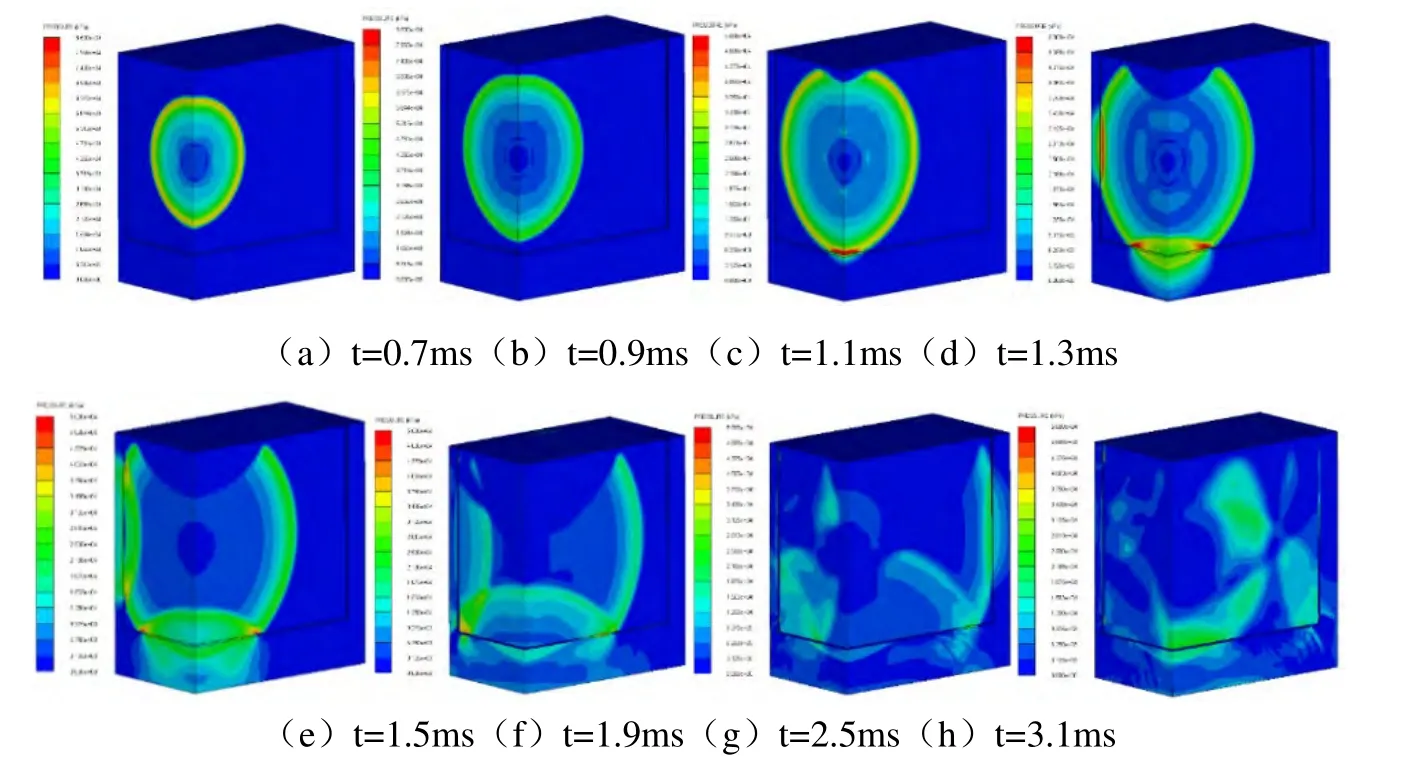
图5 3kgTNT水池中爆炸压力云图Fig.5 Stress nephogram of 3kg TNT underwater explosion at test pool

图6是将水域隐藏后的池壁等效应力云图，目的是观察钢壁在炸药爆炸短时间内的应力变化。炸药起爆后1.1ms，离爆心最近的池底最先开始产生应变；随着爆炸冲击波呈球形向四周传播，钢壁上对应的应力峰值也呈圆形向外传播，如图6（b）、（c）所示；图6（d）和（e）呈现了冲击波在两钢壁夹角处的叠加同样使拐角交界处的应力产生叠加，产生了应力集中，如图6（e）中红色区域所示；图6（f）的应力云图变化，说明冲击波的反射同样体现在了钢壁的应力变化趋势上；从最后两张图中可以看出，后部分时间钢壁应力体现在较远壁处，且应力最大的是三钢板交界处，因为在这些地方会发生应力集中。另外，从图6（g）和（e）中可以发现钢壁距离池底越近处应力越大，这主要是冲击波在空水界面发生卸载导致的。

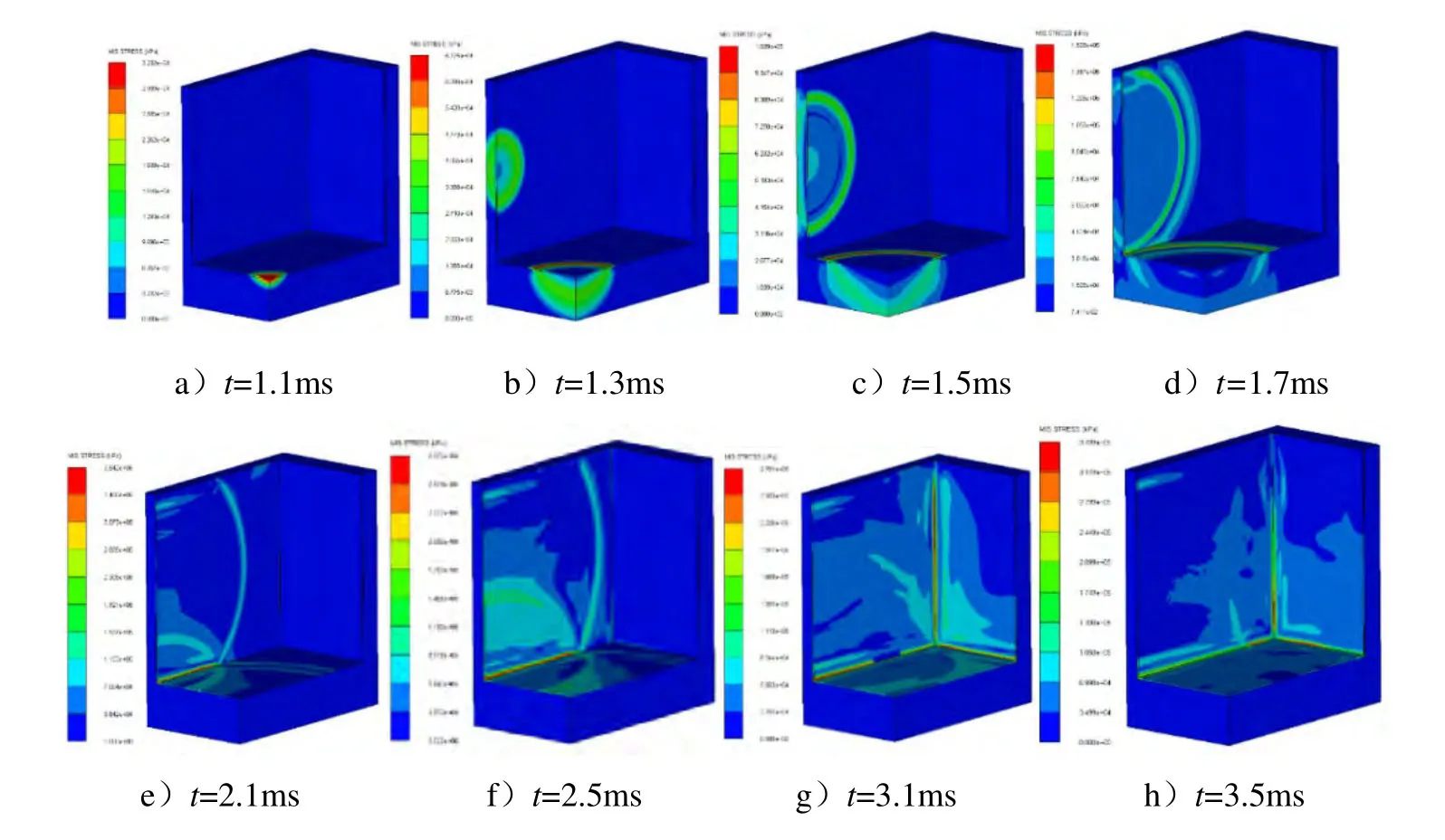
图6 3kgTNT水池中爆炸池壁等效应力云图Fig.6 Equivalent stress nephogram at pool wall of 3kg TNT underwater explosion

2.3 各观测点应力分析

本文研究对象所设置观测点如图 7所示：其中1～5号高斯点为钢壁靠水表面观测点，1号点与装药中心在同一水平线，1、2、3点处于同一水平线，间隔1000mm。1、4、5号点在同一竖直线上，同样也间隔1000mm。6～8号点为水域中的定观测点，三个点与爆炸中心在同一水平线上，与爆心距离2000、3000和4000mm；9-12号观测点同样在钢壁上随动，水平位置和间距与1～3号点一致。

图7 计算模型高斯点设置Fig.7 Gauss points of simulation model

2.3.1 水中压力传播分析

冲击波在水池中传播的大致规律，6～8号观测点对应的时间—压力拟合曲线如图8（a）所示。图（a）和（b）的不同点在于，（a）是在爆炸水池中传播、（b）在无限水域中传播，图 8（a）的6、7、8点对应图8（b）的1、3、5号测点。因为爆炸冲击波传播到池壁时会产生各个方向的反射波，且会产生多次反射，因此图8（a）情况的后面时间段的冲击波压力变化曲线错综复杂。但是相同的是，6～8点在3.5ms左右第一段波基本也趋于0，与图 8（b）相同，且6号与1号、7号与3号点第一次到达波峰的时间与大小都几乎相同，但是8号与5号观测点虽然到达波峰时间一样，但是8号观测点的压力大小明显大于5号点，甚至超过了爆距更近的7号点处冲击波压力，从图8（g）中可以发现，是因为2.43ms左右在8号测点产生了反射波，冲击波叠加，使得该峰值大小“异常”。

图8 （a）6-8号高斯点压力变化拟合曲线（b）无限水域情况压力曲线Fig.8 (a) Pressure fitting curve at Gauss point 6～8 (b) Pressure of infinite fluid

2.3.2 池壁各点处等效应力曲线分析

图9是离爆心较远处的钢壁上观测点随时间变化的等效应力（MIS.STRESS）曲线，由于3、5点处应力集中，应力峰值较其他观测点较大，为了便于观察单独拟合，下文对1-5号测点的应力变化曲线也分开拟合。

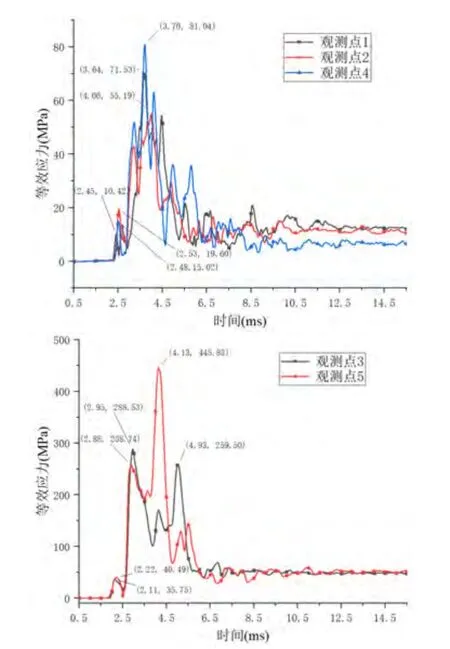
图9 无防护措施下1-5号观测点处等效应力曲线Fig.9 Equivalent stress nephogram at point 1～5 without protective measure

1、2和4 号观测点第一个波峰到达时间相差不大，数值上1处最小是因为他的峰值到达最早，此瞬时的冲击波对钢壁的应力影响还未传递到2和4，所以冲击波随着时间推移传播到2和4点 时，会产生一个叠加后的波峰，自然就比前一时刻1处的应力峰值高。而对于每个测点处的最大应力来说，4＞1＞2，可以推断出爆炸水池爆炸时，同一水平线上，爆距越近，钢壁的最大应力越大， 而竖直方向上，因为空水界面对冲击波的卸载，以及池底的反射作用，反而距池底较近但离爆心较远的4号点处的最大应力更大。5号观测点第一个波峰略高于3号观测点，两点处的最高波峰可以视为有两处，图中均已标注出来，且总体压力峰值远大于3号位置，是因为3号位置距离水面较5号近，许多冲击波传播到空水界面发生卸载，同时冲击波传到池底会波及到5号测点。

根据3.2节对云图的初步分析，距离爆心较近钢壁上的应力到6ms之前就已经达到峰值了，9-12号观测点等效应力拟合曲线如图 10所示，结合图6中不同时刻钢壁应力云图，各位置第一次波峰到达时间是匹配的。同样地，爆距越大，第一个波峰应力大小越大（图示中11和12号观测点的第二个波峰视为第一个波峰，可能是因为应力叠加的时间相差较大出现两个波峰），这是因为冲击波初步传播过程，随着时间的增加，越晚到达的位置受到应力叠加影响越大，从而使得应力越高；第二个标注出的峰值是较近池壁与池底冲击波叠加后传播到各观测点产生的，如图 5的最后三张图所示，第二个压力峰值即是各点处的最大应力，对于各点处最大应力的大小而言，观测点位置离爆心越近，钢壁的应力峰值也就越大。

图10 无防护措施下9-12号观测点等效应力曲线Fig.10 Equivalent stress nephogram at point 9～12 without protective measure

3 结论

本文开展了爆炸冲击对水池壁面作用力数值仿真，揭示了爆炸冲击波在水池中会发生多次反射机制，得出了水池壁面受力规律：各池壁交界处，由于应力集中，应力明显大于钢壁中心区域；不考虑应力集中区，同一水平线上，距爆心越近，应力越大，而同一竖直线上，因为水池上的空水界面对冲击波的卸载作用，加上冲击波传播到池底发生反射后继续向侧面池壁传播，因此距爆心越近但是离池底越远处的应力反而越小；较远池壁整体X方向最大位移是0.65mm，最大的正向加速度是 1.01e3m/s2，最大反向加速度是0.64e3m/s2。