碎石土斜坡水平受荷桩m取值研究

徐显涛，杨 洵，徐久燕，陈继彬，赵其华

(1.重庆南江工程勘察设计集团有限公司，重庆 401141； 2.中国建筑西南勘察设计研究院有限公司，成都 610052； 3.成都理工大学 环境与土木工程学院，成都 610059)

1 研究背景

西南地区输电线塔工程的基础(桩)所处地形坡度多在30°左右(如图1所示)，且以碎石土类斜坡最为常见，成因可分为坡积、冰蹟、泥石流堆积等，工程特性主要为块体大小不一、土层厚度不均匀、土体强度高、变形小、渗透性好。在坡上或临近斜坡顶部设置工程结构(桩基础)时，桩基础除承受上部线塔的竖向力外，还承受桩后土压力、风、地震、电线断线等作用产生的水平作用力，对斜坡桩-土相互作用产生了较大的影响。

图1 穿越斜坡场地的工程示例(桩)

在研究桩-土体系水平受荷时，广泛应用的是计算方法简单的弹性地基梁m法。对于中密、密实的砾砂、碎石类土，该法应用相对广泛，但是m并不容易准确获得，桩侧土体位移的获取更多的是依据现场试验。规范[1]、手册[2-3]中所建议m的取值范围较为宽泛且建议值仅适用桩的泥面位移较小(中密、密实的碎石土类为1.5～3.0 mm)的情况，诸多工程结构在受力后其位移量远>3.0 mm这个位移极限，当位移较大时应如何取值？多年来研究者们试图解决这一问题，开展了大量试验，取得了较为丰富的个案，建议了砂土、粉土、黏性土在不同密实度、不同含水率时的m值取值范围[4-8]。

上述研究成果主要针对水平场地，如将成果应用于斜坡场地往往会造成很大的结果偏差，弯矩误差最大可达到20%～30%，变形误差可达到实测值的150%～200%[9]，主要是因为斜坡坡度的变化严重影响了桩身浅层土体的水平抗力[10-12]。基于此学者[13-15]对黏性土、砂土中弹性桩通过一系列的数值模拟分析得出不同坡度、不同深度m与水平场地的比值关系，绘制了查询曲线。而碎石土斜坡场地，研究重点则主要是修正了规范[1]中m计算公式的相关参数，如桩身计算宽度、荷载大小、荷载位置、允许位移等[16-18]，所得结论均未脱离弹性地基假定，亦未在工程中得到有效印证。

综上，目前几乎未见碎石土斜坡水平受荷桩m取值可供借鉴的成果，且相关规范也没有给出不同坡度情况下斜坡地形m的取值范围和计算方法。

本文在查阅大量文献的基础上，结合相似理论，设计并开展了4种坡度(0°、15°、30°、45°)下室内模型桩水平载荷试验，研究斜坡桩-土受力变形特点，重点分析不同坡度时m随桩身泥面位移的变形规律，从而建立经验计算公式；并参考坡度对桩侧土体抗力变化规律的影响，深入探讨m计算关系式中各计算参数的确定方法，以此来提高斜坡场地结构水平抗力计算的精准度。

2 室内模拟试验设计

2.1 斜坡体模型设计

(1) 斜坡坡度设计：试验坡度为0°(水平场地)、15°、30°、45°。

(2) 坡体材料设计：试验用土取自四川省理县薛城镇某高陡斜坡场地碎石土，稍密—中密，粒径一般为3～8 cm，棱角状，磨圆度差，块石之间充填少量黏性土及砂砾(见图2)。采用灌水法、室内土体剪切试验法和烘干法测定土体密度、黏聚力、内摩擦角及含水率，所得参数见表1。并根据室内筛分试验结果确定级配比例为粒径>2 mm的颗粒占73.6%、粒径>5 mm的颗粒占60%、粒径>20 mm颗粒含量为28.8%。

图2 坡体材料照片

表1 碎石土物理力学参数

2.2 模型桩设计

试验相似比根据输电线路工程常用桩基尺寸、室内模型试验台尺寸、试验边界约束条件进行确定和设计，详情如下。

(1)原型桩基尺寸：西南山区输电塔基础90%以上为人工挖孔桩基础，截面宽度为0.8～1.2 m，桩长为8～10 m。本次试验选择原型桩桩长10 m、桩径1 m、桩身混凝土强度等级C25。桩身主筋和箍筋分别HRB400和HPB300，主筋直径28 mm(30根)、箍筋直径8 mm(间距200 mm)。

(2)模型试验台尺寸：三维地质模拟试验台尺寸为3 m×2 m×1.5 m(长×宽×高)，如图3(a)所示。

图3 试验槽及模型桩

(3)边界条件：下坡向为9b(b为桩宽)长度，上坡向为5b，左右两侧为4.5b。

综上，确定试验相似比为10，模型桩几何参数见表2。试验桩用材料配合比为水泥(42.5R)：砂：水=1∶1.76∶0.32。桩身配筋采用主筋和箍筋直径分别为6 mm和2 mm，主筋用量4根，箍筋布设间距10 cm。制备后模型桩材料的密度2.14 g/cm3、弹性模量为27.83 MPa、单轴抗压强度为49 MPa。试验模型桩见图3(b)。

表2 桩模型设计参数

2.3 试验过程

(1)试验组数。每种坡度下试桩1组(每组1根)，共4组。

(2)试验模型的安装。模型试验槽标记好尺寸刻度后，分层夯实填土至密实度60%(每次堆土20 cm，夯实到15.7 cm，计算方法参见规范[19])。填筑至模型桩底标高时固定模型桩，然后重复分层夯实填土。填筑完成后刷坡成试验坡度。试验模型如图4所示。

图4 试验模型

(3)监测元件的埋设。在埋桩过程中，同步埋设桩顶位移百分表和桩侧土压力盒。其中：①在桩顶及桩顶下10 cm处分别架设两只百分表测量桩顶和泥面位移；②土压力盒桩前布设5只，从泥面处向下间距15、10、10、15、15 cm；在桩后从桩底向上间隔10、15 cm布设3只。

(4)加载及停载。在泥面处安装千斤顶施加水平荷载，加载方向为坡体临空方向(即从坡后向坡前加载，见图4)，反力架为试验槽框架。加载方式为慢速维持加载法，按0.3 kN/级递增，每级荷载施加完成后稳压5 min测读桩顶水平位移、桩侧土压力。当桩前土体破坏(隆起或裂缝明显)或桩顶位移>40 mm停止试验。

3 桩身变形及土体水平抗力

3.1 桩顶位移-荷载关系

图5为试验过程中桩顶水平位移-水平荷载关系曲线。相关数据统计见表3。

图5 不同坡度桩顶水平位移-水平荷载关系曲线

表3 不同坡度桩顶位移-水平荷载曲线特征数据

由图5、表3可见：不同坡度下，荷载-位移曲线形式几近相同，表现为桩身变形随荷载、坡度增大而增大。达到同一变形量所需荷载随坡度增加而递减。如桩顶水平位移为30 mm时(图5)，坡度自0°→15°→30°→45°渐增时，所需水平荷载降低幅值分别为15%、27%、45.2%。

桩土体系相互作用阶段会随荷载变化而变化，结合图5曲线拐点，按照相同荷载增量(Δp)下的位移增量(Δs)将桩顶受荷变形分为线性阶段变形、非线性阶变形段、加速阶段变形。其中：①线性变形阶段，随着荷载增大，桩顶位移近似线性增大，荷载每增加0.3～0.5 kN，桩顶位移相对前一级荷载增大0.2～0.4 mm；②非线性变形阶段，荷载在临界和极限荷载之间，荷载每增加0.3～0.5 kN，桩顶位移相对前一级荷载增大0.5～10 mm；③加速变形阶段，桩顶荷载进入极限荷载后阶段，荷载每增加0.3～0.5 kN，桩顶位移相对前一级荷载增大约为2 cm。

各阶段标志点对应荷载、位移数据见表3。由表3可见，随着坡度的增大，各阶段标志荷载在逐渐降低。经统计，坡度每增加15°，所需荷载近似按15%的等比递减。即触发相同桩顶位移的水平荷载与斜坡坡度呈近似定量的反比关系。

3.2 土体水平抗力-荷载-桩深关系

各级水平荷载作用下桩侧土体水平抗力(土压力)随深度变化关系曲线如图6所示。

由图6可见，整体上，土体抗力在深度方向上先增大后减小，呈“凸”型变化。抗力随深度变化主要分为2个阶段：①桩侧土体抗力从泥面处开始逐渐增大，达到最大值后(最大值深度约为(0.3～0.5)h′，h′为桩埋深)逐渐减小，直至0 kPa；②由于基础(桩)发生挠曲变形，桩后土体亦会产生抗力，表现为随深度增加而增大，桩底为极大值。从图6可见，桩侧土体抗力0点即为桩身变形拐点。

图6 不同坡度桩侧土压力-桩深曲线

另外， 随着坡度的增大， 土体抗力最大值逐渐降低的同时最大值深度逐渐下移， 进一步整理得出不同埋深桩单位面积上的土体抗力(极限抗力与埋深、 桩宽的比值， 表示为Pmax/(z·b))， 结果见表4。

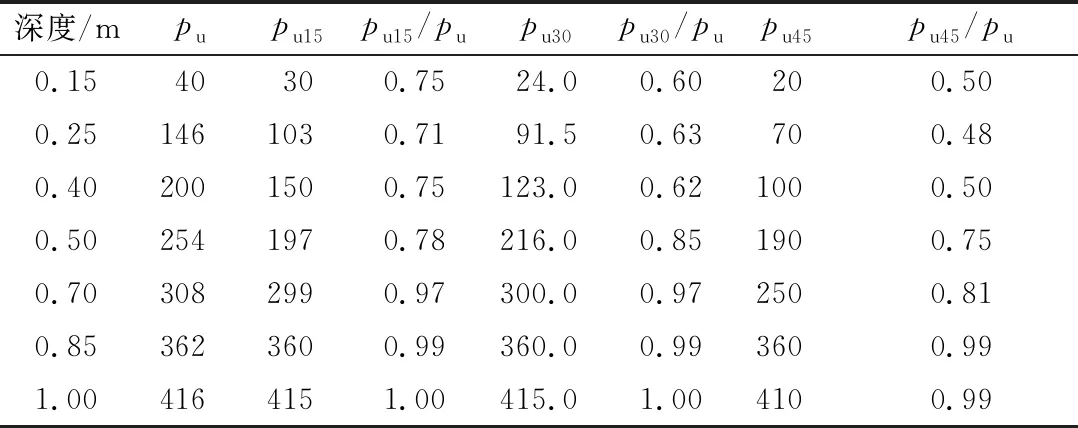
表4 不同埋深桩侧单位面积上的土体抗力

从表4可见，每一坡度下的puθ(θ=15°、30°、45°)与水平场地下pu比值分2段：

(1)抗力最大值深度((0.3～0.5)h′)至坡面处，两者比值近似为常数，该比值仅与斜坡坡度有关，坡度15°、30°、 45°时，其比值近似分别为0.75、0.61、0.49，可近似表述为

(1)

(2)抗力最大值深度至桩底处，两者比值近似为1，即不受斜坡坡度的影响。这表明斜坡坡度消弱了桩侧土体抵抗桩身变形的能力，这一影响主要表现在抗力最大值深度至坡面处。在斜坡场地进行桩基础等结构设计时，不能按照水平半无限空间场地进行考虑，需要按式(1)对该段土体抗力进行相应的折减；而该深度以下土体抗力可按水平场地的情况考虑。

4 斜坡场地m的确定

4.1 m与泥面位移关系

规范[1]认为m取值与实际荷载、允许位移相适应，如果根据试验结果求桩的m，应采用Hcr和Xcr进行计算，建议采用式(2)求取地面以下的综合m，得到m随泥面位移(y0)变化的关系曲线，如图7所示。

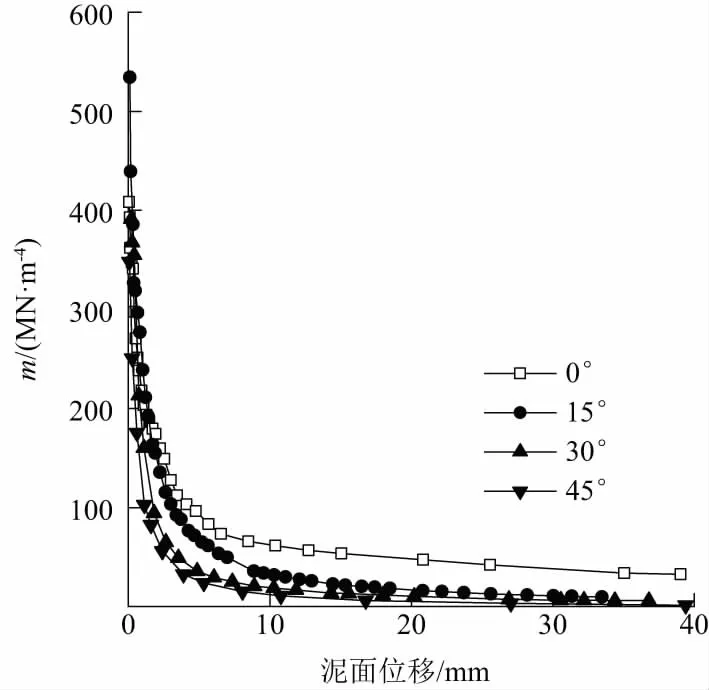
图7 m随y0变化曲线

(2)

式中：m为土体水平抗力系数的比例系数(MN/m4)；Hcr为临界荷载(kN)；Xcr为Hcr对应的位移(m)；νx为桩顶处的位移计算系数，按规范取值；EI为桩抗弯刚度(MPa·m4)；b0为桩身计算宽度(m)，与桩截面几何形式和桩径d有关。

按试桩的地基土进行分类，确定m的取值范围应为100～300 MN/m4(泥面位移y0为1.5～3.0 mm)，但是从图7可见，泥面处桩身发生3 mm位移时计算得到的m明显小于规范建议值，主要是因为斜坡坡度效应所致，即笔者[10]和赵明华[12]所认为的陡坡效应影响深度。根据图7中m随y0变化表现出的幂函数衰减关系，进一步拟合得到其表达式为

(3)

式中：y0/b0为土体应变；b0为桩宽度(或直径)， 按规范[1]建议取值；Cm为土体发生单位应变时相应的m取值；k为m随y0增大而减小的幅度。

4.2 k的确定

4次试验均可拟合得出相应的k1、k2、k3、k4，系数k表示m随y0增大而减小的幅度，每一种土体k并不相同，图8给出了本次试验土体的k拟合值区间曲线。可见，本次试验所用碎石土k为-0.8～-1.0，可按常数进行近似拟合。因此式(3)可以改写为

图8 k取值

(4)

4.3 Cm值的确定

同样的，4次试验均可得到相应的C1、C2、C3、C4，系数Cm与m量纲相同。实际上，m的变化主要是桩侧土体在深度上所能提供的抗力效能不同而导致的，如若叠加斜坡坡度的作用，又会进一步削减土体抗力的发挥程度。文克勒弹性地基理论假定，桩在受到水平荷载作用时，常把土体视为线性变形体，水平抗力所受的桩土摩擦阻力的影响可忽略不计，假定某一深度z处的桩前土体水平抗力px等于该点的水平抗力系数kx与该点的水平位移x的乘积；同时，假定kx随深度线性递增，即kx=mz。可以得到理论上的m计算式为

p=mzy。

(5)

对比斜坡场地下同一深度Cm|斜坡与水平场地条件Cm|水平之间关系，得到式(6)。

(6)

由3.2节可知，每一坡度下的puθ与水平场地下pu0比值呈2种关系，即

(7)

式中zmax为抗力最大值深度。根据桩顶位移计算m，最终计算公式可表示为

(8)

5 试验验证

图9 场地地形地貌及桩位

试验用油压千斤顶Pmax= 2 000 kN，Ymax=200 mm(最大伸出量)，精度0.5 MPa，在桩顶泥面处进行慢速维持水平加载，按桩基极限荷载的1/10每级施加。

埋深桩身侧写仪监测桩身水平位移，桩顶布设百分表监测桩顶位移，桩侧土体埋设土压力盒(桩前间隔1 m)监测土体抗力。每集荷载施加稳定后按30 min 间隔测读试验数据，当桩顶位移<0.1 mm/h后施加下一级荷载。当桩身断裂或桩前土体失稳破坏停止试验。反力装置采用尺寸4 m×3 m×1 m(高×宽×厚)的C25混凝土墙，埋设入土2 m。混凝土反力墙与桩间距约为30 cm。为防治加载点应力集中在反力墙与千斤顶之间、千斤顶与试桩之间分别铺垫3块厚2 cm的方形钢板。如图10所示。

图10 原位试验示意图

试验结果见图11，最终根据水平荷载-泥面位移关系计算m，计算结果见表5。

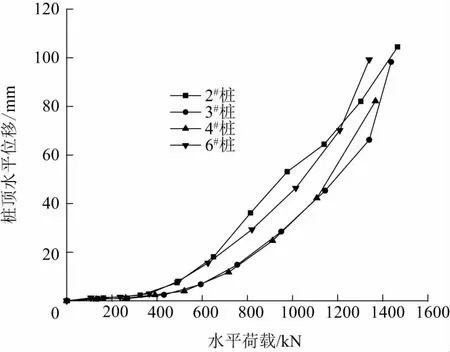
图11 泥面位移与水平荷载关系曲线

表5 不同方法下m计算结果对比

从表5可见，计算结果及监测结果对比，在计算斜坡单桩水平位移时，本文所提方法计算m与监测所得m相近，差异范围多在20%以内。需要注意的是：式(4)中b0为桩基的计算宽度，计算按规范[1]建议取值，而斜坡坡度对该参量有一定影响，尤其对陡坡影响越大，本文并未对此进行探讨，也是造成计算结果误差的原因之一。总体来说，计算值与实测值吻合得比较好，本文方法为一种计算m的简易算法，计算结果可以用于碎石土斜坡桩基的设计计算。

6 结 论

碎石土斜坡水平受荷桩m的合理取值研究是工程界亟待解决的科学问题。基于此，本文采用室内模拟的手段，研究了4种坡度下水平受荷载桩受力变形特点，来获得斜坡坡度对m的取值影响。研究结果表明：

(1)加载过程中，荷载-位移曲线形式相似，受坡度影响较小，表现为桩身变形随荷载、坡度增大而增大。达到同一变形量所需荷载随坡度增加而递减。

(3)斜坡碎石土场地水平受荷桩的m随泥面位移变化呈现幂函数衰减关系；根据斜坡场地和水平场地的桩侧土体水平抗力的比例关系，提出了斜坡场地m简易计算公式，计算方便、精度高，可以很好地表征碎石土斜坡桩基在水平荷载作用下的受力特性。