概念层次开发在产品概念设计多属性决策方法中的应用
2022-12-02裴卉宁谭昭芸黄雪芹温志强杨冬梅
裴卉宁,谭昭芸,黄雪芹,温志强,杨冬梅
(河北工业大学建筑与艺术设计学院,天津 300401)
目前,在产品设计及概念方案决策层面的协同开发过程中,产品概念设计方案的生成过程大多基于专业规范、设计案例、用户反馈、实例运行、售后维护等基本数据进行统计分析、实验建模以最终确定[1]。由于缺乏有效的专业决策工具与多属性设计方法学的支持,决策专家在专业知识、教育背景、科研能力、研发策略等多方面存在差异,因此往往导致最终的产品概念设计方案存在一定的差异性与多样性[2]。如何针对众多备选产品概念设计方案(下文均以“备选方案”代称)进行科学合理、客观有效的决策,对于综合考虑产品概念设计的需求将具有一定的现实意义。
针对所提出的产品概念设计方案决策问题,国内外有关学者展开以下研究。Inoue 等[3]提出在设计过程的早期阶段基于设计者的知识或经验获取用户偏好,为可持续产品创造提供决策支持;Lennon 等[4]通过微等离子体设备的概念设计案例,建立了兼具效率性、有效性和总体效用的评价指标体系,并建立了面向工程产品的多属性决策系统;宫金良等[5]为了解决复杂产品概念设计过程中设计需求参数的模糊性和不确定性等问题,提出了一种基于理想度与粗糙集理论多属性决策的复杂非线性系统设计方法;陈英等[6]提出了一种基于细粒度设计理性模型的群体一致性产品方案多属性群体决策方法,能够将选择产品备选方案和决策过程进行有效结合;孙朋[7]等根据不同方案前景值中理想解的收益和损失情况,建立了一种犹豫模糊环境下属性权重未知的多属性群决策方法;Kruse等[8]提出在工程设计的概念开发阶段,使用系统建模语言(Systems modeling language,SysML)一次提供多种潜在的解决方案;Qi 等[9]提出了一种基于粗略距离的评价方法,该方法重新定义了理想解的概念(Rough distance to redefined ideal solution,RD-RIS),并从用户偏好信息中获取与用户相关的评价权重和其重要性等级;Tiwari等[10]提出使用软集理论和香农熵获得设计规格和客户需求的信息,并与TOPSIS框架融合用以识别方案评价过程中的最佳备选方案。
但在产品概念设计方案决策研究方面存在部分不足之处。1)现有研究主要是从总体上对各备选方案的多目标评价指标进行简单的线性累加,并根据各产品概念设计方案的总体评价分数进行排序,导致最终的产品概念设计方案并未具备最高权重的设计功能与特点,故缺乏能够综合考量各产品概念设计方案系统层级结构中设计指标的多属性决策方法。2)目前研究各备选方案的最终得分多是根据评价指标单独得出,对于各备选方案的相互比较得分考虑不足,可能导致出现具有相似优秀品质的备选方案被淘汰的情况,因此缺乏各备选方案多属性之间关系的明晰对比。
综上所述,为了综合考虑各备选方案多属性系统层级结构的相互关系,提出一种基于概念层次开发(Concept hierarchy development,CHD)的产品概念设计多属性决策方法。将各产品概念设计方案进行层级划分并逐级展开,构建各层级内的具体设计特性比较矩阵,通过引入融合毕达哥拉斯模糊集(Pythagorean fuzzy sets,PFS)和前景理论(Prospect theory,PT)的方法,对决策专家及设计准则进行合理科学的权重分配,最终对各备选方案进行总分排序,为产品概念设计中的多属性问题提供了一种客观有效的解决方法。
1 基本概念
1.1 CHD理论
在当今消费需求快速变化的经济市场竞争中,产品概念开发设计阶段是满足产品的多样化和创新性的关键步骤[11-13]。如Hwang 等[14]提出了一种辅助产品设计师满足特定设计目标X需求(DHSfXs)的备选方案辅助开发工具;武春龙等[15]提出在概念设计阶段应用发明问题解决理论(TRIZ)中的功能模型和层次分析法(AHP)构建智能产品服务系统概念方案创新设计方法。然而,以往的相关研究着重于探索产品概念设计早期阶段的用户需求偏好与功能结构优化等方面,未将品概念设计后端的产品模块结构与多属性决策二者进行综合考虑,最终难以对各备选方案在概念层次中的联系与相似度进行考量和分析。故在产品概念设计多属性决策步骤中,使用CHD理论[16]能够系统化地对各备选方案的产品模块结构进行多层次的开发,通过对各备选方案的产品模块结构相似度进行两两比较,获得不同层次的重要性权重,最终对各备选方案进行全面的综合评价。
提出基于CHD的产品概念设计方案划分框架(如图1所示),绿色菱形代表不同的产品概念设计方案,根据张雷等[17]在产品绿色设计方案优化方法中绿色属性与模块实例之间的映射关系,对备选方案图像进行清晰的级别划分,提出在各备选方案的模块和属性级别间添加角度视图的设计层次开发级别,将各备选方案的图像分为模块部件、角度视图、物理属性3个设计层次开发。第1个设计层次开发为模块部件,每个备选方案可分为若干模块部件设计,以备选方案中包含3个模块部件为例,图1中红色、蓝色和紫色3个颜色区域分别代表不同的模块部件;第2个设计层次开发为角度视图,每个模块部件设计可分为3个角度视图设计,例如正视图、侧视图和顶视图,即图中角度视图1~角度视图3;第3个设计层次开发为物理属性,每个角度视图设计可细分为具体的物理属性设计,例如材质、色彩、造型、纹理等,即图中灰色方块所表示部分。其中,实线箭头所指部分表示作为上一级的一部分,虚线箭头表示所指双方具有相似性。

图1 基于CHD的产品概念设计方案划分框架
1.2 PFS理论
PFS理论[18]作为直觉模糊集(Intuitionistic fuzzy sets,IFS)[19]的一种推广形式引起了广泛学者们的关注并迅速发展。例如,赵晓冬等[20]将PT 和消去与选择转换法(ELECTRE)相结合,提出了一种用于解决已知属性权重、以毕达哥拉斯犹豫模糊不确定语言变量表达属性值的多属性决策方法;Akram 和Ali[21]介绍了两种新颖的混合模型概念,即毕达哥拉斯模糊双软集模型和粗毕达哥拉斯模糊双软集模型;Fei 和Deng[22]根据决策矩阵的毕达哥拉斯模糊信息,提出了一种基于相似性测度以及毕达哥拉斯模糊数(Pythagorean fuzzy number,PFN)和区间值毕达哥拉斯模糊数(Interval-valued pythagorean fuzzy number,IVPFN)的聚合算子新方法,能够有效地解决标准解权重赋予过程中的强主观性问题;Rani等[23]为解决决策专家和标准权重完全未知情况下可持续合作方的选择问题,提出了一种基于PFS和顺序偏好技术计算与理想解决概念方案相似性的方法。由上可知,PFS可以很好地解决产品概念设计中,决策专家和设计准则权重完全未知情况的多属性决策问题。
令X 为一给定的论域,则称三元组A={<x,µA(x),vA(x)>| x ∈X}为 PFS,其 中µA:X →[0,1],vA:X →[0,1]为 X 上 的模 糊集,µA(x),vA(x)分 别为X 上元素x 对A的隶属度和非隶属度,且∀x ∈X,µA(x),vA(x)∈[0,1], µ2A(x)+v2A(x)≤1, 那么πA(x)=为其犹豫度或不确定程度。
采用PFS的几何特性计算决策专家的权重分配值,设A是由模糊数 µA, vA, πA转 换的直角三角形坐标集合分别为直角三角形的3个坐标顶点。为TA和UA在Y 轴上的距离,为UA和VA在X轴上的距离,如图2所示。

图2 模糊数直角三角形A
通过计算A的几何中心点为
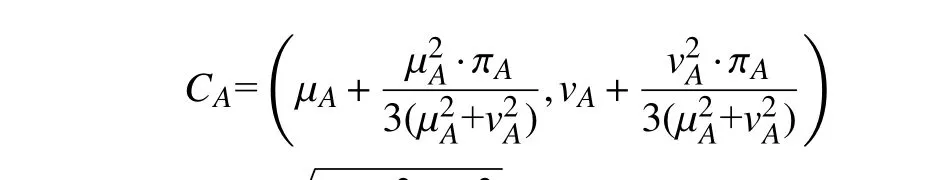
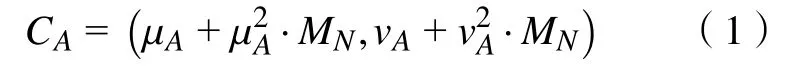
设a和b分别为A和B在论域X={x1,x2,···,xn}上的两个PFN,a =〈µA(xi),vA(xi)〉 ,b =〈µB(xi),vB(xi)〉,其中 xi∈X, 1 ≤i ≤n,则a和b的距离定义为
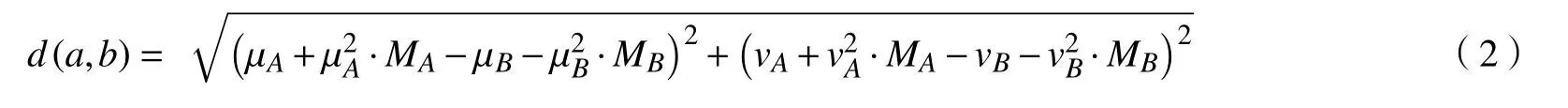
如图3所示为a 和b距离的几何意义,d (a,b)∈[0,1]。

图3 模糊数直角三角形A和B
1.3 PT方法
在实际的产品概念设计多属性决策过程中往往面临着更复杂的问题。例如,决策者偏好的模糊性、不确定性及非理性心理等因素对最终决策结果输出具有较大影响。故在毕达哥拉斯模糊环境下结合PT 方法对决策者的权重进行客观、合理的分配。
由于决策者在面对收益和损失时,存在风险厌恶和风险偏好等“有限理性”现象。因此,Kahneman和Tversky[24]提出了PT 和累积前景理论(Cumulative prospect theory,CPT)。在PT 中,价值函数和决策权重函数共同确定前景价值W
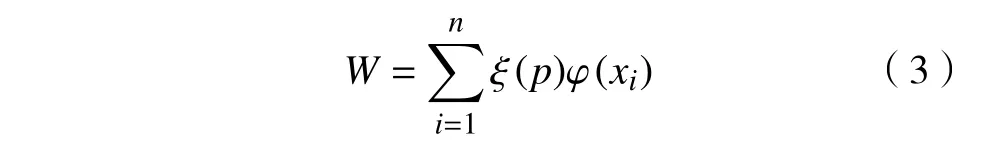
前景价值函数表示决策者在实际面对收益或损失时产生的主观感受价值,其原理可以通过不对称的S形函数描述,如图4所示。
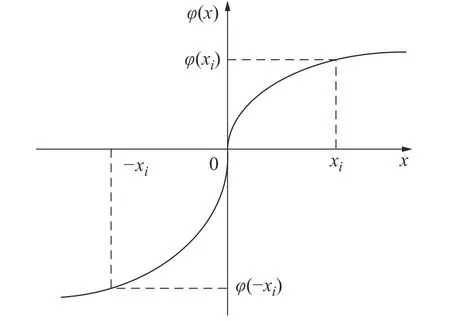
图4 PT 的价值函数
Tversky 和Kahneman[25]给出的价值函数φ(xi)幂函数表达形式如下:
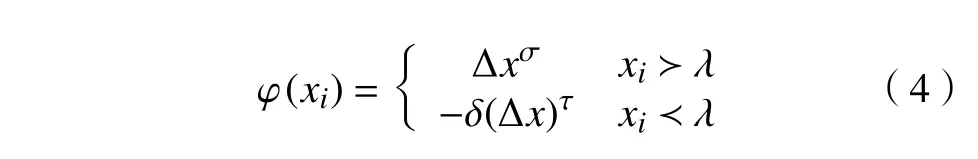
式中: Δx 为 xi偏 离参考点 λ的大小,且 xi≻λ 为 xi相比较于参考点 λ获得收益,xi≺λ 为 xi相比较于参考点λ遭受损失;风险系数 σ ∈[0,1],τ ∈[0,1]分别代表决策者对风险规避和风险偏好的程度, σ值越小,说明决策者在收益领域中更倾向于风险规避,类似地,τ的值越小,说明决策者在损失领域中更倾向于风险寻求,σ =τ=1表 示该决策者持中性风险态度; δ为损失规避系数,一般认为 δ>1,若此值越大,就表明相对于收益,损失对决策者会造成更大的心理波动。根据经验数据认为[26],通常取σ =τ=0.88,δ =2.25。
在决策权重函数ξ(p)中,收益概率权重函数ξ+(p)和 损失概率权重函数 ξ-(p)分别为:

式中:p为事件的发生概率;参数ε ∈[0,1],η ∈[0,1]分别为决策者在收益和损失时的态度,根据经验数据认为[27],通常取ε =0.61, η =0.69。
2 应用CHD的产品概念设计多属性决策方法
2.1 决策系统框架
如图5所示,建立了基于CHD的产品概念设计多属性决策框架,整个决策框架分为产品概念设计图像提取、产品概念设计相似性度量(Similarity measurement,SM)和产品概念设计多属性决策3个部分。
产品概念设计图像提取。根据图1提取所有备选方案的图像,得到整个备选方案数据集Z;划分为包括模块部件、角度视图和物理属性3个设计层次开发的集合Q。
产品概念设计相似性度量。使用余弦距离计算两个备选方案D1和D2的相似度;通过引入长度函数t1和深度函数t2分别计算D1和D2在3个设计层次的相似度。
产品概念设计多属性决策。基于上一部分可以得到k 个产品概念设计方案的决策矩阵。第i 个产品概念设计方案的决策矩阵 Ei包括k 个备选方案的3个设计层次相似度,第i 个产品概念设计方案的第j 个设计层次相似度aij需要获得m个决策专家在n个设计准则下进行概念评价的得分矩阵[r′ij]m×n;通过PFS和PT 相结合的方法得到各决策专家权重矩阵Gdes和设计准则权重矩阵 Hcri,进而得到得分矩阵 Ei;假定权重矩阵Xhie以获得每个备选方案的总体评价得分 Si,最终获得所有备选方案的总体评价得分的矩阵S 并进行备选方案排名。
其中,对于专家权重分配部分,假设N={N1, N2,···, Nm}为 决策专家集,A={A1, A2,···, An}为评价标准集,得到m ×n的决策矩阵S,将PFS转换为精确数得到评价标准权重向量λ ={λ1,..λ2,···,λn},选择正理想产品概念设计方案 A+和负理想产品概念设计方案 A-作为双参考对象,确定各决策专家的正理想解距离矩阵 D+和正理想解距离矩阵 D-,基于PT以正理想解 A+为参考点得到正前景效用价值函数 φ+(,以负理想解 A-为参考点得到负前景效用价值函数 φ-(通过分别计算收益概率权重函数ξ+(λj)和 损失概率权重函数 ξ-(λj),计算各决策专家前景价值 Wm,并从大到小排序进行归一化处理,得到各决策专家权重分配。
2.2 决策步骤
2.2.1 产品概念设计图像提取
对每个备选方案提取图像,整个备选方案数据集可以表示为

式中: xpicj,Di为产品概念设计方案图像picj在备选方 案Di的 权 重,xpicj,Di= freq∗num ,pic 为 基于CHD的产品概念设计方案的图像,总计l 张;D为备选方案,共k 个备选方案;freq 为出现相似图像的频率;num为出现相似图像的产品概念设计方案数量在总产品概念设计方案数量的占比,num=lg(p/K),p为出现相似图像的产品概念设计方案数,K 为总产品概念设计方案数量。
基于CHD的模块部件、角度视图、物理属性3个设计层次开发,整个备选方案数据集将被划分为如下3个子集。

式中: xpic1,mod为在模块部件级别中排序为第一个的图像的权重; xpic1,ang为在角度视图级别中排序为第一个的图像的权重; xpic1,phy为在物理属性级别中排序为第一个的图像的权重,而非同一张图片在3个设计层次开发中同时出现3次,即 xpic1,mod、 xpic1,ang、权重;为所有设计图像总数,=lmod+lang+lphy,xpic1,phy分别为不同的图像在3个设计层次开发中的lmod为模块部件级别的设计图像数, lang为角度视图级别的设计图像数, lphy为物理属性级别的设计图像数量,lmod、lang、lphy和均为正整数。
2.2.2 产品概念设计相似性度量
由于计算多属性准则之间的SM,需要分别对比3个不同设计级别的子集。因此,产品概念设计方案相似度的计算可以视为一个多维问题,则D1和D2的相似度可以表示为

在计算样本间的“距离(Distance)”时,需要选择合适的方法计算公式以得到正确的分类,故选用余弦距离计算两个备选方案D1和D2的图像相似度,即在模块部件级别中,备选方案D1和D2的余弦相似度计算为公式(1),其中, xpicp,mod,D1表示在模块部件级别中,产品概念设计方案D1中第p个图像的权重, xpicq,mod,D2表示在模块部件级别中,产品概念设计方案D2中第q 个图像的权重,通过类似方式,可以计算角度视图和物理属性级别的相似度。
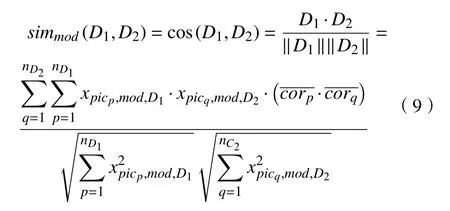

长度函数t1可以看作是谢泼德定律的扩展[28],在该定律中指数衰减函数是心理学中刺激泛化的普遍定律,可以通过层次结构中的路径跟踪来解决估计相关性的问题,则t1可定义为
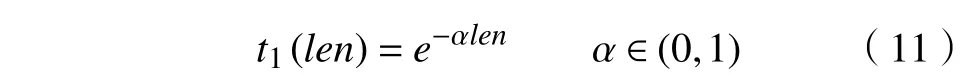
式中: α为介于0和1之间的实常数,当路径长度趋近于零时,t1将趋近于极限1,而路径长度无限增加,趋近于无穷大时,则t1将无限趋近于0。
由于不同深度的图像包含不同的信息性,即为,上层包含更多的常规信息,代表了产品更一般的轮廓,下层包含更多的细节描述信息,则深度函数t2可定义为
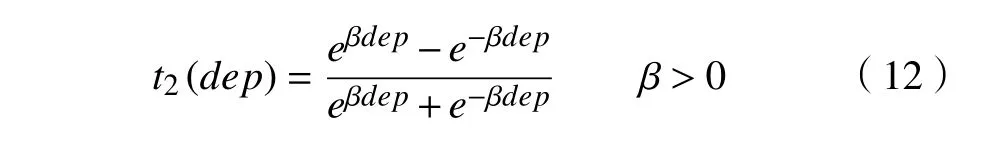
式中β 是平滑因子,且β>0。
总体产品概念设计方案相似度也应考虑CHD层次深度的影响,可以通过在三层上整合相似度来获得总体产品概念设计方案相似度,即

式中d epCHD为CDH 结构中根节点的深度。
2.2.3 产品概念设计多属性决策
对于总体决策矩阵E 代表了k 个概念,每个备选方案提取的图像都分为模块部件、角度视图、物理属性3个设计层次开发,并得到k 个产品概念设计方案的相似度比较矩阵。
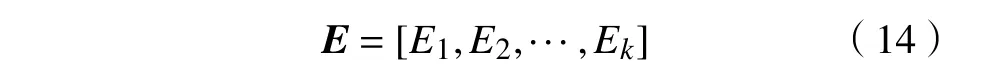
每个决策矩阵 Ei由具有3个设计层次的k 个备选方案的相似度组成,然而,对于每个备选方案的每个设计层次相似度aij并不是越大越好,可能存在aij数值大但并不符合实际决策中的多属性设计准则,因此,对于每个备选方案的每个设计层次相似度aij需要由多个决策专家在多个设计准则下进行概念评价,为决策矩阵 Ei的每个aij获得一个评分矩阵。其中,行代表m个决策专家,列代表n个设计准则。

由于每个决策专家在评价意见、背景经验和专业知识等多方面存在偏差,故需制定评级系统用以量化每个决策专家的权重以得到更加客观合理的评价结果。采用PFS和PT 相结合的方法(2.2.4中详细说明)得到各决策专家的权重矩阵 Gdes,从而实现客观合理的产品概念设计多属性决策。

然而,不同的设计项目在这些标准上可能具有不同的优先级,因此,通过类似的方法,得到设计准则权重矩阵 Hcri为
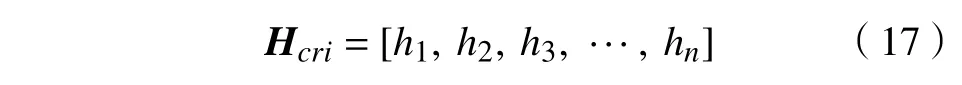
通过将决策专家权重矩阵 Gdes和设计准则权重矩阵 Hcri应用在评分矩阵上得到综合评估得分 rij为
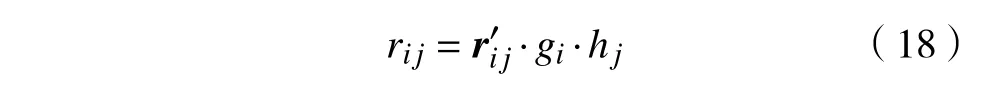
通过得到决策矩阵 Ei中每个相应元素aij的得分,可以得到与决策矩阵 Ei相对应的得分矩阵 Ei:

由于在实际的设计过程中,模块部件、角度视图、物理属性3个设计层次开发的设计重点可能有所不同。例如,部分产品概念设计项目期望得到更多物理属性上的相似度比较,而其他产品概念设计项目则更注重模块部件上的相似度对比。为了强调不同产品概念设计在CHD理论中不同层次开发中不断变化的设计侧重点,假定权重矩阵Xhie,并将其代入到评分矩阵 Ei中,以便获得每个备选方案的总体评价得分 Si。最后,可获得包含所有备选方案总体评价得分的矩阵S 及所有产品概念设计方案的排名。

2.2.4 应用PFS和PT 的决策专家权重分配
针对权重信息不完全确定的决策专家多属性权重分配的问题,采用一种将PFS几何距离和PT 相结合的方法。
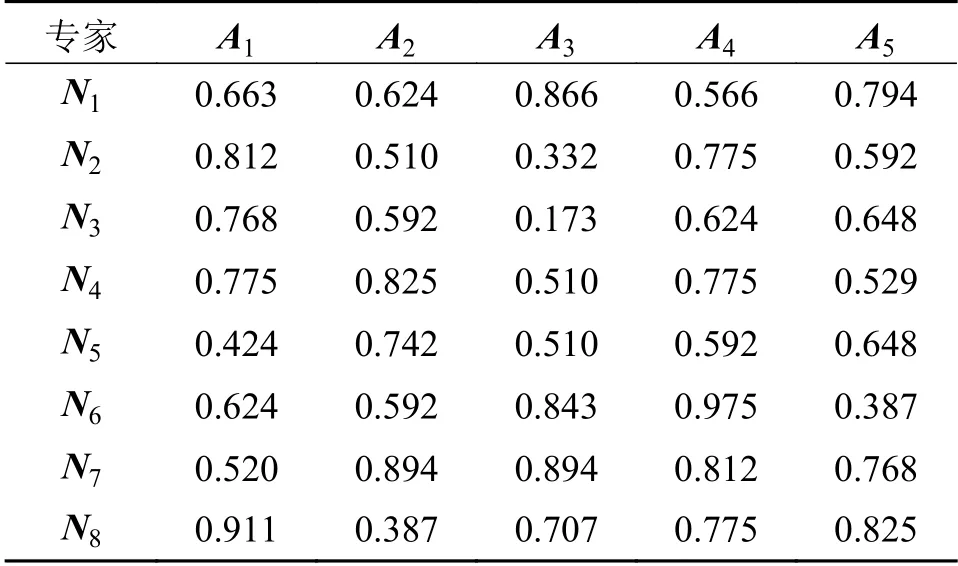
假设N={N1, N2,···, Nm}为决策专家集,A={A1, A2,···, An}是评价标准集。以PFN代表决策专家 Ni在 评价标准 Aj下的值,得到决策矩阵为:

步骤1计算各评价标准权重

根据Boran[29]等将直觉模糊数(Intuitionistic fuzzy number,IFN)转换为精确数的方法,定义评价标准 Aj的权重 λj计算公式,并得到评价标准权重向量λ={λ1,λ2,···,λn}
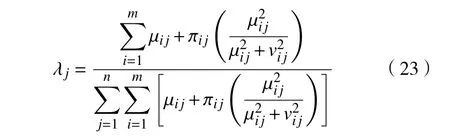
步骤2选择参考对象
由于对决策专家进行筛选排序时,看重的是每位决策专家在各项评价标准的优劣,因此,需要分别衡量决策专家预期与结果收益或损失的差距,以正负理想产品概念设计方案两种形式作为双参考解集。
设在正理想解集 A+=, A+2,···, A中,评价标准 A+j的正理想解计算公式为

则正理想解 A+j=〈µ+j,v+j〉的 π+j=π+j∈[0,1],1 ≤j ≤n 。
设在负理想解集 A-={A-1, A-2,···, A-n}中,评价标准 A-j的负理想解计算公式为
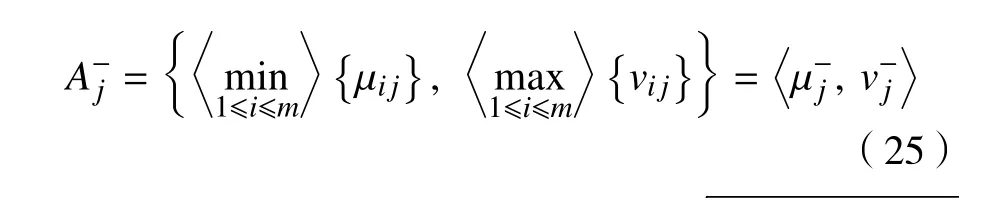
则负理想解 A-j=〈µ-j,v-j〉的π-j∈[0,1],1 ≤j ≤n 。
步骤3确定各决策专家的收益值和损失值
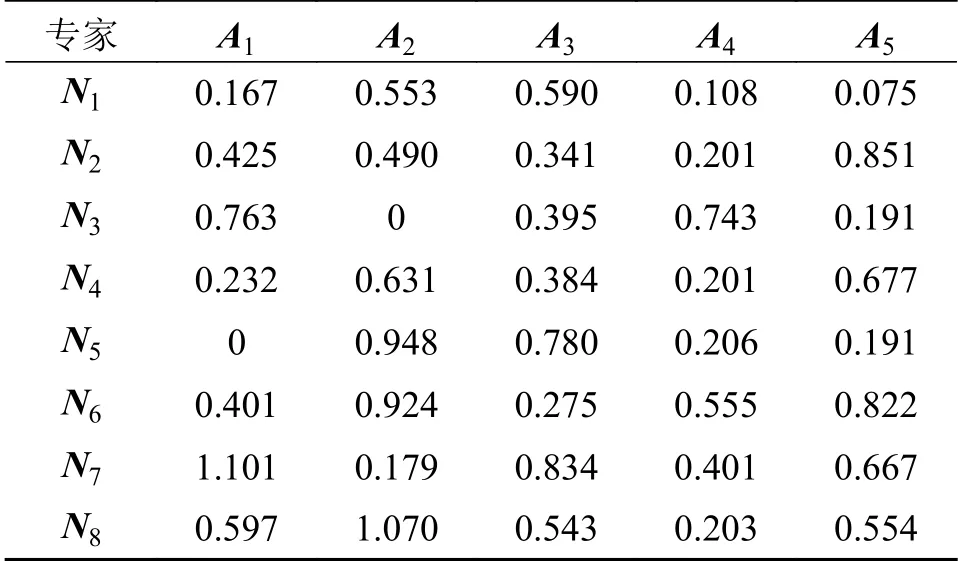
根据式(12)可以得到PFN sij=与正理想解 A+j的距离 di+j,获得正理想解距离矩阵 D+:
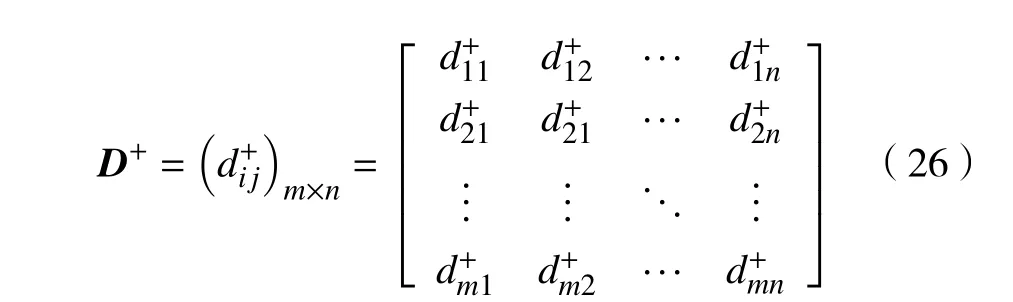
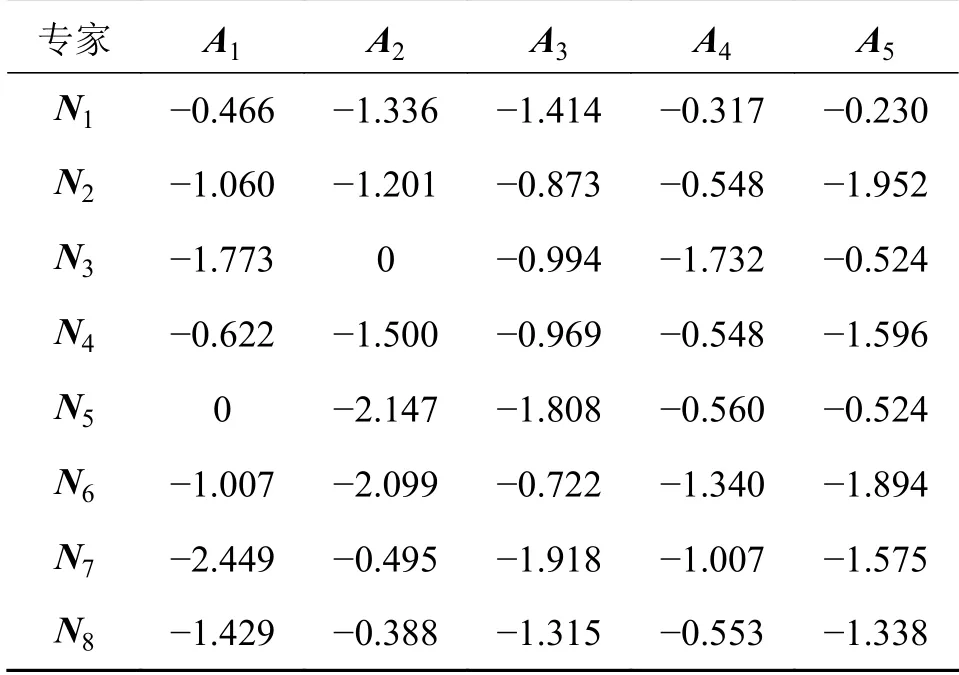
同理,得到PFN sij=与负理想解 A-j的距离,获得负理想解距离矩阵 D-:
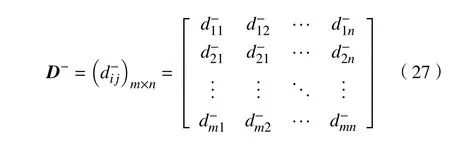
步骤4计算各决策专家PT 价值函数
根据式(19),将上述定义推广至毕达哥拉斯模糊环境,提出毕达哥拉斯模糊的前景价值函数:
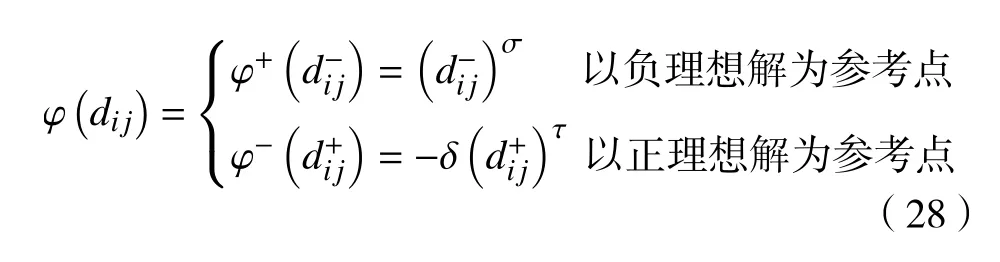
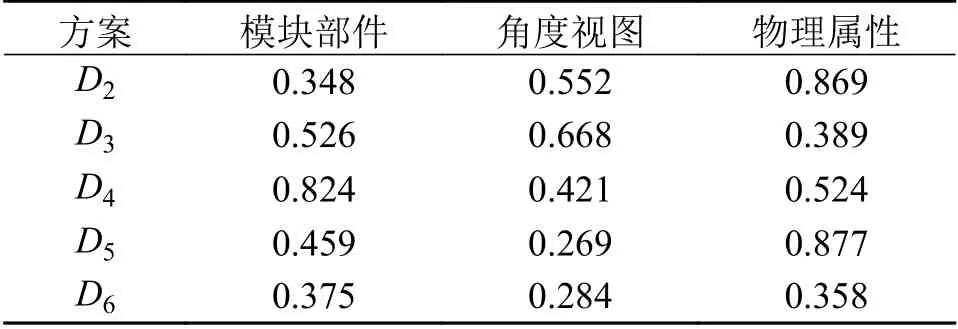
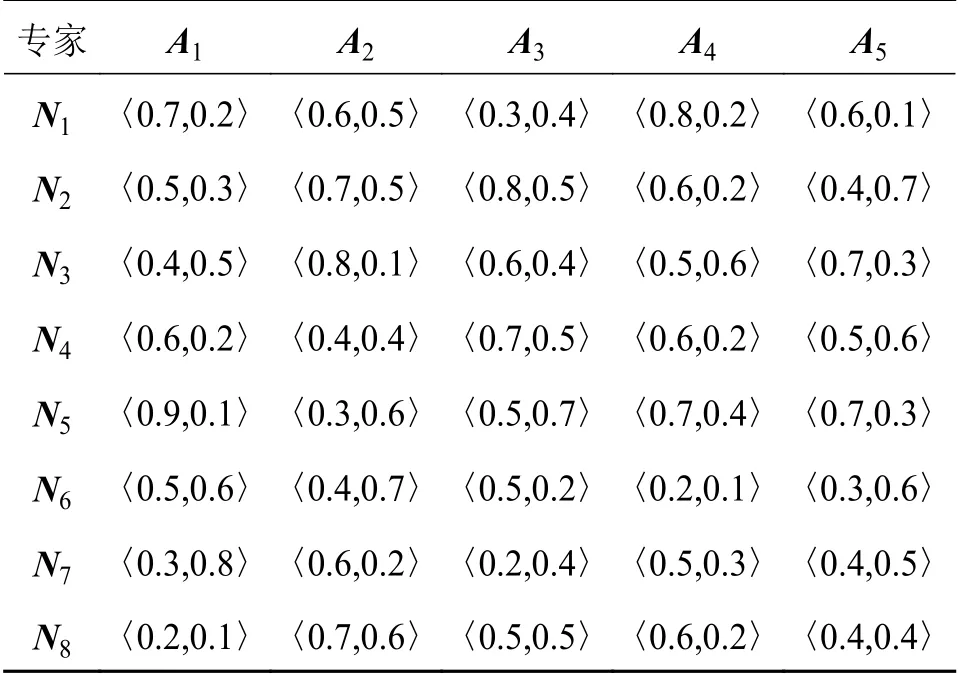
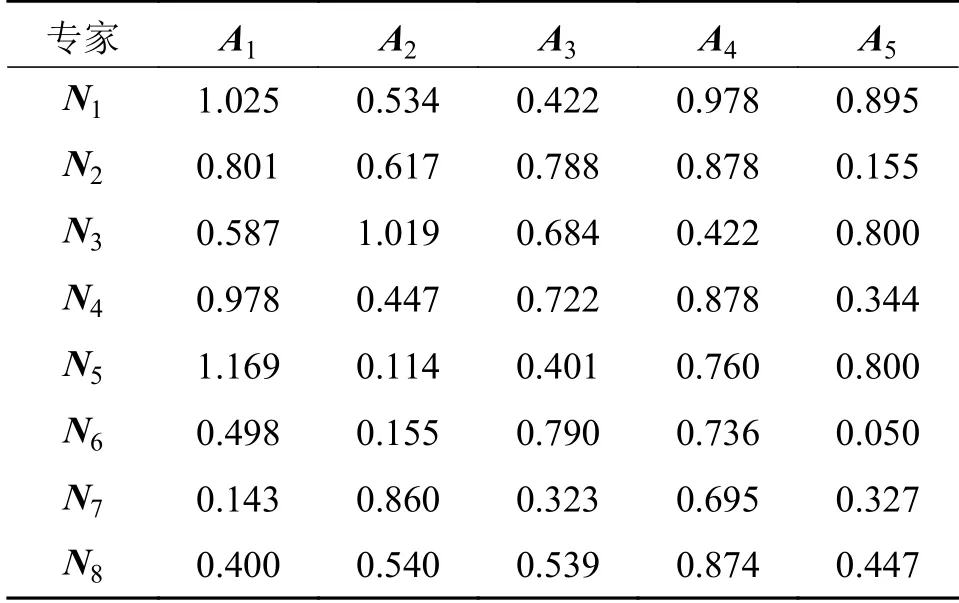
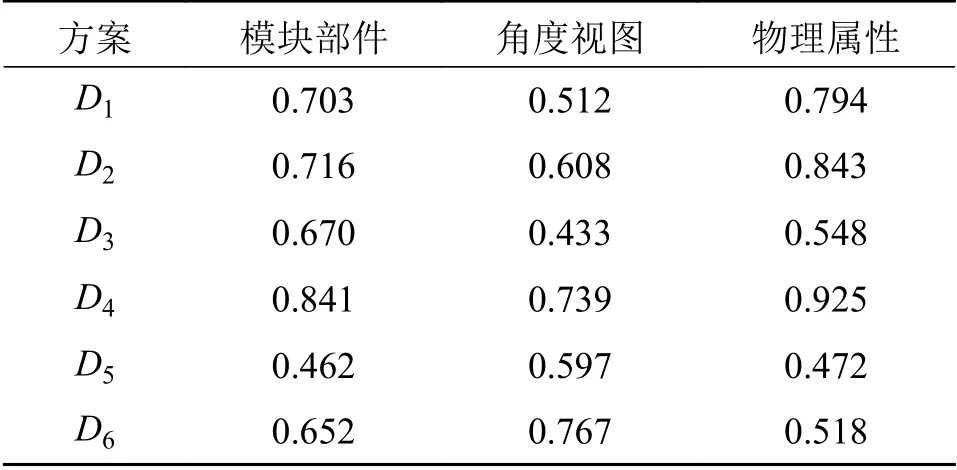
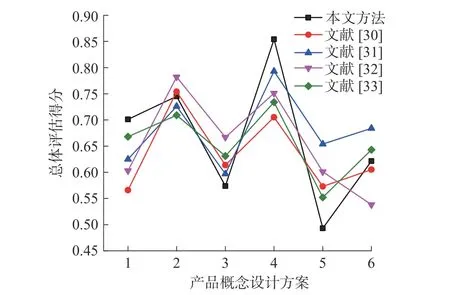
式中:若以负理想解 A-j为参考点,则 sij优于负理想解A-j,即 sij>A-j,将 D-代入 φ(Δx)=Δxσ,得到正前景效用价值函数;若以正理想解 A+j为参考点,那么 sij劣于负理想解 A+j,即 sij 步骤5计算各决策专家概率权重函数 将评价标准权重 λj代入至式(20)中分别得到收益概率权重函数ξ+和损失概率权重函数ξ-(λj): 步骤6计算各决策专家前景价值W 将式(28)、式(29)计算出来的价值函数和概率权重函数代入式(18)中,得到各决策专家前景价值Wm 步骤7计算各决策专家权重分配 将式(30)得到的所有决策专家前景价值 Wm并从大到小进行排序,若决策专家前景值越大,说明分配给该专家的权重应越大,最后,将所有决策专家前景价值 Wm进行标准化处理,得到各决策专家权重分配。 如图6所示,以6个响堂山佛像益智玩具的产品概念设计方案为例,基于CHD将产品概念设计方案图像分为模块部件、角度视图和物理属性3个设计层次开发。对于每个产品概念设计方案可分为佛头、佛身和背刻3个模块部件设计,每个模块部件设计可分为正视图、侧视图和顶视图3个角度视图设计,最后每个角度视图设计可根据具体产品概念设计方案图像所含内容分为材质、色彩、造型和纹理这4个物理属性设计。 图6 产品概念设计方案图像 基于上述方法,得到整个备选方案数据集Z,并划分为包含3个子集的集合Q。如表1所示,为响堂山佛像益智玩具方案1各图像的权重 xpicj,D1,由于物理属性权重层次篇幅过大,因此表1中仅显示佛头前视图设计层次的物理属性权重。 表1 产品概念设计方案1各图像权重 分别根据式(11)、式(12)得到长度函数t1和深度函数t2,并计算设计层次相关性代入至式(9)中,得到响堂山佛像益智玩具方案1与其他5个备选方案Di在3个设计层次的相似度决策矩阵 E1。如表2所示,同理求得 D2、 D3、 D4、 D5、 D6。 表2 5个备选方案相似度决策矩阵 将每个备选方案的每个设计层次相似度aij,由8个决策专家Ni在Y1成本、Y2实用性、Y3美观性、Y4可回收性、Y5可实现性、Y6预计寿命6个设计准则下进行概念评价,获得得分矩阵r′ij,对于响堂山佛像益智玩具方案1的第1个设计层次开发,即模块部件设计层次的得分矩阵如表3所示。 表3 方案1模块部件设计层次得分矩阵 通过2.2.4所提出的结合PFS几何距离和PT的决策专家权重分配方法计算各决策专家的权重矩阵 Gdes,对8个决策专家考虑A1受教育程度、A2工作经历、A3专业成果、A4专业技能、A5绩效成绩5个评价标准,利用PFS进行评价结果信息采集并构建评价矩阵,如表4所示。 表4 决策专家评价矩阵 计算过程分为以下7个步骤: 步骤1根据〈µij,vij〉计 算犹豫度πij=得到如表5所示的犹豫度矩阵。 表5 犹豫度矩阵 根据式(23),求出各评价标准权重 步骤2根据式(24)、式(25)求出各评价标准下的正理想解集A+和负理想解集A-: 步骤3根据式(2)分别计算评价矩阵和正理想解 A+j和负理想解 A-j的距离 dij,得到表6所示的正理想解距离矩阵 D+和表7所示的负理想解距离矩阵 D-。得到负前景值价值函数如表8 表6 正理想解距离矩阵 表7 负理想解距离矩阵 表8 负前景值价值函数 表9 正前景值价值函数 步骤5把步骤1中计算出来的各评价标准权重 λj代入式(29),得到收益概率权重函数ξ+和损失概率权重函数ξ-如表10所示。 表10 概率权重函数 步骤6把步骤4和步骤5计算出来的价值函数和决策权重函数代入式(30)中,得到各决策专家前景价值 步骤7最后,得到的所有决策专家前景价值Wm排 序结果为W1≻W2≻W3≻W5≻W4≻W8≻W6≻W7,并进行离差标准化处理,得到各决策专家权重分配为 同理,得到设计准则权重矩阵 根据式(18)将决策专家权重矩阵 Gdes和设计准则权重矩阵 Hcri代入表3的得分矩阵得到综合评价得分矩阵,进而得到aij和得分矩阵。如表11所示为6个响堂山佛像益智玩具的产品概念设计方案的3个设计层次开发的得分矩阵 Ei。 表11 总体产品概念设计方案3个设计层次开发得分矩阵 假定权重矩阵Xhie=[x1, x2, x3]T=[0.4,0.2,0.4]T。最终通过包含所有备选方案的总体评价得分的矩阵 S获得方案排序为D4≻D2≻D1≻D6≻D3≻D5,所以方案D4为最优方案。 一方面,由于本文基于CHD理论,并在决策专家及属性准则的权重分配中融合了PFS理论和PT理论,因此为了进一步说明所提出方法的优越性和有效性,选取文献[30-31]提出的决策方法进行对比分析,对于PFS和PT 理论选取文献[32-33]所提出的决策方法进行对比分析。考虑到在不同的决策方法中排序值量纲的不同可能会对排序结果造成不同的影响,因此对不同决策方法的总体评价得分进行归一化处理,并与本文决策结果进行对比,如图7所示。 图7 5种方法总体评价得分排序结果对比图 从图7可以看出,5种方法的排序结果大致相同,产品概念设计方案4和方案2的排序结果均在前两位,且明显优于其他产品概念设计方案,因此说明所提出方法的合理性。 一方面,在与CHD理论对比分析的决策方法中,由于产品概念设计方案5并未考虑产品开发过程中各备选方案的系统层级结构,因此对于产品具体特性及多样性等重要细节缺乏具体的指导原则和决策标准,故导致出现细节较少的获得较高评分的情况。另一方面,在与PFS和PT 理论对比分析的两个决策方法中,均出现了总体评价得分值非常接近的情况,例如在文献[32]中产品概念设计方案1和方案5的总体评价得分结果较为相近,在文献[33]中产品概念设计方案3和方案6的总体评价得分结果亦较为相近,因此无法判断某一方案是否绝对优于另一方。由于本文方法对于决策专家及属性准则的权重分配中考虑了犹豫度对隶属度和非隶属度的双重影响,使得最终方案结果存在明显的差异性,且各产品概念设计方案更具辨识度。 另一方面,将提出的包含PFS理论和PT方法的CHD模型与不含PFS理论和PT方法的CHD模型、PFS理论、IFS理论针对若干产品概念设计方案进行多轮最优产品概念设计方案多属性决策对比,决策误差和运算时间结果如表12所示。 表12 4种方法结果对比表 以决策误差进行结果对比,包含PFS理论和PT方法的CHD模型获得最小的决策误差5.61%,在不含PFS理论和PT 方法的CHD模型中决策误差略有上升,能够说明考虑PFS理论和PT方法能够提升CHD 模型的决策精度,有助于产品概念设计方案多属性决策问题的求解。另一方面,PFS理论和IFS理论决策误差均在10%以上,其原因为两种方法在备选方案的多属性评价标准中缺乏相似度比较,故各备选方案的评分需要单独计算,导致备选方案排名仅作为各评分属性的简单线性累加,缺乏整体而全面的综合相似度考量。以运算时间进行结果对比,PFS理论和IFS理论相对运算量较小,运算时间均在1.00 min 之内,对于所提出的CHD理论,由于需要计算各产品概念设计方案的相似度,运算过程及公式较为复杂,虽然降低了决策误差,但同时运算时间在一定程度上也略有增加。 针对多属性决策方法中存在各备选方案系统层级结构缺乏相互关系探索的问题,提出一种基于CHD的产品概念设计多属性决策方法。首先,定义了产品概念设计方案下CHD理论的应用方法,通过标准化的3个设计层次开发构建相似度比较矩阵,获得各备选方案的总体评价得分并进行排名。其次,在获得个备选方案总体评价得分的步骤中,通过引入PFS和PT 相结合的方法得到决策专家及属性准则的权重分配,该方法充分考虑了决策专家在面临真实决策情景下的风险态度。最后,通过响堂山佛像益智玩具的实例说明了该方法的科学性和可行性,为产品功能设计多属性决策方法提供了新思路。后续将在CHD理论上作出进一步的探索研究,如在多属性决策方法得到最优方案结论后,尝试对产品概念设计进行针对性指导;简化相似度对比步骤,提高运算时间,进一步优化、改进基于CHD理论的多属性决策方法,并尝试应用到其他领域的多属性决策问题中。
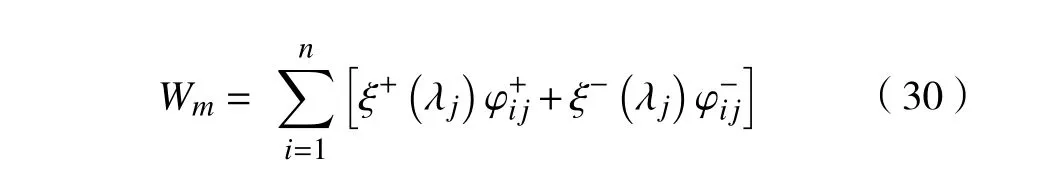
3 应用案例
3.1 案例分析与决策过程









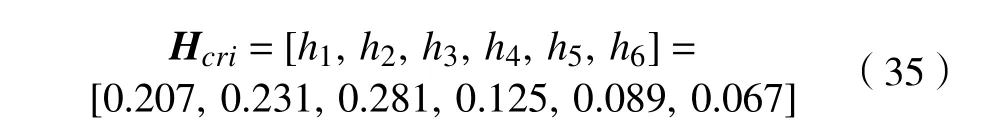
3.2 决策方法比较

4 结束语
