面向铝合金加工的GRA-SVM-CPSO混合多目标优化方法
2022-12-02庄可佳张服林代星翁剑
庄可佳,张服林,代星,翁剑
(1.武汉理工大学机电工程学院湖北省数字制造重点实验室,武汉 430070;2.华中科技大学机械科学与工程学院数字制造装备与技术国家重点实验室,武汉 430074)
铝合金因其密度小、韧性好、抗腐蚀能力强、质量轻等优越的机械性能,广泛运用于航空工业、汽车制造等领域。据统计,使用全铝发动机能降低汽车总重量10%,同时燃油经济效率可提高7%以上,能够更好地实现节能减排效果[1-2]。在实际生产加工铝制零部件时,如果以提高零件表面质量为目标,传统方法一般是操作工人根据自身丰富的加工经验,调整现有加工参数,但与此同时也会带来加工效率低下、刀具磨损严重等问题,而单纯以提高生产效率为目标,则会降低对零件质量的把控。
为解决加工品质与加工效率的矛盾,许多研究学者提出了各种优化方法,如响应曲面法(Response surface method,RSM)[3]、田口方法(Taguchi method)[4]和统计方法等,其中RSM因其简单普适性被广泛应用于各个领域。Azam 等[5]基于RSM设计了切削4340钢实验并分析了粗糙度和加工参数之间的关系,进一步指出进给率是影响加工表面质量的关键因素。Camposeco-Negrete[6]基于RSM 建立了6061铝合金切削过程能耗与粗糙度回归模型,Bagaber和Yusoff[7]基于RSM方法优化了316不锈钢切削过程的能耗和粗糙度。曾思峰等[8]利用RSM 方法建立了切削分力Fx和Fy的数学表达,并以最小化切削力为目标获得了切削铝合金变壁厚工件的加工参数。此外,基于田口实验方法优化切削加工过程也受到不少研究者的关注[9-11]。吴明明和周涛[12]利用田口实验法建立了L16正交阵列的模具钢铣削实验,结果表明加工表面粗糙度的主要影响因素是径向切削深度、径向切削深度与轴向切削深度相互作用。Tsao[13]将田口实验设计方法与灰色关联分析(GRA)相结合,改善了铝合金工件加工品质和减缓了铣削刀具磨损。Cica 等[14]基于田口方法设计了27组正交铣削硬钢的切削实验,然后利用GRA 方法选出切削性能较优的刀具涂层和加工参数,实现了低能耗、高效率、高品质的加工。
随着近些年人工智能技术的愈发成熟,越来越多的学者将其运用于加工优化系统,并取得了很多研究成果。莫蓉等[15]基于遗传算法优化神经网络的权值和阈值,准确地预测了加工过程中表面粗糙度。Xu 等[16]提出一种可用于预测钻削蠕墨铸铁过程中刀具磨损的自适应模糊神经系统(Adaptive neuro fuzzy inference system,ANFIS),在此基础上使用振动与通信粒子群优化优化算法(Vibration and communication particle swarm optimization, VCPSO)实现了高品质的加工。Gupta 和Guntuku[17]将ANN和SVM 作为遗传算法(Genetic algorithm,GA)的适应度函数模型,优选出了车削过程中表面质量最佳、刀具磨损最小和能耗最低的切削参数。Radovanović[18]分别采用迭代搜索(Iteration search)、GA 和多目标遗传算法(Multi-objective genetic algorithm, MOGA)这3种不同的方法优化了AISI1064钢的车削过程。
上述优化研究工作主要是先建立起参数与目标之间的关系模型,再使用优化算法对多目标进行优化求解,而在涉及到多目标问题时,需要建立多个目标的预测模型,其建模计算过程较为复杂,并且在不同目标之间相互冲突和影响时,难以选择合适的切削参数组合,因此本文以6061铝合金为研究对象,通过全因素实验方案设计,采用GRA 方法将多目标(切削力、表面粗糙度和材料去除率)转化为单目标问题(灰色关联度,GRG),建立了切削参数与灰色关联度之间的SVM模型,最后基于混沌粒子群算法(CPSO),以最小化切削力和表面粗糙度、最大化材料去除率为目标寻找出了铝合金加工的最优切削参数组合,并通过与PSO算法进行对比,发现CPSO算法具有更佳的全局寻优能力,能够在更快地达到全局最优位置。
1 实验与测量
为获得切削过程实验数据,以切削速度、进给速度和切削深度这3个切削参数作为实验变量,测量不同切削参数组合下的材料去除率、表面粗糙度和切削力。实验选用6061铝合金棒料作为工件材料,其各元素的质量分数与物理力学特性分别如表1和表2所示[19]。实验在数控系统为GSK 980TDS的数控车床上进行,使用刀具为方形硬质合金刀片,其型号为CNMG120404-BF,所使用刀柄型号为MCLNR-2525M-12;采用Kistler 9257B测力仪进行切削力数据采集,工件表面粗糙度的测量由Mar-Surf PS10完成,具体实验设计如图1所示。

图1 实验装置图

表1 6061铝合金各元素的质量分数%

表2 6061铝合金物理力学性能
根据刀具手册的推荐值,在极值范围内将切削变量分为3个水平,具体编码及水平如表3所示。由于涉及的变量较少,为保证实验数据的充分性,本实验采用全因素全水平实验设计,共设置27组不同切削参数组合的实验。

表3 切削参数的编码及水平
2 结果分析
针对切削过程的优化研究一般包含3个步骤:采集并处理实验数据、建立目标函数和寻找最优参数组合。本文所使用的多目标优化方法是一种联立GRA、SVM 和CPSO于一体的方法,其中GRA用于从实验数据中提取目标函数值,SVM用于建立切削参数与目标函数之间的映射关系,CPSO用于寻找最优参数组合,算法流程见图2。

图2 基于GRA-SVM-CPSO混合方法的多目标优化流程图
具体而言:首先,对实验的切削力(Fc)、表面粗糙度(Ra)和材料去除率(MRR)数据进行统计处理;其次,利用GRA 将多目标响应(Fc、Ra和MRR)转化为GRG 的单目标响应;再次,基于SVM建立切削加工参数与GRG 的关系模型;最后,利用CPSO寻找所设置的加工范围内最优的GRG 并进行验证实验。
2.1 实验结果
分别采集x 向、y 向和z 向切削力,然后计算切削合力Fc,即

每组切削实验完成后,使用粗糙度测量仪测量工件加工表面3个不同部位的粗糙度值Ra1,Ra2,Ra3,再求取平均值作为这组实验的零件表面粗糙度值Ra,即

加工过程材料去除率MRR可以表示为

根据式(1)~ 式(3)可以得到如表4所示的实验结果。
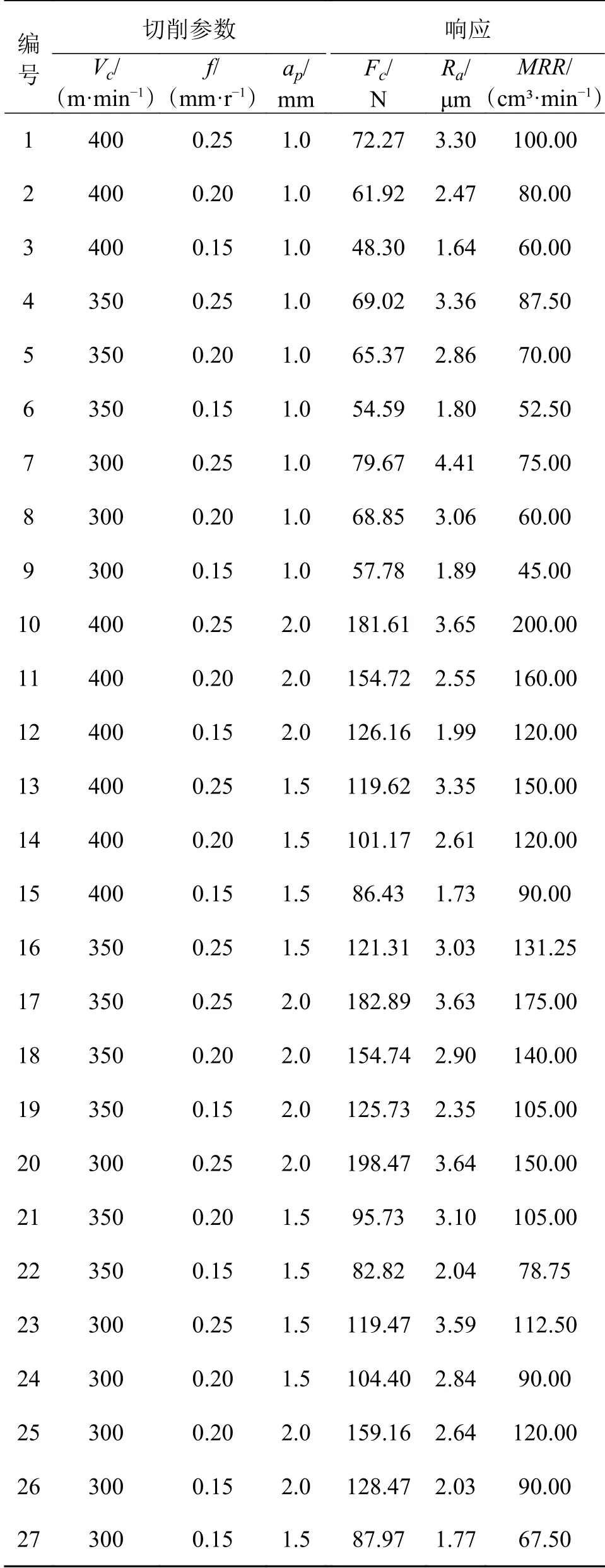
表4 实验数据
2.2 灰色关联分析(GRA)
GRA 方法致力于通过从现有数据中生成、挖掘和提取有用的信息来研究具有部分已知信息的不确定系统[20]。基于灰色关联分析在解决多目标响应方面的优越性,建立起加工参数与灰色关联度之间的关系模型,将多目标问题转化为单目标问题。灰色关联分析的步骤如下[21]:
步骤1原始数据归一化。在多目标问题的研究中,由于不同的目标变量具有不同的单位和数量级,因此需要对数据进行归一化处理。令(k)和分别表示原始数据序列和比较序列,i=1,2,···,m(m表示试验次数),k=1,2,···,n(n表示响应变量数),在本文中,m=27,n=3。根据原始序列特性的不同,归一化的方法也不一样,对于“越大越好”特性的序列,如材料去除率MRR,归一化变换公式为
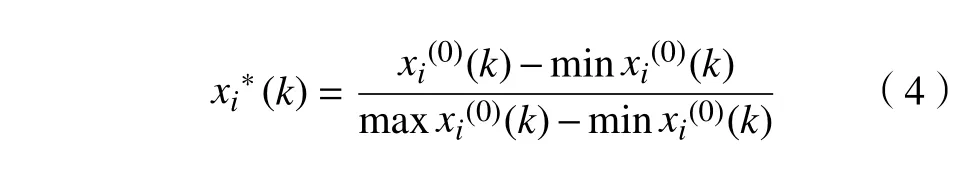
对于“越小越好”特性的序列,如切削力Fc和表面粗糙度Ra,其归一化变化方法可表示为
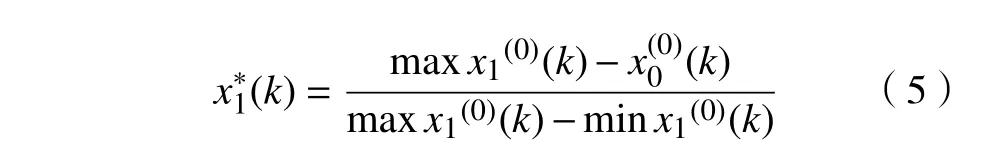
步骤2灰色关联系数计算。在对原始序列进行归一化处理之后,灰色关联系数(取值范围为(0,1])计算方法为

式中: γ(x∗0(k),x∗i(k))为灰色关联系数, x∗0(k)为参考序列, x∗i(k)为 比较序列;Δ0i(k)为偏差序列。
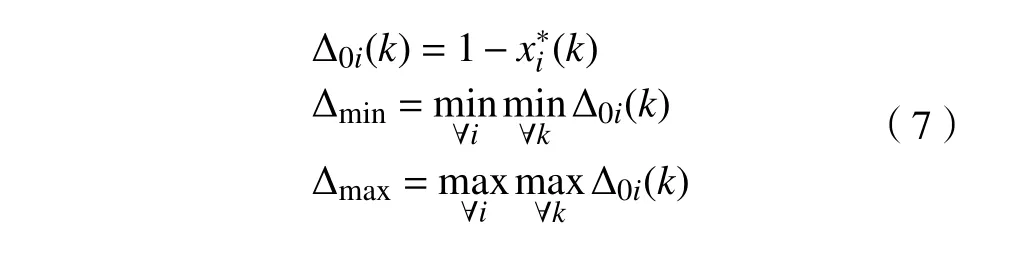
式中ξ 为分辨系数,ξ ∈[0,1],本文取ξ =0.5。
步骤3灰色关联度计算。基于灰色关联度系数加权求和,其定义公式为

式中 βk为第k 个响应目标的权重值,其权重值反映了对应指标在整个指标中所占的比重,=1。在本文中,表面粗糙度Ra和材料去除率MRR这两个最终指标相比于过程指标切削力Fc更加重要,因此将切削力Fc的权重设置为0.2,加工表面粗糙度Ra和材料去除率MRR设置为0.4。
基于上述的GRA 可以得到如表5所示的灰色关联系数和灰色关联度。
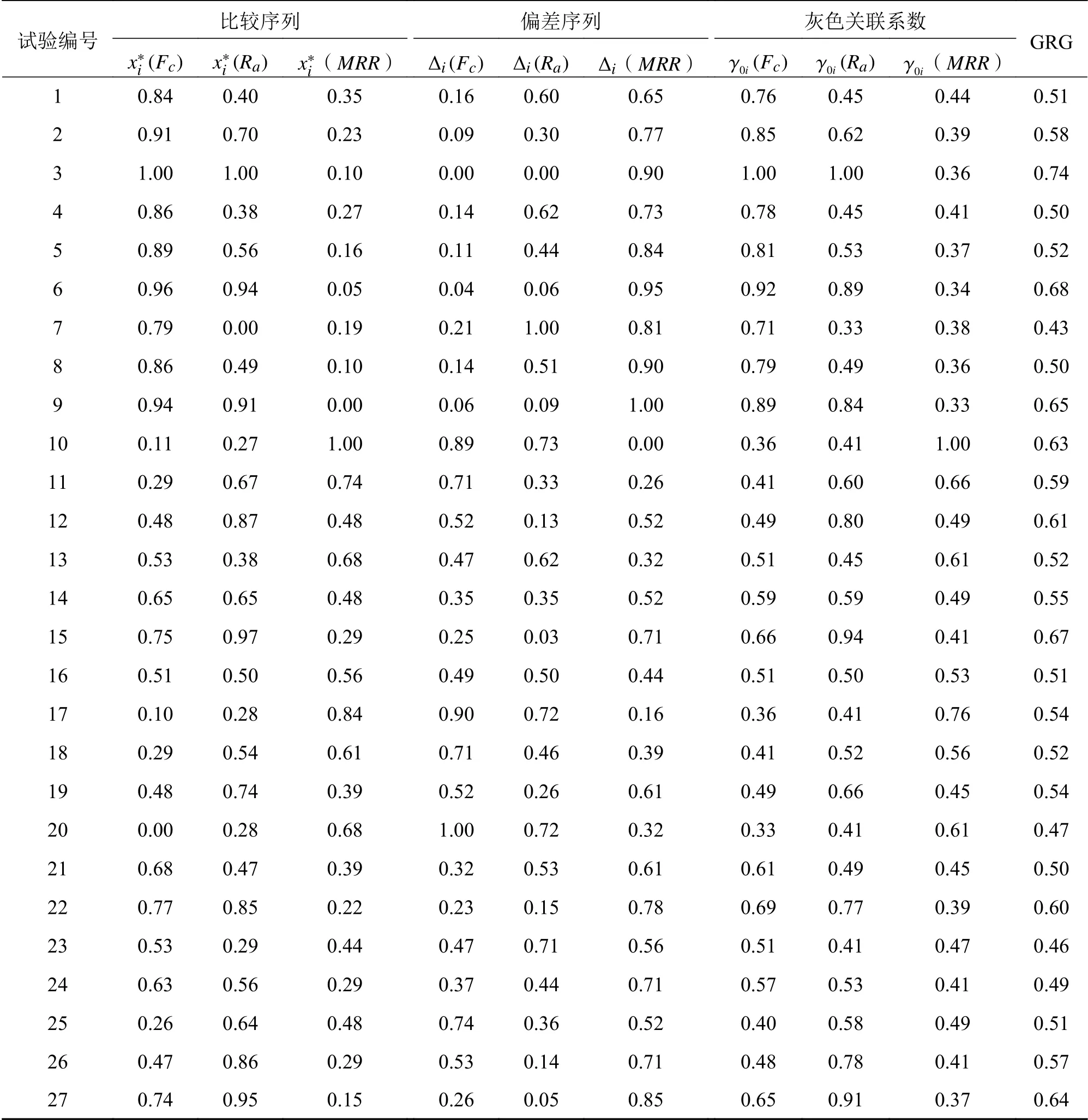
表5 灰色关联系数和灰色关联度
2.3 支持向量机回归模型(SVM)
SVM是一种用于建立输入和输出之间映射关系的机器学习方法,具有良好的泛化性能,能够较好地解决小样本、非线性和高维数据等实际问题,适合用于小样本数据下的结果预测[22]。本文将切削参数作为SVM模型输入,将2.2节计算得到的GRG作为模型的输出。在27组实验数据中,随机选取22组数据作为模型的训练样本,并将剩余的5组数据作为模型测试样本。以上过程可通过LIBSVM[23]工具箱实现,选用的核函数是径向基核函数(RBF),需要确定模型中的两个参数c 和g。基于训练均方差经过初次训练SVM模型粗选得到的系数c 和g 最优值分别为11和-3.5,精选得到的最优值分别为10.97和-3.85,本文中训练和测试的GRG 预测效果如图3所示,训练误差和测试误差如图4所示。
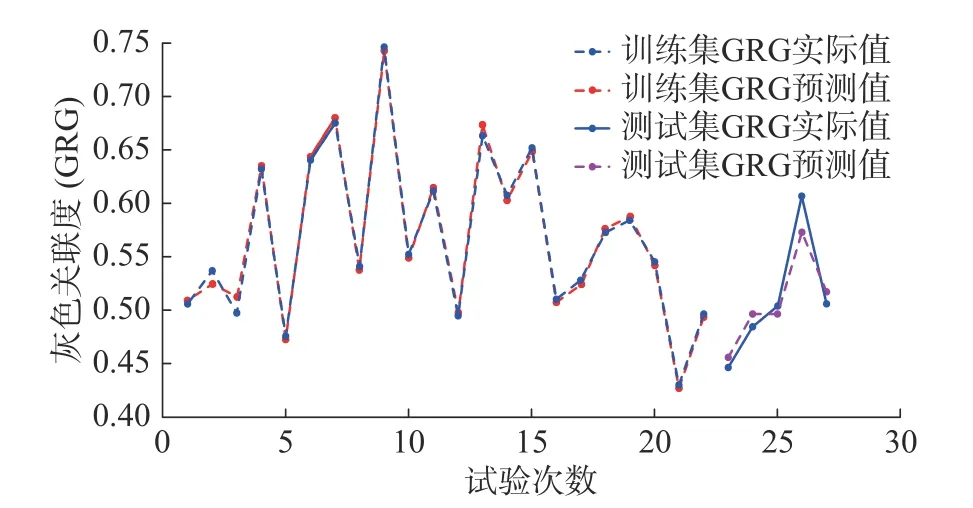
图3 SVM 预测效果
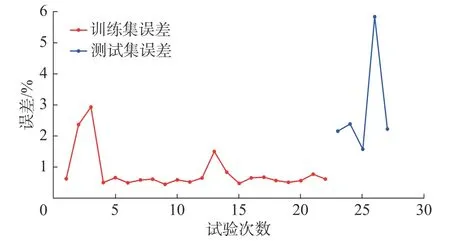
图4 SVM 预测误差
从图3可以看出,SVM模型在训练样本集和测试样本集上的灰色关联度预测值与实际灰色关联度值相差较小。从误差折线图上(图4)可以看到,测试集最大误差不超过6%,训练样本集上的平均误差为0.83%,测试集样本上的平均误差为2.84%,由此可知SVM具有很高的预测精度。
2.4 混沌粒子群算法优化(CPSO)
PSO是一种现代启发式算法,因其较强的鲁棒性、快速收敛性和稳定性得到了较为广泛的运用[24-25],但PSO算法具有进化后期收敛速度较慢、在解决复杂的非线性问题时可能陷入局部极值等缺点[26]。为了克服PSO算法的这些缺陷,本文采用更优的CPSO算法,相对于原始PSO算法,该算法添加了混沌操作,增强了算法全局寻优的能力。其基本思想是以PSO算法的流程为主体流程,当粒子陷入局部最优值时,利用混沌搜索技术引导粒子快速跳出局部最优,加快收敛速度,具体的算法流程[27]如下:
步骤1初始化参数。参数的初始化主要包含两部分:1)PSO的参数设置,2)混沌搜索算法的参数设置,具体如表6所示。

表6 参数设置
步骤2初始化粒子速度和位置。依据所设定的粒子位置和速度边界随机产生一群带有位置和速度特征的粒子。
步骤3评价粒子群。以所建立的SVM 预测模型作为PSO算法的评价函数,以每个粒子的位置作为模型输入变量,以模型输出值作为粒子适应度值,更新粒子群个体极值Pi和全局极值Pg。
步骤4判断是否进行混沌搜索。计算粒子群平均粒子D 和适应度方差σ2,其计算方法为:

式中:N 为粒子群规模;L为搜索空间对角最大长度;m为解空间的维数,本文中解空间维数为3;POSid为第i 个粒子第d 维坐标值;为所有粒子第d 维坐标值均值;fi为粒子i 的适应度值;favg为粒子群的平均适应度值;f 为归一化标定标因子,其作用是限制 σ2的大小。D 值的大小直接反映种群的密集程度,D 越大表明种群越分散; σ2直接反映了个体聚集程度,其值越大表明聚集程度小。
如果D<α或者σ2<β,则表明粒子群陷入局部最优值,需要进行混沌搜索跳出局部最优,转至步骤5,否则转至步骤6。
步骤5混沌搜索。先随机产生一混沌变量Y0,再利用式(11)产生混沌序列Yn,并将其映射到粒子群位置范围区间 Yn′,直至混沌迭代次数n>M,再利用混沌搜索得到最好的可行点Y*,将其随机取代粒子群中的一个粒子,然后转至步骤6。
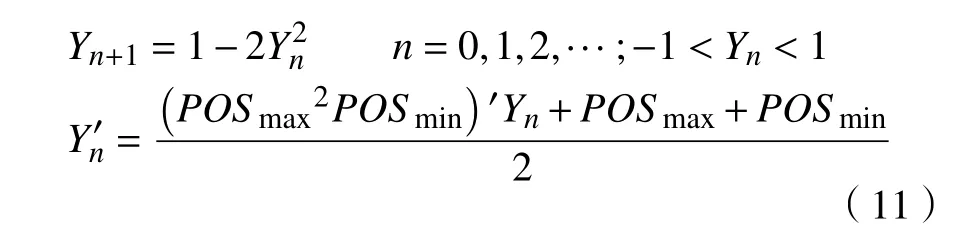
步骤6判断迭代次数t<Tmax,如果是则转至步骤7,否则转至步骤8。
步骤7更新权重、粒子的速度和位置,并转至步骤3。
权重更新公式为
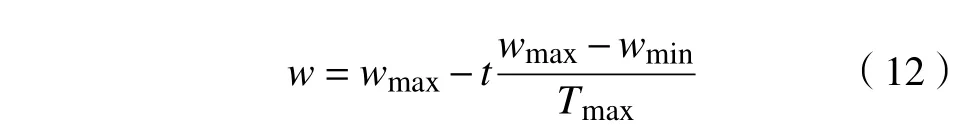
粒子的速度更新公式为
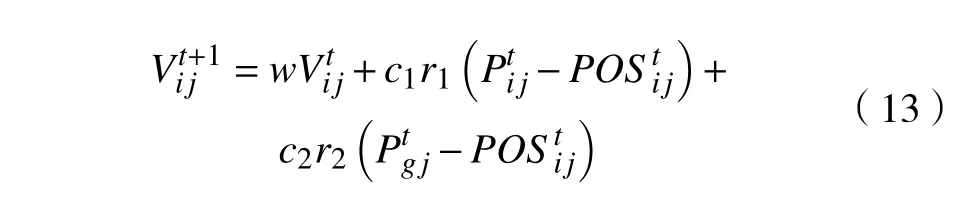
粒子的位置更新公式为
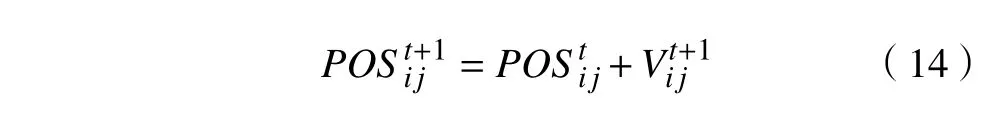
步骤8 粒子群进化过程结束,返回全局最优解。
基于CPSO的优化算法得到的最大灰色关联度值迭代曲线如图5所示,在切削速度Vc=400 m/min,进给速度f =0.15 mm/r,切削深度ap=1.0 mm 时最大灰色关联度值为0.745 8,与第4组实验中的灰色关联度0.74相差不大,表明在该切削参数下切削铝合金的切削性能最佳。为了验证CPSO的优越性,在相同参数下使用PSO对最佳灰色关联度值进行迭代寻找,结果表明使用PSO寻优得到的最佳灰色关联度值与CPSO的相同,均为0.745 8,此时的切削参数组合为:切削速度Vc=400 m/min,进给速度f =0.15 mm/r,切削深度ap=1.0 mm。为了对比CPSO与PSO的寻优能力,在相同参数下分别使用这两种算法进行迭代寻优5次,求取5次每代的种群最佳灰色关联度值的均值作为该算法的最佳适应度值,其迭代曲线图如图5所示,结果表明CPSO算法平均在第15代就已经收敛至全局最优值,而PSO算法平在第42代才收敛至全局最优值,这就说明CPSO算法相比于PSO算法,其全局搜索能力更强,能够更快地找出最佳粒子位置。
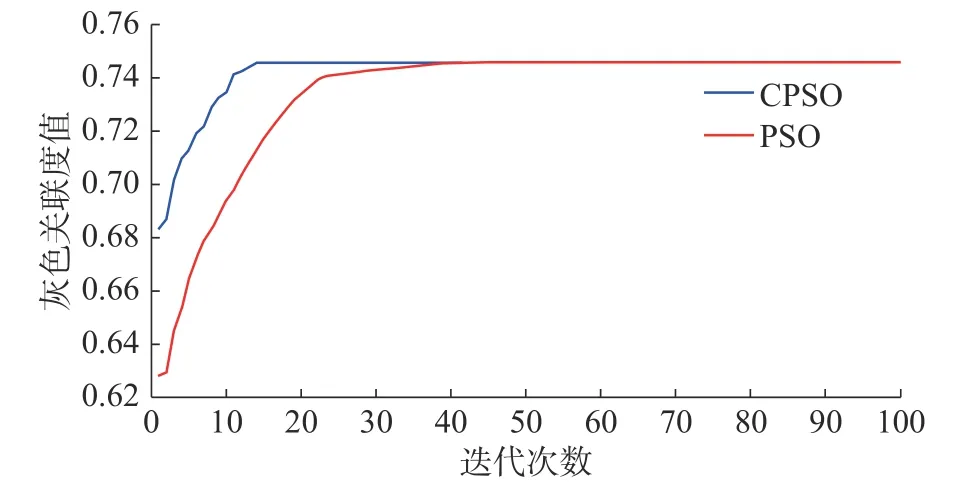
图5 CPSO与PSO迭代曲线图
3 结论
本文以铝合金切削为研究对象,建立了一种GRA-SVM-CPSO混合的多目标优化方法,解决了铝合金加工过程中多目标参数优化问题。基于以上研究过程,本文的主要结论可总结为:
1)使用GRA 的方法将切削力、表面粗糙度和材料去除率的多目标优化问题转化为GRG 的单目标问题,解决了多目标优化过程不同目标矛盾冲突的问题。
2)基于SVM 模型建立了切削参数与GRG之间的关系模型,通过随机实验分析结果表明该模型具有良好的预测性能。
3)基于CPSO和PSO优化得到的最优切削参数组合为切削速度400 m/min,进给速度0.15 mm/r,切深1 mm,有效改善了铝合金切削过程的切削力和表面粗糙度。对比表明,CPSO具有更强的全局搜索能力,能够更快地找出全局粒子的最佳位置。
