大尺寸表面喷涂的交界区涂层均匀性分析

王毅，王国磊，李波，闫继宇，路敦民*,

（1.北京林业大学工学院，北京 100083；2.清华大学机械工程系，北京 100084；3.中国航空工业集团公司济南特种结构研究所，济南 250023）

涂层厚度均匀性是机器人表面喷涂质量考核的重要指标之一。对大尺寸产品表面进行机器人喷涂时，采用面片划分以化繁为简是一种常用的做法。而面片交界区域的涂层厚度，是整体喷涂厚度均匀性的主要影响因素。

在离线编程中对涂层均匀性的控制很大程度上依赖于合理的涂层厚度分布模型。根据许多研究者的理论，涂层厚度分布模型通常被划分为两类：一类为无限模型，如高斯分布模型、柯西分布模型；另一类为有限模型，如抛物线模型[1]、贝塔模型[2-3]、双贝塔模型[4]、多变量模型[5]等。而目前使用较为广泛的双贝塔模型认为在喷涂区域内，沿底面椭圆长短轴方向均服从贝塔分布[6-7]，缺乏对喷涂起始和终止区域涂层厚度分布的数学描述。

基于对面片交界区涂层厚度控制的问题，本文在椭圆双贝塔模型的基础上提出了一种对喷涂起始与终止区域进行描述的涂层厚度分布模型，并基于此模型理论分析和实验验证了交界区域的影响因素。

1 问题描述

对大尺寸工件进行喷涂时（以大面积板材为例，见图1），通常将工件表面划分为若干个小型面片以便于机器人作业[8-9]。在每个小面片上喷涂时，喷涂轨迹会采用“Z”字型轨迹[7]。图1中，轨迹A1至轨迹A8为左侧A面“Z”字型喷涂轨迹，轨迹B1至轨迹B8为右侧B面“Z”字型喷涂轨迹。其中喷枪底面椭圆在A、B 两面轨迹起始、终止位置重叠的部分称为面片交界区；重叠部分长度在喷炬底面短轴长度中所占的比率称为横向搭接率。

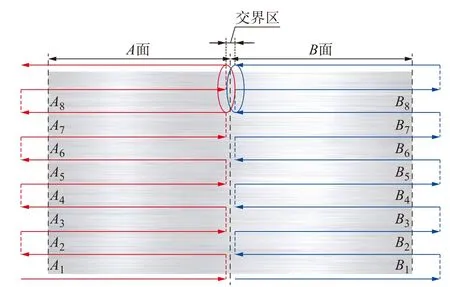
图1 大面积铝板喷涂轨迹

理论而言，只要保证交界区喷涂轨迹处处连续即可保证涂层厚度均匀，但是事实上按照图1中的轨迹进行喷涂会导致A、B两面交界区涂层厚度偏厚且不均匀，如图2所示，其原因通常在于机器人喷枪自身结构[10]。一般机器人所用空气喷枪自身结构如图3所示，其开枪工作原理为：压缩空气从进气口进入到喷枪内部，达到一定压力后克服弹簧的阻力将喷针顶起，涂料而后从喷针和喷嘴的环形缝隙通过；关枪工作原理为压缩空气低于一定压力后弹簧阻力将喷针压回，阻塞涂料流出。

图2 横向搭接率为1时喷涂实物照片及厚度曲线图

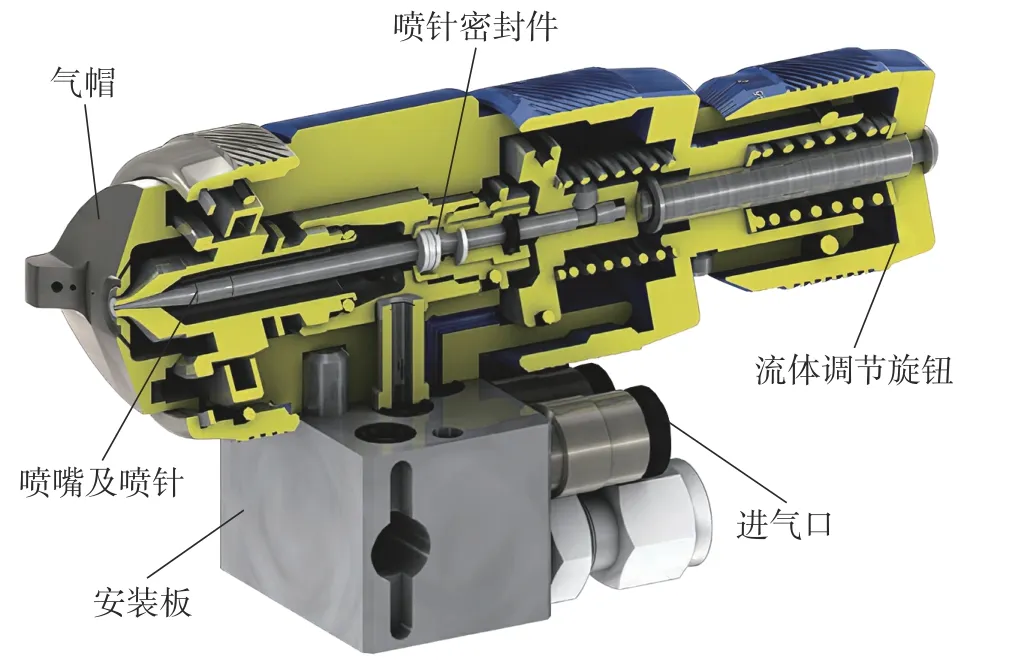
图3 机器人空气喷枪结构爆炸图

由于空气具有可压缩性，且开关枪的压缩空气管路有一定长度，故压缩空气达到压力的时间虽然很快，但仍然需要一定的时间，通常在0.2 s左右。因此，空气喷枪在开枪的短时间内存在一个流量陡增而后趋于稳定的过程，而关枪时流量会陡增后渐熄。这种现象导致了如果按照横向搭接率为1进行喷涂，面片交界区的涂层厚度会偏厚，甚至导致流挂。

工程上为了解决这个问题，一般通过设置一定的横向搭接率来有效降低搭接区域的涂层厚度，减少不均匀性，但是这个距离目前主要依靠实验手段来确定，缺乏理论和定量的分析。因此，本文引入了喷枪模型理论，通过对交界区的涂层厚度进行理论分析以确定最优的横向搭接率。

2 喷枪模型分析与改进

2.1 椭圆双贝塔模型

图4所示的椭圆双贝塔喷枪模型是一种喷炬底面为椭圆形区域的涂层厚度分布函数，广泛应用于建立喷枪模型中。该模型认为在喷枪定点喷涂时，喷涂区域底面为一个标准椭圆，分别沿椭圆长轴和短轴方向，涂层厚度均服从贝塔分布。

对于底面椭圆区域内任意一点(x,y)，其对应的厚度值D 满足

式中： Dmax为 喷枪模型内厚度的最大值； a为椭圆的半长轴长度； b为椭圆的半短轴长度； β1为长轴方向上的贝塔值； β2为 短轴方向上的贝塔值。其中 β1与β2不必一致，但在平行于长轴（或短轴）方向的不同截断面上，其贝塔值需保持一致。

根据文献[4]可知，在喷枪模型满足条件β1=β2=2的情况下，喷枪在匀速直线喷涂作业时，垂直其移动方向任意截面上厚度服从

式中v 为匀速直线移动速度。

2.2 对喷涂起始与终止区域进行描述的椭圆双贝塔模型

如图5所示，对于平板匀速直行喷涂而言，中间区域 S2厚度通常保持的较为均匀；在喷涂起始区域S1和 终止区域S3，其厚度相较于中间区域偏高且不均。

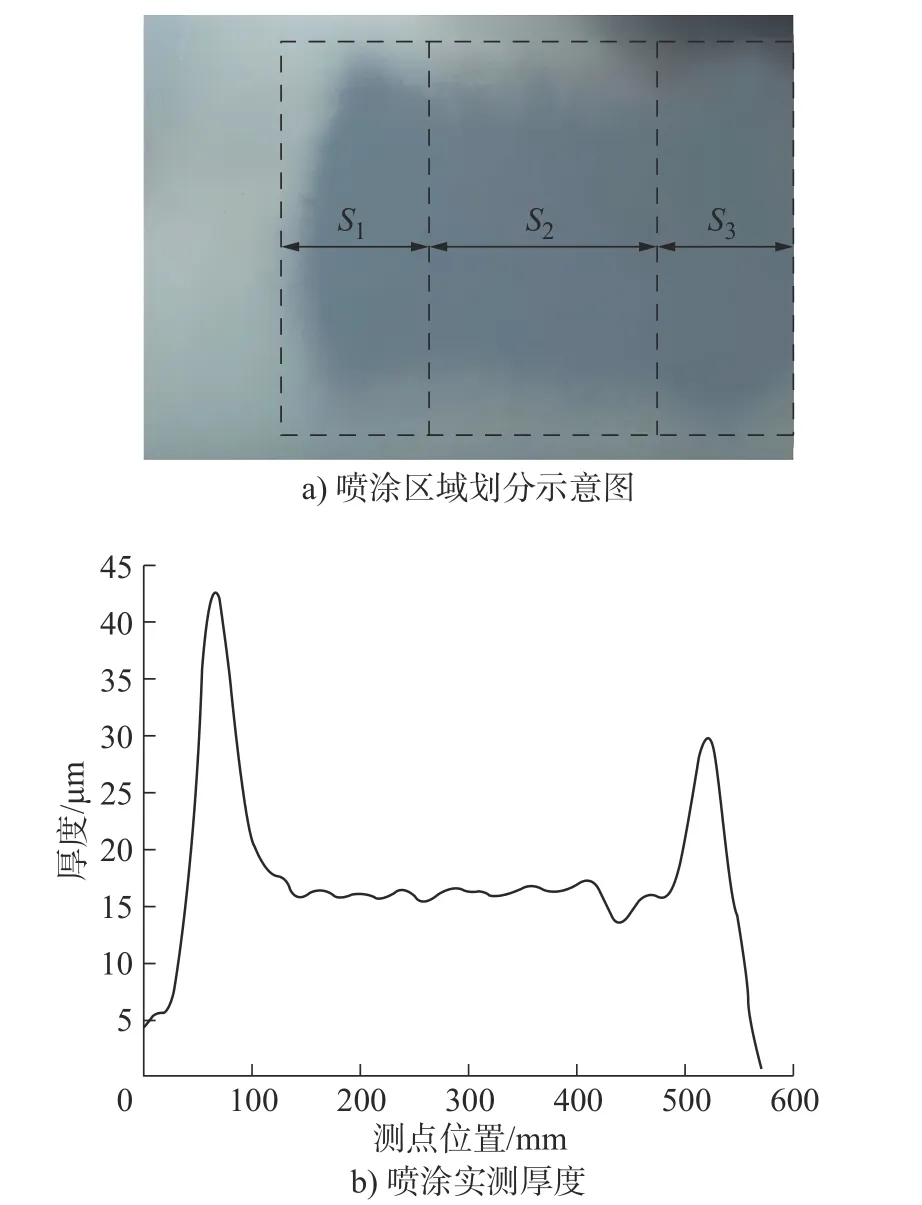
图5 喷涂区域划分示意图及对应厚度曲线图

在喷涂区域内，喷枪模型内部任意一点厚度均为该点在被喷炬扫掠过程中涂层不断积累的结果[5]；而压缩空气及喷枪结构对流量造成的影响一般可以通过涂层最大厚度Dmax来表征。故而求取合理的喷枪模型，即是求取一个合理的Dmax- x 函数。

通过大量喷涂实验数据拟合，得到了如图6所示的Dmax- x 曲线。其中， D1为喷涂起始陡增达到的涂层厚度， D2为 稳定时的涂层厚度， D3为喷涂终止陡增达到的涂层厚度； x1为喷涂起始到达到稳定所经过的距离， x2为喷涂过程中关枪前所经过的距离， x3为喷涂过程从开枪至关枪所经过的总距离。

图6 D max - x 模型

由图6可知：在0-x1位置内，涂层厚度先陡增至最大值 D1再 逐渐回落，达到稳定值 D2； 在 x1-x2位置内，涂层厚度处于稳定值 D2； 在 x2-x3位置内，涂层厚度先陡增至 D3而后渐渐降低至零。对图6曲线进行拟合，得到各个参数及涂层厚度函数表达式分别为：

式中： a1和 b1分别为左侧二次曲线的二次项系数和一次项系数； a2、 b2和c分别为右侧二次曲线的二次项系数、一次项系数和常数项系数。

3 横向搭接率分析与最优值区间求解

3.1 横向搭接厚度分布函数

在对大型产品进行面片切分完毕后，每一个面片的喷涂起始区域与下一个面片的喷涂终止区域互相连接[11-12]。如上文所述，由于喷枪自身结构和气控影响，每一道轨迹的喷涂起始和终止区域相较于中间区域会显得不均，在实际工程中面片之间会采用横向的搭接率 k来调整面片交界区长度以使得厚度相对而言更为均匀。

在横向搭接率为0时，两面片交界区截面厚度曲线如图7所示。左侧部分为某个面片喷涂终止处厚度曲线，右侧为与其相接邻面片喷涂起始处厚度曲线。交界区总长度 x1+x3-x2；为简化计算，假定有x3-x2=x1。

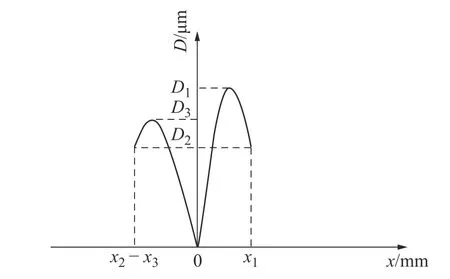
图7 横向搭接率为0时交界区厚度曲线图

若两面片之间采用横向搭接率进行厚度修正，结果如图8所示。

图8 使用横向搭接率修正后交界区厚度曲线图

两者之间重叠区域长度为 x1+x3-x2，则有交界区的参数和厚度分布函数分别为：

3.2 影响因子 D1/D3分析

本文以涂层厚度标准差来表征涂层在某区域内的均匀性。对式（9）中 x在 ( -x1,x1-kx1)区间内，控制D2、 D3保 持不变，以 D1/D3为影响因子对涂层厚度均匀性与横向搭接率之间的关系进行分析。

通常而言，横向搭接率取值区间为0～1；当横向搭接率处于1～ 2的区间内时，交界区涂层厚度分布曲线如图9所示。

图9 横向搭接率处于1～ 2区间内交接区厚度曲线图

虽然该交界区域内涂层厚度均匀性有所提升，但交界区涂层厚度值会显著上升，易出现流挂等现象；在搭接率系数大于2时，厚度会出现波峰-均匀-波峰的现象，在涂装生产中，此现象被称为“斑马线”，为涂层瑕疵的一种。因此在正常喷涂作业时，搭接系数通常选取在0～ 1范围内。

利用MATLAB，在影响因子处于1～3的不同区间内，对式（9）进行离散化取点，得到每个点所对应的厚度值，而后计算在不同搭接率下离散点集在总体区间下的标准差，得到如图10所示的曲线。

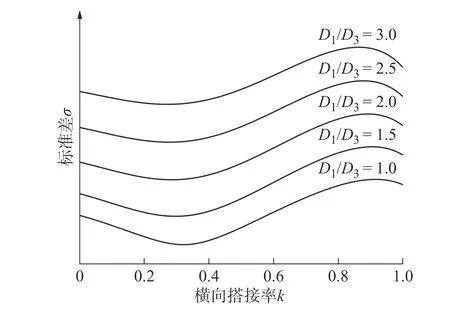
kσ图10不同D1/D3值下- 曲线

由图10可知，标准差随搭接率 k上升而呈现先下降后上升的趋势，对于不同的 D1/D3因子，其呈现的规律性并无变化。因而可以得到结论，对于横向搭接而言，搭接率k 的最佳取值空间为0.2～ 0.4。

3.3 影响因子 D2/D1分析

对式（9）中 x在 区间(-x1,x1-kx1)内，控制 D1、D3保 持不变，以 D2/D1作为影响因子进行分析。

随着 D2/D1数值趋近于1，涂层厚度分布函数曲线逐渐趋向于梯形曲线，与文中所论述的曲线相异；当 D2/D1趋近于0时，涂层厚度分布函数中间部分厚度趋近于0，无实际应用价值。故而仅分析 D2/D1处于0.3～0.6区间内，涂层厚度标准差与影响因子之间的关系。

利用MATLAB，在影响因子处于不同区间内，对式（9）进行离散化取点，得到每个点所对应的厚度值，而后计算在不同搭接率下离散点集在总体区间下的标准差，最终得到如图11所示曲线。

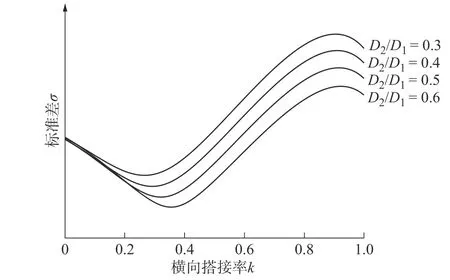
kσ图11不同D2/D1值下- 曲线

由图11可知，横向搭接率最优取值随影响因子D2/D1而逐渐增大，但仍处于0.2 ～ 0.4区间内。

4 实验验证

4.1 实验原料及装置

某型脂肪族涂料；3 mm 厚铝板；采用ABB IRB5400型喷涂机器人携带美国DEVILBISS AGMD514型机器人喷枪进行喷涂实验；涂层厚度测量设备采用德国EPK MiniTest730测厚仪。

4.2 椭圆双贝塔喷枪模型拟合

如上文所述，在喷枪匀速直线移动时，其移动方向任意截断面上任意一点厚度应符合式（2）的数学模型。为验证椭圆双贝塔模型的准确性，设计如下实验：令喷枪垂直于待喷涂工件表面并保持姿态不变，以400 mm/s的速度在铝板上匀速直线喷涂；期间保持喷涂参数如表1所示。在测量时，以1 cm 为单位沿长轴方向逐点测量，每个点位测量3组数据取均值；为消除测量误差，同时在多个长轴截断面重复测量，将x 值相同的点位的数据求平均值作为测量数据。

表1 喷涂参数

图12 测量点与理论模型比照

4.3 厚度分布函数参数标定

为验证修正模型准确性，设计实验如下：换用另一较长的铝制试验样板，其长度应能保证喷枪开枪与关枪位置均在铝板上；令喷枪垂直于待喷涂工件表面并保持姿态不变，采用如表1所示喷涂参数，在铝板上从左至右进行匀速直线喷涂。测量时，沿喷涂机器人匀速移动方向，在椭圆中心线取点，以1 cm 为间距逐点测厚。

通过数据处理可得到Dmax- x 模型中的各个参（D1，D2，D3，x1，x2，x3）计算后可获取式（3）中的参数（a1，b1，a2，b2，c），各参数如表2所示，拟合结果如图13所示。

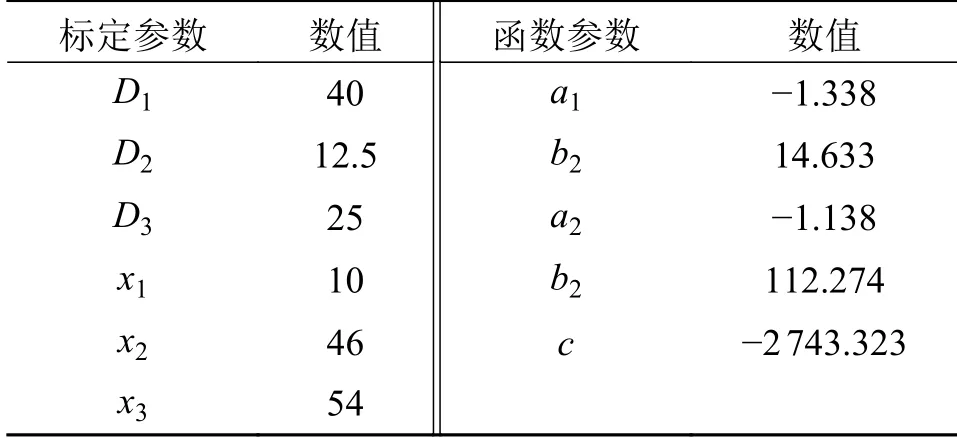
表2 厚度分布函数标定参数

图13 测量点与理论模型比照

经计算验证，测量数据与理论模型平均偏差为1.1μm，最大偏差不超过4 μm，证明了模型的准确性。

4.4 横向搭接率验证

为验证横向搭接率与标准差之间关系是否与图10相吻合，设计5组对照实验如下：更换试验铝板，保证实验时参数与表1中相同；而后操作机器人喷枪从铝板左侧开始喷涂，行进至铝板中间处后，关枪终止喷涂；接下来沿移动方向继续移动一定距离，该距离需使得搭接率分别满足0、1/3、1/2、2/3、1；达到位置后，开始喷涂，行进一定距离后关枪终止喷涂。测量并计算在不同横向搭接率下交界区厚度标准差如表3所示。

表3 横向搭接率-标准差数据

在本实验中， D1/D3=1.24。将表3中数据代回图10中曲线，最终结果如图14所示。可见曲线与实际测量结果相吻合，标准差在0.3～0.4达到最低值为正确结论。

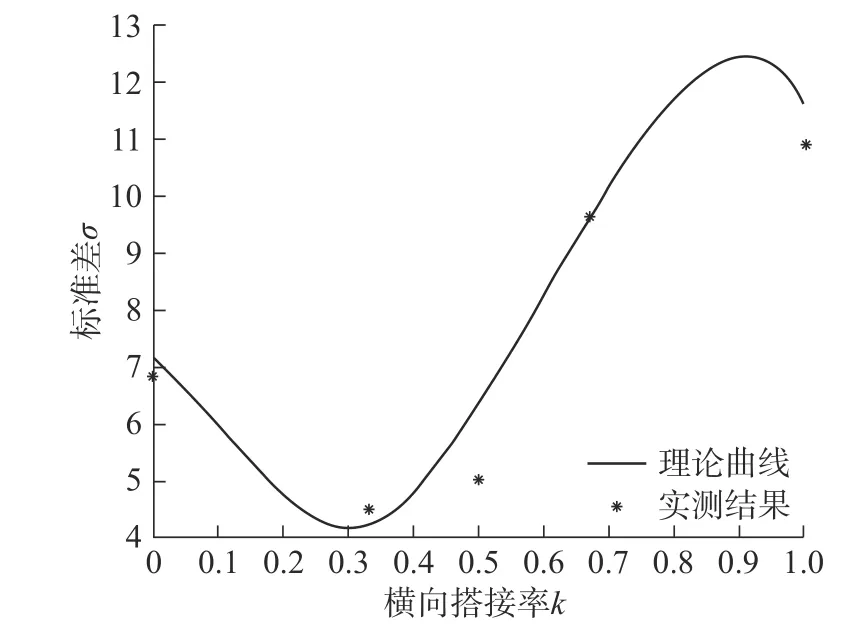
图14 实测数据与理论值对照图

5 工程应用

5.1 工程应用概述

在其他喷涂条件（如：气源、喷枪、涂料等）不变的情况下，喷涂轨迹对于喷涂质量而言显得尤为重要。尽管多数厂家对轨迹设计都提出了自己的适用标准，但对于细节调试，尤其是面片交界区，大曲率拐角处则格外依赖于技术人员的相关经验和轨迹设计水准[13-14]。

对于大尺寸产品外表面喷涂而言，技术人员通常会根据机械臂及喷枪到达能力来将产品外表面划分为若干面片[15]；在一般情况下，面片交界区的质量难于控制和保证，因此会在面片划分时尽量减少面片数量以减少交界区数量[16-17]。对于大型柱体类产品而言，其面片通常为2～ 4个。以某壁管类产品为例，其面片划分为2个，仿真环境搭建如图15所示。该类产品轨迹设计规划后为仿形的绕柱曲线，对于管壁外表面上任意一点处涂层厚度，可通过喷枪模型来加以预测。对于面片交界区等厚度不均处，可提前改变轨迹来加以优化。

图15 壁管类产品仿真环境

5.2 面向大型罩体类产品应用

基于如上理论和实验验证，将本文所论述的方法在工程实际中加以应用。

原有某大型罩体产品外表面需进行喷涂，在离线编程时受机械臂活动空间制约将产品划分为4个面片。在未采用横向搭接率优化前（原搭接率为1），4个面片交界区极易出现过厚导致垂边、流挂等现象。与根据修正后双贝塔喷枪模型预测结果吻合。

在对交界区喷涂轨迹进行优化时，首先于平板上进行涂层厚度分布函数参数标定获得开关枪处最大厚度以及其对应的x 值，从而根据参数搭建喷枪模型。而后根据本文结论，横向搭接率采用0.3～0.4之间以获得最优的厚度均匀性。最后将交界区原本重合起始、终止点，向远离面片交界线的方向上位移相应距离，以此实现优化。

对于本例中原有横向搭接区域总长在200 mm左右时，选取目标交界区长度为80 mm。在离线编程时，体现为两面片起始与终止喷涂点沿面片交界线两侧各移动60 mm 距离。优化后效果如图16所示，交界区厚度处于工艺规程所指定的范围内（D ± 15%，D 为目标厚度），实现优化目的。

图16 优化后交界区

6 结束语

本文首先对大尺寸工件喷涂交界区问题成因进行了分析，而后对椭圆双贝塔喷枪模型进行了分析，针对双贝塔模型对于喷涂起始、终止位置缺乏描述的问题提出了新型模型。进而对横向搭接率 k与涂层厚度标准差进行了讨论与数学最优区间求解，从而得到了最优的 k值区间为0.2～0.4。之后通过实验验证了以上模型与最优值区间的正确性有效性，从而使喷涂机器人在喷涂作业中能够更有效的调整面片间搭接率距离，提高喷涂质量和喷涂效率。

未来的研究中，必要的工作有两部分：1）对于不同的喷涂设备与气控系统，其喷涂厚度分布模型也会有所不同，所以应该设计并提出更有普适性的厚度分布函数；2）在喷涂过程中，由于机器人在加速和减速过程中会产生一定的延滞，这往往会使得喷涂起始与终止区域厚度过高，一般人工喷涂时会采用“漂枪”动作加以调节，因而应该建立完善的“漂枪”动作喷涂厚度模型，以便对实际机器人生产作业进行把控。