橡胶四元件模型动力学特性分析

俞力洋，黄然，吴少培，丁旺才，李国芳，屈鸣鹤

（兰州交通大学机电工程学院，兰州 730070）

橡胶业作为国民经济重要基础产业之一，不仅为人们提供日常生活不可或缺的日用、医用等轻工业橡胶产品，而且向交通、建筑、机械、电子等重工业及新兴产业提供各种橡胶部件[1]。更具体地，橡胶材料极佳的可塑性、优越的超弹黏弹性及良好的阻尼特性，使其在承受交变载荷时能耗散大量振动能量，因而通常被用作隔振减震器核心部件，如橡胶衬套[2]、车辆座椅缓冲垫[3]、轨道车辆用弹性橡胶垫[4]、空气弹簧橡胶囊[5]等。

早期人们通常采用简单Kelvin-Voigt 模型（弹簧与阻尼并联）或Maxwell模型（弹簧与阻尼串联）模拟包括橡胶在内的各种隔振吸振系统的动态特性[6-7]。但后来学者们发现Kelvin-Voigt 模型与Maxwell 模型均无法同时反映橡胶材料的松弛特性与蠕变特性[8]，因此目前常通过增加模型耦合程度或引入非线性因素以提升模型准确度，如Zener 模型[9]、Burgers 模型[10]、Berg 模型[11]、Dzierek 模型[12]及分数导数模型[13]。值得注意的是，虽然引入新元件或增加元件数目可从一定程度上增加模型精度，但这同时也加大了系统的求解难度。相比两元件模型与Zener 模型，四元件模型具有较少的系统参数及较低的计算难度，且其本身能够准确反映橡胶材料的松弛特性和蠕变特性，不失为开展橡胶隔振系统动力学特性分析的较佳模型。

目前对各种场景下橡胶等黏弹材料模型等效与静力学特性计算方面的研究已较为成熟，但对材料黏弹性模型复杂动力学行为的研究还有待进一步深入。刘汝逾等[14]在单自由度线性双侧刚性碰撞模型中引入分数阶微分，分析了该系统在简谐激励下的稳定性和分岔行为。隋鹏等[15]提出了一种含有惯容和接地刚度的新型动力吸振器模型，并详细研究了该模型的最优设计参数。Wang 等[16]提出了一种含有负刚度弹簧元件的三要素型动力吸振器模型，通过最小化幅频曲线的最大值得到了系统最优阻尼比的设计公式。Litewka 等[17]分析了Zener 黏弹性材料所制成Von Kármán 几何非线性板在简谐激励作用下的振动响应，采用谐波平衡法求解了系统振幅响应，分析了参数对阻尼水平的影响规律。

考虑到实际系统中的扰动源往往是两个甚至多个窄带频谱激励源的叠加[18-21]，本文以四元件橡胶模型为研究对象，分析了橡胶等黏弹隔振系统在单频、多频激励下的最优阻尼系数。首先建立了系统无量纲运动微分方程，采用谐波平衡法求解了系统幅频响应并与数值结果相比较，随后得到系统不同参数条件下的幅频响应与力传递率，并计算了系统单频、多频激励下的最优阻尼系数，最后分析了参数对系统幅频特性与振动传递特性的影响规律。

1 系统的力学模型和运动微分方程

图1为四元件橡胶隔振系统的力学模型，该模型由标准线性固体模型（又称Zener 模型）与刚度为K0的弹簧并联而成。质量块 M 在简谐激励F sin(ΩT)作用下往复运动，X、Y 分别表示质量块与无质量节点在竖直方向的位移。

图1四元件橡胶隔振系统

图1 所示系统的运动微分方程为

考虑到橡胶材料的振幅相关性，引入如下无量纲参数：

式中：Fsolidary为系统外激励幅值 F的对照参数，该参数的引入可较为直观地体现橡胶隔振系统的幅值相关性。

进而可得系统的无量纲微分方程为：

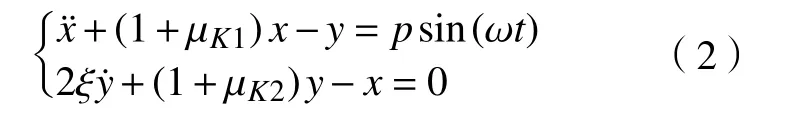
2 系统的幅频响应

下面采用谐波平衡法求解四元件橡胶隔振系统的幅频响应。设图1所示系统的主振动为：

将式（3）代入式（2），略去其中的高阶项，并使等式两边对应谐波项的系数相等，可得四元件橡胶隔振系统质量块与节点的幅值和相角为：

式中：D0=1+µK1-ω2；D1=2ξω；D2=µK1-ω2；D3=1+µK2。

由式（4）可得四元件橡胶隔振系统的幅频响应，并结合数值方法进行正确性验证，为后续基于系统幅频响应计算最优阻尼系数提供必要前提。图2为参数µK1=1．5,µK2=0．05,ξ=0．1,p=2时，谐波平衡法与数值法所得质量块幅频响应对比图，可见两种方法所得幅频响应匹配良好。

图2 质量块幅频响应对比图

3 系统的最优阻尼系数

3.1 系统单频激励下的最优阻尼系数

由式（4）可得质量块振幅放大因子为

图3 不同参数条件下阻尼系数对质量块幅频响应的影响

由图3可知，对于既定刚度比，任意阻尼系数下的幅频响应曲线均交于公共点C =()，因此，总可以找到一条幅频响应曲线，使其峰值点恰好为公共点C，此时的阻尼系数即四元件模型在当前参数域内的最优阻尼系数 ξopt。随着阻尼系数 ξ的增大，系统共振频率逐渐向高频区移动，且当阻尼系数ξ<ξopt时，随着阻尼系数 ξ的增大，质量块最大振幅放大因子βmax逐 渐降低，而当ξ>ξopt后，阻尼系数ξ的增大又会使 βmax逐 渐增大，而ξ 较大时， µK1的增大会使质量块共振峰高于弱阻尼时的共振峰。

既定刚度比下四元件模型的最优阻尼系数ξopt求解步骤如下：

1）明确隔振系统的主要工作频率，选择恰当的刚度比搭配，使系统工作频率远离系统当前参数下的主共振峰；

4）同理选定该刚度比下的另一阻尼系数，计算出公共点所对应的激励频率正实根，所得公共解即为系统最优阻尼系数 ξopt下 的激励频率 ω。

在已选定的刚度比下，使振幅放大因子β(ω,µK1,µK2,ξ)对 激励频率 ω求偏导可得：

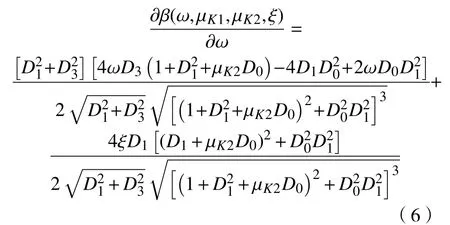
根据上述步骤，选择系统刚度比 µK1=1, µK2=0．01， 可得阻尼系数 ξ从0.05逐渐增大至1时，质量块的幅频响应曲线簇与最优阻尼系数 ξopt下的最佳幅频响应，如图4所示。

µK1=1,µK2=0．01 β(ω,ξ)图7 时 在 参数平面的分布

µK1=1,µK2=0．01图4 时质量块的最佳幅频响应

图4中，绿色曲线 L为各阻尼系数下质量块共振峰随激励频率 ω的变化规律。由图4可知，当前参数下系统公共点C =(1．226,2．020)。黑色曲线S 是以公共点为共振峰值点的最佳幅频响应曲线。通过前面的计算可得系统当前参数下的最优阻尼系数ξopt=0．41。

由图5可知，取刚度比µK1=3,µK2=0．01，可得阻尼系数ξ 从0.05逐渐增大至1时，质量块的幅频响应曲线簇与最优阻尼系数ξopt下的最佳幅频响应。此时系统公共点C =(1．872,2．012)、最优阻尼系数ξopt=0．27。

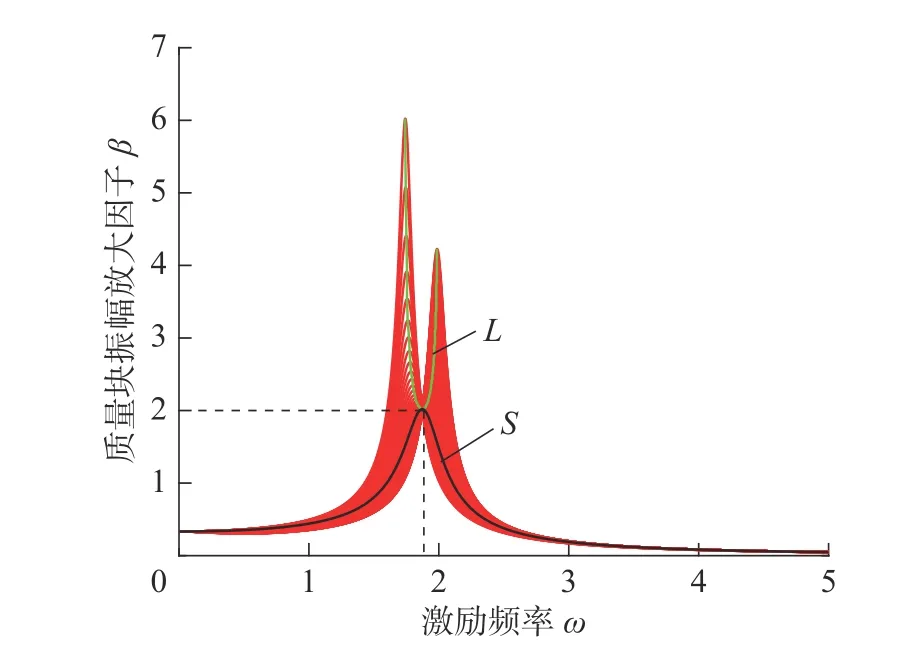
µK1=3,µK2=0．01图5 时质量块的最佳幅频响应

3.2 系统多频激励下的最优阻尼系数

由于实际工作环境中机械系统所受激励通常为多频率激励，下面分析计算四元件橡胶隔振系统在多频激励下的最优阻尼系数。假设系统受多频谐激励的形式为，通过无量纲量pi=Fi/Fs将激励无量纲化，依据外激励形式设出系统响应，基于叠加法及谐波平衡法求得系统响应，最后采用均方根处理所得响应，可得系统多频激励下质量块的振幅放大因子

以 i=2为例，此时系统受双频激励作用，该激励无量纲化为 p1sin(ω1t)+p2sin(ω2t)，其中 p1=F1/Fs，p2=F2/Fs。取系统参数µK1=1,µK2=0．05,p1=1,p2=1， 假设ω2=3ω1， 基于式（8）可得阻尼系数ξ从0.05逐渐增大至1时，系统双频率激励下的质量块的幅频响应曲线簇与最佳幅频响应，如图6所示。

图6 双频率激励下质量块最佳幅频响应

由图6可知，系统在双频激励下的幅频响应曲线有两个共振峰，系统幅频响应曲线也有两个公共点，且这两个共振峰（或公共点）对应频率和 ω1与 ω2的比值相同。采用四元件模型单频激励下最优阻尼系数ξopt同理的求解步骤可求得系统特定参数下的最优阻尼系数 ξopt=0.42，使得系统幅频曲线两个共振峰均为最低状态。本文最优阻尼系数计算方法在双频激励下的无差别应用，证明了该方法在多频激励下的四元件橡胶隔振系统最优阻尼系数计算的普适性。

4 系统的隔振性能分析

4.1 两维参数下系统振幅放大因子的分布规律

为更加全面地反映四元件橡胶隔振系统的隔振性能，下面分析系统振幅放大因子 β在两维参数域(ω,ξ) 和(ω,µK1)内的分布规律，如图7和图8所示，因刚度比µK2对系统隔振性能的影响规律与 µK1相似，此处不再赘述。结合振幅放大因子的定义可知，系统在振幅放大因子 β<1的区域内具有减振效果。由图7和图8可知，改变系统阻尼系数与刚度比可达到调整系统减振效果的目的，通过ξ 调整阻尼系数也 可实现系统共振频率的小范围微调。

ξ=0．2,µK2=0．01 β (ω,µK1)图8 时 在 参数平面的分布

由图7可知，随着阻尼系数 ξ的增大，系统共振峰先减后增，并在阻尼系数ξ 取ξopt=0．41时取得最小主共振峰；而当 ξ增大时，系统共振峰对应的频域宽度有所减小，低频范围内的隔振频宽逐渐增加。由图8可知，随着刚度比 µK1的增大，系统共振峰逐渐降低、低频范围内的隔振频宽逐渐增加，说明刚度比 µK1增大可明显改善系统的隔振效果。实际应用中通过调整刚度比 µK1与 µK2可使系统共振区远离机械系统工作主频，进而使系统呈现出最佳的隔振效果。

4.2 系统参数对力传递率的影响

力传递率作为评价系统隔振性能的指标，定义为隔振系统受到激励力的作用后传递到地基的力幅值与激励力幅值的比值[22-24]，能更深入地揭示系统的振动传递行为。以单频激励时的系统为研究对象，分析参数对系统力传递率的影响规律。记录系统所受无量纲外激Fexcitation= p sin(ωt)，记录通过四元件橡胶隔振系统传递到基座上的力为Ftransmissibility，结合式（2）可得系统力传递率

其中

式中： x、y、y˙分别为质量块位移、节点位移与节点速度。

将式（4）代入式（8）和式（9），可得系统广义力传递率

选择系统基准参数p=3,µK1=0．3,µK2=0．03，由式（11）可得刚度比 µK1、 µK2及阻尼系数ξ 对四元件橡胶隔振系统力传递率的影响规律，如图9所示。

图9 参数对系统力传递率的影响

由图9可知，增大刚度比 µK1与 µK2都会使系统力传递率显著增大、共振峰向高频方向偏移。但刚度比一定时，增大阻尼系数会使系统力传递率峰值先减小后增大，并且不同阻尼系数下的力传递率曲线也形成了一个公共点，因此可以参考前文方法计算出系统当前参数下的最优阻尼系数，使系统力传递率曲线的共振峰值恰好为公共点。图10为参数µK1=1, µK2=0．01时系统的最佳力传递率，此时系统公共点C =(1．226,1．401 9)，最优阻尼系数 ξopt=0.41。

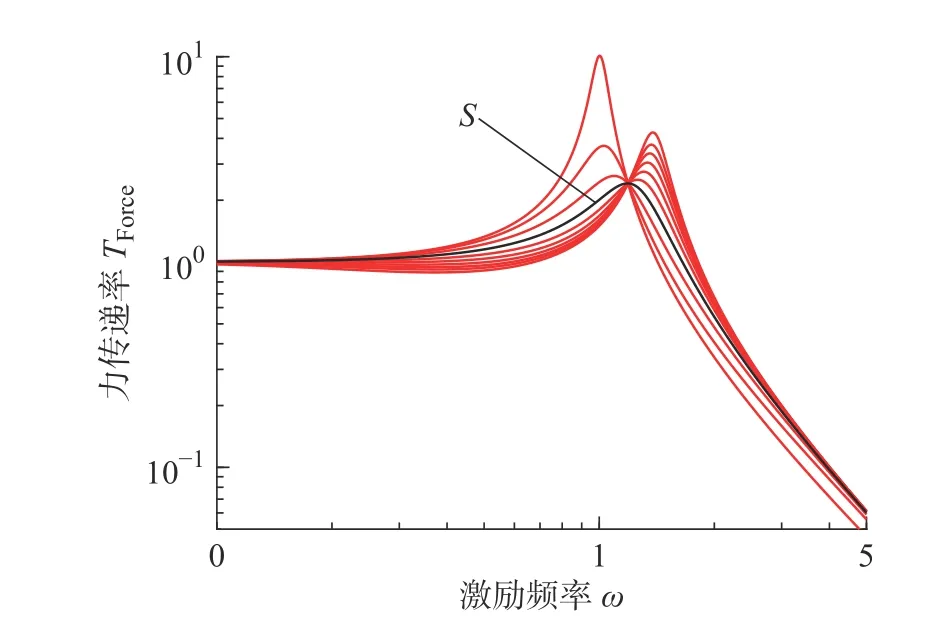
=1, µk2=0．01图10时系统的最佳力传递率

5 结论

建立了四元件橡胶隔振系统的动力学模型，求解了系统在单频激励与多频激励下的振动响应，得到了系统幅频响应曲线与力传递率曲线，推导了系统最优阻尼系数的计算方法，并分析了系统参数对隔振性能的影响，得出以下结论：

1）四元件橡胶隔振系统共振峰不仅受刚度比影响，还与阻尼系数的选取有关。增大刚度比 µK1或µK2可使系统共振峰向高频方向转移，反之则向低频偏移。基于这一特点可设计出恰当的刚度比搭配，使系统共振峰远离被隔振系统工作主频，从而呈现出最佳的隔振效果。在不降低系统静挠度的条件下，还可通过调整阻尼系数ξ 实现系统共振频率的小范围微调。

2）既定刚度比时，系统不同阻尼系数下的幅频响应曲线与力传递率曲线均通过一个公共点，则可基于此计算出一个最优阻尼系数 ξopt，使其对应幅频响应曲线或力传递率曲线的峰值点恰好为公共点，此时系统幅频响应曲线或力传递率曲线共振峰为当前参数下最低状态。上述方法同样适用于多频率激励系统最优阻尼系数的计算。

3）随着刚度比 µK1、 µK2或阻尼系数 ξ的增加，系统共振峰对应的频域宽度有所减小，低频范围内的隔振频宽逐渐增加。

上述研究结果与方法，可为橡胶等黏弹隔振系统的参数设计与优化提供一定的理论依据。