F=1旋量玻色-爱因斯坦凝聚的向列压缩
2022-12-02杨超楠郑任菲赵兴东周鲁
杨超楠,郑任菲,赵兴东,周鲁
(1.华东师范大学 物理与电子科学学院,上海 200241;2.合肥工业大学 物理学院,合肥 230009;3.河南师范大学 物理学院,河南 新乡 453007)
与标量玻色-爱因斯坦凝聚[1-5](Bose-Einstein condensate,BEC)相比,旋量BEC是磁性超流,所以展现出更加丰富的物理性质,成为近几年来实验和理论的研究热点[6-13].很多有趣的物理学现象在该体系中被观测到,比如量子纠缠[7]、自旋压缩[8]和自发退磁现象[14]等.因而,旋量BEC领域的研究具有极大的价值.自旋压缩对量子信息的研究有重要的意义.在超高精密测量领域的作用也尤其突出.与自旋压缩不同,向列压缩引入了高阶的向列张量,展现了更加丰富多元的压缩性质[15].CHAPMAN等人[16]首次在实验上实现了旋量BEC的向列压缩.2013年,他们又发现了不稳定点与压缩之间的关系[17].同年,日本东京的一个小组将向列压缩归类为第二类压缩,并且给出了详细的分类依据[18].很快,利用周期性微波脉冲将自旋向列压缩存储在旋量BEC中的方案出现.在适当的脉冲周期和相移条件下,压缩可以增强并保持较长时间,从而实现最大压缩的存储[19].同时,腔场中的BEC也可以产生向列压缩[20].
本文从旋量BEC的模型[21-23]出发,在理论上总结了自旋向列压缩的产生和动力学演化行为[24],在自旋向列球上展示了极化态为初态的自旋向列压缩的物理特性和压缩图像.然而,仅仅描绘极化态的压缩行为显然是不充分的,缺乏普遍性,因此,还研究了在任意初始态下系统的向列压缩行为.
1 旋量BEC模型的介绍
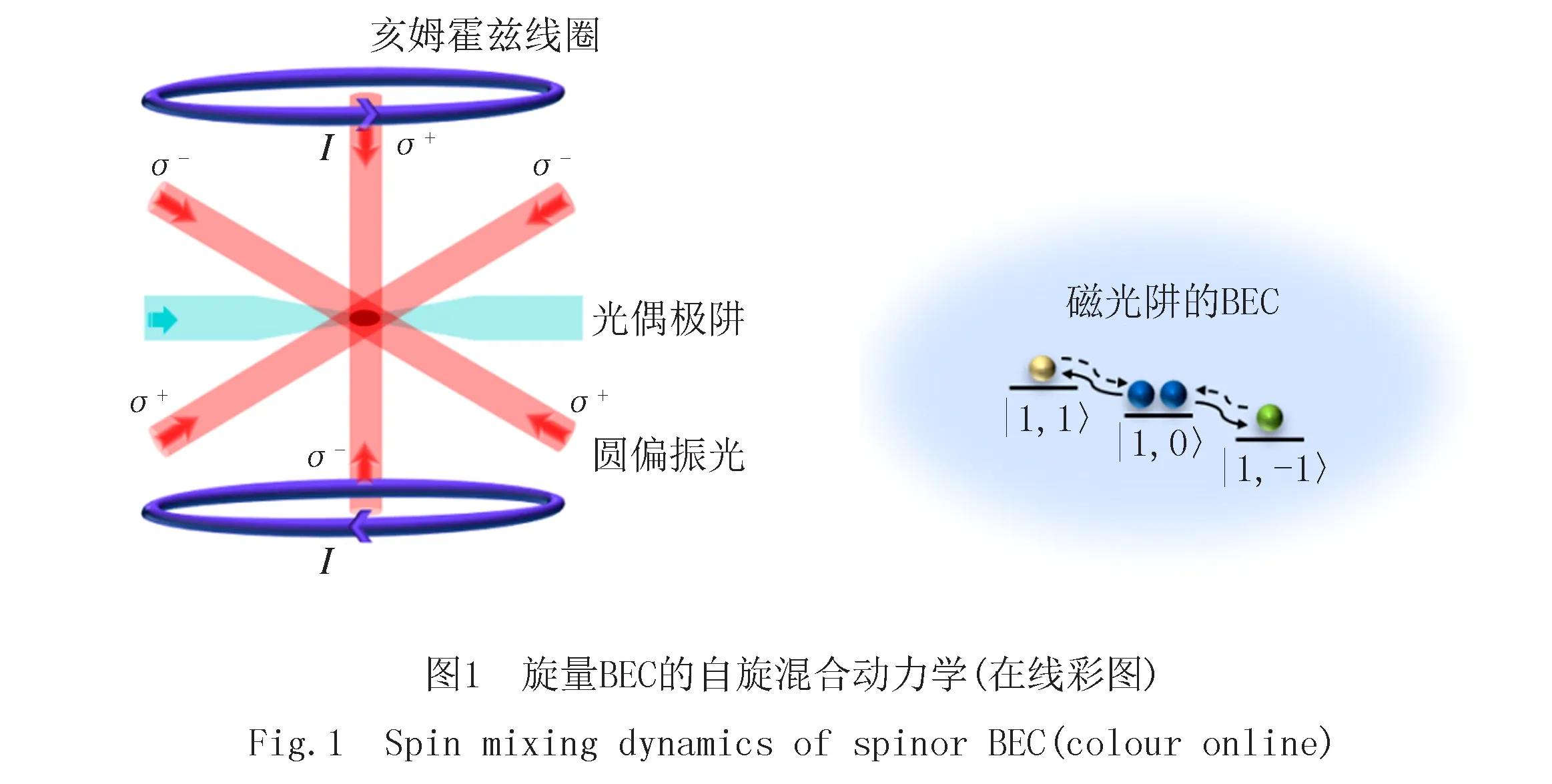
考虑被冷却并囚禁于三维磁光阱中的超冷原子,用于产生旋量BEC.对于F=1的旋量BEC,自旋磁量子数mF是-1,0,1,对应的3种塞曼态|F,mF〉:|1,1〉,|1,0〉|1,-1〉,如图1所示[25-26].根据单模近似原理,在有限的磁场中旋量BEC的哈密顿量[27-28]
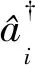
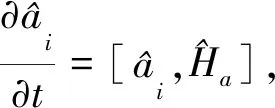
(1)
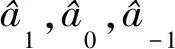
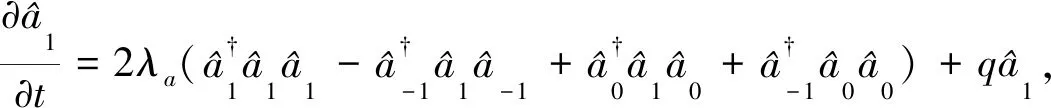
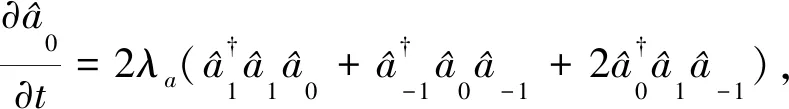
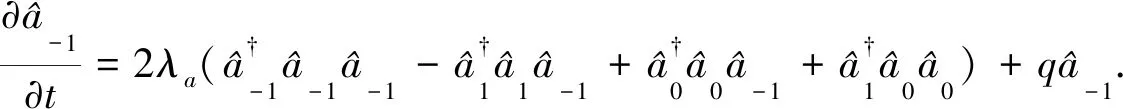
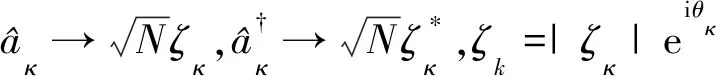
(2)
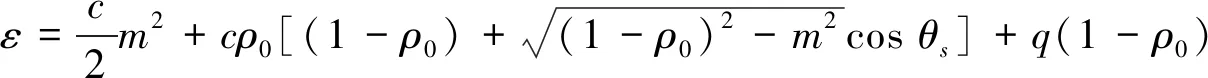
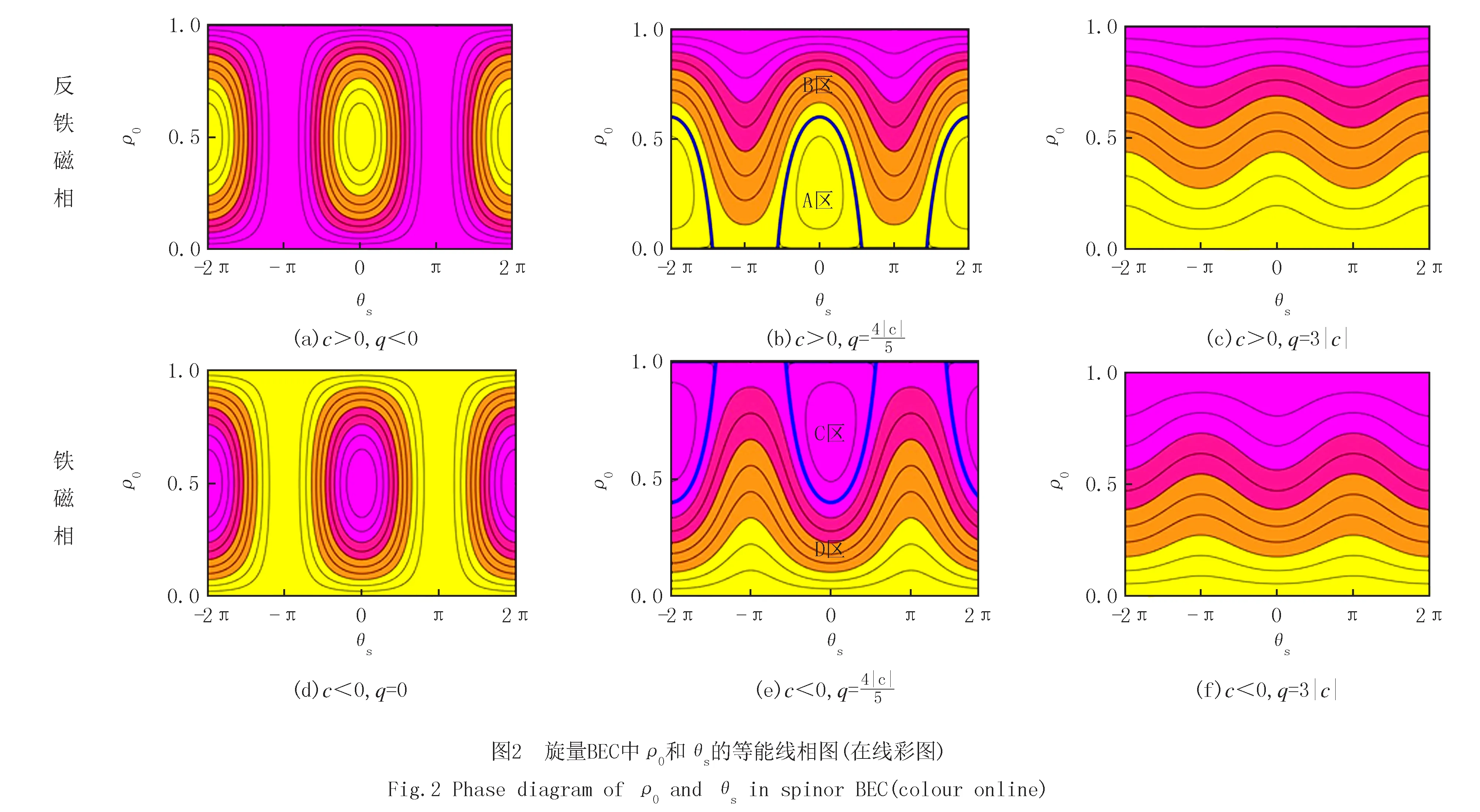
当2个区域都存在的时候,就会有分离线的存在.c<0,q>0时,分离线对应ε=0的等能线,ρ0=1对应系统的不稳定点;c>0,q>0时,分离线对应ε=q的等能线,ρ0=0对应系统的不稳定点.等能线的相图可以用于预测初态未来的演化趋势[23].
然而,平均场方法是在粒子数趋向于无穷大并忽略量子起伏的情况下得到的.显然,在粒子数有限的情况下,与量子相关的性质,如压缩、涨落等无法通过平均场方法体现.虽然全量子方法可以很好地描述量子性质,但是其计算效率较低.当原子数目比较多时,全量子方法可能会达到计算机极限.而半经典的截断维格纳近似方法[30]结合了平均场方法的思路和全量子中的涨落特点,用一个维格纳分布代替一个点来描述初态.这在解决压缩这类问题中展现出巨大的优势.既能保证计算速度,又可以准确地描述系统的量子特性[31-32].
2 向列压缩
在研究自旋压缩的时候,通常会定义自旋算符

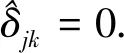
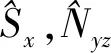
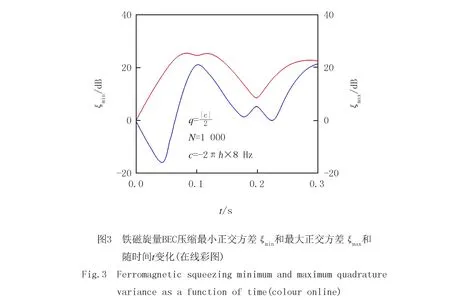
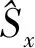
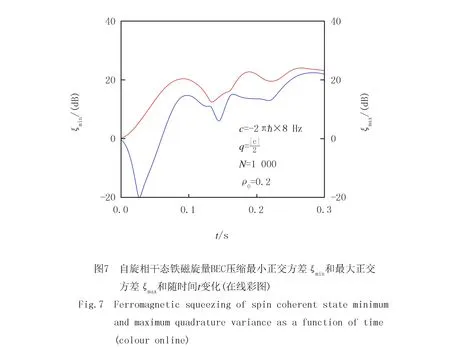
应用变换ξ→10lgξ,相应地,ξmin≥0 dB代表没有压缩;ξmin<0 dB代表发生了压缩,且ξmin的值越小,代表压缩越明显.可以看出,初始的时候ξmin=0 dB,代表没有压缩,随着时间演化,最小正交方差不断变小,直至t=43 ms,最小正交方差达到最小值,随后压缩仍然持续一段时间,但是压缩强度逐渐变小.
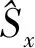
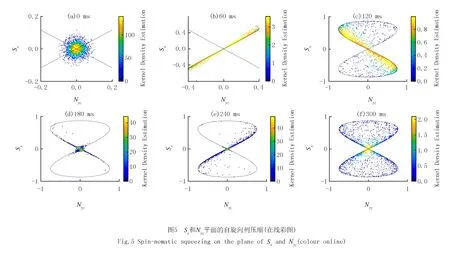
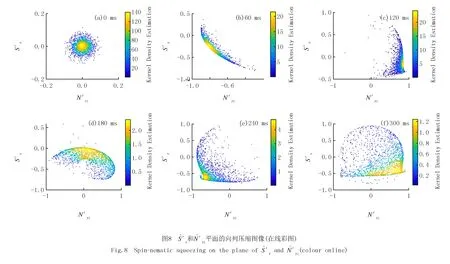
如图4(a),初始时刻态是一个在球体北极的圆形分布.图中白色的线是等能线,其中穿过上顶点(不稳定点)(0,0,1)的等能线对应相图的分离线.将初态制备在不稳定点,随着时间变化态会沿着分离线压缩,成为一条细长的曲线.然后散点会沿着分离线散开(图4(c)).在180 ms时,散点开始沿着分界线的另一支压缩,在北极处形成交叉的图像.随着压缩的减弱,散点最终散开,但是并非完全散开,而是集中在分离线所在的曲面上(图4(f)).将图4中的一系列图像进行投影,使用颜色标记散点的密度,得到图5.
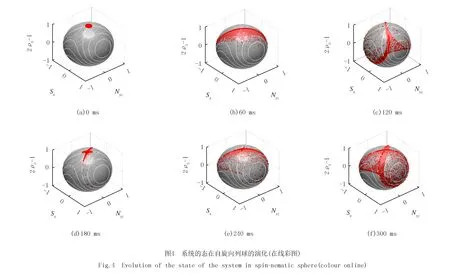
在图5中,黄色代表散点的密度较大,其次是绿色和蓝色.从投影图可以更加直接观测到Sx和Nyz.初始时刻,Sx和Nyz的分布近似是一个圆,说明此时没有发生压缩.随着时间的演化,在60 ms时,Sx和Nyz的分布集中在一条线上,且这条线是与分离线重合的,说明此时沿着分离线发生了压缩,并且压缩越强,散点构成的区域面积越小,几乎完全分布在分离线上;相反,压缩越弱,散点逐渐分散(图5(c)).Sx的涨落小于Nyz的涨落,说明对Sx有更加准确的测量.在180 ms时,在图5(d)中散点开始沿着分离线的另一支压缩.图5(f)和图5(c)的形状相似,但是颜色分布有较大的差别,图5(c)中黄色区域集中在中心和分离线上,而图5(f)中黄色区域较少且只集中在中心,蓝色区域散布在分离线围成的闭合图形中,此时压缩强度较弱.由此可见,制备在不稳点的初态总是沿着分离线压缩的.
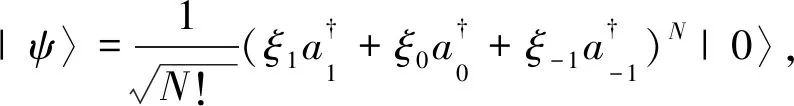
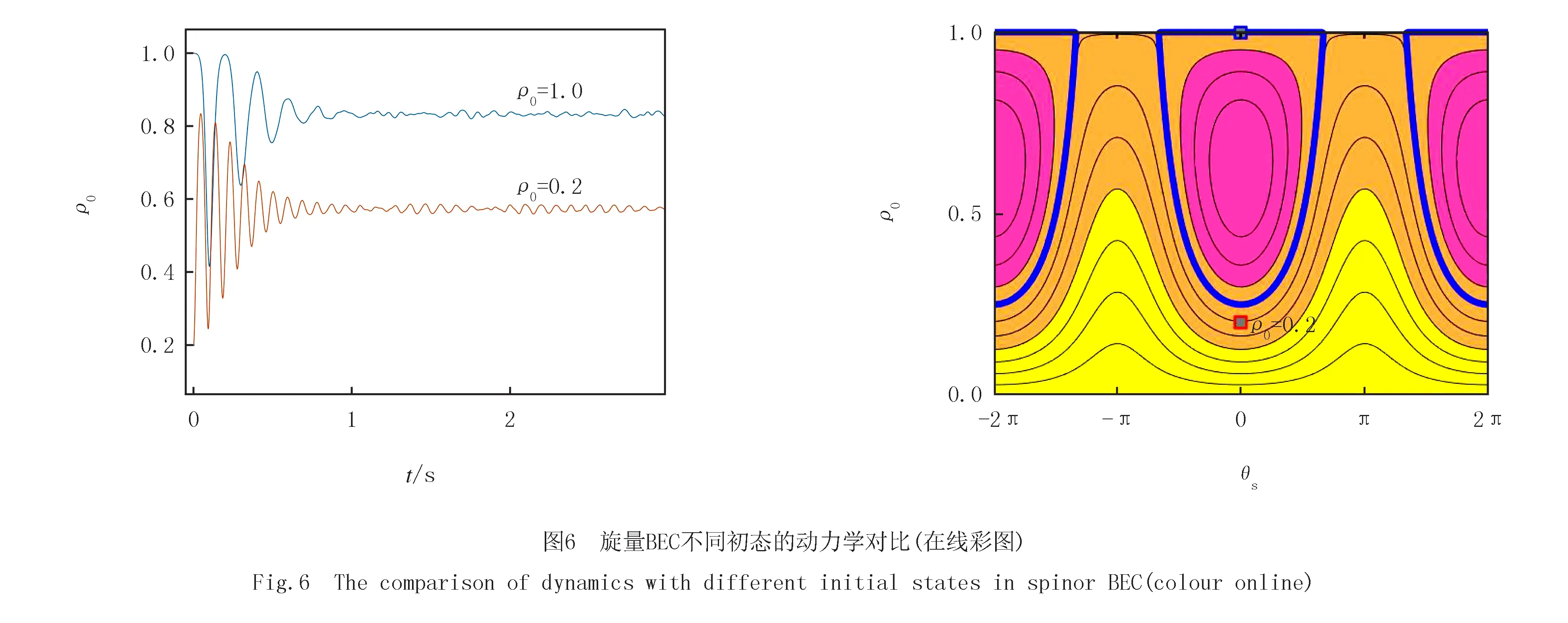
在旋量BEC的铁磁相(c<0,q>0)中,不稳定点往往对应ρ0=1的极化态,图6(a)中给出了初态为ρ0=0.2的自旋相干态和初态为ρ0=1的极化态随时间演化的动力学图像,可以看到两种初态最终都趋向于稳态,趋于稳态的时间略有不同,图6(b)则标出了不同的初态在相图的位置.
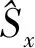
3 总 结
本文从理论上回顾了旋量BEC系统中的自旋向列压缩特性,推导出了向列压缩参数的形式,并从数值上模拟了在不稳定点对应的态随时间演化的规律.通过模拟自旋向列球及其投影图更清楚地展示了旋量BEC系统中丰富的向列压缩特性.并且,还研究了任意初态情况下系统的压缩性质,发现某些自旋相干态的压缩效果比极化态更佳.
