基于循环神经网络模型的延河流域径流预报研究

高延香

(陕西省延安市宝塔区水资源与节约用水中心，陕西 延安 716000)

0 引 言

尽管水对于所有形式的生活都是必不可少的，但有时也会具有破坏性。洪水，山体滑坡和泥石流都是由多余的水引起的[1]。世界上许多地区都容易遭受与水有关的灾害，其破坏以及由此造成的人员伤亡正在增加。在各种与水相关的灾害中，洪水灾害在造成的人员伤亡和破坏程度方面更加严重。还必须指出的是，不仅因为人口迁移到经济前景更好的地区，灾难的数量在增加，而且受影响的人数也在增加。延河属于典型的多泥沙河流，是黄河中游泥沙主要输入区之一，也是区域内延河流域地质洪涝灾害高发的原因之一。因此，预报延河流域的径流量是十分重要的。

缓解洪灾可以通过预报径流量来提前预测洪水，以便早作准备、减少灾害损失。但河流流量时间序列非常复杂，并且包含各种频率分量[2]。如果利用传统物理性的水文模型来预测径流量，虽然可以解释径流变化规律，但需要输入许多参数，太过复杂[1,3]。而在水文建模中，发现神经网络是一种合适的工具。如果对系统的水文地质特征了解不足，并且相比于理解物理过程，认为预测的准确性更为重要的情况下，那么黑箱型模型是可行的选择。循环神经网络(RNN)属于黑箱型模型[4]，可用于捕获复杂系统的非线性行为。循环神经网络模型已经用于降雨-径流过程中，并且不断被改进[5]，且RNN在时间序列的预测方面具有一定的可行性。

因此，本文将利用循环神经网络来预测延河流域的径流量，以期所建模型可以有效预报该流域的径流量，提早预防，减少灾害的发生。

1 材料方法

1.1 数据预处理

在训练RNN模型之前，利用归一化公式对数据进行处理，此类处理有益于模型的训练[3]。处理后的数据大小范围在[0，1]内。公式如下：

(1)

式中：xnorm、xi、xmin和xmax分别为数据的标准化值、观测值、最小值和最大值。

1.2 RNN模型

循环神经网络(RNN)常用于时间序列预测任务[4,6]。RNN被认为是递归的，因为它们对序列中的每个元素执行相同的任务，并且当前输出取决于先前的计算。在RNN中，单元之间的连接形成有向循环。RNN的结构见图1。

图1 RNN网络结构图

该算法迭代按以下方程式进行：

ht=tanh(Uxt+Wht-1+b)

(2)

xt=tanh(Vht+c)

(3)

其中：ht为根据先前的隐藏状态ht-1计算出的隐藏状态；xt为当前时间的输入值；U、W和V分别为在RNN中训练的输入层到隐藏层的参数，隐藏层到隐藏层的参数和隐藏层到输出层的参数。

RNN模型的参数按经验设定如下，主要有：隐含层神经元数目32，迭代训练次数为250次，核函数采用Adam函数，误差函数用均方误差来评价模型精度，设置误差标准为0.001。本研究利用Matlab R2018进行模型训练与测试。

1.3 模型评价指标

通过均方根误差RMSE来评价模型的效果。RMSE越接近于0，意味着模型精度越高，预测效果越强。RMSE的计算公式如下：

(4)

2 实例分析

2.1 研究区站点概况

安塞县延河干流设有安塞水文站[7]。安塞水文站设立于1973年6月，位于安塞县真武洞镇，地理坐标E109°19′，N36°56′，控制流域面积1 334 km2。安塞水文站有1981年～至今实测水文资料。本研究选用1981-2004年的逐月径流数据用以模型的训练，用2005-5015年的逐月径流数据用以模型的测试。

2.2 模型预测效果

图2为模型训练过程中，训练集和测试集的均方根误差随着迭代次数的变化。由图2中可以看出，训练集随着迭代次数的变化，均方根误差先快速骤降，然后再缓慢下降。当迭代次数达到175时达到最低点，随后基本保持不变。测试集也有类似的规律，均方根误差先骤降，但其在骤降到最低点后，又有缓慢的回升现象。不过与训练集相比，其均方根误差更低。因此，本文选用迭代次数为175次的模型作为径流预测模型。

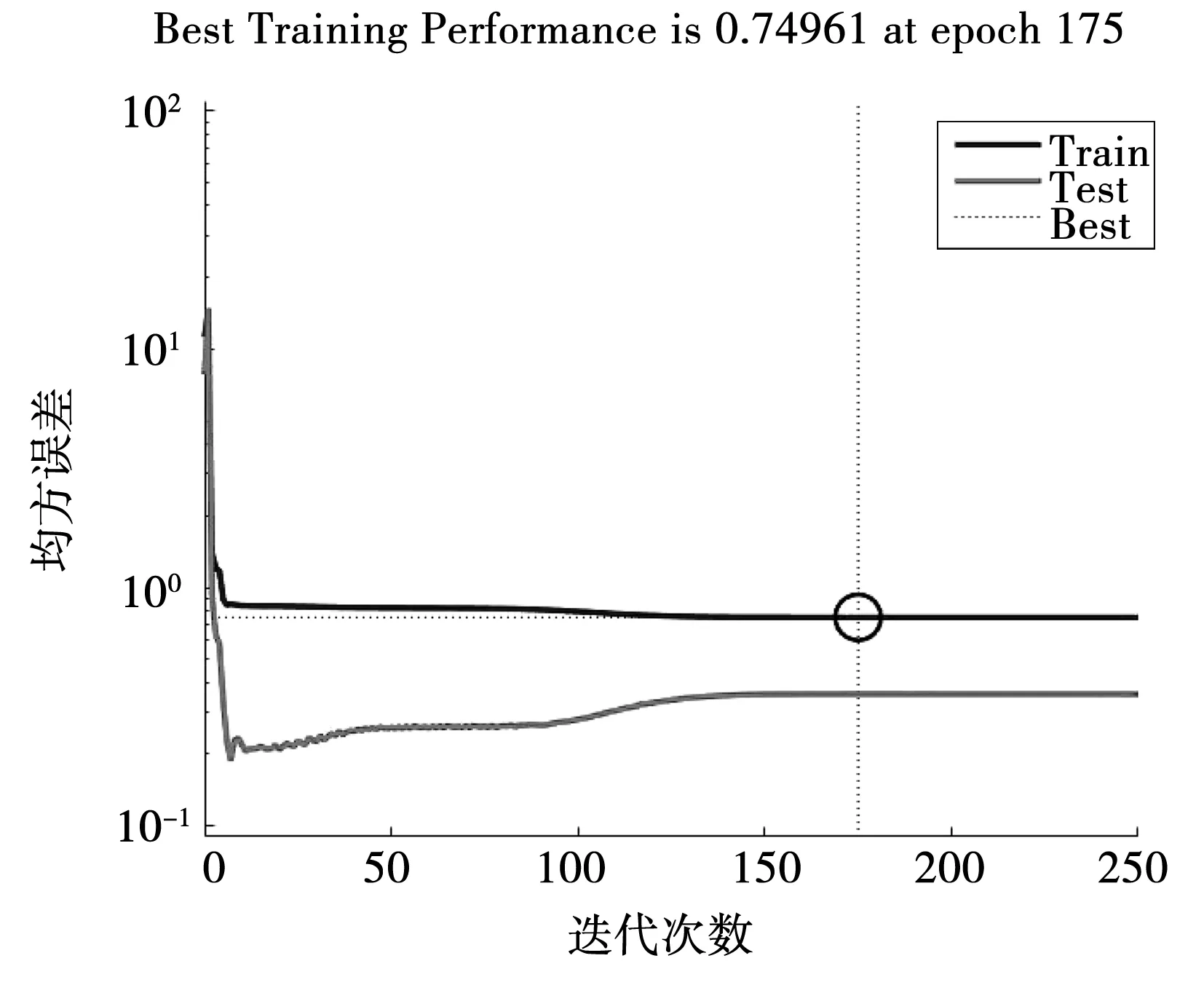
图2 RNN模型最佳训练结果

为了进一步评价所建的径流预测模型的效果，本文绘制了图3、图4。图3为2005-2015年的逐月径流预测值与实测的变化图，从图3中可以发现，实测曲线与预测曲线的特征基本一致，但是在部分细节部分两者之间具有明显的差异，说明模型在预测时，仍有一些偏差。

图3 安塞站2005-2015年逐月径流量预测

图4 安塞站2005-2015年逐月径流量偏差分布结果

图4为实测值与预测值之间的偏差柱状图，由图4可知，2005与2013这两年，模型在预测时具有明显高于其余年份的偏差，但其径流的大致情况仍可以得到体现，其模型预测的RMSE仅380 m3/s。对误差进行统计分析，见图5。

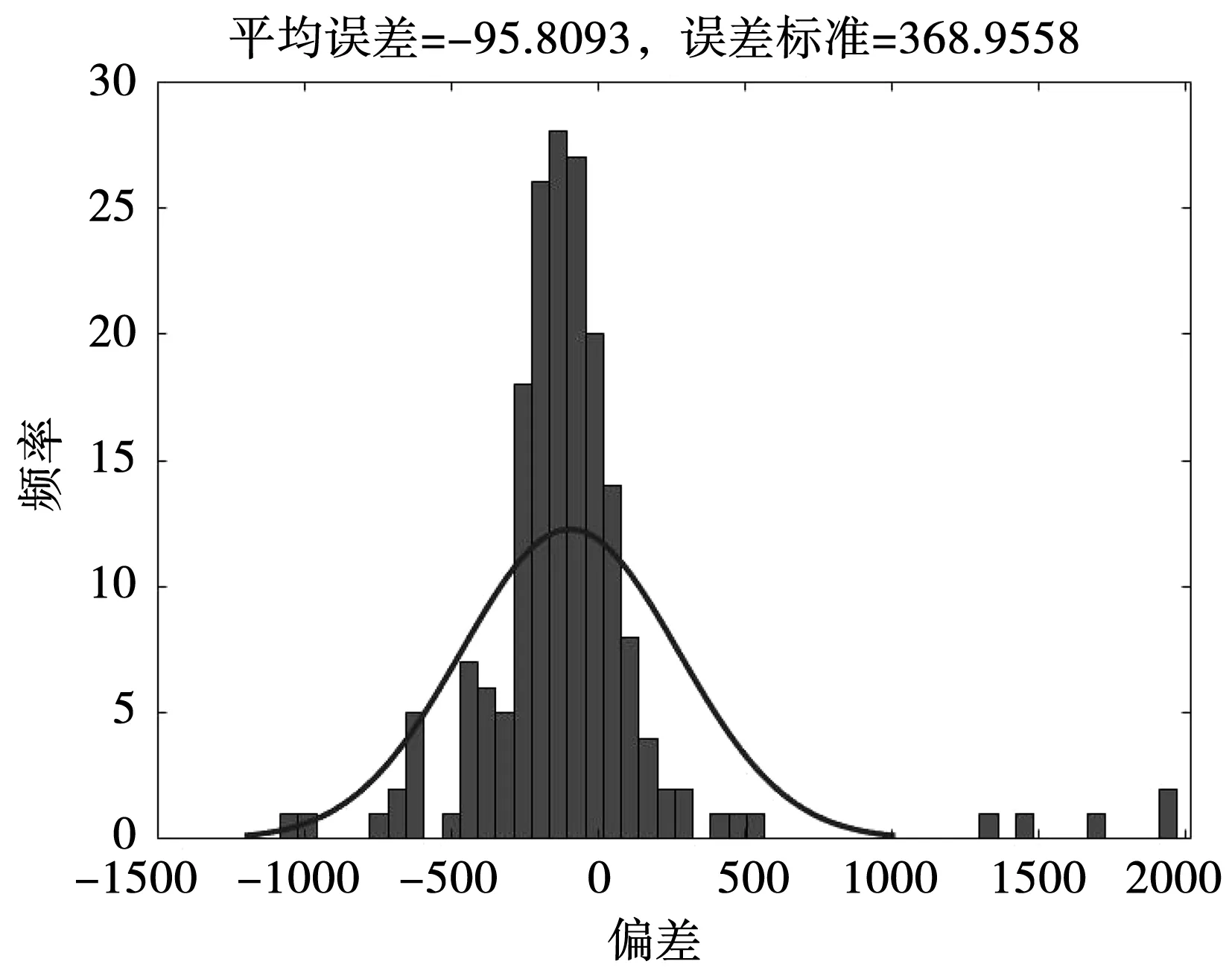
图5 安塞站2005-2015年逐月径流量偏差统计结果

图5中的分布说明，预测误差大部分集中在零附近，所以本文所建的安塞站逐月径流预测模型是具有一定预测能力。

本文还对模型效果进行了相关性分析。图6为实测值与预测值的散点图，R为相关系数。整体的相关系数可达0.62，建模集的相关系数为0.61，而测试集的相关系数可以高达0.77。由图6中的拟合线与1∶1直线的夹角可以发现，模型对测试集的效果比较好。总的来说，本文利用RNN来预测安塞站的逐月径流量是有效的，虽然在某些年份有相对较大的误差，但是预测值仍然与实测值较为接近。

图6 安塞站逐月径流量实测与预测散点图

3 结 论

本文将RNN模型应用于延河流域的逐月径流预测，结论如下：

在安塞站，RNN模型具有一定的适用性，其迭代达175次时，具有最佳的效果。而且，用以预测2005-2015年逐月径流量，有较好的效果，均方根误差为180m3/s，实测值与预测值的相关系数可达0.77。模型的建立可为该地区的径流预测及灾害预报提供一定的参考。