引水隧洞岩体节理塑性区特征规律研究

2022-12-02梁家盛

水利科技与经济 2022年11期

梁家盛

(深圳市水务规划设计院股份有限公司，广东深圳 518000)

1 概述

随着科技的发展，我国对基础建设工程也更加全面。其中，引水隧洞工程给一些贫瘠地区带来便利和机遇，越来越受到国家的重视。许多水电工程在开挖过程中，都会形成空洞现象，使其岩体的塑性区发生变化，进而扩散，从而影响整体的稳定性。因此，对塑性区的特征规律进行研究具有重要意义。

袁平[1]提出地层引水隧洞的施工支护关键技术，并结合实际应用和数值模拟技术，证明了该技术的可行性。周泽林[2]根据实际工程应用，对引水隧洞支护体系软弱岩体受力特征进行研究，分析支护效应情况，测出软弱岩体的发展和扩张趋势，分析支护结构的可行性。边义成[3]对隧洞施工中的影响因素进行总结，并对相应的问题提出了解决方案。魏彦军等[4]对开挖隧洞过程中容易出现的问题进行探讨，分析有效提高岩体抗劈裂性能和防渗性能的解决方法。钟权等[5]研究典型开挖断面，通过利用有限元软件，研究断面在开挖过程中的损失特性。黄晓锋等[6]对引水隧洞的外界条件影响进行研究，通过有限元数值模拟分析应力场、结构面在不同分布情况下，引水隧洞特性机理。付代光等[7]通过分析引水隧洞岩石体完整性，通过实践综合证明测井技术对岩体勘察的优越效果。钟权等[8]以引水隧洞钻爆模式开挖形式为研究对象，通过有限元分析模拟了该过程，分析钻爆模式开挖形式的程序、循环进尺和药量对岩体的损害程度。吴文平等[9]分析水电站引水隧洞的基本条件，通过数值分析和支护设计并结合施工过程，建立岩体的破坏方法，分析该方法的通用性和实际意义。刘宁等[10]通过研究岩体由于强度和应力引起的损伤，通过有限元数值模拟对关键点处于应力状态进行分析，揭示损伤特征以及分布特征。

上述文献主要针对引水隧洞岩体的损失情况进行分析，但未对节理塑性区特征规律进行研究，也未对隧洞形状进行模拟研究。本文以某项目引水隧洞为主要研究对象，基于摩尔-库仑准则，推导出计算公式并对参数的推理、塑性区范围的预测及原因进行分析，为我国引水隧洞节理裂隙塑性区的变化规律提供理论基础。

2 塑性区理论

2.1 工程概况

某项目引水隧洞所在地区为多地震带，且地势较高。引水隧洞需通过18 km的山区地带，地带沿线山势险峻，穿越多片山区，且山体多为裸露边坡，河谷狭窄，地势险翘，因此选择岩体较硬且不是破碎状态的地区为主。采用水压裂碎法测量引水隧洞的应力情况，各孔岩体厚度为560 m。相应桩号上设置3个钻孔，分别为K1、K2和K3，3个钻孔的布置情况见表1。

表1 K1、K2和K3布置情况

2.2 判别标准

由屈服准则相关理论可知，微元体荷载作用的应力情况见图1。通过应力莫尔圆可以画出其应力状态，见图2。

图1 应力情况

图2 莫尔圆

抗剪强度一般由应力莫尔圆的状态示意，其主要公式为：

τ=c+σtanφ

(1)

式中：c为黏聚力；φ为内摩擦角。

从图2不难发现，其中有相交、相切、相离，这些表示不同的应力状态。由于微元体达到其抗剪强度时，就会处于破裂状态。因此，应力莫尔圆的相切和相离是较为合理的状态。而对于相交状态，由于微元体会破裂，因此为塑性状态。其具体公式为：

(2)

(3)

式中：c、φ分别为岩体固有的性质。其强度为塑性状态，需通过解析运算或者数值模拟得到主应力值，并通过这些值判断其状态。

对于岩体塑性区域范围预测，可以得出其基本公式。其中，假设引水隧洞的长度为无限长，且其它岩土为理论状态，由此推算出引水隧洞的塑性区范围为：

(4)

式中：p0、R0分别为深部圆形隧洞竖向荷载和圆形隧洞半径。

3 计算模型

3.1 计算参数

采用三维离散元软件，通过数值模拟建立引水隧洞三维模型。以某地的应力测试结果以及对其地质的勘察情况，建立40 m×40 m×40 m的三维模型，设置其基本形状，截面节理分布模型见图3。

图3 引水隧道截面节理分布模型

图3中，引水隧洞宽4.6 m，高5.3 m，在模型4个侧向边界增加水平固定位移约束，在其下边界有固定的位移约束，在垂直方向施加11 MPa的应力强度。采用M-C屈服准则为主，建立模型。引水隧洞分布10个观察点，每个观察点间距为4 m。模型建立后，与Kastner计算方程(后面简称计算方程)和式(4)计算结果进行验证，若三者结果相近，则可证明理论公式的准确性。力学参数见表2，节理面参数见表3，节理组参数见表4。

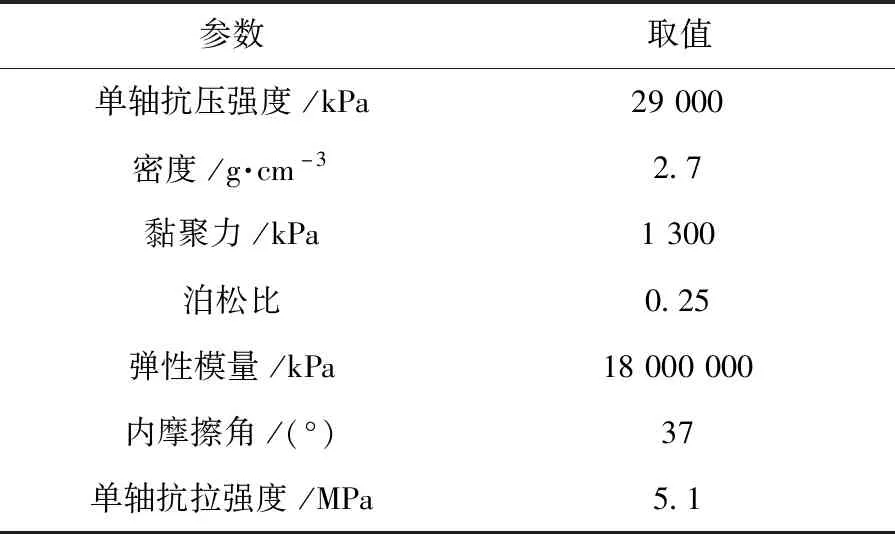
表2 力学参数

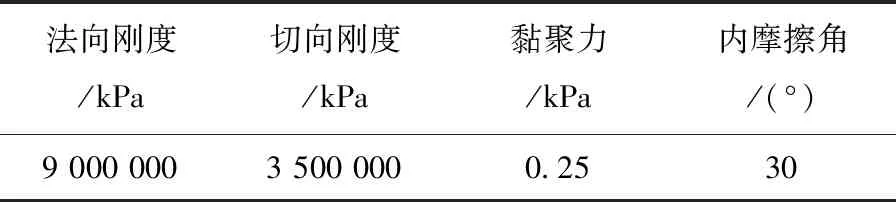
表3 节理面参数

表4 节理组参数

3.2 范围预测

由3.1一节得出的数据可以发现模型的初始应力。其中，塑性区范围和半径对比见图4、图5。对于塑性区范围，以其中的上部圆形区域为研究对象。

通过图4和图5可以发现，当p0=5 000 kPa时，其周围布满均布荷载，深度为0.5 m，但均布荷载在其左右时，底板塑性区深度达到0.98 m。当p0=7 500 kPa时，其值增大40%，深度为0.7 m，且底板塑性区增加至1.1 m。当p0=10 000 kPa时，增加0.8 m。由此可以看出p0，值越大，分布情况越均匀，深度越深。这是因为在模型附近出现应力，使其应力远小于模型的抗拉强度，由此不会产生破坏现象，但却会导致应力分布极不均匀；当应力增大，超过其抗拉强度，则出现破坏。面积参数对比见图6。

图4 塑性区范围

图5 半径对比关系图

图6 面积参数对比关系图

由图6可知，式(4)的计算得出的塑性区面积参数要远弱于其他方式，这说明本文公式计算参数为塑性区面积参数的低数值提供了参考。其中，数值模拟出的塑性区面积参数值的结果最好，一直优于其他参数形式。由图6可知，式(4)的计算结果随初始应力变化，但变化的较为缓慢，在10MPa时，其值与方程计算和数值模拟相差巨大。总体而言，无论是数值模拟还是方程计算或者式(4)计算，其塑性区面积参数都与初始应力呈正相关。

3.3 因素分析

在地应力场中，通过平均水平应力与垂直应力的比值定义为侧压力系数，其对引水隧洞岩体的破坏情况主要是在开挖之后导致的。由截面节理分布图(图3)可知，在该处分布有两组节理在往深处拓展，各方向塑性区范围均增加，尤其当有节理面分布情况在左侧或者底部时，塑性区形状近似矩形。

关于构造节理对岩体塑性区的影响研究，模式与上述一致，参数相同。首先进行开挖模拟，同时进行有节理的模型计算，并与无节理结果进行对比，结果见图7。

图7 有无节理模型大小对比

由图7可知，不同监测点的深度是不一样的。对于监测点1、2、5和10，无论有无节理，其深度都是一致的。其中，监测点5深度最低，深度值为0.5 m。而对于监测点4、6、7、8和9可以发现，有节理的深度要深于无节理情况下的深度，这是因为有节理的底板塑性区范围有较大差异，尤其在交叉节理左边容易与底板处交接。通过图6可知，最深差距达到2.5 m。

对于开挖过程塑性区分布影响，分析岩体在开挖过程中与塑性区发展情况，对10个施工开挖点进行分析，见图8。

图8 开挖累积塑性区范围

由图8可知，4个施工步在开始开挖时，监测点的附近没有岩体发生塑性变化；但施工步在7以及7之后可以发现，深度不会随着监测点的变化而变化。所有监测点的施工步在第6时，其塑性范围的变化趋于稳定，并且不会随着施工步的增加而增加。因此，在施工步为第6时，就可以判定其趋于稳定，且监测点6的范围变化最大，而监测点1的变化范围最小。由此可以分析，对于监测点而言，当其值在最中间时，其变化范围最大。