远距离近地面爆炸空气冲击波计算的网格尺寸优化与验证*

2022-12-02胡志乐马亮亮

爆炸与冲击 2022年11期

胡志乐，马亮亮，吴昊，方秦

（1. 同济大学土木工程学院，上海 200092；2. 陆军工程大学，江苏南京 210007）

1995 年美国俄克拉荷马州联邦大楼恐怖爆炸和“911”恐怖袭击事件后，国内外对建筑结构抗爆研究的关注提升到了一个新的高度。现场爆炸试验是最为有效和直观的手段，但存在周期长、耗费资源大、具有一定安全风险且试验结果受环境影响较大等。在空中爆炸自由场和地面爆炸入射场等单一环境中，基于比例距离（爆炸距离与等效TNT 质量三次方根的比值）的（半）经验公式能够快速准确地估算爆炸冲击波的各项特征参数，如超压、冲量等。但是对于较为复杂的环境，如城市街区，冲击波在建筑物间的反射和绕射等使得（半）经验公式的使用受到限制[1]。随着计算机硬件和大规模商用计算程序的快速发展，数值模拟已经成为一种针对复杂环境爆炸波特征预测的可靠研究手段。

计算模型中网格尺寸对空气中爆炸数值模拟结果影响较大，通常网格尺寸越小精度越高，但由于计算硬件资源和软件性能的限制，网格尺寸无法足够小。因此，选取合理的网格尺寸能够有效地提高数值模拟的计算精度和效率。曲树盛等[2]在研究地铁车站内爆炸波传播时，对沿车站方向不同长度的3 个范围采用了不同的网格尺寸进行模拟。金明[3]在研究新型护栏型防爆墙防护效果及其结构响应时综合考虑计算机性能和计算效率，对TNT 炸药和空气采用5～15 mm 尺寸的渐变欧拉网格。贾亮景[4]基于复杂街区爆炸场景给出了0.8～4.0 m/kg1/3比例距离范围内的自由空气场和1～4 m/kg1/3比例距离范围内地面爆炸反射场的超压和冲量满足15%误差精度的网格尺寸。匡志平等[5]通过定义最佳比例系数确定了0.5～8.0 m/kg1/3比例距离范围内特定比例距离处预测爆炸冲击波参数的最佳网格尺寸。Chapman 等[6]基于有限元差分计算软件AUTODYN-2D 分析了网格大小对爆炸结果的影响，并给出10 mm 以下网格尺寸的修正系数。Shi 等[7]利用较大网格尺寸预测的入射冲量相对准确的性质来修正峰值超压，并在1 和2 m/kg1/3的比例距离处将修正的峰值超压与规范对比验证了其准确性。此外，映射算法是爆炸冲击波数值模拟中常用的算法，如Cowler 等[8]使用AUTODYN 中的Euler-FCT 有限差分求解器，通过将GIS 信息模型导入到AUTODYN 快速建立城市街区模型，并将计算过程分为4 个阶段，每一阶段结束时刻的结果映射为下一阶段的初始条件，实现了对城市中爆炸快速准确的模拟。Löhner 等[9]建议的最佳的映射方法是在爆炸初期运用一维、二维或轴对称模型，并在之后的计算中映射进三维模型中进行计算。

虽然国内外在这方面的研究已有不少，但是在单一尺寸网格敏感性分析中给出的比例距离范围并不是很大[4-5]，并且给出的渐变网格尺寸建议适用的爆炸场景和比例距离范围有限[2-4]，对于网格尺寸效应的修正方法只适用于特定比例距离范围和网格大小[6-7]。为了平衡大比例距离范围内空气爆炸冲击波数值模拟计算效率和精度，同时兼顾软硬件计算能力，本文中使用AUTODYN 软件开展空中爆炸自由场和地面爆炸入射场的单一尺寸网格敏感性分析，确定渐变网格尺寸并与规范结果进行对比验证。同时，针对较大网格尺寸引起的远距离峰值超压预测的误差，提出一种新的修正方法。最后，基于野外足尺房屋爆炸荷载试验对本文中提出的优化网格尺寸和采用的数值模拟映射算法的适用性和准确性进行评估。相关结论可为模拟较大复杂街区爆炸冲击波荷载提供参考。

1 典型工况

建筑结构上爆炸荷载的确定是进行结构动态响应和损伤破坏分析以及结构抗爆设计和加固的前提。针对远距离近地面爆炸后冲击波传播特性以及单栋建筑上爆炸超压分布开展分析工作，相关结论可进一步为复杂街区爆炸工况分析奠定基础。典型远距离近地面爆炸场景如图1 所示，点A、B、C分别为爆炸源、爆炸源垂直地面投影点和建筑物迎爆面。可以看出，爆炸产生的冲击波作用到结构可以分为空中爆炸自由场传播阶段（AB）和地面反射场传播阶段（BC）。需要说明的是：空中爆炸地面反射场与地面爆炸入射场的网格选取原则相似，因此也将图1 中BC段视为地面爆炸入射场。对于空中爆炸自由场，考虑到汽车炸弹、弹药库、危化品储库等爆炸源距地面较近，比例距离范围取0.2～5.0 m/kg1/3。对于地面爆炸入射场，其是地面爆炸反射场分析的基础。实际爆炸中，建筑结构受爆炸影响的范围往往较大，如天津滨海新区爆炸事故中，爆炸能量约为450 t TNT 当量，其房屋建筑保持完好的最小比例距离约为39 m/kg1/3[10]。此外，UFC 3-340-02 规范[11]给出的地面爆炸入射场最大比例距离为39.67 m/kg1/3。因此，对于地面爆炸入射场空气冲击波传播的比例距离范围取0.2～39.0 m/kg1/3。

图1 典型远距离近地面爆炸场景示意图Fig. 1 Schematic diagram of a typical long-distance near-ground explosion scenario

2 网格敏感性分析

AUTODYN 软件是一款显式非线性动力学分析软件，是国际上弹药与爆炸力学等领域研究爆炸、冲击等问题广泛使用的数值模拟软件。采用AUTODYN 商用软件分别对空中爆炸自由场和地面爆炸入射场网格敏感性进行分析，所使用的计算模型如图2 所示。

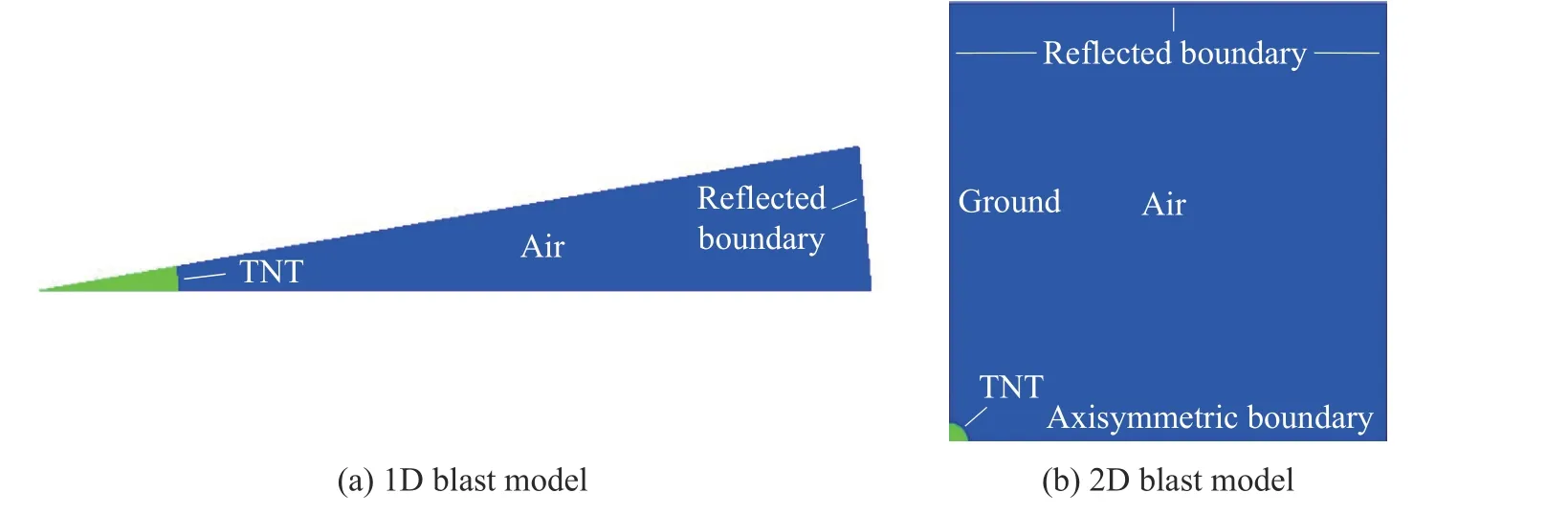
图2 一维和二维爆炸模型Fig. 2 1D and 2D blast models

数值模拟中均采用AUTODYN 内置的材料模型，其中空气为Air 材料模型，采用理想气体状态方程，压力p和比内能e的关系为：

式中：γ=1.4 为空气常数，e=206.8 kJ/kg 为空气比内能，ρ=1.225 kg/m3为空气密度。

TNT 采用考虑后燃烧效应的TNT-2 材料模型，采用JWL 状态方程描述炸药爆轰过程，压力p和内能E及其相对体积V的关系：

式中：A=371.2 GPa、B=3.231 GPa、R1=4.15、R2=0.95 和ω=0.3 为材料常数，初始体积内能E=7.0 GJ/m3。

2.1 空中爆炸自由场

空中爆炸自由场中，为提高计算效率，利用其对称特性，采用一维爆炸模型（图2（a））进行网格敏感性分析。以1 kg 球形TNT 装药为例，采用二维欧拉多物质（Euler 2D multi-material）求解器，考虑到一维爆炸模型流出边界会导致物质流出，影响结果准确性，故将爆炸模型边界设为反射边界，且模型长度取10 m，以确保测点不会受到反射边界的影响。分别考虑7 种单一空气网格尺寸，即：1、2、5、7、10、25 和50 mm。空中爆炸自由场比例距离范围取为0.2～5.0 m/kg1/3，因此，考虑到计算精度和效率，测点选取原则为：在1 m/kg1/3比例距离之前间距取0.2 m/kg1/3，1～5 m/kg1/3比例距离间距取1 m/kg1/3，共9 个测点。从工程设计出发，在软硬件、计算方法、材料参数等其他因素一定的前提下，考虑将数值模拟结果的可信度设为计算精度即爆炸参数（峰值超压和冲量等）的相对误差，并限定相对误差绝对值为15%。

图3～4 分别给出了0.2～5.0 m/kg1/3范围内，各个网格尺寸在不同比例距离下的超压峰值和最大冲量的预测结果与规范的对比结果。可以看出：(1)随着比例距离增大，不同网格尺寸数值模拟预测得到的峰值超压和最大冲量之间的差距逐渐缩小；(2)峰值超压总体预测偏小，最大冲量预测值在小于0.6 m/kg1/3时偏大，随后接近并逐渐小于规范值，原因在于近距离时预测的正相超压持续时间较长；(3)相比于峰值超压，冲量对网格尺寸的敏感性较低。

图3 空中爆炸自由场峰值超压对比Fig. 3 Comparisons of peak overpressures in the free field of air explosion

基于上述分析，表1 给出了空中爆炸自由场中一定比例距离范围内的单一网格尺寸建议值。

表1 空中爆炸自由场单一网格尺寸建议Table 1 Recommended mesh sizes of the free field of air explosion

图4 空中爆炸自由场最大冲量对比Fig. 4 Comparisons of the maximum impulses in the free field of air explosion

2.2 地面爆炸入射场

由于地面爆炸入射场网格敏感性分析需要考虑地面反射，因此选取1 kg 半球型TNT 装药并采用二维爆炸模型（图2（b））。分析的网格尺寸范围为1～500 mm，考虑到硬软件计算能力和精度的要求，不同网格尺寸对应比例距离范围和测点间距见表2。其中不同网格尺寸选取的比例距离范围和测点间距有所差异，主要原因为：(1)爆炸参数（峰值超压和最大冲量）在比例距离较小时变化较快，通常较小尺寸网格适用小比例距离，较大尺寸网格则相反；(2)测点间距越小，网格敏感性分析结果就越准确，但采用更为准确分析结果进行计算，计算效率则会随之降低。

表2 地面爆炸入射场网格尺寸和比例距离对应关系Table 2 Relationship between mesh sizes and scaled distances for ground explosion

相应峰值超压计算结果对比如图5 所示，由于峰值超压跨度过大，故分为两部分并将峰值超压在对数坐标系中表示以便结果对比。可以看出：(1)与空中自由场爆炸相似，随着比例距离增大，地面爆炸入射场超压预测结果与规范计算结果差距逐渐缩小；(2)与规范值相比，随着比例距离增大误差逐渐稳定，这是由于爆炸冲击波的主要频率随着比例距离增大而逐渐降低，同时对网格尺寸的敏感性逐渐降低[8]；(3)相对误差呈现先降低后升高趋势，原因在于，随着比例距离增大，峰值超压对网格敏感性降低起主要作用，相对误差逐渐减小，但在一定比例距离后，峰值超压减小起主要作用，导致误差又逐渐增大；(4) 100、200 和500 mm 网格的相对误差随着比例距离的增大分别接近30%、58%和88%，原因在于，采用这3 种网格尺寸时在比例距离较小处产生较大误差，即便后续网格敏感性逐渐降低也不能使相对误差保持在较小值。故对于200 和500 mm 网格，0～39 m/kg1/3比例距离范围内的相对误差均不满足要求。解决该问题的方法是采用映射方法实现从小尺寸网格到大尺寸网格的递进。

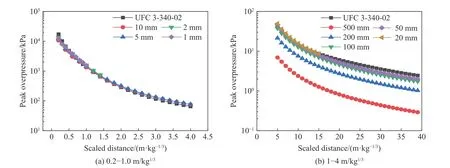
图5 地面爆炸入射场峰值超压对比Fig. 5 Comparisons of peak overpressures for ground explosion

图6 所示为最大冲量对比结果。可以看出：比例距离小于0.4 m/kg1/3时，5 和10 mm 网格得到的误差较大（超过70%），随着比例距离逐渐增大，相应的误差绝对值迅速减小；20～200 mm 网格在比例距离1 m/kg1/3时误差较大，但当比例距离大于2 m/kg1/3时误差绝对值基本都在10%以内；采用500 mm 网格时，随着比例距离增大相对误差逐渐增大。另外地面爆炸时冲量对网格尺寸的敏感性较低。

图6 地面爆炸入射场最大冲量对比Fig. 6 Comparisons of the maximum impulses for ground explosion

由上述分析可以得出地面爆炸入射场在一定比例距离范围内满足精度要求的单一网格尺寸见表3。需要说明的是：(1)由于冲量网格敏感性很低，故主要考虑峰值超压对网格尺寸选择的影响；(2)在比例距离超过10 m/kg1/3后，采用100 mm 网格的相对误差在15%～30%之间，但由于在此比例距离范围内峰值超压数值较小，绝对误差仅在2 kPa 以内，故综合考虑峰值超压的相对误差和绝对误差以及网格敏感性机理，在比例距离大于10 m/kg1/3时建议的网格尺寸为100 mm。

表3 地面爆炸入射场计算单一网格尺寸建议Table 3 Recommended mesh sizes for ground explosion

3 渐变网格尺寸确定及误差修正

前文中给出了不同比例距离范围内空中爆炸自由场和地面爆炸入射场的单一网格尺寸建议值。对于图1 所示场景，如果爆炸比例距离范围较小，单元数量和计算精度允许使用单一网格尺寸时，可以参考上述建议值。若其比例距离范围较大，单一网格尺寸已经不能同时满足算力和精度的需求，需要使用渐变网格，即近距离用小尺寸网格远距离用大尺寸网格。相应AUTODYN 软件提供了映射方法，该方法可以使一个模型的结果映射到另一个模型进行求解，可实现一维到二维、一维到三维、二维到三维、三维到三维模型的过渡[12]，其中各个模型网格尺寸可以不同。对于本文中场景，爆炸波从起爆后到接触地面产生反射前采用一维楔形爆炸模型，地面反射爆炸波传播至结构表面采用二维爆炸模型，之后采用三维爆炸模型，每一阶段的计算结果在到达此阶段规定距离的前一时刻映射为下一阶段的初始条件。本节基于此给出了适用于图1 中典型爆炸场景使用映射方法的一组合理渐变网格尺寸。

3.1 渐变网格尺寸确定

在敏感性分析中并未用到三维爆炸模型，而实际情况中一维和二维模型（见图1）部分占比较小，三维爆炸模型往往占比较高，且由于不能基于对称性简化导致网格数量陡增，此时渐变网格能显著提高计算效率。考虑到软硬件限制，以400 万网格数量为界限，结合地面爆炸入射场网格敏感性分析结果见表3，给出了一组渐变网格尺寸和所适用的比例距离范围见表4。需要指出的是表3 建议的单一网格尺寸最大仅为100 mm，而表4 给出了200 和500 mm 网格尺寸，主要原因为采用渐变网格能够避免大尺寸网格在小比例距离处产生影响。

表4 网格尺寸和比例距离范围对应关系Table 4 Relationship between mesh sizes and the scaled distance

在复杂环境下，准确的爆炸冲击波入射参数是确保反射参数准确性的前提。基于1 kg 半球TNT 地面爆炸，分析表4 给出的渐变网格尺寸在地面爆炸入射场的适用性。爆炸模型为二维正方形爆炸模型，每个模拟阶段对应的模型边长分别为0.5、0.5、1.0、1.5、3.0、8.0、15.0、30.0 和60.0 m。

图7～8 对比了0.2～39.0 m/kg1/3比例距离范围内基于表4 中所给出的网格尺寸，计算得到的峰值超压和最大冲量的计算结果。可以看出：(1)对于峰值超压，比例距离小于5 m/kg1/3即映射到50 mm 网格时，结果吻合较好（相对误差绝对值均小于15%）；当从50 mm 网格映射到100 mm 网格时，误差绝对值与比例距离呈正相关关系，并在比例距离为10 m/kg1/3处误差达到了15.19%；200 和500 mm 网格同样有此趋势且最大误差分别达到44.7%和67.6%。可知表4 推荐的渐变网格对于比例距离小于10 m/kg1/3的峰值超压预测精度较高，比例距离大于10 m/kg1/3后计算结果仍较单一网格尺寸预测结果更好，但误差仍较大，将在下一节对此问题进行修正；(2)对于最大冲量，除了在比例距离0.2、1.6 和1.8 m/kg1/3处误差分别为22.34%、15.48%和16.45%之外，其余误差均在15%以内且多数小于5%，可见表4 推荐的渐变网格尺寸在比例距离0.2～39.0 m/kg1/3全范围内的最大冲量预测精度均较好；(3)注意到图7 中峰值超压在模型间映射设定的比例距离处存在不连续跳跃现象，原因在于冲击波在不同网格尺寸模型中计算产生的误差不同。冲击波从小尺寸网格模型映射到大尺寸网格模型后，从控制测点到下一测点间存在一定距离，需要在更大网格尺寸模型中计算一定时间，由此产生较大变化，且由于在5 m/kg1/3比例距离后测点距离更大，跳跃现象更为明显（见图7（b）中的虚线框处）。

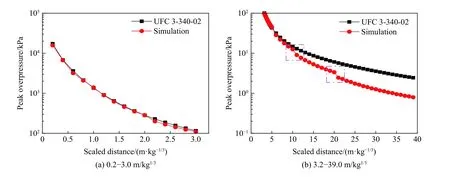
图7 基于渐变网格的峰值超压结果对比Fig. 7 Comparisons of peak overpressures based on gradient mesh sizes

图8 基于渐变网格的最大冲量结果对比Fig. 8 Comparisons of the maximum impulses based on gradient mesh sizes

3.2 误差修正

针对比例距离大于10 m/kg1/3，即大于200 mm 尺寸网格产生的较大误差进行修正。Shi 等[7]提出了一个减小大尺寸网格引起的网格尺寸效应的方法，如图9 所示。首先将真实爆炸超压时程曲线正相部分简化为三角形OAB，接着去掉大尺寸网格超压时程曲线中不合实际的上升段OA，然后采用数值模拟得到的最大冲量In与扣除OA段升压时间后的正压持续时间Tof以得到修正后的峰值超压pm=2In/Tof。上述修正方法存在一些局限性：(1)仅用比例距离1 和2 m/kg1/3的空中爆炸自由场和地面爆炸反射场与TM5-1300 规范[13]的计算结果做了对比验证，在较大比例距离处，由于数值模拟得到的OA段升压时间Tr占总持续时间比较高，导致经过计算后的Tof可能为负数；(2)从修正效果看，对于空中爆炸自由场的峰值超压的修正效果较好，而对地面爆炸反射场的修正效果并不明显，如TM5-1300 规范[13]中对于200 mm 尺寸的网格在比例距离为1 m/kg1/3处反射超压误差绝对值仅从83%降低到80%。

图9 文献[7]峰值超压修正方法Fig. 9 Peak overpressure modification method in Ref.[7]

从图7～8 可以看出，相对于峰值超压，最大冲量受网格尺寸影响较小，预测的结果更为准确。此外，数值模拟中超压上升时间随网格尺寸的增大而增大，而UFC 规范得到的正相超压持续时间更为准确[7]。因此，进一步提出一种适合较大比例距离下的大网格尺寸误差的修正方法。具体修正过程为，首先将正相阶段的超压时程曲线简化为三角形，接着基于数值模拟得到的较为准确的冲量In和UFC 规范计算得到的地面爆炸入射场正相超压持续时间Tu，将峰值超压修正为：

图10 给出了数值模拟得到的比例距离大于10 m/kg1/3时修正前和修正后的峰值超压与UFC 规范计算结果的相对误差，可以看出修正后的峰值超压相对误差值均低于15%。

图10 峰值超压修正方法与计算结果Fig. 10 Predicted peak overpressures with the improved method

因此，对于图1 所示的典型远距离近地面爆炸场景，采用映射算法以及表4 推荐的渐变网格尺寸，并当比例距离大于10 m/kg1/3时采用式（3）的峰值超压修正方法，可使爆炸超压预测结果在0.2～39.0 m/kg1/3比例距离范围内的误差绝对值小于15%，从而得到比较理想的结果。

4 爆炸试验

4.1 试验

如图11（a）所示，Xiao 等[14]开展了全尺寸二层坡屋顶房屋的室外爆炸试验，给出了房屋不同立面和屋顶的反射超压，以及冲击波传播途经特征位置处的入射超压。图11（b）给出了2 次爆炸试验（V2 和V3 工况）中炸药和测点信息，其中炸药高度为0.6 m，爆炸波传播途径中测点共9 个（Ps01～Ps09），房屋上的测点共34 个，测点为对称布置，相应高度见文献[14]。此外，设屋顶测点P14、P18、P21 和P24 所在截面为G-G截面。

图11 爆炸试验概况[14]Fig. 11 Test configuration[14]

4.2 试验验证

4.2.1 试验模拟过程

基于AUTODYN 软件，采用第3 节中的映射方法，整个模拟过程分为3 个阶段。

第一阶段为炸药起爆后爆炸波产生并与地面反射前（图1 中AB段，本文中比例距离约为0.183 m/kg1/3），使用图2（a）一维爆炸模型进行数值模拟，根据第2 节中空中爆炸自由场网格敏感性分析的结果，即表1，采用2 mm 网格尺寸。模型长度取1 000 mm，控制测点在600 mm 处，爆炸冲击波在一维爆炸模型中传播时间约为0.1 ms。

第二阶段为爆炸冲击波接触地面并反射后传播到建筑前（图1 中BC段），采用图2（b）的二维爆炸模型进行分析。试验为近地面爆炸工况，设定网格时需要额外考虑地面反射的影响[4]。为评估此影响，首先得到第一阶段反射前的入射峰值超压为15.727 MPa，对应的规范值为17.106 MPa，相对误差绝对值为8.06%，可认为反射前峰值超压是准确的。之后将第一阶段结果映射到第二阶段5 mm 网格中，测得炸药在地面投影点处反射峰值超压为192.600 MPa，规范值为178.695 MPa，相对误差约为7.78%，故认为5 mm 网格对冲击波反射影响较小，无需调整，需要说明的是，此处数值模拟得到的反射系数约为12.24，超出理想气体情况下反射系数最大值8 且超出规范反射系数，原因在于，炸药在爆轰一定距离后状态方程会由JWL 自动转变为理想气体状态方程，在此模拟过程中状态方程转化比例距离在0.25～0.30 m/kg1/3之间，而炸药距地面比例距离为0.183 m/kg1/3，发生地面反射时炸药状态方程仍为JWL，并未转化为理想气体状态方程，故反射系数较大。表5 给出了该阶段各比例距离范围的网格尺寸、模型大小和网格数量。考虑到V2 和V3 工况在第二阶段比例距离范围最大值均超过5 m/kg1/3，且此阶段在二维爆炸模型中计算效率较高，故在超出5 m/kg1/3比例距离范围内仍采用50 mm 网格计算。此外，为保证映射过程准确，在比例距离为0.5、1.0 和2.0 m/kg1/3处，600 mm高和地面处分别设置控制测点。在爆炸波到达控制测点前停止计算，将结果映射到更大尺寸网格中，进行下一步的计算。爆炸波在二维模型中总传播时间约为31.6 ms。

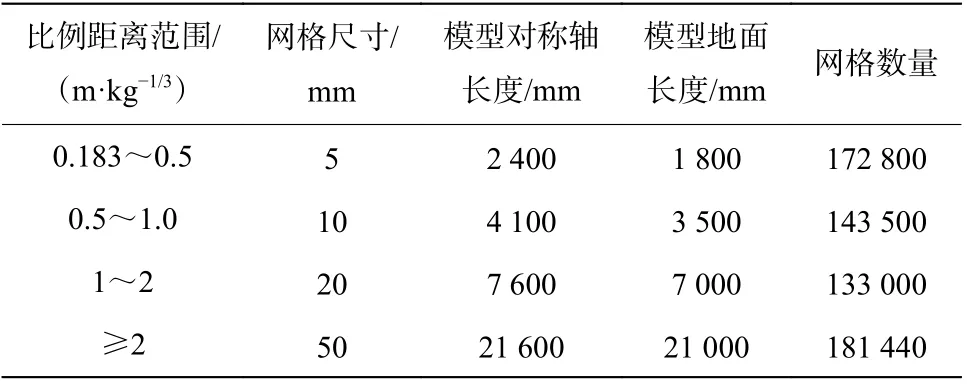
表5 第二阶段各比例距离范围模型数据Table 5 Model data of the second stage at different scaled distances

第三阶段为爆炸波接触建筑墙壁后的反射阶段，此阶段在三维爆炸模型中计算，计算结束时间为70 ms。从第二阶段二维爆炸模型映射到第三阶段三维爆炸模型后的示意图如图12 所示，模型除对称边界和地面边界为反射边界条件外，其余边界均为流出边界。V2 和V3 工况中空气域尺寸分别为28.5 m×17.0 m×12.0 m 和31.0 m×12.5 m×12.0 m，均使用100 mm 尺寸网格，则空气单元数量分别为5.814×106和4.65×106个。房屋模型考虑为刚体模型，有2 种方法实现：(1)房屋所在区域使用未填充材料（unused）单元；(2)使用刚体材料建立房屋模型，前者操作繁琐且对于房屋轮廓处理过于粗糙，故采用后者。房屋模型使用HYPERMESH 软件建模，由于AUTODYN 软件没有内置的刚体材料，使用AUTODYN 内置的IRON-ARMCO 材料代替，其强度模型采用Zerilli-Armstrong 强度模型，求解器采用Lagrange 求解器，Euler 单元和Lagrange 单元之间的耦合方式为完全耦合。

图12 三维模拟阶段示意图Fig. 12 Schematic diagram in 3D simulation stage

4.2.2 结果对比

(1)测点入射超压

V2 和V3 试验工况中爆炸冲击波在空气传播途径中9 个测点（Ps01～Ps09）距炸药的距离相同且两次试验炸药均为35 kg，试验给出了不同工况的平均峰值超压和最大冲量，相应的试验和数值模拟预测结果对比如图13 所示。可以看出：模拟预测结果与试验结果吻合很好，除了Ps02 和Ps05 测点的峰值超压与试验平均值相对误差绝对值较大（分别为34.78%和18.34%），其余测点峰值超压相对误差绝对值都在15%之内，最大冲量相对误差绝对值均在10%以内。由文献[14]可知，Ps02 和Ps05 入射峰值超压相对误差较大的原因为试验测量的偶然性较大，导致试验结果峰值超压平均值偏小。

图13 冲击波传播途径中测点峰值超压及最大冲量Fig. 13 Peak overpressures and maximum impulses at gauges in the path of blast wave propagation

(2)测点反射超压（V2 试验）

图14～15 分别按截面给出了房屋表面测点的峰值超压和最大冲量的试验值和数值模拟预测结果，可以看出：(1) 除P13、P28 和P31 测点，其余测点峰值超压与试验差值较小（相对误差绝对值均小于15%，最大冲量误差均在30%以内）；(2)P13、P28 和P31 测点峰值超压误差分别为15.65%、57.50%和23.36%，最大冲量误差分别为-12.88%、-16.32%和-20.16%，误差较大的原因为数值模拟所建立的房屋模型为简化模型，并未考虑屋檐旁边的钢制密封挡板以及试验中房屋后面的监测站。图16 进一步给出了各截面典型测点的超压时程对比结果，可以看出数值模拟预测精度很好。

图14 V2 各截面测点反射峰值超压对比Fig. 14 Comparisons of reflected peak overpressures in V2 test

图15 V2 各截面测点反射最大冲量对比Fig. 15 Comparisons of the maximum reflected impulses in V2 test

图16 V2 反射超压时程曲线对比Fig. 16 Comparisons of reflected overpressure-time histories in V2 test

(3)测点反射超压（V3 试验）

图17～18 按截面分别给出了房屋上所有测点的爆炸参数（峰值超压和最大冲量）的预测值和试验结果对比，图19 进一步给出了不同截面处典型测点的相应超压时程曲线的对比结果。可以看出：(1)数值模拟和试验得到的峰值超压差别较小，大多数相对误差绝对值小于15%，绝大多数在30%以内；(2)最大冲量预测结果与试验结果差别较大，但除了F-F截面中P15、P16、P22、P23 测点外其余相对误差绝对值均小于30%；(3)F-F截面较其他截面峰值超压和最大冲量的相对误差绝对值均偏大，原因在于试验中采用的压力传感器的量程为35 kPa，比F-F截面峰值超压高出较多，以及F-F截面后监测站的反射作用；(4)P14 相对误差偏大的原因在于模拟中的房屋模型为简化后的模型，将不平整的屋顶简化为光滑的屋顶，另外一个原因是试验中坡屋顶的角度不是严格的36°。

图18 V3 各截面测点反射最大冲量对比Fig. 18 Comparisons of the maximum reflected impulses in V3 test

图19 V3 反射超压时程曲线对比Fig. 19 Comparisons of reflected overpressure-time histories in V3 test

此外，在计算资源和效率方面，本文中的数值计算在PC 端进行，处理器为4 核心，主频3.60 GHz，运行内存16 GB，且由于AUTODYN 软件单次模拟时CPU 占用较低，实际占用率仅10%～30%。整体计算时长约为21.5 h，其中一维爆炸模型计算时长小于1 min，二维爆炸模型计算时长0.4 h，三维爆炸模型计算时长约为21 h，可见使用映射算法可以显著提高计算效率。文献[14]基于LS-DYNA 软件在服务器端使用共计64 核CPU，采用50 mm 网格尺寸的计算时长为2.18 h。可以看出，尽管本文中的数值计算时间较长，但能够在PC 端运行且预测精度满足要求。