基于SPH-FEM 耦合方法的柔性导爆索分离装置爆炸分离过程数值模拟*
2022-12-02史腾达陈福振
史腾达,陈福振,严 红,刘 虎
(1. 西北工业大学太仓长三角研究院,江苏 苏州 215400;2. 西北工业大学动力与能源学院,陕西 西安 710072;3. 北京宇航系统工程研究所,北京 100076)
柔性导爆索爆炸分离装置作为航空航天系统中必不可少的关键部件,具有加工容易、结构简单、成本较低、可靠性高等特点,对其进行研究对航空航天系统中分离装置的设计加工具有重要意义。
柔性导爆索分离装置爆炸分离的物理过程包括:炸药爆炸冲击分离装置、分离板发生变形断裂以及分离板破损后形成碎片飞溅等,分离过程中所涉及的核心科学问题包括流固耦合、固体变形破碎以及碎片运动等。这3 个科学问题与分离装置的变形程度、装置能否起到分离作用以及飞溅碎片对保护罩和箭体是否产生撞击密切相关。因此,要揭示分离过程的机理,就需要对这3 个关键科学问题开展深入研究。
目前对柔性导爆索分离装置爆炸分离过程的研究主要采用实验和数值模拟。在实验方面,主要采用分离装置局部理想模型来研究分离过程,以及用小型炸药试样爆炸实验来研究炸药的能量特性。典型的有:文学军[1]进行了柔性导爆索平板型分离装置的爆炸分离实验,研究了分离板的断裂性能,分离碎片的飞散速度、飞散角以及碎片尺寸;曹雷[2]进行了柔性导爆索的引爆实验,研究了导爆索的物理爆轰性能以及能量输出特性;吴艳萍等[3]设计了柔性多点同步起爆装置,通过实验验证了起爆装置的爆炸输出威力和同步性;赵凯等[4]制作了一种金属柔性导爆索,并测试了不同直径导爆索的爆速及T 型传爆特性;范新中等[5]针对线性分离装置装药量及可靠性评定提出了一种新型工程方法,该方法降低了成本、缩短了研制周期。虽然实验可以揭示真实情况下爆炸分离的过程,但装置搭建耗时耗力,且实验结果具有随机性;此外,由于爆炸过程中能量过大,还存在安全隐患。
为克服实验方法的不足,采用数值方法模拟爆炸分离过程,可以获得该过程的典型细节,再现整个物理过程。对柔性导爆索分离装置的爆炸分离过程进行数值模拟[1,6-10],主要采用LS-DYNA 或AUTODYN中的流固耦合算法。陈敏等[6]通过LS-DYNA 中的流固耦合算法对宇航线式火工分离装置的非线性动态响应过程进行了数值模拟,验证了流固耦合算法对爆炸分离过程的适用性。王瑞峰等[7]在此基础上采用同样的算法对保护罩的破坏过程进行模拟并提出改进方案,通过数值模拟说明了改进方案的合理性。为了深入研究分离装置的破坏机理,宋保永等[8]、卢红立等[9]通过数值模拟得出分离板的破坏包括层裂和拉应力破坏,保护罩为拉伸破坏和剪切强度破坏。戈庆明等[10]采用AUTODYN 软件中的流固耦合算法模拟了特定类型的柔性导爆索切割铝平板的过程,验证了该型柔性导爆索的切割可靠性。以上研究虽然可以得到分离装置的破坏形貌及机理,但对于结构损伤产生的碎片无法进行模拟追踪。
针对以上研究存在的问题,文学军 [1]进一步对平板型爆炸分离装置进行了数值模拟,采用追踪特征单元的方式获得了碎片的速度变化情况。该研究虽然得到了碎片的速度变化,但无法描述碎片与结构之间、碎片与碎片之间的相互作用,且结构损伤后碎片单元上的力将卸载,导致计算精度降低。综上所述,目前对柔性导爆索分离装置的数值模拟多基于商业软件中的流固耦合模块,计算的精度不够高,且对于分离装置的损伤转化以及损伤形成的碎片飞溅过程无法进行高精度的模拟再现。
为解决流固耦合方法在模拟柔性导爆索爆炸分离装置爆炸分离过程中存在的问题,采用SPHFEM 耦合算法不仅可以准确模拟固体结构的变形,还可以计算碎片与结构之间的相互作用。目前已有学者采用SPH-FEM 耦合算法对工程问题进行了研究。一些学者通过将大变形区域设置为SPH 粒子,小变形区域设置为有限单元,二者耦合界面处通过固连接触方式传递力学信息的方式分析了爆炸冲击方面的问题[11-17]。该方法虽然可以更准确地模拟大变形问题,但SPH 方法对于结构整体变形的模拟精度及计算效率较低。在此基础上,林晓东等[18]、胡英国等[19]、米建宇等[20]、方天成等[21]、程兵等[22]通过损伤模型实现有限单元损伤后的删除,并采用该算法研究了磨料水射流破岩,深孔梯段爆破的动力效应等问题。虽然该方法可以删除损伤后的有限单元,但是删除单元的力被强制卸载,很容易出现单元畸变问题。为了保证计算的精度,刘赛等[23]、Karmakar 等[24]进一步将损伤后的有限单元转化为SPH 粒子,并模拟了穿甲燃烧弹侵彻复合装甲和炸药冲击薄板问题,既保证了有限单元的损伤删除,又可以有效避免单元畸变,且后续的大变形仍然可以通过SPH 粒子进行计算。然而该转化算法没有考虑损伤碎片对结构的作用,对于分离板碎片撞击保护罩无法进行有效模拟。
在此基础上,为了克服以上方法在模拟爆炸分离过程中存在的不足,本文中提出一种新型SPHFEM 耦合算法,该算法中不仅包含导爆索模拟的SPH 方法与分离装置模拟的FEM 方法之间的接触算法,同时将完全损伤失效后的单元采用转化算法动态转化成SPH 粒子继续参与计算,转化后的粒子与未转化的有限单元之间采用接触算法计算,搭建一种新的耦合方法框架,实现炸药、结构以及损伤后碎片三者的准确模拟以及三者之间的耦合计算。采用平板型柔性导爆索分离装置和环型柔性导爆索装置两个算例验证新方法的准确性与问题适用性;分析分离板变形断裂及损伤碎片的飞溅过程,得到分离装置表面不同时刻的应力分布、损伤因子的变化趋势、von Mises 应力的变化趋势;并探讨在炸药不同比内能情况下单元的屈服损伤速度。
1 数理模型
1.1 炸药爆轰运动流体控制方程
炸药的爆轰运动通过N-S(Navier-Stokes)方程表述:

式中:ρ 为密度,v为速度,p为压强,g为质量体积力,τ为偏应力张量。
1.2 炸药状态方程
N-S 方程中炸药的爆轰压力p通过JWL 状态方程获得:
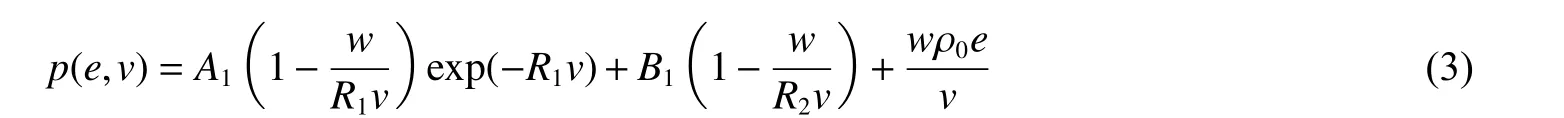
式中:ρ0为炸药初始密度,e为爆轰气体的比内能,A1、B1、R1、R2、w为实验拟合得到的参数。
1.3 分离装置变形运动方程
动力学的基本方程为:
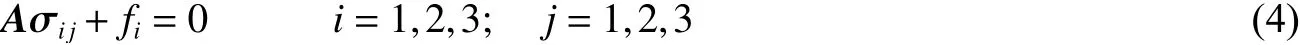
式中:σ 为应力张量,f为单位体积力,A为对坐标的微分算子。
1.4 分离装置本构方程
分离板及保护罩材料模型采用弹塑性模型和Børvik 等[25]提出的含损伤的Johnson-Cook 本构模型,该模型通过流动应力和失效应变描述金属材料的大变形、高应变率等动态力学特征。其流动应力σeq的表达式为:


2 数值方法
2.1 炸药爆轰运动流体控制方程的SPH 离散
SPH 算法是模拟流体运动的一种拉格朗日型粒子方法,通过使用一系列任意分布的粒子来求解具有各种边界条件的积分方程或偏微分方程。SPH 方法通常通过核函数插值实现场变量的插值,通过粒子近似实现对核函数估计积分表达式的粒子离散。
采用强洪夫[26]提出的完全变光滑长度SPH 方法,对炸药粒子及FEM 损伤转化后的粒子的运动进行数值模拟,离散方程组如下:

2.2 分离装置变形运动方程的FEM 离散
有限元法是一种针对连续体力学和物理问题的通用数值求解方法。采用Galerkin 法对微分方程进行离散,得到有限元方程和动力学运动方程:

式中:K为总刚度矩阵,u为单元节点的位移向量,F为已知的结构载荷向量,a¨(t) 、a˙(t)、a(t)分别表示节点加速度、速度和位移,M、C、K、Q(t)分别表示系统的质量矩阵、阻尼矩阵、刚度矩阵和节点载荷向量。
2.3 新型SPH 与FEM 耦合算法
2.3.1 接触算法
计算过程中,计算炸药与分离装置之间、炸药与损伤后的碎片之间、损伤后的碎片与分离装置之间的接触作用使用接触算法。施加在SPH 粒子和有限元节点上的接触力的计算形式如下:
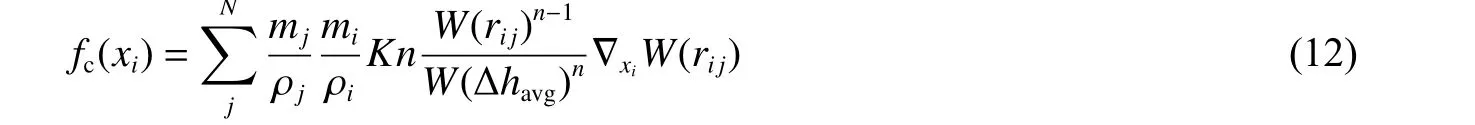
式中:fc(xi)为接触力,rij为粒子间距,W为接触势函数,K、n为用户自定义参数,Δhavg为两个粒子光滑长度h的平均值, ∇xi为i粒子在x方向的梯度。
背景粒子按照未转化的单元节点进行设置,具备SPH 粒子的属性,只能被动地被SPH 粒子搜索,物理量的更新在有限元算法中进行。图1 显示了SPH 粒子与有限单元接触时接触力的施加情况。接触力作为外力分别加入SPH 动量方程和FEM 动力学方程中继续进行求解,其对动量方程和动力学方程的修正形式如下:
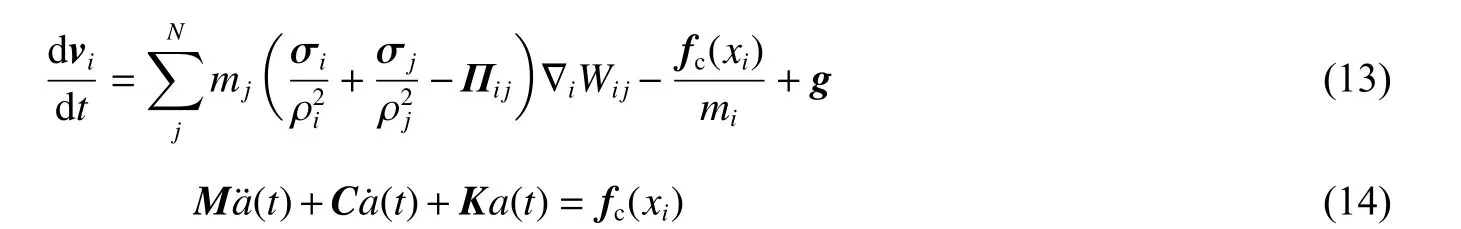
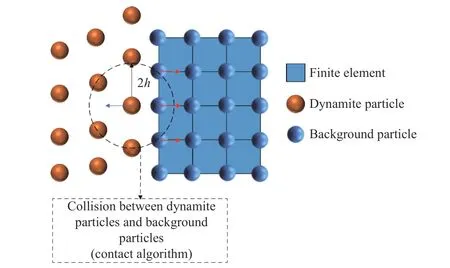
图1 SPH 粒子与有限单元接触Fig. 1 Contact between SPH particles and finite element
2.3.2 转化算法
本文中提出的新型SPH-FEM 转化算法,在有限元计算中添加了含损伤的Johnson-Cook[25]本构模型,以材料是否完全屈服失效作为单元转化判据:

即当损伤值D满足式(15)时,将有限单元转化为SPH 粒子,使得转化条件更加合理。图2 显示了有限单元向SPH 粒子的转化过程。
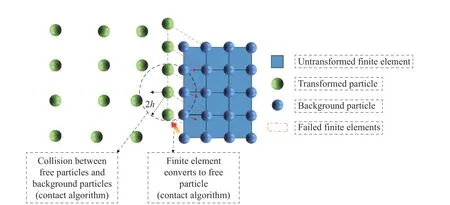
图2 有限单元转化为SPH 粒子Fig. 2 Conversion of a finite element to SPH particles
2.3.3 耦合算法
耦合算法的流程如图3 所示,算法程序读入SPH 和FEM 的模型,并将 FEM 单元转化为背景粒子,SPH 粒子通过临近搜索确定粒子对类型,并对背景粒子施加接触力。背景粒子将接触力信息传递给FEM 单元,接触力作为外力在有限元的动力学方程中进行计算,当计算出的损伤值D>1 时,FEM单元损伤转化为SPH 粒子。SPH 粒子与FEM 单元在计算完毕后,分别进行信息的更新,进入下一个循环。

图3 SPH-FEM 耦合算法流程Fig. 3 Flow chart of SPH-FEM coupling algorithm
本文中的新型SPH-FEM 耦合算法将转化条件由应变阈值修改为损伤值,使得转化条件更合理,转化过程更接近实际,得到了更准确的模拟结果。
3 平板型柔性导爆索爆炸分离问题的三维数值模拟
3.1 计算模型
柔性导爆索平板型分离装置结构平面图如图4(a)所示,分离装置的模型采用Hypermesh 软件建立,如图4(b)所示,蓝色模型右上部分为保护罩,其物理意义是保证炸药在爆炸过程中箭体不受到冲击破坏。模型尺寸除厚度外均在图中进行标注,沿纸面方向向内的厚度为1 m;红色模型为导爆索炸药粒子,其SPH 粒子离散模型如图5(a)所示,粒子数为1239,分离装置的有限单元离散模型如图5(b)所示,有限单元总数为321440。为对比平板型分离装置不同位置处的屈服破坏速度,选取5 个不同位置处的单元进行追踪,具体位置如图4(b)所示,其中位置A位于保护罩上部,位置B位于保护罩右部,位置C位于保护罩半圆边界处,位置D位于分离板中间的削弱槽顶点处,位置E位于分离板右部。

图4 平板型分离实验装置及模型Fig. 4 Plate-type separation experimental device and model
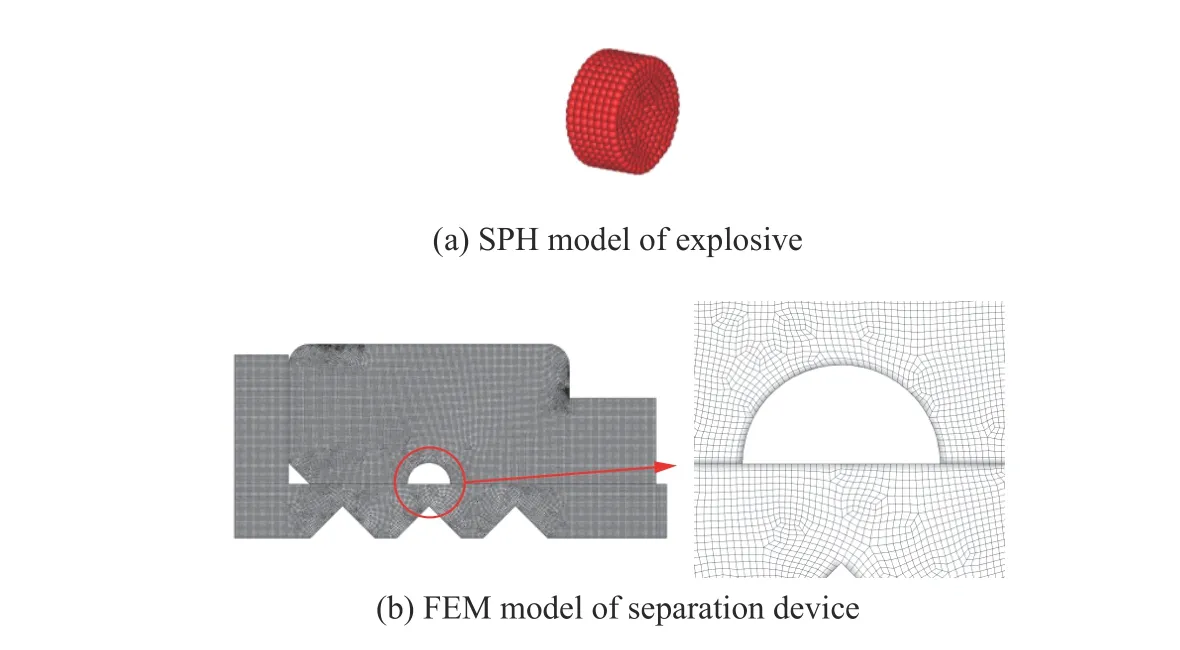
图5 分离装置和炸药的离散模型Fig. 5 Discrete models of separation device and explosive
计算中,炸药在3 种工况下的JWL 状态方程参数见表1,采用点起爆方式,起爆点坐标为(18.0 m,1.0 m, 6.0 m);分离装置采用含损伤的Johnson-Cook 本构模型,材料参数见表2。在保护罩与分离板右侧施加约束,保证变形后结构稳定。

表1 炸药的JWL 状态方程参数Table 1 Parameters of JWL equation of state for explosives

表2 分离装置的参数Table 2 Parameters of separation device
3.2 计算结果
3.2.1 实验对比图
图6 是模拟计算获得的柔性导爆索平板型分离装置破坏后与实验结果的形貌对比图,可以看出,两者在破坏断裂形貌上吻合较好;图7 为模拟计算与实验的分离板左端破坏弯曲程度的对比线图,可以看出,二者的趋势吻合良好。图8 是计算获得的碎片位移-时间曲线与实验拟合得到的曲线对比,由于碎片的飞行速度与结构、炸药装药量等相关,选取3 种不同工况对碎片位移进行研究,3 种工况的位移-时间曲线如图8(a)所示:转化为碎片后曲线趋势与实验结果与图8(b)一致,均为匀速运动;随着炸药初始比内能的增大,碎片的速度随之增大,位移也随之增大。通过计算结果图与实验图的对比分析,验证了该方法在计算爆炸分离问题上的有效性。

图6 计算和实验的断裂弯曲形貌对比Fig. 6 Comparison of calculated and experimental bending fracture morphology
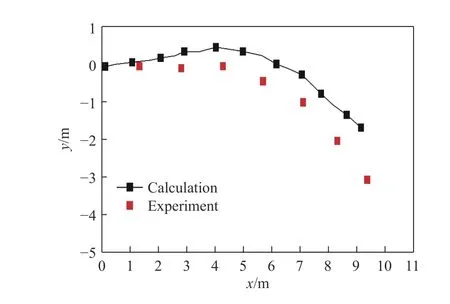
图7 断裂弯曲曲线对比Fig. 7 Comparison of fracture bending curves

图8 计算和实验的碎片位移曲线对比Fig. 8 Comparison of calculated and experimental fragment displacement curves
3.2.2 装置表面正应力分布
平板型分离装置的数值模拟中,随着炸药在分离装置半圆形洞内发生爆炸,炸药粒子撞击壁面,图9 给出了炸药起爆过程中,分离装置保护罩处正应力的分布情况。从图9 可以看出:导爆索起爆后,很快产生爆轰冲击波并迅速作用于分离装置壁面,由于炸药位置影响,半圆形空槽处所受冲击力最大,最先产生正应力;随着爆炸的进行,正应力以应力波的形式由空槽处向四周传播,碰到边界后产生回弹。

图9 不同时刻装置保护罩正应力分布Fig. 9 Normal stress distribution of protective cover at different times
3.2.3 不同位置及不同工况下损伤因子变化曲线
图10(a)给出了5 个不同位置处损伤因子随时间变化的曲线。从图10(a)可以看出,随着爆炸的进行,位置C、D处的单元均达到屈服破坏,即损伤因子为1,位置A、B、E处的单元并未达到屈服状态,即损伤因子小于1;位置D处的单元损伤速度较其他位置明显更快,这是由于位置D处于削弱槽顶点处,在爆炸过程中,削弱槽处的单元会产生应力集中现象,导致单元更快达到屈服状态,进而产生破坏;位置C处的损伤速度较位置A、B、E处的明显更快,这是由于导爆索位于半圆形开口处,导爆索起爆过程中,对位置C处的冲击力较位置A、B、E处的更大,造成位置C处的单元更快达到屈服状态;位置E处的损伤因子较位置A、B处的增加速度更快,这是由于位置E更靠近削弱槽与导爆索,爆炸过程中受到的冲击力大于位置A、B。结合各个位置处的曲线可得:削弱槽顶点处单元屈服损伤速度最快,非削弱槽处单元屈服损伤速度与距导爆索、削弱槽的距离成反比。

图10 损伤因子随时间变化的曲线Fig. 10 Variation curves of damage factor with time
对3 个工况下同一单元的损伤速度进行对比分析,工况参数见表1;图10(b)给出了3 种工况下位置D处的单元的损伤因子随时间变化的曲线。由图10(b)可以看出,随着炸药初始比内能的增大,单元达到屈服所需的时间缩短,屈服损伤速度增大;随着比内能的增大,炸药粒子获得的压强增大,其对装置壁面的冲击力增大,削弱槽顶点处单元的应力集中更明显,导致单元更快损坏。
3.2.4 Von Mises 应力变化曲线
图11 为中间削弱槽顶点D处节点的von Mises 应力随时间变化的曲线,从图11 可以看出,von Mises 应力随时间呈现震荡上升趋势,产生该现象的原因主要有两方面:第一,爆轰冲击波在结构中传播,到达材料边界后出现回弹,导致节点处受力方向改变,这是出现上下震荡的原因;第二,当节点受到外界作用力时,本构模型将产生相反的力维持结构的形状,这是震荡存在峰值的原因。当节点所在单元达到屈服状态破坏后,节点转化为SPH 自由粒子,在SPH 算法中继续进行计算,因此有限元算法中的von Mises 应力保持在转化瞬间的值不变,曲线表现为直线并保持不变。

图11 位置D 处von Mises 应力随时间变化的曲线Fig. 11 Variation curve of von Mises stress at position D with time
4 全环型柔性导爆索爆炸分离问题的三维数值模拟
4.1 计算模型
以文献[1]中的头罩分离实验装置为原型,此装置需要实现头罩与箭体以及2 个半罩之间的分离。2 个半罩与箭体之间分别通过限位铰进行连接,环向部分装有4 根柔爆索。2 个方向的柔爆索通过L 形接头进行连接,L 形接头可以同时起爆3 根呈T 型排布的柔爆索。共安装了2 个L 形接头,并同时点火。
分离装置的有限元模型采用Hypermesh 建立,如图12(a)所示,装置上半部分为头罩,头罩上部外环半径12 m、内环半径10 m,下部外环半径10 m、内环半径8 m,削弱槽厚度为0.5 m;中间部分削弱槽厚度为0.5 m;装置下半部分为箭体,箭体外环半径10 m,内环半径8 m,有限单元总数105771;导爆索的炸药粒子沿削弱槽方向排列,其SPH 模型如图12(b)红色粒子所示,粒子数2718。为对比装置不同位置处的屈服破坏速度,选取5 个不同位置处的单元进行追踪,具体位置如图12(a)所示,其中位置F位于头罩非削弱槽处,位置G位于环型削弱槽与竖型削弱槽交界处的竖型削弱槽上,位置H位于环型削弱槽与竖型削弱槽交界处的环型削弱槽上,位置I位于箭体上部,位置J位于箭体下部。

图12 分离装置和炸药粒子的离散模型Fig. 12 Discrete models of separation device and explosive particle
计算中,炸药的JWL 状态方程同表1,采用点起爆方式,两个起爆点对称分布在竖型削弱槽与环型削弱槽交界点处,坐标分别为(-6.0 m, 0.0 m, 11.0 m),(6.0 m, 0.0 m, 11.0 m),并同时点火起爆;分离装置的Johnson-Cook 本构模型,具体材料参数除D1=25 之外均同表2。在头罩与箭体之间施加局部约束,保证分离后结构的连续性。
4.2 计算结果
4.2.1 实验对比图
图13 是计算获得的碎片位移-时间曲线与实验拟合得到的曲线对比,工况与平板算例相同。从图13(a)可以看出,曲线前半段为单元未失效时的位移曲线,在拐点处单元发生失效,转化为碎片后曲线趋势与实验结果(图13(b))一致,均为匀速运动;随着炸药初始比内能的增大,碎片速度随之增大,位移也随之增大。计算结果与实验结果的对比分析表明,该方法可用于计算爆炸分离问题;柔性导爆索平板型分离装置计算结果表明,该算法具有问题适用性。

图13 碎片位移曲线图对比Fig. 13 Comparison of fragment displacement curves
4.2.2 装置表面正应力分布
图14 给出了炸药起爆过程中,分离装置正应力的分布情况。从图14 可以看出:炸药爆炸后,很快产生爆轰冲击波并迅速作用于分离装置壁面,在起爆起始阶段,起爆点投影处壁面出现应力最大值;随着冲击波沿分离装置内表面向四周传播,在削弱槽处出现应力集中现象,由于头罩处削弱槽上下两端被约束,因此下端约束处应力将首先超过屈服应力,达到屈服状态,环型削弱槽在设置铰链约束处出现应力最大值,将首先超过屈服应力,达到屈服状态;随着单元屈服破坏以及爆炸的进一步传播,破坏处产生更严重的应力集中现象,削弱槽从破坏处向两端逐渐达到屈服破坏。单元屈服后转化为SPH粒子继续进行计算,粒子在运动过程中,受到炸药粒子以及壁面的接触力,位于结构内部的粒子受到向外的接触力,将继续撞击壁面,有一部分粒子会向箭体方向运动,撞击箭体造成箭体损坏;位于结构外部的粒子受到壁面的接触力,并继续向外飞溅。综上所述,在炸药爆炸过程中,应力由起爆点开始沿四周由内向外传播,削弱槽被约束处应力最大,最先达到屈服破坏,削弱槽随后从约束点开始向两端逐渐屈服破坏;破坏后部分碎片会飞向并撞击箭体,导致箭体损毁,因此应在环型削弱槽下方布置防护装置,以保证箭体的结构安全性。
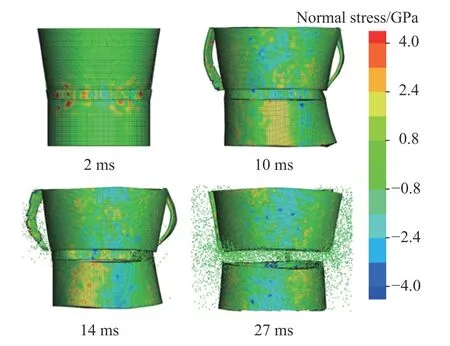
图14 不同时刻装置正应力分布Fig. 14 Normal stress distribution of device at different times
4.2.3 不同位置及不同工况下损伤因子变化曲线
图15(a)给出了5 个不同位置处的损伤因子随时间变化的曲线。由图可知,随着爆炸的进行,位置F、G、H处的单元均达到屈服破坏,即损伤因子为1,位置I、J处的单元并未达到屈服状态,即损伤因子小于1;位置G、H处的单元损伤速度较其他3 个位置明显更快,这是由于位置G、H均处于削弱槽处,在爆炸过程中,削弱槽处的单元会产生应力集中现象,导致单元更快达到屈服状态,进而产生破坏;位置F处的损伤速度较位置I、J处的明显更快,这是由于导爆索位于削弱槽处,竖型与环型导爆索起爆过程中对于位置F处的冲击力较位置I、J处的更大,造成位置F处的单元更快达到屈服状态;位置I处的损伤因子增加速度较位置J处的更快,这是由于位置I更靠近导爆索,爆炸过程中受到的冲击力大于位置J处的。可见,削弱槽处单元屈服损伤速度最快,非削弱槽处单元屈服损伤速度与距导爆索距离成反比。

图15 损伤因子随时间变化曲线Fig. 15 Variation curves of damage factor with time
为探讨炸药比内能不同时装置的屈服破坏速度,选取3 个不同工况对同一单元的损伤速度进行对比分析,工况具体参数见表1。图15(b)给出了3 种工况下位置G处单元的损伤因子随时间的变化曲线。由图可知,随着炸药初始比内能的增大,单元的屈服损伤速度明显增大,达到屈服所需的时间缩短;这是由于随着比内能的增大,炸药粒子获得的压强增大,其对装置壁面的冲击力增大,削弱槽处单元的应力集中更明显,导致单元的损伤速度增大。
4.2.4 Von Mises 应力变化曲线
图16 为中间削弱槽位置H处节点的von Mises 应力随时间变化的曲线。由图可知,von Mises 应力随时间呈现震荡上升趋势,产生该现象的原因主要有两方面:第一,爆轰冲击波在结构中传播,到达材料边界后出现回弹,导致节点处受力方向改变,这是出现上下震荡的原因;第二,当节点受到外界作用力时,本构模型将产生相反的力维持结构的形状,这是震荡存在峰值的原因。当其节点所在单元达到屈服状态破坏后,节点转化为SPH 自由粒子,因此有限元算法中的von Mises 应力保持在转化瞬间的值不变,曲线表现为直线并保持不变。对比平板型von Mises应力曲线可知:von Mises 应力随时间变化趋势为先震荡,后直线。
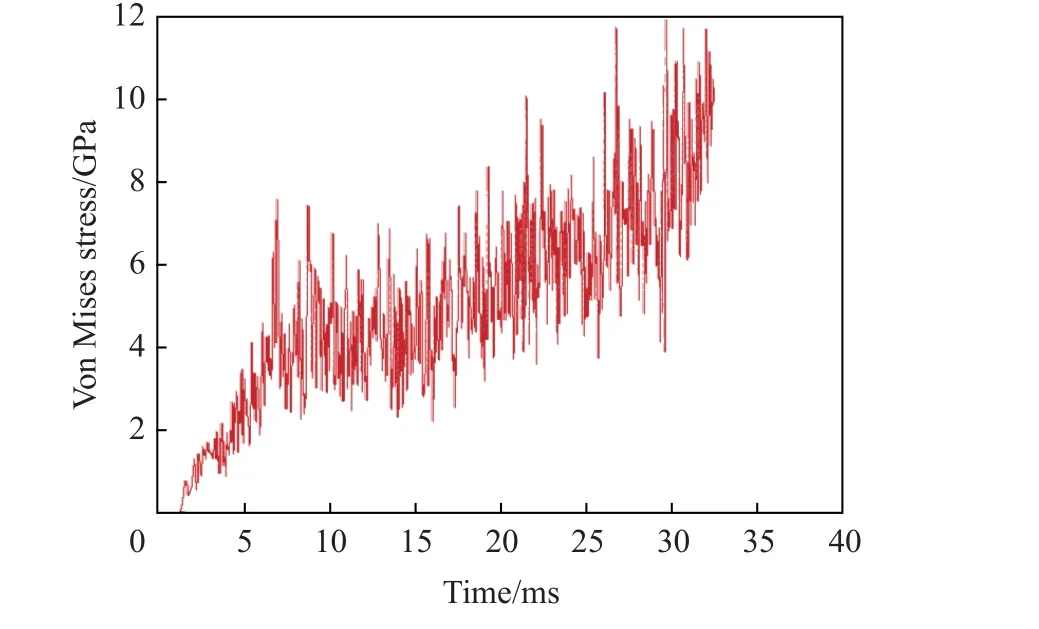
图16 位置H 处的von Mises 应力随时间变化的曲线Fig. 16 Variation curve of von Mises stress at position H with time
5 结 论
提出了一种新的SPH-FEM 耦合方法,并采用新方法对两种柔性导爆索分离装置的爆炸分离过程进行了数值模拟,得到以下结论。
(1) 通过新型SPH-FEM 耦合方法对环型和平板型两种爆炸分离结构的分离过程数值模拟,验证了该方法具有较高的精度和较好的适用性,同时新的方法可以延伸应用于其他类似的爆炸与冲击动力学问题;
(2) 通过数值模拟,发现随着炸药粒子初始比内能的增加,碎片位移的速度增大,单元的屈服损伤速度增大;飞溅碎片会撞击箭体,应在分离板与箭体之间施加保护措施。
