基于风机风向相关系数的风向仪共享控制方法研究

文 坤，万宇宾，胡凯凯，张家友，陈亚楠，李克成

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

近年来，风力发电行业发展迅速，风电技术日趋成熟，行业对风机的可靠性和利用率提出了更高要求。在风机运行过程中，风向仪的探风功能至关重要，其作用相当于人的眼睛。风力发电机组根据其发电特性通常被部署在自然环境条件比较恶劣的山川、戈壁、海洋等处。恶劣天气与极端环境条件极易引起风向仪冰冻、线路老化等问题，从而导致风机故障停机或风向仪测量精度严重失准［1］；而维护人员往往不能及时处理这类故障问题，严重影响风机发电的可靠性和风机的利用率。因此，快速发现并及时处理风向仪故障和失准问题尤为重要［2］。

目前，学者们已针对风向仪的风速和风向校正与预测方法做了许多研究工作。文献［3］提出基于历史运行数据的风向标测量误差校准方法，其采用改进聚类算法（density-based spatial clustering of applications with noise，DBSCAN）清洗数据样本，通过双调和样条插值及发电性能量化等分析方法辨识误差，从而实现风向测量偏差的校正。文献［4］将皮尔逊相关系数用于衡量不同风机之间风速序列的相关性，提出了一种基于人工神经网络的指定风机风速预测方法。根据行业内风速风向共享技术理念，其部分研究方法可用于风速仪故障或信号失准问题规避方法的研究。如文献［4］，采用相邻风机的原始风速序列对指定风机的风速信号进行预测，即可获得指定风机的共享风速信号。但考虑到风机探风精度和发电量提升度与风向信号精准度强相关，可从风向仪风向属性出发，探讨相关系数方法在风向相关性方面研究的可行性。

根据风机风速风向共享技术理念，本文从风向仪风向共享维度出发，利用回归方程法和风向矢量平均法对相邻风机的风向序列进行预处理，并基于相关系数理论，计算得到风向相关系数表，形成缺陷风机的风向共享风机群，最后依据既定共享控制策略将共享风向信号与缺陷风机共享，实现风机避障运行。

1 风机风速风向共享技术

风机风速风向共享技术，是指风机测风设备由于外在或内部原因导致其无法正常工作的情况下，通过一定策略获取其他相关风机的风速和风向信息作为该风机的共享风速和风向信息，从而规避风机因测风设备异常所致故障停机的风险。风机风速风向共享控制原理示意如图1所示。

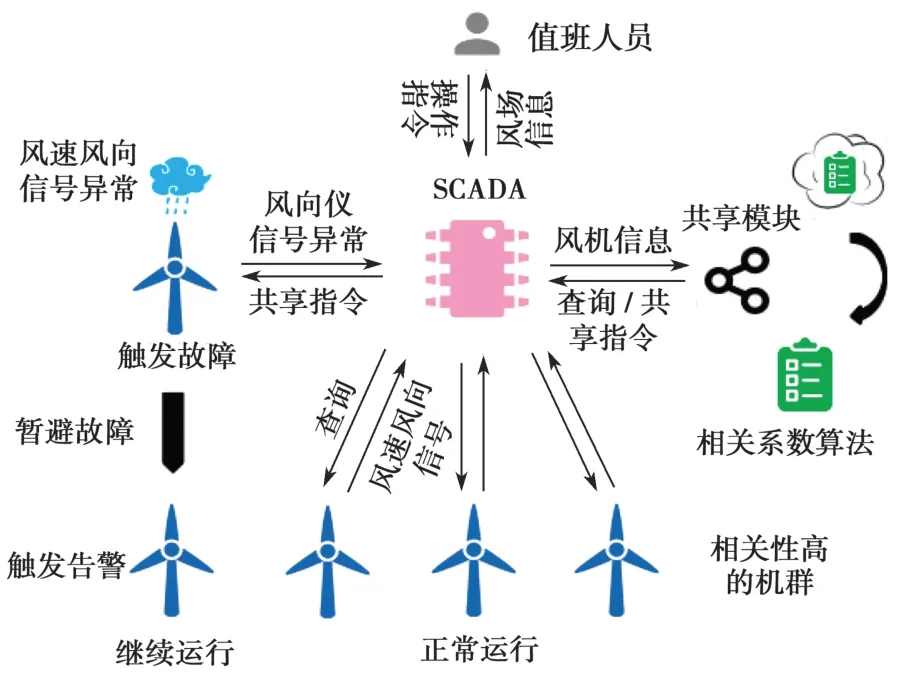
图1 风机风速风向共享控制原理示意图Fig.1 Diagram of wind speed and direction shared control principle of wind turbine

在风场，当某台风机因冰雪、雷暴雨或线路故障导致测风设备故障或测量的风速风向信号出现异常时，该风机会向中控室数据采集与监视控制系统（supervisory control and data acquisition，SCADA）传递风向仪信号异常故障信息。中控室SCADA接收到异常信息后，将风机风向仪异常信息反馈至风速和风向共享计算模块，再由共享计算模块按照既定相关系数列表与优先级规则筛选出与异常风机的风速和风向相关度较高的多台风机，形成风速风向共享机群；同时访问查询这些风机的运行数据信息，获取风速和风向共享计算的基础数据。共享计算模块得到计算所需的基础数据后，通过风速和风向共享算法计算出共享风速和风向序列，并由SCADA系统向异常风机发送共享信息指令。异常风机读取共享风速和风向数据后，暂避测风设备异常故障，继续运行。与此同时，SCADA记录该台风机的测风设备异常故障信息，并将故障信息转为报警信息推送至SCADA界面显示，提醒风场值班人员执行相应操作指令以处理故障［5-6］。

2 风向相关性分析

风向信号的准确度直接关联风机发电量的提升度。为了实现风机风速风向共享控制，本文利用皮尔逊相关系数理论和矢量平均法进行风向相关性分析。

2.1 风向相关系数

皮尔逊相关系数（Pearson correlation coefficient），又称皮尔逊积矩相关系数，是一种用于度量两个变量之间相关程度的线性相关系数［7］。本文定义dr代表共享风机的风向序列，dp代表缺陷风机的风向序列，则可以将两者之间的皮尔逊相关系数定义为

式中：γ——dr和dp之间的皮尔逊相关系数；n——数据样本容量。

根据定义，皮尔逊相关系数γ∈[-1，1]。若|γ|=0，则表示dr与dp之间无线性相关性；若|γ|=1，则表示dr与dp之间完全线性相关；若0＜|γ|＜1，则表示dr与dp之间存在一定程度的线性相关性，并且|γ|越靠近1，则表示dr与dp之间的线性相关程度越高。通常，根据皮尔逊相关等级划分标准，当相关系数满足0.7＜|γ|＜1时，可认为两风向变量间具有较强相关性［8］。

2.2 风向矢量平均法

根据皮尔逊相关系数定义，需要计算风向序列的均值、协方差和标准差。目前，常用的风向序列平均值计算方法包括算术平均法、滑动平均法、频率最高法和矢量平均法。但由于存在风向过零点问题，即“0°～360°”表示法中，0°与360°是指同一个点，当两个变量分别在0°和360°附近时，其平均值为180°，与实际方向相反。在风向仪风向信号共享过程中，这可能导致指定风机的共享风向与实际风向相反，会出现风机反向对风的风险，因此需要合理解决风向过零问题。

在上述4种方法中，算术平均法、滑动平均法均存在风向过零点计算误差较大的问题，而频率最高法则适用于人工气象站统计场景［9］。因此，本文采用风向矢量平均法，即根据同时期风速值计算得到的风矢量可被用来表征风速与风向的密切关系，该方法的统计结果更符合实际情况。

设V表示风速，D表示风向，则风矢量如图2所示。

图2 风矢量Fig.2 Wind vector

图2中，风矢量可用两个分量表示：Vx=VsinD，Vy=VcosD。矢量平均法中，风速可以表示为通过转换，得到合成风速为合 成 风 向 为

由于风向在0°～360°区间变化，故需依据风速分量的不同方向对风向进行判断。本文规定，东、西方向气流，以向东为正方向；南、北方向气流，以向北为正方向。风向判定具体方法如下：

（1）V x＞0，V y＞0时D不变；

（2）V x＜0，V y＜0，或V x＞0，V y＜0时D=D+180°；

（3）V x＜0，V y＞0时D=D+360°；

（4）V x＞0，V y=0时D=90°（E）；

（5）V x＜0，V y=0时D=270°（W）；

（6）V x=0，V y＞0时D=0°（N）；

（7）V x=0，V y＜0时D=180°（S）；

（8）V x=0，V y=0时D不存在。

该方法利用风速与风向信息，计算风向的平均值。由于气流的正、负两个分量存在正负抵消的情况，这就有效解决了平均值计算过程中出现的风向过零点所致的计算误差问题，因此其结果可以代表测风信号随时间和空间变化的实际情况。

3 风向序列的线性回归模型

皮尔逊相关系数理论在数据序列的回归分析中应用广泛。文献［10］中，提出了一种基于相关系数的回归分析方法，该方法利用回归方程将两相关性较高的数据序列进行了近似拟合，相关性越高，数据拟合效果越好。

3.1 基于风向相关性的回归方程

对于本文所研究的风向仪风向序列，可采用基于相关系数的线性回归分析方法［10］推算得到。当两台风机的风向序列dr和dp之间存在密切的线性关系，即表征二者密切程度的相关系数γ较大时，可通过dr的线性回归方程拟合出dp。假设采样样本容量为n，则dp与dr之间的线性回归方程可表示为

式中：——由dr拟合出的缺陷风机近似风向；k，b——线性回归系数；——共享风机风向序列的平均值；——缺陷风机风向序列的平均值；vr——同一时刻的共享风机风速序列；vp——同一时刻的缺陷风机风速序列。

3.2 共享风向序列

假设共享风机的风向序列dr可以准确测量得到，但缺陷风机的风向序列dp无法被直接测量。根据式（3）和式（4）可知，k值和b值的求解需要均值，因此在dr已知而dp未知的情况下，无法通过式（2）直接拟合出共享风向序列。共享风机和缺陷风机的风向序列具有随机性，两者之间的线性相关程度只取决于相关系数的大小而与时间无关。因此，从两条具有较大相关系数的风向序列获取不同时段的风向数据，计算得到的线性系数k和b，其结果应大致相当。据此，通过将共享风机与缺陷风机的风向历史数据代入式（3）和式（4）中，即可求解得到k和b；再将共享风机的实测风向序列d r代入式（2）中，求解得到缺陷风机的共享风向序列。最后，缺陷风机可使用该共享风向序列进行风机探风动作。

综上所述，共享风向序列的探风精准度取决于缺陷风机风向序列与共享风机风向序列的相关程度，相关系数越大，则共享风向序列的探风精度越高。

4 仿真验证

本文实验从宁夏某风场数据中抽取了9台相邻风机的实测风向数据作为实验样本，随机选择3#风机作为风向仪缺陷风机，并按照第3节所述方法利用Matlab进行了仿真研究。在本实验中，考虑风向在一天中存在的周期性，确定以24 h为一个采样时长，每10 min计算一个平均值作为采样点，共选取144个采样点，依此计算缺陷风机与其他8台风机的相关系数。

根据线性相关系数理论，需要确定风向序列是否呈正态分布。从图3所示的实测风向数据分布情况可知，3#风机风向序列具备正态分布特点。

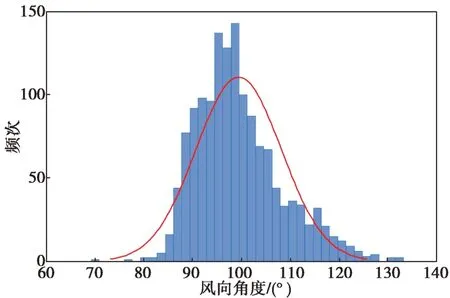
图3 3#风机风向数据的正态分布曲线Fig.3 Normal distribution curve of the wind direction data of turbine 3

随后计算各风机与3#风机之间的相关系数，如表1所示。可以看出，5#风机对3#风机的相关系数最高，4#风机的次之，其他风机的呈依次递减趋势。为了观察不同层次的相关系数对风向序列预测的影响，本实验按照相关性递减趋势，分4个层次选取5#、7#、8#和1#风机作为分析对象。表1中已将分析对象用粗体标记。随后，以每台风机的历史风向数据作为输入，采用前述共享风向计算方法，得到每台风机与3#风机的共享风向序列。

表1 各风机与3#风机之间的相关系数Tab.1 Correlation coefficients between each turbine and turbine 3

图4为5#风机对3#风机的共享风向序列图。图4（a）中虚线为共享风向序列，实线为3#风机风向实测序列。可见，共享曲线能够较好地贴合测量值。同时，通过观察图4（b）中的误差值与临界值比对可知，共享风向序列绝大多数误差值在临界值范围内。该临界值是由行业经验决定。当风机风向与测量风向相对误差在±8°范围以内时，探风精度对风机发电性能影响较小。

图4 5#风机对3#风机的共享风向曲线Fig.4 Shared wind direction curves of turbine 5 to turbine 3

图5～图7分别示出7#、8#和1#风机对3#风机的共享风向序列及相对误差。其中，图5（a）中共享风向序列曲线与实测曲线的贴合程度较5#风机的有所降低，图5（b）中相对误差出现了较多超出临界值的采样点；图6的共享风向序列曲线与实测曲线的贴合程度较图5的有所降低；而从图7（a）可以看出，共享风向序列曲线整体有较大幅度下沉，与实测曲线的贴合程度低，且图7（b）中1#风机共享曲线的相对误差值大部分大于临界值，预测效果差。综合分析图4～图7可以得出，随着相关系数的递减，所得到的共享曲线与实测曲线的贴合程度越来越低。

图5 7#风机对3#风机的共享风向曲线Fig.5 Shared wind direction curves of turbine 7 to turbine 3

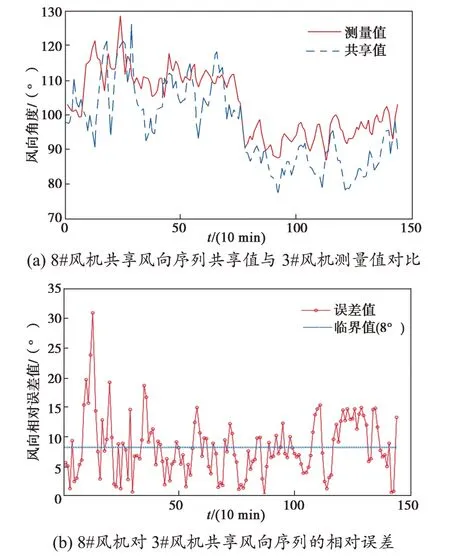
图6 8#风机对3#风机的共享风向曲线Fig.6 Shared wind direction curves of turbine 8 to turbine 3

图7 1#风机对3#风机的共享风向曲线Fig.7 Shared wind direction curves of turbine 1 to turbine 3

随后，根据相关系数列表，计算出各风机对3#风机共享风向序列的累计平均误差和平均相对误差，具体如表2所示。由表2可见，5#风机的平均相对误差最小，为3.49%；4#风机的次之，为3.95%；其他风机的依次呈递增趋势，直至8#和1#风机的平均相对误差超出临界误差值。由此可知，两数据序列相关系数的大小决定共享风向序列的贴合程度，相关系数越大，共享风向序列预测效果越好。

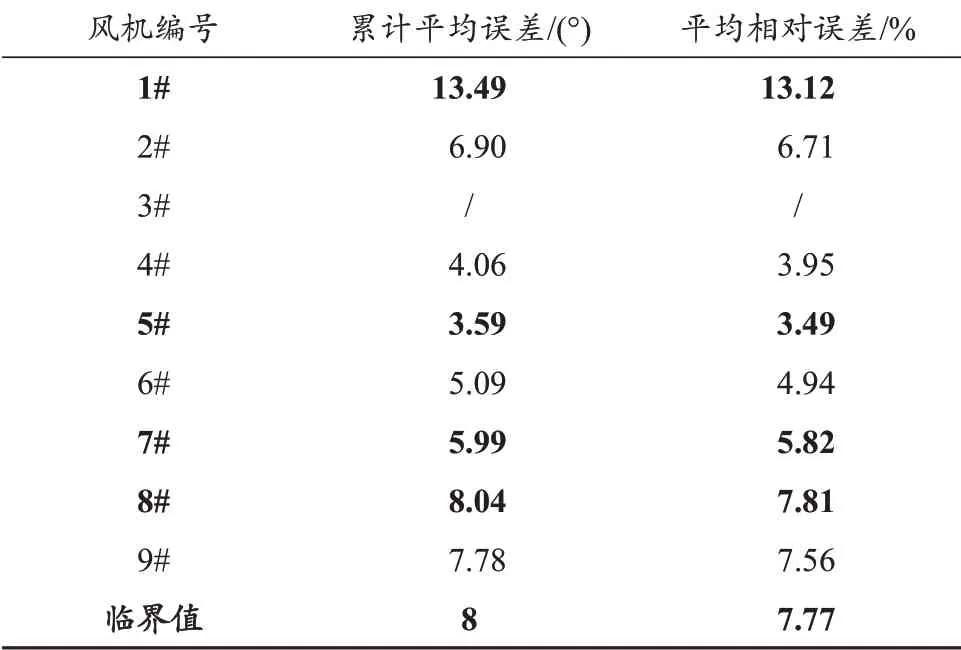
表2 各风机与3#风机之间的相对误差Tab.2 Relative errors between each turbine and turbine 3

通过累计平均误差，可以看出共享风向序列的大体趋势，并获得3#风机的共享机群，如图8所示。5#和7#风机由于其累计平均误差曲线均在临界值以下，因此可以作为3#风机的共享机群；而1#和8#风机则因累计平均值曲线绝大部分超出临界值，因此不宜加入共享机群。确定共享机群后，共享控制模块即可依据既定的共享策略发出共享指令，使缺陷风机维持继续运行。

图8 1#、5#、7#、8#风机累计平均误差趋势对比Fig.8 Trend comparison of cumulative average errors among turbine 1,turbine 5,turbine 7 and turbine 8

5 结语

风向仪测量失准或故障会严重影响风机发电性能和可靠性。本文提出了一种基于风速风向相关系数的风向仪共享控制方法，其基于皮尔逊相关系数理论，利用风矢量平均法，建立了风向仪缺陷风机的相关系数列表，并形成可供缺陷风机使用的共享机群；最后，利用共享机群的共享风向序列，使缺陷风机得以暂避故障，继续运行，实现风机发电性能和利用率的提升。

由于本文所述方法仅从风电机组风向维度实现了风向仪信号共享，而风向仪同时具备风速信号探测功能，虽然风速在风机控制中并不直接参与反馈控制，但极端风速依然会影响风机运行的安全性，因此，在工程化应用中，风向仪共享模式下的风速对风电机组安全性影响可作为下一阶段的研究方向。