改进型时间反转的多用户DCSK系统
2022-12-01张天骐
张 刚,何 平,张天骐
(重庆邮电大学 通信与信息工程学院,重庆 400065)
近年来无线通信在日常工程应用中越来越普遍。由于无线传输的性质,信号携带信息从发送端通过各种干扰传输到接收端,通信质量易受天气条件、传输中建筑物、反射、衰落信道、干扰等影响,故其保密工作及其重要。世界各地研究人员越来越关注混沌信号提升无线通信系统的保密性[1]。混沌通信调制技术分为非相干混沌调制和相干混沌调制,其中利用非相干混沌调制的差分混沌移位键控(Differential Chaos Shift Keying,DCSK)被广泛研究。在混沌通信的研究中,混沌数字调制技术由于自身良好的抗衰落和抗截获特性,非周期混沌信号被广泛地用作信息载体[2-4]。差分混沌键控应用最为广泛。DCSK系统不仅能在多径衰落或时变信道下获得优异的性能,而且易于低复杂度实现[5-6]。在过去十年中,已经在各种通信场景中研究了DCSK系统的性能,例如超宽带应用[7]、双向中继网络编码系统、同步无线信息和电力传输系统、连续移动通信系统、电力线通信系统、协作方案、共存通信系统和多输入多输出系统[8-11]。DCSK用延迟器将比特周期分为两个时隙,第1个时隙传输参考信号,第2个时隙传输信息信号和参考信号乘积的数据承载系列[12-13]。DCSK在两个时隙内,只在后一个时隙内传输一个信息,传输速率较低。为了提高数据速率和误码性能,通过优化参考信号的长度,进一步提高DCSK系统的数据速率和能量效率。张刚等提出了改进型OMU-NRDCSK通信系统的设计与分析[14],利用Walsh码的正交性消除信号间干扰,并且在一个时隙内传输N个信息信号,极大地提升了传输速率。文献[15]提出了正交多载波降噪差分混沌键控(QMC-NR-DCSK)通信系统,通过利用正交调制和希尔伯特变换将系统传输速率提升为MC-DCSK系统的4倍,同时降低了叠加在参考和信息承载信号上的信道噪声问题。文献[16]提出了一种用于非相干混沌通信的频谱高效多进制相关延迟键控(M-ARY CDSK)方案。该系统将QR分解技术应用于不同的混沌信号,完全消除信号内干扰,不仅可以通过将参考信号嵌入到多进制信息承载信号中来提高系统安全性,而且通过多进制调制来获得更好的频谱效率。文献[17]在基于时间反转的多用户差分混沌键控方案中提出了利用时间反转来消除两路信号之间的干扰。并且利用时间反转和延时不同的时间来传输2N个信息比特。但上述系统传输速率低,误码率高。为进一步提高系统传输速率和误码率,笔者首先提出一种改进型ITRM-DCSK(Improved Time Reverse Multiuser-DCSK)方案,在发送端采用时间反转、正交沃尔什码组和在接收端使用滑动平均滤波器消除判决变量中信号间干扰以及减小噪声方差,以此达到降低系统BER的目的。其次利用沃尔什码可同时传输2N个用户信息,达到了两个时隙内传输与原来反转系统N+1个时隙内传输2N个用户信息的效果,大大提升了传输速率。在AWGN信道和多径瑞利衰落信道中研究系统误码性能。通过对系统误码率性能、数据传输的理论推导和仿真分析,发现ITRM-DCSK系统比TRM-DCSK系统性能优越,为将来应用于多用户传输提供了良好的理论基础。
1 ITRM-DCSK方案原理
1.1 发送端
基于时间反转的改进型DCSK的发射端结构如图1所示。
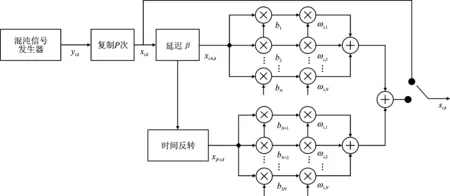
图1 ITRM-DCSK的发送端结构
首先采用混沌信号发生器产生序列长度为R的混沌序列ci,k,其中i表示混沌序列长度,i=1,2,…,R,i表示帧内码元序号,k表示帧序号。再通过Logistic映射和做归一化处理,得到混沌序列yi,k。第k帧混沌序列yi,k的生成过程表达式如下:
(1)
其中,sgn表示符号定数sgn(·)对ci,k进行归一化。
将yi,k与沃尔什码序列ωp,1进行克罗内克积[18]:xi,k=yi,k⊙ωp,1,复制P次,得到长度为β的序列xi,k,作为参考信号在第1个时隙内传输,其中p=1,2,…,P。
沃尔什码是利用阿达马矩阵产生的,阿达马矩阵为元素全为“+1”或“-1”的方阵。多阶阿达马矩阵W2n构造如下
(2)
多阶阿达马矩阵的每一行都表示一段沃尔什码序列。将xi,k延迟β时间后通过时间反转将混沌信号分为两路来传输2N个用户信息比特,并给每个用户分别分配沃尔什码;用加法器将每路的N个用户信息加和在第2个时隙内传输。
图2为ITRM-DCSK和TRM-DCSK第k帧结构的对比图。TRM-DCSK系统帧结构分为等长的一个参考时隙和N个信息时隙。ITRM-DCSK系统帧结构分为两个时隙,前一个时隙传输参考信号,第2个时隙传输2N个信息信号。在帧结构图中,bj、bN+j分别表示前N个和后N个用户信息,j=1,2,…,N。wi.j为第j、N+j个用户所对应的沃尔什码。ITRM-DCSK系统一帧长度为2βTc,相对于TRM-DCSK系统缩短了(N-1)βTc,很大地提升了系统传输速率。
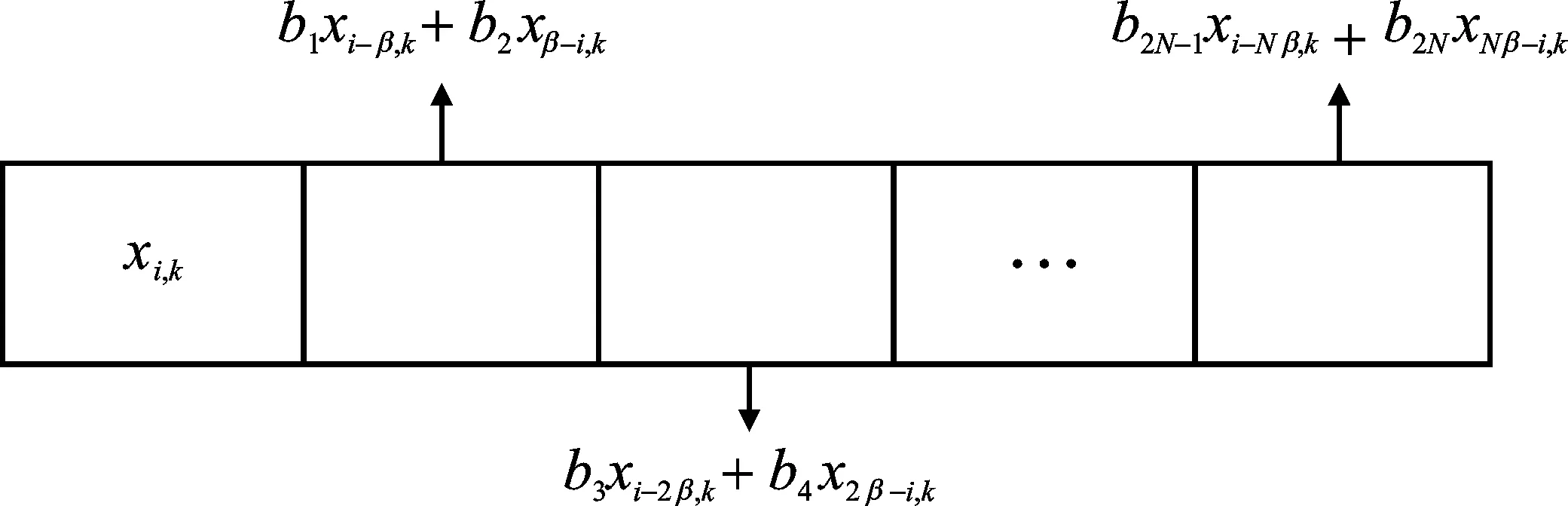
(a) TRM-DCSK帧结构图

(b) ITRM-DCSK帧结构图
定义β=Ts/Tc,Ts为比特持续时间,Tc为码片持续时间,为方便后续理论公式计算,令Tc=1。第k帧的发送信号si,k的表达式为
(3)
其中,j=1,2,…,N,bj、bN+j分别表示前N个和后N个用户信息,wi.j为第j、N+j个用户所对应的沃尔什码。ITRM-DCSK的平均比特能量为
(4)
1.2 接收端
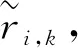

图3 ITRM-DCSK的接收端结构
滑动平均滤波器的结构如图4所示。它的原理是将经过滑动平均滤波器的信号先加再求平均值,得到的信号长度是R,降低了系统解调时的方差,减小了噪声干扰。

图4 滑动平均滤波器结构
第k帧第u个用户和第N+u个用户相关器输出为
(5)
(6)
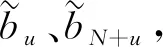
(7)
(8)
2 ITRM-DCSK系统性能分析
2.1 误码率分析
本节分析了该系统在加性高斯白噪声信道和多径瑞利衰落信道下的误码率。因多径瑞利衰落信道较符合信号实际传输信道,故以多径瑞利信道模型为ITRM-DCSK系统传输型。加性高斯白噪声信道是多径瑞利衰落信道的一个特例。多径瑞利衰落信道模型如图5所示。

图5 多径瑞利衰落信道模型
经图5所示的多径瑞利衰落信道后,系统接收信号r(t)的表达式为
(9)

根据经过归一化的Logistic映射的性质可得xi,k的数字特性:E(xi,k)=0,var(xi,k)=1,var(xi,k2)=0,其中E(·)表示均值,var(·)表示方差。根据中心极限定理,当ITRM-DCSK系统的扩频因子β足够大时,对于式(5)和式(6)近似服从高斯分布。所以ITRM-DCSK系统采用高斯近似(Gaussian Approximation,GA)法[19]对ITRM-DCSK系统误码率进行推导和分析。计算误码率均是基于下面条件完成的:
(1) ITRM-DCSK系统等概率发送二进制信息比特{+1,-1}。
(2)ni,k是均值为0,方差为N0/2的加性高斯白噪声。噪声与噪声相互独立,噪声与混沌信号间相互独立。
(3) 由沃尔什序列的特性,使E[ωi,mωi,n]=E[ωi,m]=E[ωi,n]=0,var[ωi,mωi,n]=var[ωi,m]=var[ωi,n]=1 成立。
解调第u个用户信息相关运算值Zu为
(10)
其中,
(11)
(12)
(13)
A项的第1项为有用信号,B项为信号与噪声之间的干扰,C项为噪声间干扰。
解调第N+u个用户信息时相关运算值ZN+u为
(14)
其中,
(15)
(16)
(17)
同前N个用户解调类似,D项的第1项为有用信号,E项为信号与噪声之间的干扰,F项为噪声间干扰。由中心极限定理[20],在β足够大时,Zu、ZN+u近似高斯分布,则可通过均值和方差确定系统误码率。因此,式(5)ITRM-DCSK系统理论的误码率可表示为
(18)
计算Zu的均值和方差:
(19)
(20)
其中,N0/2表示噪声ni,k的方差。
式(6)ITRM-DCSK系统理论的误码率可表示为
(21)
计算ZN+u的均值和方差:
(22)
(23)
将式(19)和式(20)代入(18)式,得到Zu的理论误码率公式,有
(24)
同理,可得ZN+u的理论误码率公式为
(25)
则ITRM-DCSK在多径瑞利衰落信道下的误码率公式为
(26)
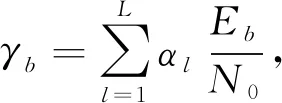
(27)
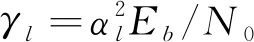
(28)
对于不同信道,γb的概率密度函数有
(29)
其中,
(30)
利用积分公式最终求得ITRM-DCSK系统在多径瑞利衰落信道下的理论误码率公式为
(31)
再计算AWGN中的系统误码率,即当α1=1,α2,…,αL=0时,则有
(32)
2.2 效率和安全性能分析
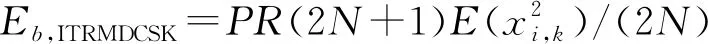
(33)
两个系统的比特能量相同,而传输速率增多N-1倍。
图6分析了Rd曲线,表明ITRM-DCSK相比于TRM-DCSK,在极大程度上提升了传输速率。
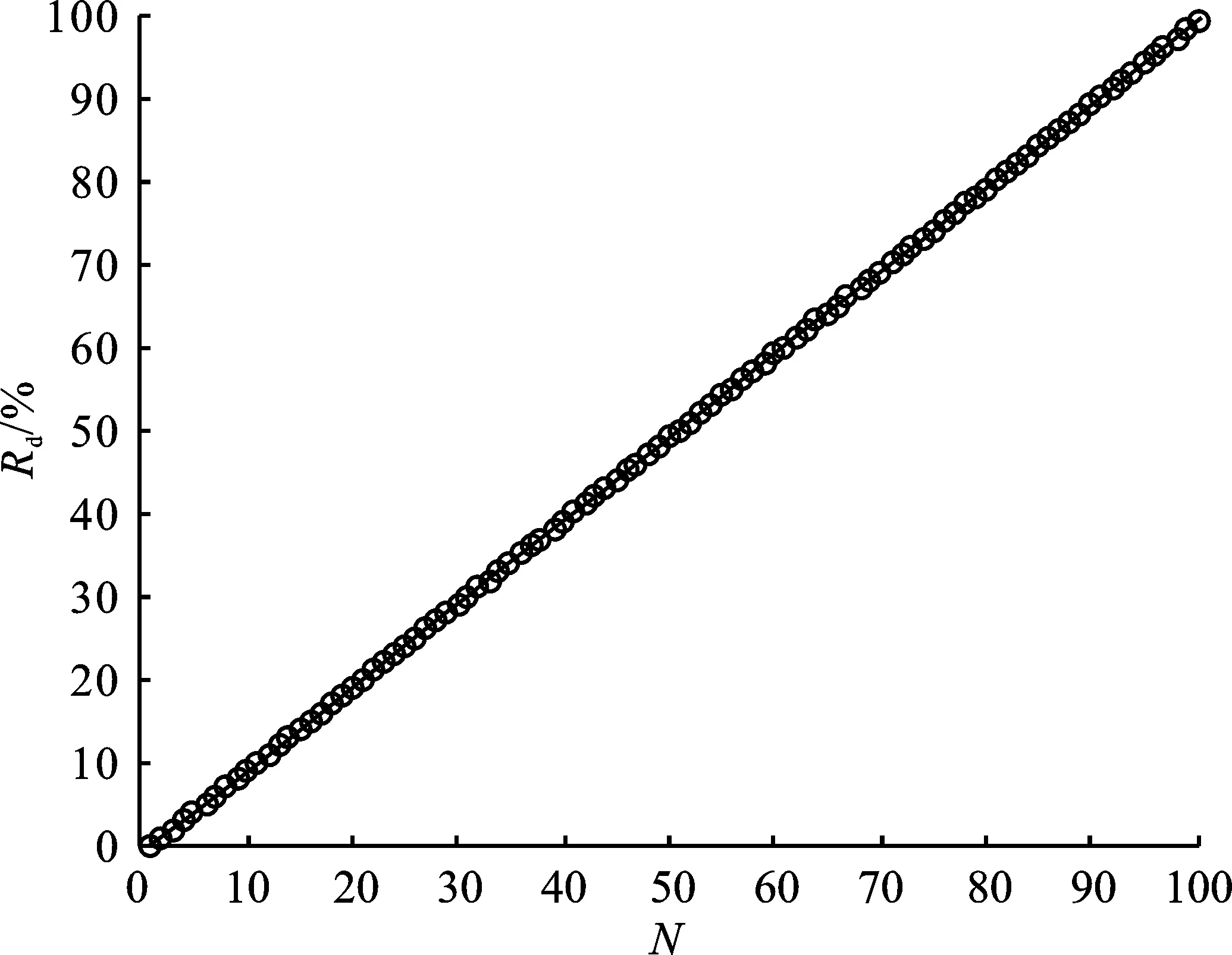
图6 传输速率提升百分比
图7(a)和图7(b)为DCSK和ITRM-DCSK系统的平方幅度谱。图7(a)在DCSK系统频率为比特速率的奇数倍时,其采样平方幅度为0。这是因为DCSK系统采用了T-R传输模型,每比特信号由两段相同长度的混沌信号组成,前一段信号是参考信号,后一段信号用于携带信息信号,故为参考信号的同相或是反相,平方后两段信号完全相同。当频率为系统比特速率奇数倍频点时,平方后的参考信号和平方后的信息信号频谱分量相互抵消,盗窃信息可根据平方幅度谱获取系统的信息比特速率,故DCSK的安全性能差。虽然ITRM-DCSK系统也采用了T-R传输模型,但是,该系统在延迟后还经过了时间反转一个时隙内共传输2N个用户信息,两段信号并无同相或是反相关系。从图中可以看出,ITRM-DCSK系统消除了DCSK系统采样平方幅度是零的现象,增加了采样难度,提高了保密性;得到ITRM-DCSK系统的平方幅度谱具有类噪声性,故其安全性高,适用于通信应用。

(a) DCSK归一化幅度平方谱
3 系统仿真分析
本节对ITRM-DCSK系统在AWGN信道和多径瑞利衰落信道下用Matlab对误码性能仿真分析。仿真结果与理论曲线进行对比,仿真结果与理论曲线吻合良好,验证了式(31)、式(32)推导出的理论误码率公式的正确性。其中蒙特卡罗仿真均为仿真次数为105的情况下平均得到的结果。


(a) AWGN信道
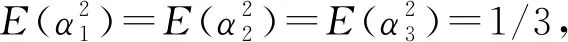

(a) AWGN信道
由图9知存在最佳Nopt使得误码率性能最好。图10研究最佳的Nopt值,在Eb/N0为12、15和18 dB情况下,系统误码率随N值的变化曲线。其他参数β=256,P=2。系统误码率随着Eb/N0的增大而减小。系统存在N较小时,使系统误码率较小,误码性能较好。
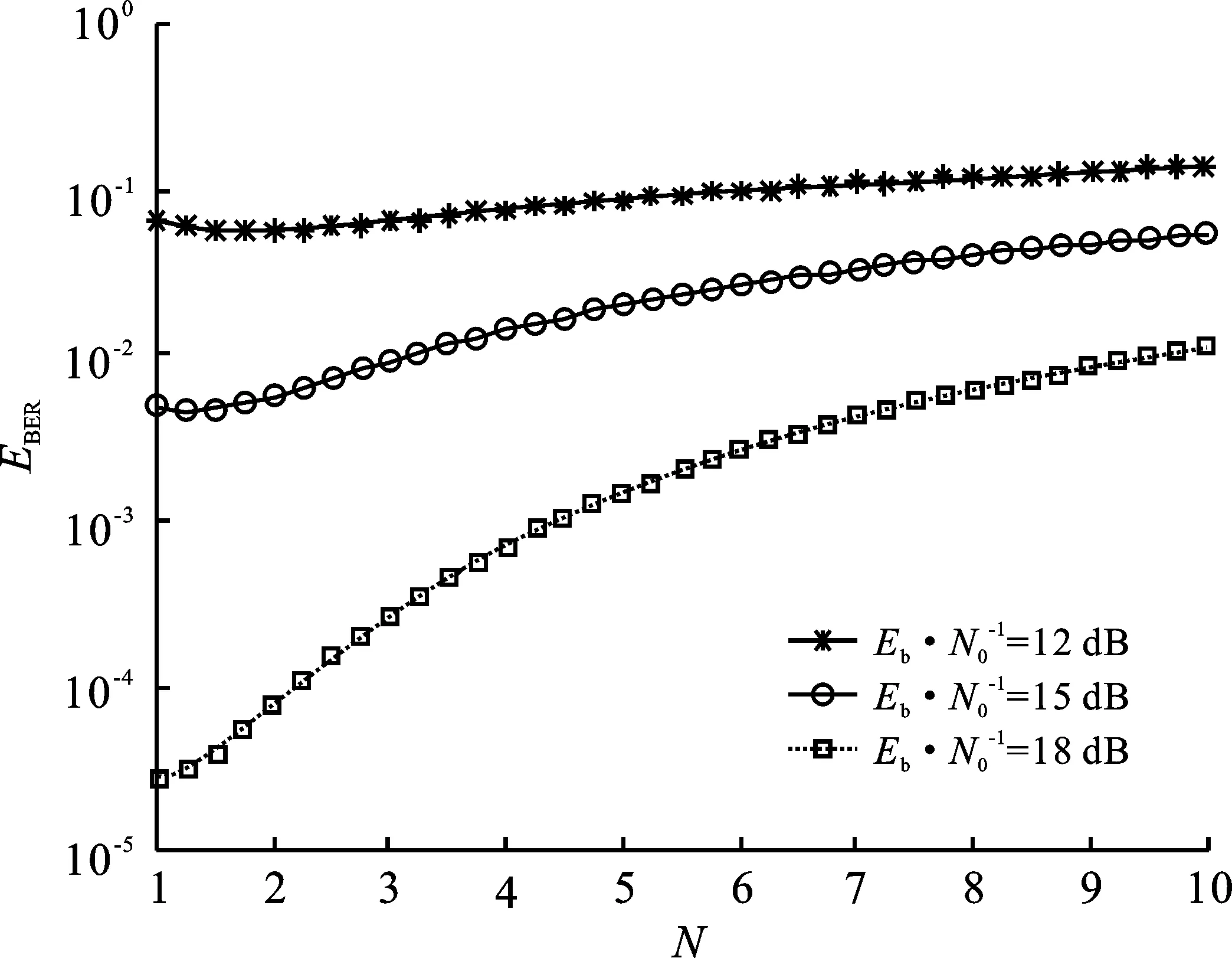
图10 系统EBER随N变化的曲线
图11为Eb/N0分别取8、12和16 dB,其他参数N=2,P=2时,AWGN信道下系统的误码率随β变化的曲线图。当β较小时,仿真值和理论值相差较大,这是因为在用GA法解调时,信号在β较小时不符合高斯分布,误码性能差,导致理论值和仿真值吻合较差。当β较大时,从图11中可以看出,系统误码率随着β的增大,整体的趋势先减小后增大,再趋于一定值。这是因为在β较小时,随着它的逐渐增大,系统的比特能量会增加,则误码率的数值变小。但当β增加到了一定值,当系统的误码率的增加大于比特能量增加带来的好处,又β与系统误码率值呈正比关系,β增大导致系统误码率的增加,整体则呈恶化的趋势,直至趋于一定值。同时,对比了在3种情况下的Eb/N0,当Eb/N0较大时,系统的误码率更好。
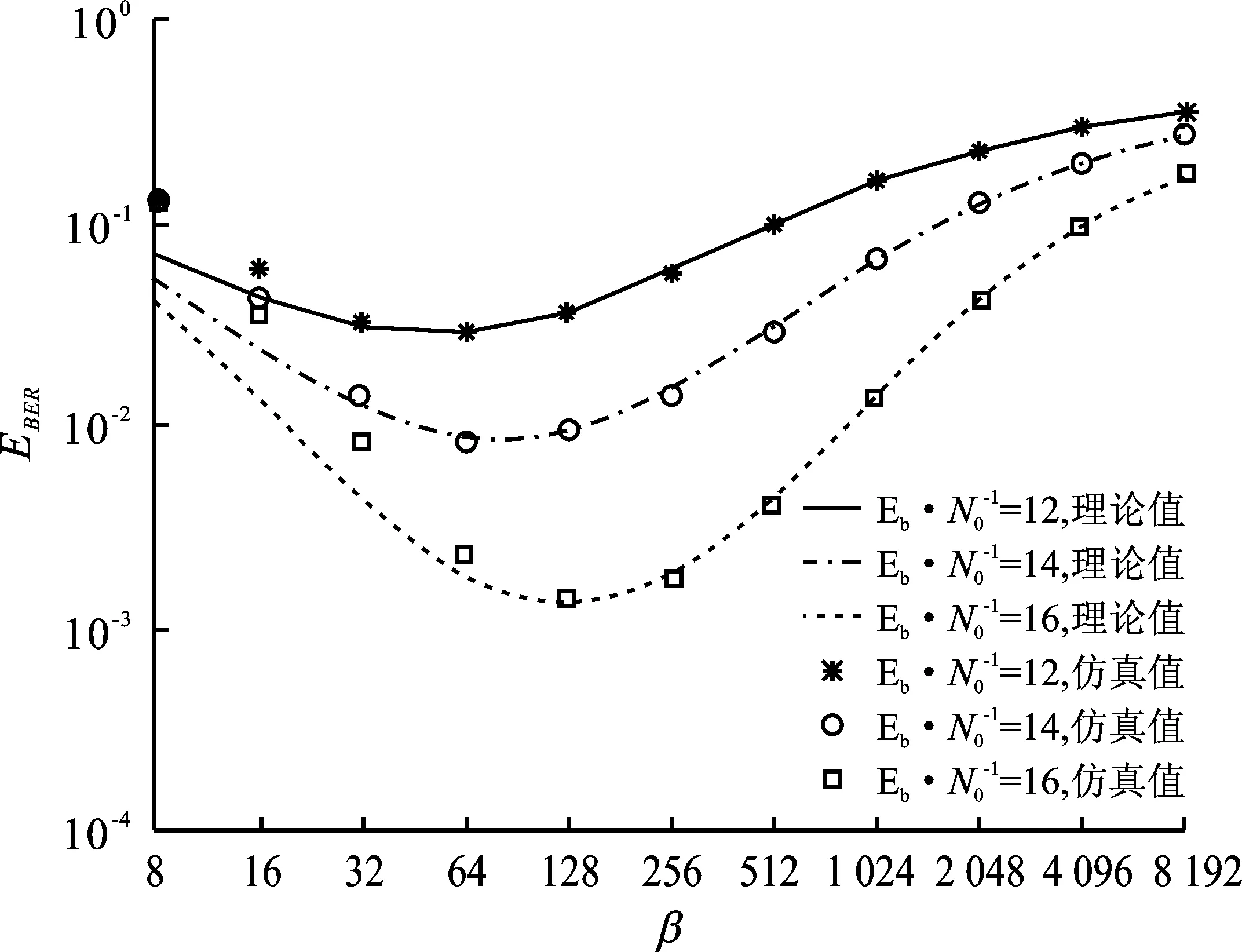
图11 不同Eb/N0下,系统EBER随β变化的曲线
图12为β=256,P=2时,系统误码率随N、Eb/N0变化三维图。在N和Eb/N0变化时,误码率随之变化。当X较小时,即当Eb/N0较小时,随着Y的增加即N增加时,系统误码率先减小后增大。如图12所取点,当Eb/N0=12 dB时,N=2时,系统误码率值最小,误码性能最好。由三维图的颜色深浅度可观察,当Eb/N0较大时,N越小,系统误码率越小。当X一定时,即当N一定时,Eb/N0越大,则误码率降低的趋势越明显。如图所取点,当N=15时,Eb/N0越大,系统误码率值越小,性能越好。

图12 EBER随N、Eb/N0变化的三维图
图13为β=256,N=3时,系统误码率随R、Eb/N0变化的三维图。在R和Eb/N0变化时,误码率随之变化。当Y较小时,即当Eb/N0较小时,R越大,系统误码率越小;当Eb/N0取较大值时,随R逐渐变大,系统误码率则先减小后增大。当X一定时即R一定时,Eb/N0越大,则误码率降低的趋势越明显。
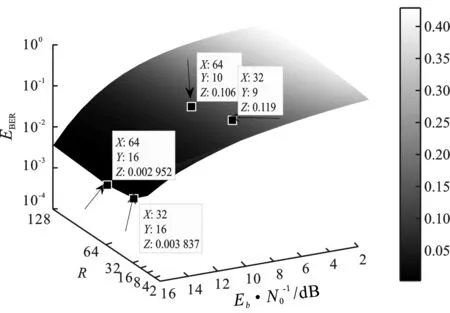
图13 EBER随R、Eb/N0变化三维图


图14 不同路径L下系统EBER的曲线图
图15为该系统在三径瑞利衰落信道中,两种增益情况下系统误码率随Eb/N0变化的曲线。
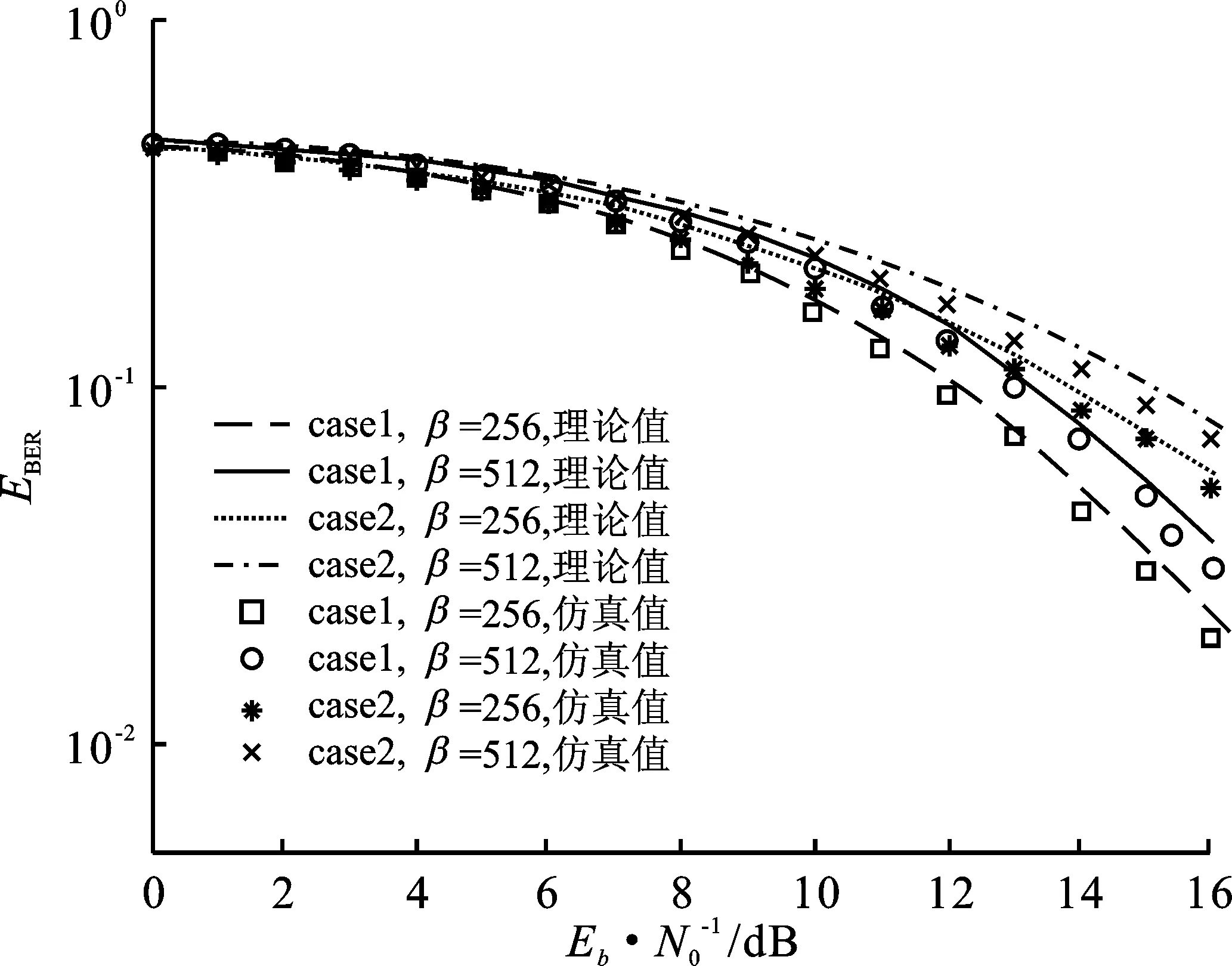
图15 不同信道增益下系统EBER的曲线图
情况13条独立路径的平均能量增益相等,即
(34)
情况23条独立路径的平均能量增益分别为
(35)
仿真结果得出,在等增益的情况下,系统误码率优于不等增益的情况。图14和图15中瑞利衰落信道径数参数如表1所示。

表1 多径瑞利衰落信道参数
图16为N=2,β=512,P=2,4,8的3种情况下,两个系统在AWGN信道和多径瑞利衰落信道下误码率性能对比。可以看出,P越大,ITRM-DCSK系统误码率越小。由于系统在接收端加了滑动平均滤波器,对信号进行了降噪处理,在判决输出变量时噪声干扰减小了,使得错判率减小,且所有的ITRM-DCSK系统误码率值都小于TRM-DCSK系统,故所有的ITRM-DCSK系统误码率性能都优于TRM-DCSK系统误码率性能。

(a) AWGN信道下不同系统EBER的对比图
4 结束语
笔者设计了一个改进型基于时间反转的DCSK,在原有的系统基础上,该系统提高了误码率性能和传输速率,同时传输2N个用户信息。其次,推导了ITRM-DCSK系统在AWGN信道和多径瑞利衰落信道下误码率性能,仿真结果与误码率解析表达式吻合较好,验证了推导的误码率表达式的正确性。且证实它与信噪比Eb/N0和路径数L成正比,与扩频因子β成反比,分析了误码率表达式取决于信噪比、路径数、扩频因子和用户数。计算并对比了ITRM-DCSK系统和TRM-DCSK系统的传输速率,得出ITRM-DCSK在传输速率上有了较大提升。在接收端加入滑动平均滤波器,减小了系统方差,降低了噪声干扰,因而降低了误码率,这具有重要的理论价值和工程意义。论文下一步的工作是在该系统基础上,进一步提出改进的系统,从而使得性能进一步优化。
