基于小波包分解的脑部EIT测量干扰分析与抑制方法研究

梁 文，胡世颉，刘学超，徐灿华，付 峰，杨 滨*

（1.空军军医大学军事生物医学工程学系，西安 710032；2.西安电子科技大学生命科学技术学院，西安 710126；3.空军军医大学西京医院神经外科，西安 710032）

0 引言

电阻抗断层成像（electrical impedance tomography，EIT）是一种以体内组织生理或病理性改变引起的阻抗变化为目标的医学成像技术，其具有无辐射损伤、时间分辨力高、设备性价比高、可进行连续实时成像的优势[1]，目前已应用于肺部[2]、脑部[3]、腹部[4]等器官功能和损伤的图像监测中。然而，在脑部EIT的临床监护中，头部激励-测量电极经常受到体动干扰的影响，导致测量信号失真。体动干扰主要来源于医护人员的治疗、护理操作和患者有意识或者无意识的体动，这都会引起电极接触阻抗的变化，在EIT中表现为明显的伪影，严重降低了图像表征病情变化的能力[5]。

针对上述颅脑EIT的体动干扰，既往研究基于加权相关系数法对单一脱落电极进行检测，并且使用灰色模型预测方法，对电极脱落后的数据进行补偿，以恢复应有的监护图像；同时，使用主成分分析（principal component analysis，PCA）方法和因子矫正法对不同情况下的体动干扰信号进行预处理[6]。在此基础上，最近的一项研究使用循环策略实现多个脱落电极的实时检测，并初步分析了体动干扰对解调后一维数据的影响，使用曲线拟合差分的方法来抑制体动干扰造成的基线变化，将受体动影响期间的数据进行还原处理并优化了数据质量[7-8]。

根据EIT的测量原理，用于成像的边界电压数据是由采集到的激励响应信号经数字解调而来。然而，上述方法对于临床颅脑EIT体动干扰的处理均是针对解调后的电压数据，只分析测量信号保留的幅值信息，而忽略了原始信号的频率特性以及在解调过程中存在的干扰。本研究将基于颅脑EIT原始测量电压信号的解调过程，分析原始测量信号中体动干扰的特征，设计消除体动干扰信号的预处理算法，并对算法进行仿真以及临床试验验证。

1 EIT原始电压信号的测量方法

根据脑组织阻抗频谱特性，颅脑EIT常使用1~200 kHz正弦恒流信号作为激励[9]，该信号注入头部后在头皮表面形成相应正弦电压信号。在16电极系统下，选择一对电极作为激励，同时测量其余各相邻电极对上的电压信号。当激励电极对遍历所有电极后，可得到192组电压信号（对向电极对激励、邻近电极对测量）。EIT系统的测量模块使用模数转换器（analog-to-digital converter，ADC）对每组电压信号进行每周期128个点的采样，采样数据经正交序列数字解调得到用于颅脑EIT图像重构的幅值和相位数据。当系统工作频率较高时，则采用基于异步欠采样的等效时间采样策略对电压信号进行离散化[10]，以降低对高分辨力ADC的性能需求。该策略的原理为：设定采样信号在一定周期内保持不变，信号周期为Ts，2个相邻采样点的间隔时间为Tt，每周期需要完成N个点的采样，现以Tt=13×Ts/N的时间间隔进行采样。当N=128时，则经过13个信号周期后可完成128个不相重复的点的采样，而且第129个点又回到第1个点的相位。这些点与在同一信号周期内以Tt'=Ts/N的间隔采样结果相一致，因而可以对信号进行重建，等效时间采样策略示意图如图1所示。由此可以使用26个信号周期完成2个周期256个点的采样任务。但是体动干扰也会对等效时间采样过程造成影响，因此既往研究仅对解调后的测量数据进行处理是片面的。

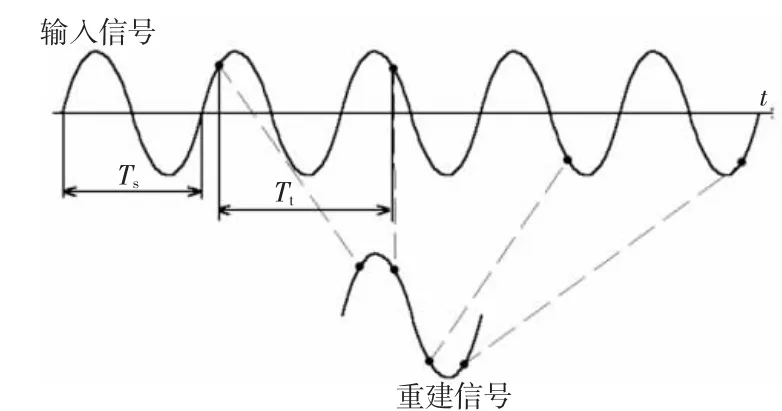
图1 等效时间采样策略示意图

2 颅脑EIT原始测量信号干扰分析和处理方法

2.1 颅脑EIT系统和测量数据

本研究的临床数据来自课题组自研的脑部高精度EIT数据采集系统[9]，该系统可工作在1~190 kHz的频率区间，输出电流在0~1.25 mA间程控可调，使用16电极系统进行颅脑组织阻抗的测量。原始边界电压信号通过一个16 bit采样精度和1 MS/s采样速率的ADC进行采集，数据采集策略为基于异步欠采样的等效时间采样。在临床数据的采集中，将电极带配置于被测者眉弓和枕骨粗隆以上1~2 cm的环面上并用弹力绷带固定（如图2所示），激励电流频率为50 kHz，1 s内完成每帧196组边界电压信号的采集。EIT监测开始后，分别记录因护理操作（如翻身、抬头等）造成被测志愿者体动干扰的数据，待后续分析和处理。

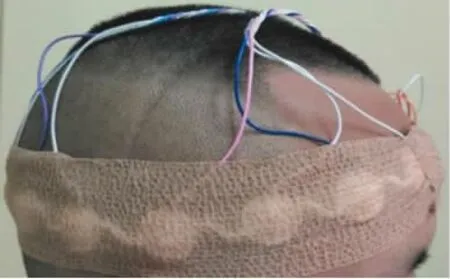
图2 电极系统配置效果图

2.2 体动干扰数据的判别方法

根据原始电压信号的特点，将标准正弦信号与原始电压信号进行皮尔逊相关分析，将相关系数作为判断测量信号是否为干扰信号的参考，其中皮尔逊相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围为[-1，1]，其绝对值越大，则表明X与Y相关度越高[11]。当X与Y呈线性相关时，相关系数ρXY取值为1（正线性相关）或-1（负线性相关），其计算公式如下：

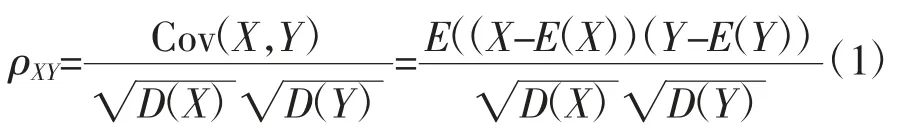
式中，Cov（X，Y）为X、Y的协方差；E（·）为括号内数据的数学期望；D（·）为括号内数据的方差为括号内数据的标准差。

颅脑EIT算法是根据前景帧与背景帧的差分进行重构成像，因此根据背景帧中边界电压的解调幅值A0j，每帧信号的数据集S的计算公式如下：

式中，k为EIT采集的帧数；j为一帧中192个一维曲线值；ω为激励电流的频率；i为每个通道数据的采样值（i=1，2，…，256）。

根据公式（1），前景帧原始电压信号与各标准信号的相关系数集Nj以及解调值差分百分比集Dj的计算公式如下：

式中，j为前景帧的个数，j=1，2，3；Sj为第j个前景帧的原始数据集；S0为模拟的标准信号数据集；Aj为第j个前景帧解调值的集；A0为背景帧解调值的集。根据Nj、Dj的分析确定区分正常边界电压信号和体动干扰信号的相关系数阈值fth。

2.3 受干扰原始电压信号的特征分析和小波包分解

分别对正常和受干扰的原始电压信号进行傅里叶变换，分析主频信号的频谱特征，识别干扰信号所处的频段。利用小波包分解[10，12]剔除干扰频段，重构正常频段的信号，达到滤除干扰信号的目的。其中小波包分解又称为最优子带树结构，是对小波变换的进一步优化[13]，其结构如图3所示。小波包分解的算法思想是在小波变换的基础上，在每一级信号分解时，除了对低频子段进行进一步分解，也对高频子段进行进一步分解。然后通过一个代价函数计算出最优的信号分解路径，并以此分解路径对原始信号进行分解。

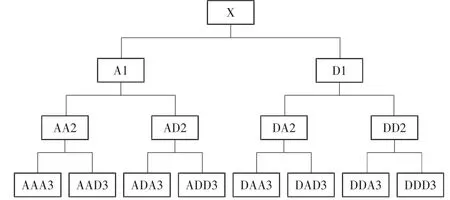
图3 小波包分解结构

可将尺度函数φ（t）记为v0（t），小波函数ψ（t）改记为v1（t），并设滤波器的系数分别为h（k）、g（k），其中h（k）满足∑h（k-2n）h（k-2m）=δn，m（δn，m为脉冲信号，n与m根据所选的小波包种类确认），∑h（k）=对于原来的二尺度关系，可以重新定义递归函数如下：

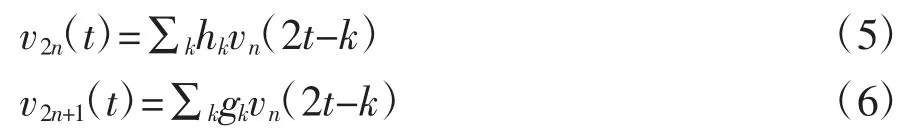
其中，v0（t）与v1（t）满足二尺度伸缩方程：v1（t）=∑kgkv0（2t-k）。

小波包分解采用Mallat算法，根据公式（5）~（6），采用如下递归方程实现：

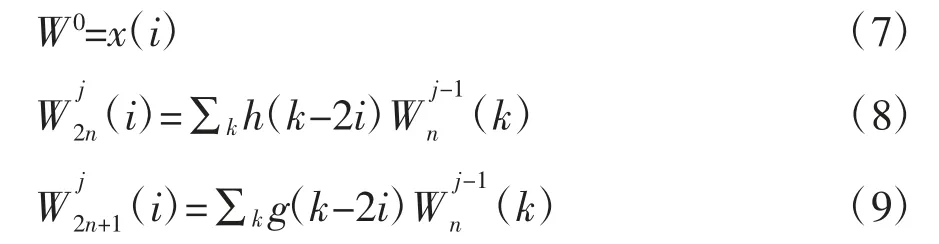
式中，W0为递归方程的初始项；与分别为分解层数为j的偶数项与奇数项；x（i）为原始信号，i=0，1，2，…，N/2-1，n=0，1，2，…，2j-1-1，其中N为采样点数，j为分解层数。

根据上述的递归方程可以将信号正交分解到相对应的频段上。小波包分解算法如下：

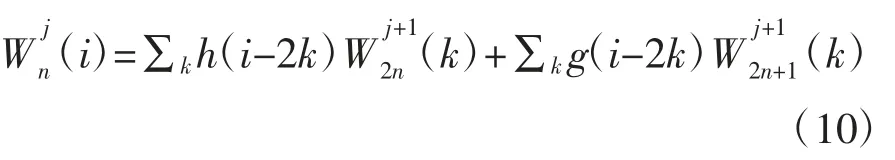
根据小波包分解与重构原理，设计受干扰信号的识别与预处理算法流程如下：

（1）受干扰信号的识别。计算原始电压信号与标准正弦信号之间的相关系数a，根据fth判断是否对信号进行处理。

（2）基于小波包分解的第一步进行预处理。采用db8小波对原始电压信号进行5层分解，共分为32（25）个频段。每个频段的带宽为16 Hz，由于标准的原始电压信号频率在0~16 Hz范围内，使用节点为（0，16）、带宽范围为0~16 Hz的小波包进行重构。针对处理之后的结果，截取中间2个周期的信号作为最终第一步预处理结果。

（3）对第一步预处理结果进行分析、反馈。计算经过第一步预处理后的信号与标准正弦信号的相关系数b，根据fth判断是否需要对第一步处理的结果进行二次处理。

（4）针对反馈结果进行最终干扰抑制处理。当反馈参数b的值小于fth，则判断该组数据失效，并使用背景帧中的数据对该数据进行补充。

3 试验结果及分析

3.1 临床干扰数据判别阈值的确定

本研究使用课题组自研的型号为FMMU-EIT5的脑部高精度EIT数据采集系统实时测量EIT数据。选取5名健康志愿者分别编号为1~5，使其呈仰卧位进行约5 min的颅脑EIT动态监测。其中1~4号志愿者在监测过程中无体动行为，分别采集630帧原始电压信号，5号志愿者首先采集50帧无体动行为时的原始电压信号，然后使其进行翻身和抬头动作，模拟临床护理操作过程，再采集286帧原始电压信号。试验共采集5组共计2 856帧原始电压信号，其中第1~4组以及第5组中前50帧数据为正常测量数据，第5组后286帧数据为受体动干扰测量数据。

根据成像结果，由受体动干扰的原始测量信号解调得到的数据会造成EIT图像有明显的伪影。如图4所示，在相同窗宽下图4（a）因体动干扰出现严重的失真，而图4（b）无明显的伪影。

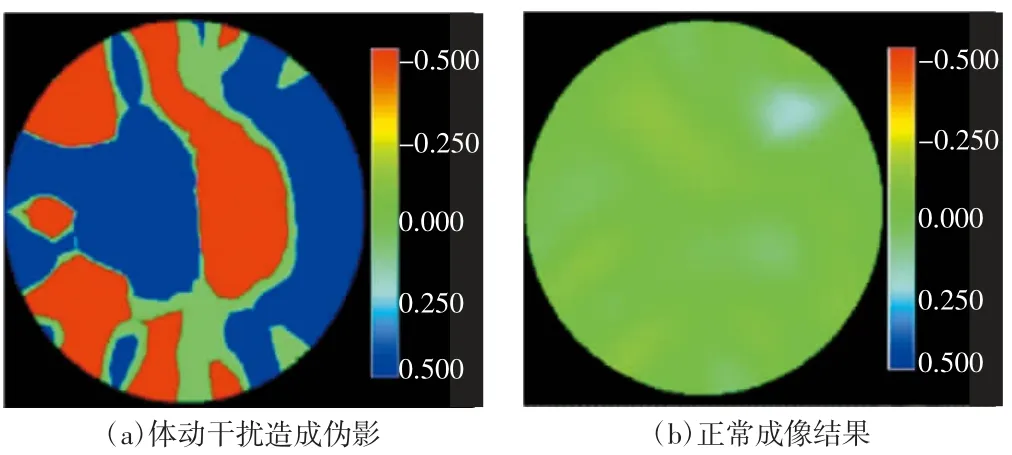
图4 正常与干扰情况下的重构图像结果

在5号志愿者的数据中分别选择3帧正常原始测量数据和1帧受体动干扰的原始测量数据进行分析，计算相关系数集Nj以及解调值差分百分比集Dj，将Dj中所有数据作为x轴、Nj中所有数据作为y轴，画出散点图，如图5所示。其中，图5（a）为整体结果图，5（b）为x轴在[-10，10]区间的局部结果图。由所有志愿者数据的分析结果得出绝大部分的解调值差分百分比集中在[-10，10]，而解调值差分百分比与相关系数之间有一定的关系。因此，将Dj分为集合[-10，10]和[-∞，-10）∪（10，∞]，并归纳出正常原始测量数据和受体动干扰的原始测量数据的相关系数分布，详见表1。同时求取5组数据中正常原始电压信号相关系数的平均值与方差，详见表2。

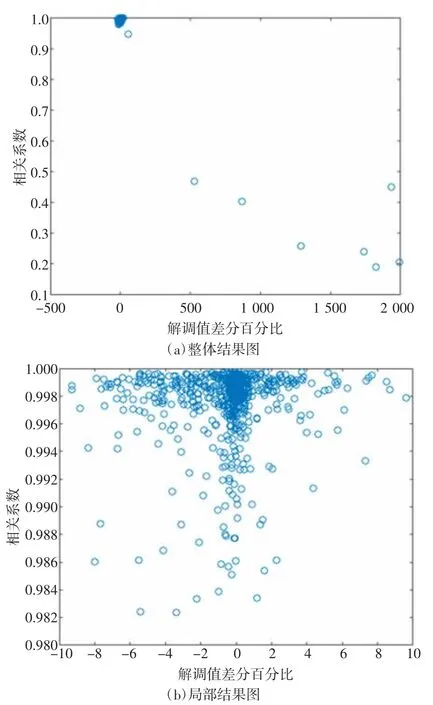
图5 相关系数与解调值差分百分比散点图

根据表1的结果以及正常测量数据帧与受干扰数据帧成像结果可以分析得出：当相关系数达到0.996时，重构图像就可以较好地消除伪影。同时根据表2的结果可以分析得出，正常原始电压信号的相关系数集中分布在0.996周围。因此，将相关系数0.996定义为区分正常信号和体动干扰信号的阈值fth。

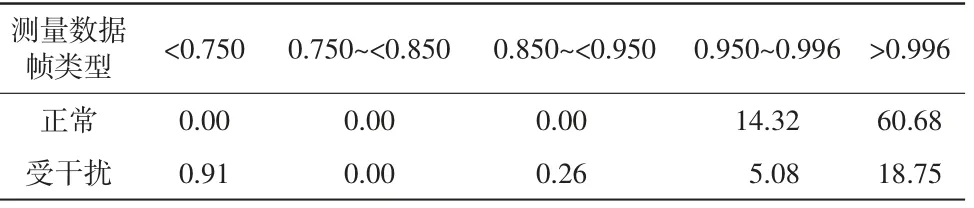
表1 相关系数的分布统计单位：%

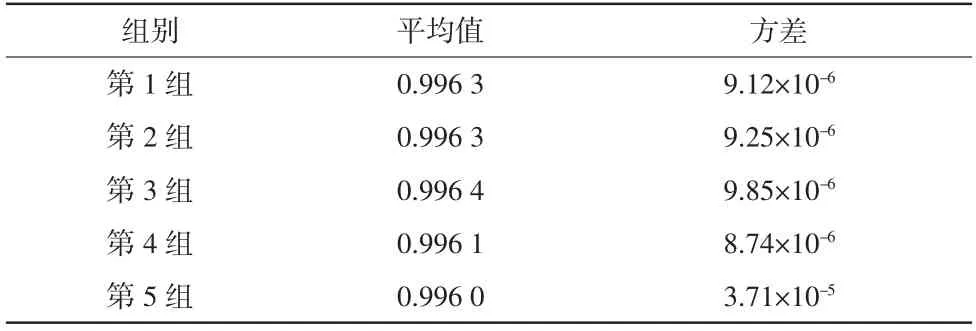
表2 5组数据中正常原始电压信号相关系数的统计学结果

3.2 体动干扰的抑制

（1）体动干扰信号的频谱分析。

对受干扰数据帧中相关系数低于阈值fth的原始电压信号进行频谱分析。结果表明，与标准激励正弦信号相比，等效时间采样的电压数据在波形和频谱上均存在明显干扰。正常与受体动干扰的原始电压信号时、频域特征如图6所示。因此，利用小波包分解方法来区分有用频段与干扰频段，并对低频段的信号进行算法重构，可达到消除干扰的目的。

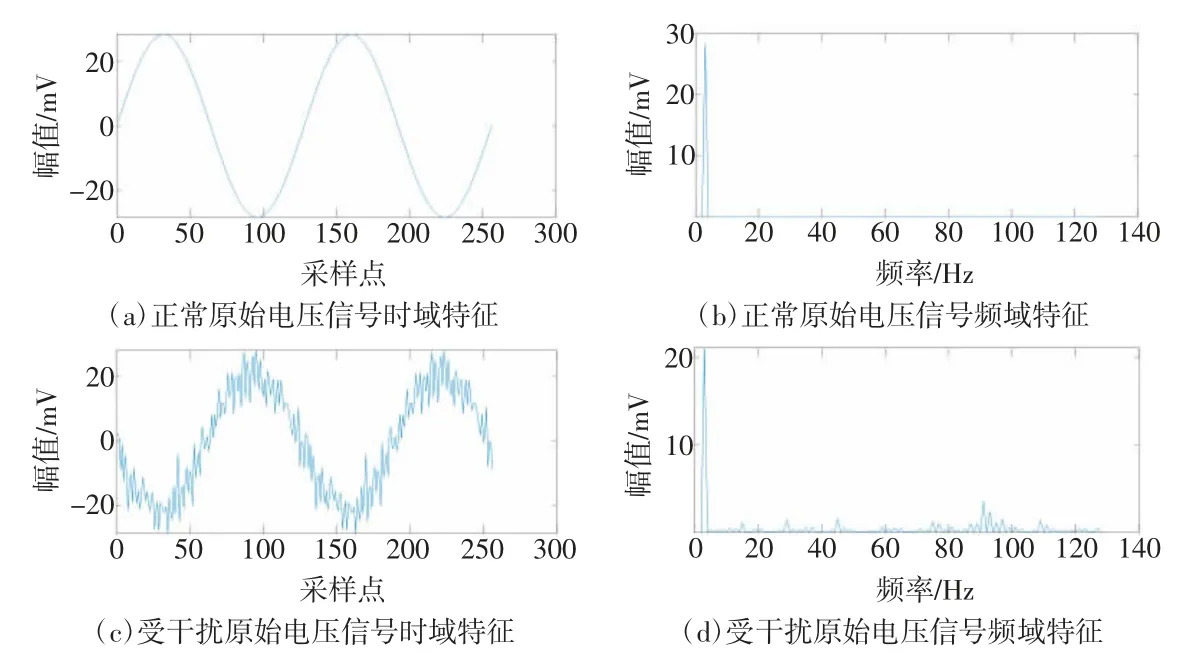
图6 正常与受体动干扰的原始电压信号时、频域结果

（2）小波包分解消除体动干扰。

使用小波包分解方法对志愿者试验中判定为受体动干扰的原始电压信号进行处理。从存在干扰的数据帧中任意选择4组（分为A、B、C、D组）受干扰原始电压信号，对比其处理前、后的时域结果图如图7所示，其相关系数以及解调值差分百分比结果详见表3。从表3中可以看出，小波包分解和重建方法使得原始电压信号与标准正弦信号的相关系数得到提升，更接近预设的阈值fth。同时解调值差分百分比的绝对值较处理前大幅度降低，即受干扰原始电压信号的幅值更接近于前景帧原始电压信号的幅值，而这有效地抑制了等效时间采样电压信号中的体动干扰。

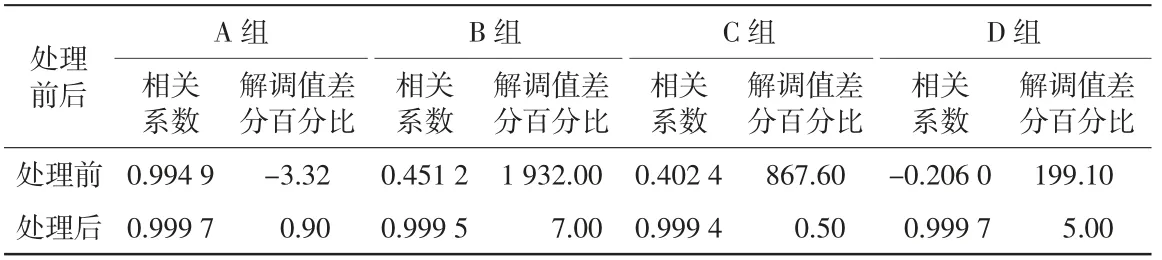
表3 4组受干扰原始电压信号处理前后的相关系数以及解调值差分百分比结果

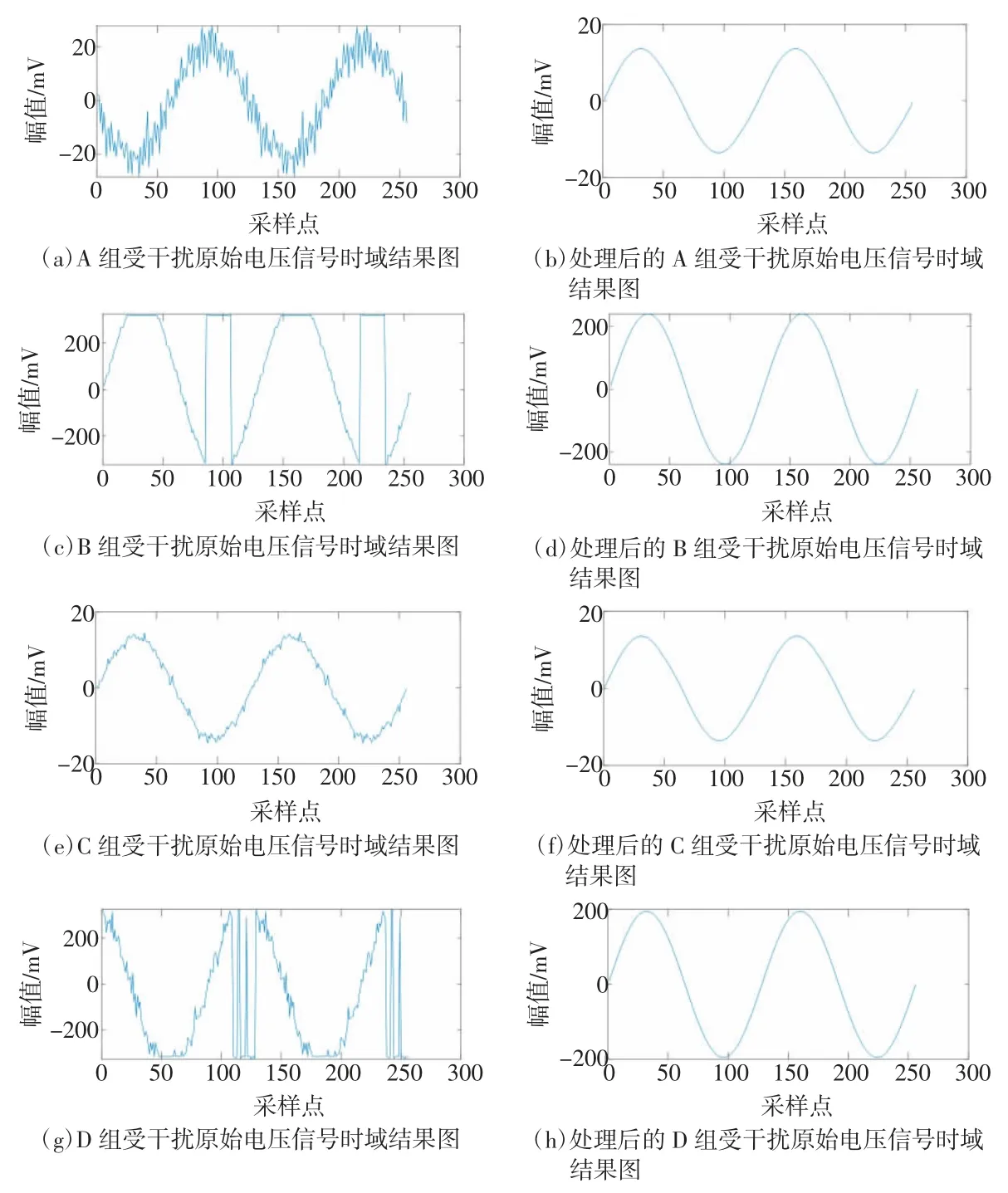
图7 4组受干扰原始电压信号处理前后的时域结果

将所有相关系数低于阈值fth的采集数据进行小波包分解处理后，原始电压信号的相关系数分布得到明显改善，详见表4。对于正常数据来说，相关系数大于fth（0.996）的占比由60.68%提高到72.00%，0.950~0.996的占比由14.32%降低到3.00%。受体动干扰数据的相关系数则全部≥0.950，其中＞0.996的占比由18.75%提高到24.61%，仅有0.39%处于0.950~0.996范围。本研究中的小波包分解方法能有效改善颅脑EIT原始电压测量数据的质量，尤其是能抑制体动干扰对测量数据的影响。

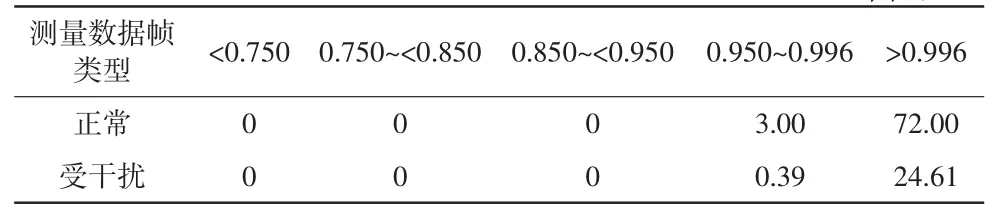
表4 处理后原始电压信号相关系数的分布统计单位：%

将处理之后的数据进行正交序列解调处理，并通过EIT阻尼最小二乘成像算法进行图像重构，结果如图8所示。对比处理前的成像结果（如图4所示），可以明显地看出体动干扰在EIT图像中产生的伪影得到了有效抑制。

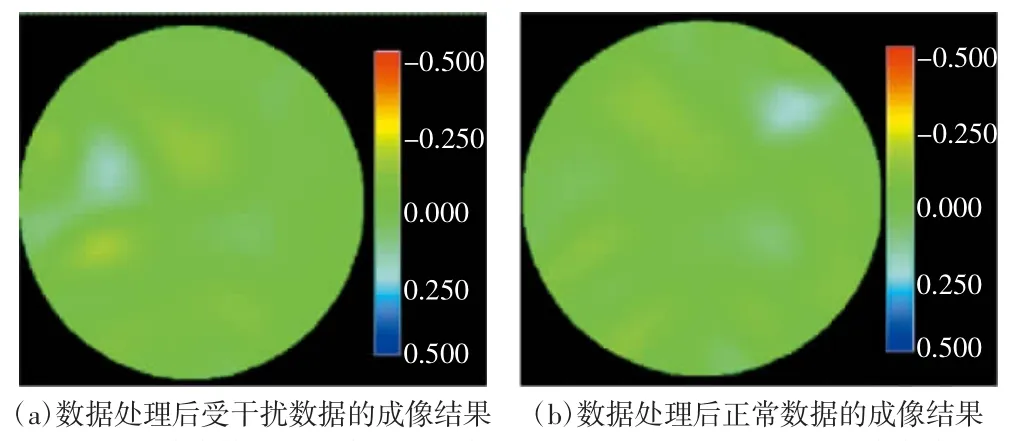
图8 处理后的重构图像

4 结语

本研究针对颅脑EIT临床使用中存在的采集数据受体动干扰问题，通过分析正常与受体动干扰的原始电压测量数据的差异，提出使用皮尔逊相关系数判断受干扰数据的方法，并基于小波包分解与重建方法实现对体动所产生测量数据偏置性干扰的抑制作用。志愿者监测试验结果表明，本研究所提方法能够有效地修正EIT原始电压信号等效时间采样中存在的体动干扰，改善采样信号的频谱质量，提高EIT效果。由于临床护理操作和患者体动会使EIT图像产生严重伪影，影响了颅脑EIT对患者病情变化的实时监测，因此消除和抑制体动干扰、提升信号采样精准度对颅脑EIT的临床应用具有重要意义。此外，EIT电极和皮肤接触阻抗的变化是导致测量数据体动干扰的根本原因，而本研究所提方法并不能评估EIT电极与皮肤接触阻抗的变化量，因此下一步将结合电极-皮肤接触阻抗的测量方法，进一步优化EIT原始测量信号干扰的识别与抑制方法。