基于多目标优化的风储协同一次调频控制策略
2022-12-01赵熙临李品付波
赵熙临,李品,付波
(湖北工业大学电气与电子工程学院,武汉430068)
0 引言
社会发展对能源需求的提升给能源供给带来了压力。为减少化石能源消耗,以风电、光伏为代表的新能源得到了广泛使用[1 - 2]。然而,风电等新能源的大规模并网会对原有系统的频率稳定控制造成冲击[3 - 4]。为了保证电力系统安全运行,在含风电的电力系统中,风电机组具备调频能力是必要的。
有关风电机组参与电网调频的研究主要有虚拟惯性和备用容量控制[5]。虚拟惯性控制以电网频率变化率为参考,通过释放风机转子动能来改变其有功输出进行电网频率调节,能够在系统频率发生变化时快速做出响应[6 - 7]。但是虚拟惯性控制对转子转速有约束,所能提供的有用功率增量有限。同时,在转子完成惯性响应后的转速恢复阶段,需要吸收或者释放额外的能量,从而导致系统的频率发生二次变化,故该控制方式需要限制机组的惯性响应时间或者研究额外的补偿措施[8]。
在备用容量控制方式中,研究较多的是桨距角控制[9 - 10]。该控制方式通过改变桨距角的大小使风机吸收的机械功率增大或者减小,调节范围较广,若通过风速分区确定运行状态,基本可实现全风速段的控制[11]。但该方法一方面存在弃风的现象,影响风电运行经济性;另一方面,由于执行机构涉及机械部件,响应速度较慢,不能很好地适应当前电网频率的快速调整需求,且桨距角的调整会造成机械磨损,频繁参与调频会进一步增加其维护成本[12 - 13]。因此,综合风电机组本身运行过程中存在的约束及风电的不确定性,需要有其他手段对含风电电力系统调频过程中风机的参与行为进行支撑。而储能电池由于响应速度快和输入输出可控性高等特征,可辅助电网调频,被认为是保障大规模风电并网后电网频率稳定的重要举措[14 - 15]。
储能参与电力系统调频主要是通过电池充放电对系统出现负荷扰动时的功率缺额进行补充。目前的控制方式主要有虚拟惯性和虚拟下垂控制。虚拟惯性控制可以减缓频率变化率,抑制频率的变化速度,使频率的变化更平缓[16];虚拟下垂控制则主要针对频率偏差,降低一次调频的稳态误差[17]。在这两种基本方法基础上,为了更好地控制调频效果,有研究根据频率的动态变化,实时调整虚拟惯性和虚拟下垂的分配比例系数,实现两种控制方式的平滑切换,提高控制过程中频率的暂态响应表现[18]。考虑到电池充放电深度对电池的老化有着显著的影响,充放电深度过高会减少电池的循环使用寿命,文献[19]提出基于动态任务系数的储能辅助一次调频方法,用系统运行时的储能荷电状态SOC数值做反馈,对储能的输出做实时调整,实现了储能的自适应控制,提高调频效果的同时,也减小储能电池充放电深度,提高其循环寿命。上述研究虽表明储能参与电网调频是可行的,但在储能参与过程中,其输出特征与荷电状态、充放电深度等具有复杂的耦合关系,需要进一步深入探讨。
研究上述耦合关系的主要目的是在储能参与电网调频中兼顾调频效果与储能运行经济性。在风储有功出力调整的基础上,使二者协同将有助于该目标的达成[20]。在此方向的研究中,目前多集中于风储协同的逻辑组合,即惯性阶段主要由风机出力阻止频率跌落,随着惯性响应结束,风机提供的有功支撑作用减弱,此时引入储能采用下垂控制弥补风机后期调频出力不足的缺陷,以提升调频效果且降低调频成本[21]。但在电网实际调频过程中,风储间的协同方式应更具准确性及可量化的优化特征。
针对上述问题,本文提出一种基于多目标优化的风储协同参与电网一次调频控制方法,综合考虑调频效果、桨距角磨损带来的风电成本、储能循环使用寿命间的耦合关系,对风储参与度进行优化,以实现多个控制目标间的平衡。
1 风储协同一次调频模型构建
以风储协同辅助传统火电机组参与一次调频为研究目标,构建出风储火协同的负荷频率控制系统结构如图1所示。系统主要包括:火电机组、风电机组、储能电池及交流电网等效模型。
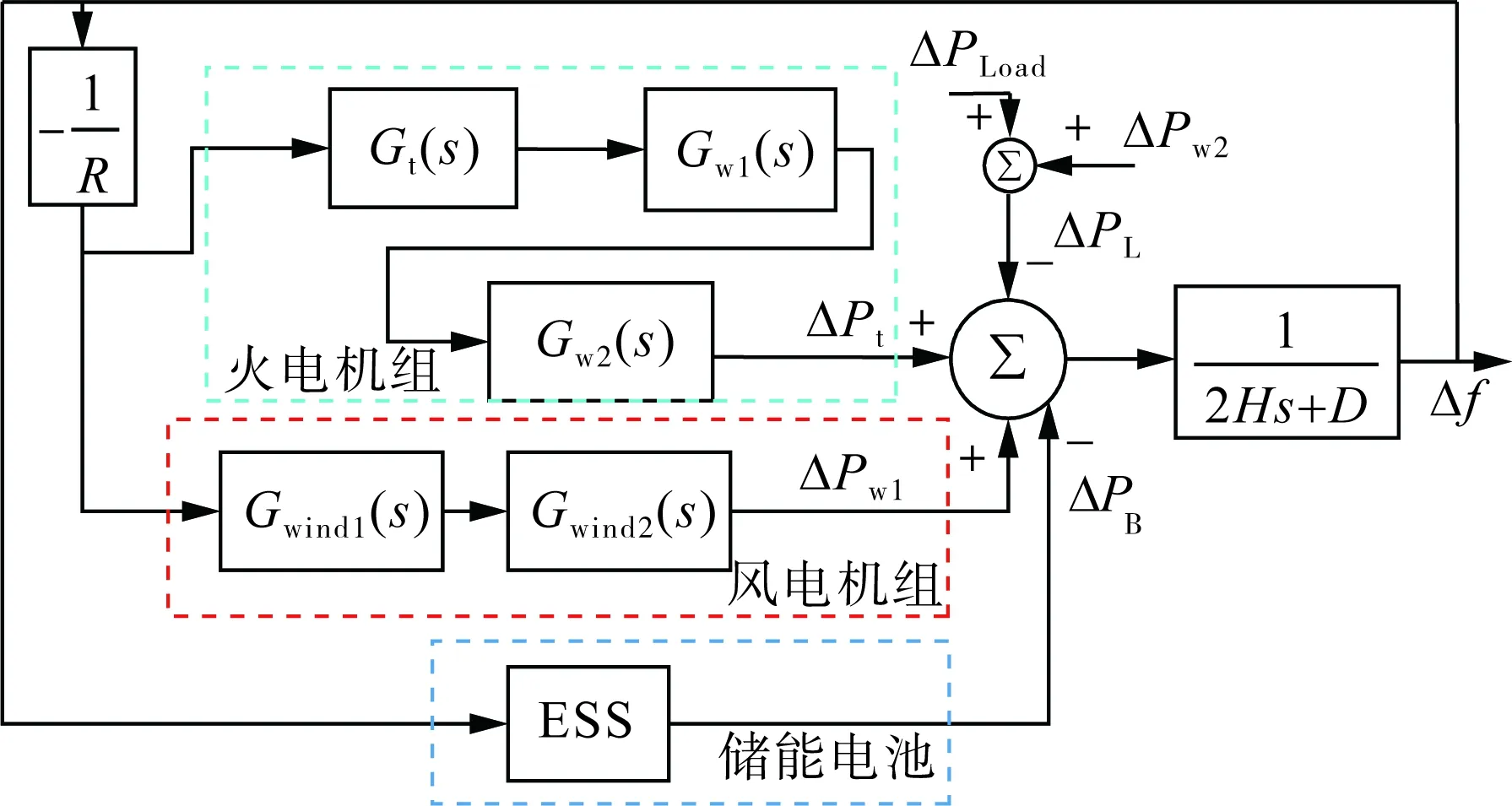
图1 风储协同负荷频率控制系统Fig.1 Wind-storage coordinated load frequency control system
火电机组主要由调速器以及再热式汽轮机构成。其中,调速器的传递函数Gt(s)为[22]:
(1)
再热式汽轮机的传递函数Gw被分为两部分:
(2)
式中:Tg为调速器时间常数;Tr为再热时间常数;Tt为气容时间常数;Kr为再热系数;s为拉普拉斯算子。
图1中其余各个变量的含义如表1所示。
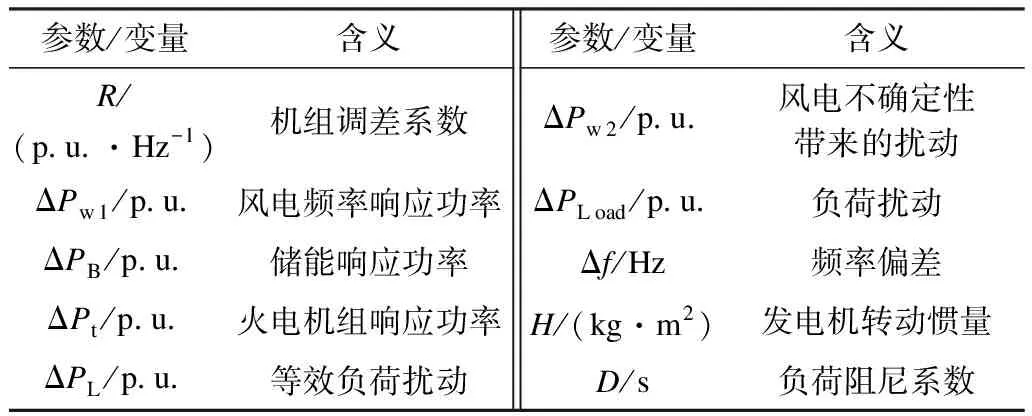
表1 电力系统参数或变量Tab.1 Parameters or variables of power system
2 风储输出控制方法设计
2.1 风电机组输出控制
由于风速具有不确定性,风电参与调频的有功出力变化需要能够适应风速波动。在风电参与调频的主要控制方式中,惯性控制下的风机有功输出幅值与时间尺度较小,并且与风速状态关联紧密,其控制过程不易与风速随机性解耦;而浆距角控制具有更大的输出调整范围及时间尺度,对风速的随机性更容易处理,因此,拟采用风机的液压变桨控制方法。
为了在风机变桨控制过程中使风机出力与风速随机性解耦,将风速V分解为一个恒定分量V′和一个变速分量V″, 即:
V=V′+V″
(3)
对应风速分解示意图如图2所示,其中,恒定分量V′对应恒风速,在变桨控制过程中,桨距角为满足调频需求进行的调整以该恒风速为基础,表现为恒风速下的变桨控制(V′的设定可视当地风速情况而定);而针对实际风速的随机性所分解出的变速分量V″, 在变桨控制过程中不做处理,其带来的风机随机输出等效为随机扰动,并与负荷扰动叠加。
风速分解处理后风电总输出分为2部分:参与调频的ΔPw1与等效为扰动的ΔPw2。如式(4)所示。
(4)
式中:ρ为空气密度;A为风轮机叶片扫风面积;Cp为风能转换系数;λ为叶尖转速比;β为桨距角;Ρ、A、λ、V′均为定值。故ΔPw1可以通过调整桨距角改变其大小,使风机具备可控的调频能力参与调频,ΔPw2等效为扰动。
为简化风机在风速恒定分量下利用桨距角控制参与调频的模型,可以用传递函数表示该控制环节,分两个部分,即液压变桨执行器和叶片特性[23]。
液压变桨执行器传递函数为:
(5)
式中:Tpw1和Tpw2为液压变桨执行器的时间常数;Kpw1为液压变桨执行器增益。
叶片特性传递函数如式(6)所示。
(6)
式中Kpw2为叶片特性增益。
得到的风电机组模型如图3所示。
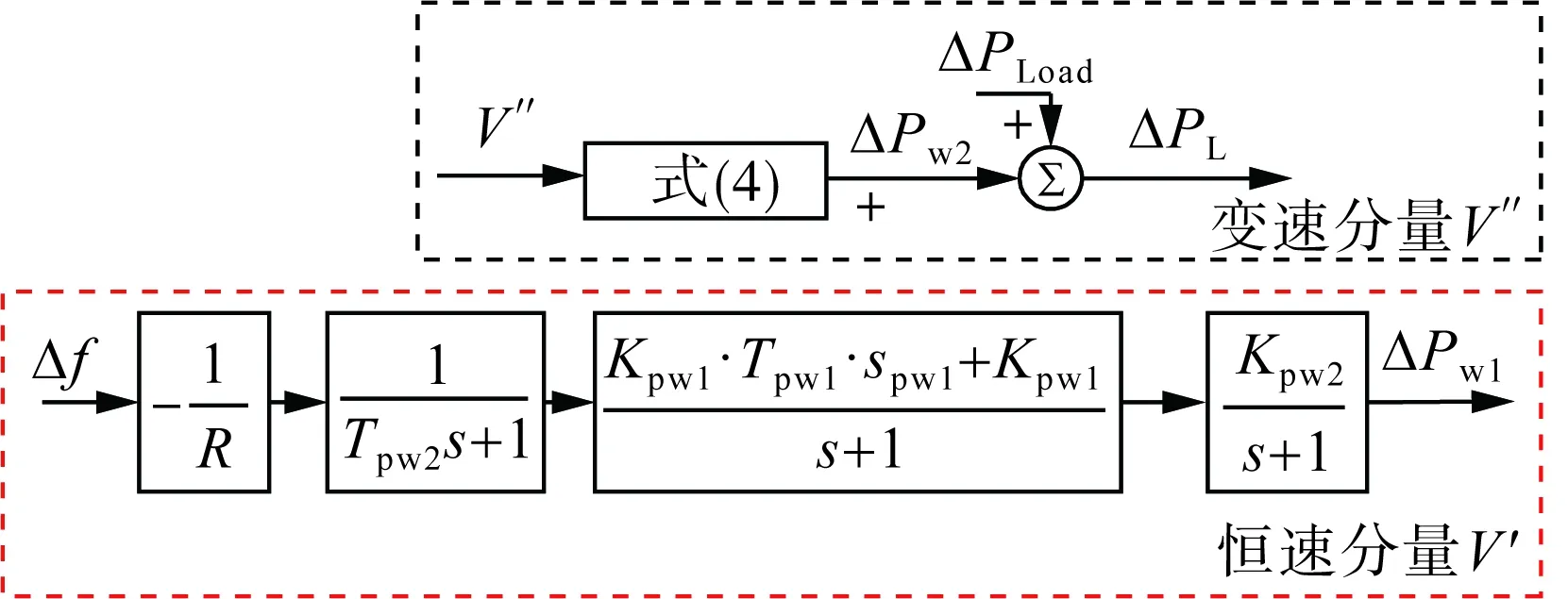
图3 风电机组模型Fig.3 Wind turbine model
2.2 储能电池输出控制
采用虚拟惯性和虚拟下垂相结合的综合控制方法,能够使储能出力较好地匹配电网调频的需求,其输出如式(7)所示[24]。
(7)
式中:ΔPB为储能响应功率;Δf为系统频率偏差;α1、α2分别为虚拟惯性模式和虚拟下垂模式下的分配比例系数;Me为储能电池的虚拟惯性系数;Ke为储能电池的虚拟下垂系数。
考虑储能输出控制的目标及约束,设计储能SOC自适应控制框图如图4所示。

图4 储能调频出力控制Fig.4 Energy storage frequency regulation output control
控制过程中,将储能SOC值(SSOC)设定4个临界点,分别为SSOCmin、SSOClow、SSOChigh、SSOCmax,据此将电池运行分为如下5个区域,如图5所示。
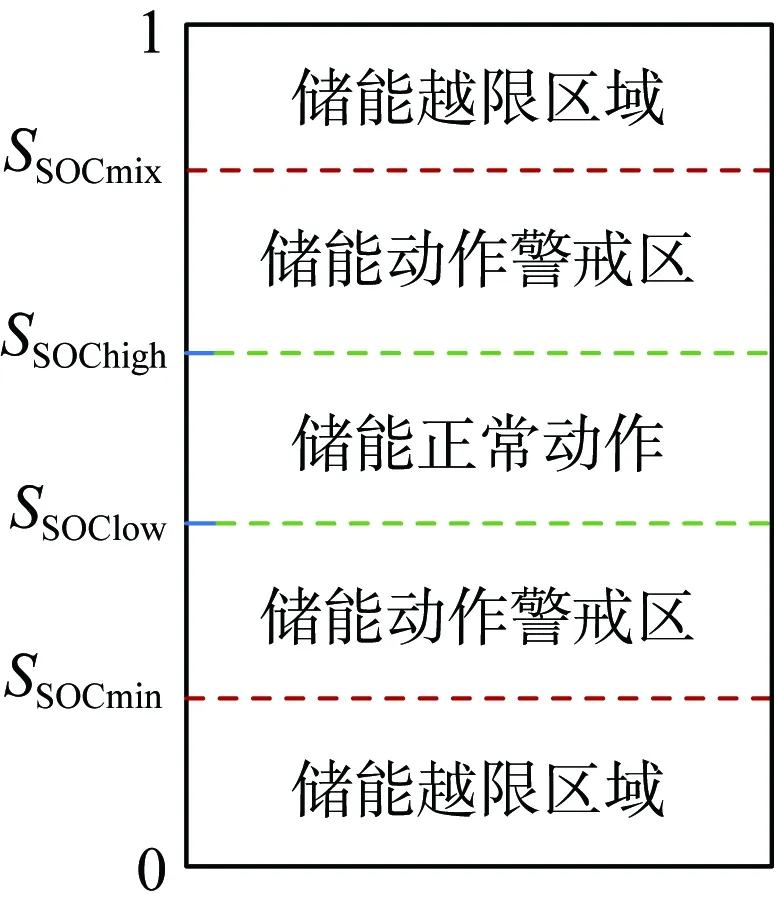
图5 SOC分区示意图Fig.5 Schematic diagram of SOC partition
SOC处于不同状态时,需根据充放电模式进行参数调整,形成储能充放电的自适应控制方式。
如电池放电时,当SOC值SSOC∈(SSOClow, 1],此时电池电量充足,以最大虚拟惯性和虚拟下垂控制系数进行放电,如式(8)所示。
(8)
当SSOC∈(SSOCmin,SSOClow]时,按式(9)进行参数调整以保证调频效果和电池SOC均衡。
(9)
当SSOC∈(0,SSOCmin]时,此时电池放电至极限状态,停止放电。即:
(10)
电池充电过程是上述的逆过程,在此不再赘述。
3 风储协同一次调频多目标优化问题设计
3.1 控制目标分析
在上述风储调频出力控制方法基础上,二者的协同需充分利用各自特点进行互补,达到电网调频综合效能最优的目标。
综合效能最优不仅体现在调频效果上,还应该考量调频代价。而根据所设计风储调频出力的控制方法可见,其出力越大,对应风储损耗越大,相应调频代价越高,但可得到更强的调频支撑。因此,要获得最佳的平衡,需通过多目标优化问题的设计与求解。式(5)中的Kpw1为液压变桨执行器增益,改变其数值等效为改变桨距角的调整量,从而影响风机一次调频的出力;式(7)中α1、α2分别为储能电池的虚拟惯性和虚拟下垂分配系数,Me,max、Ke,max分别为虚拟惯性和虚拟下垂系数最大值,4个参数进行调整可以改变储能电池的调频出力。故上述问题可转变为对这5个参数的优化求解问题,其求解结构如图6所示。

图6 风储协同优化结构框图Fig.6 Structure diagram of wind-storage synergistic optimization
3.2 多目标优化问题设计
根据上述问题,分别以调频效果好、风电成本低、储能循环寿命长为目标设计多目标优化问题。
1)调频效果
为合理地评估调频效果,将频率相对基准50 Hz的偏差量设计为频率控制目标函数一。即:
J1=|Δf∞|
(11)
式中Δf∞为稳态频率偏差。
2)风电成本
桨距角调整时会造成一定程度的机械磨损,且其磨损程度与风电调频出力正相关,故以风电机组调频输出功率的二次函数来评估风电机组的调频成本[22],设计目标函数二如式(12)所示。
(12)
式中r为风电机组功率偏移的成本系数。
3)储能循环寿命
电池储能的循环使用寿命与电池的使用环境及充放电深度有关,考虑到使用环境可控,在此仅讨论其与充放电深度之间的关联,关系式如式(13)所示[25]。
(13)
式中:NE为储能电池的循环寿命;HD为储能电池的放电深度,其范围为[0,1]。忽略电池初始状态的影响,则电池放电深度为:
HD=ΔSSOC
(14)
式中ΔSSOC为储能电池的SOC变化量,计算公式为:
(15)
式中:ΔPB为电池输出功率;PN为电池额定功率。
综合式(13)—(15),以电池的输出功率变化量来衡量电池的循环寿命,设计目标函数三为:
J3=|ΔPB|
(16)
同时,为了对多目标优化求解结果进行客观的综合评价,设定指标如下:
J=k1J1+k2J2+k3J3
(17)
式中k1、k2和k3分别为3个目标函数的权重系数,针对不同控制目标的需求可以有不同的权重系数配置。
3.3 约束条件
1)调频效果
按照国家标准,一次调频的稳态误差标幺值不超过0.004 p.u.。故调频效果约束为:
0≤|Δf∞|≤0.004
(18)
2)风电机组桨距角变化量约束
实际调频过程中风机桨距角变化一般在0~30 °之间,故液压变桨执行器增益Kpw1的约束为:
0≤Kpw1≤Kpw1,max
(19)
式中Kpw1,max为液压变桨执行器的最大增益,按照经验值一般取1.45。
3)储能电池约束
储能电池的约束主要有功率输出约束及荷电状态约束。针对功率输出约束,由于储能输出采用SOC自适应控制,其输出主要受α1、α2、Me,max、Ke,max4个参数影响,故转化为参数约束,如式(20)所示。
(20)
式中Me,max、Ke,max的最大值3.8和3.45为经验值。
针对其荷电状态约束,为了防止其出现过充或过放,对荷电状态进行限幅,即:
Ssoc,min≤Ssoc≤Ssoc,max
(21)
式中:Ssoc为电池SOC数值;Ssoc,min为SOC最小值,一般取0.2;Ssoc,max为SOC最大值,一般取0.8。
4 算法设计
考虑到本文多目标优化问题及对应约束条件关联性较强,为使优化出的结果不陷入局部最优与极端情况。因此,拟以遗传算法为基础进行问题求解,在传统遗传算法基础上,进行快速非支配排序,以便于优秀个体的保留,并且将原本为固定值的适应度偏差系数改为时变系数,使其可以在保证精确度的同时提高运行速度,算法步骤如下。
步骤一:初始化种群,当信号输入后,生成m组系统参数。
步骤二:将系统参数分别代入3个目标函数计算得到对应的适应度数值,保留适应度高的个体。
步骤三:系统参数进行交叉、变异。交叉采用模拟二进制算子计算方法,变异采用多项式变异算子计算方法。
步骤四:根据适应度值对系统参数非支配排序,并计算拥挤度,保留拥挤度较小的系统参数,使其在约束范围尽量均匀分布。拥挤度Id计算公式为:
(22)
式中:Δji为系统参数经过交叉变异变化后第i个目标函数的适应度变化量;ji,max、ji,min分别为第i个目标函数在当前系统参数组下的最大值、最小值。
步骤五:判断系统参数变化后的适应度变化量平均值M是否小于适应度偏差系数,如果是则停止运行输出结果,反之则继续完成后续步骤。计算及判断方法如式(23)所示。
(23)
式中:n为目标函数数量;δ为适应度偏差系数。
步骤六:对是否达到最大迭代次数进行判断,如果没有达到,就继续回到步骤二进行循环求解,直至迭代结束后输出最优系统参数解集、Pareto前端图以及对应系统稳定后的各个目标函数参考值。
对应求解流程图如图7所示,NGen为当前迭代次数,NmaxGen为最大迭代次数。
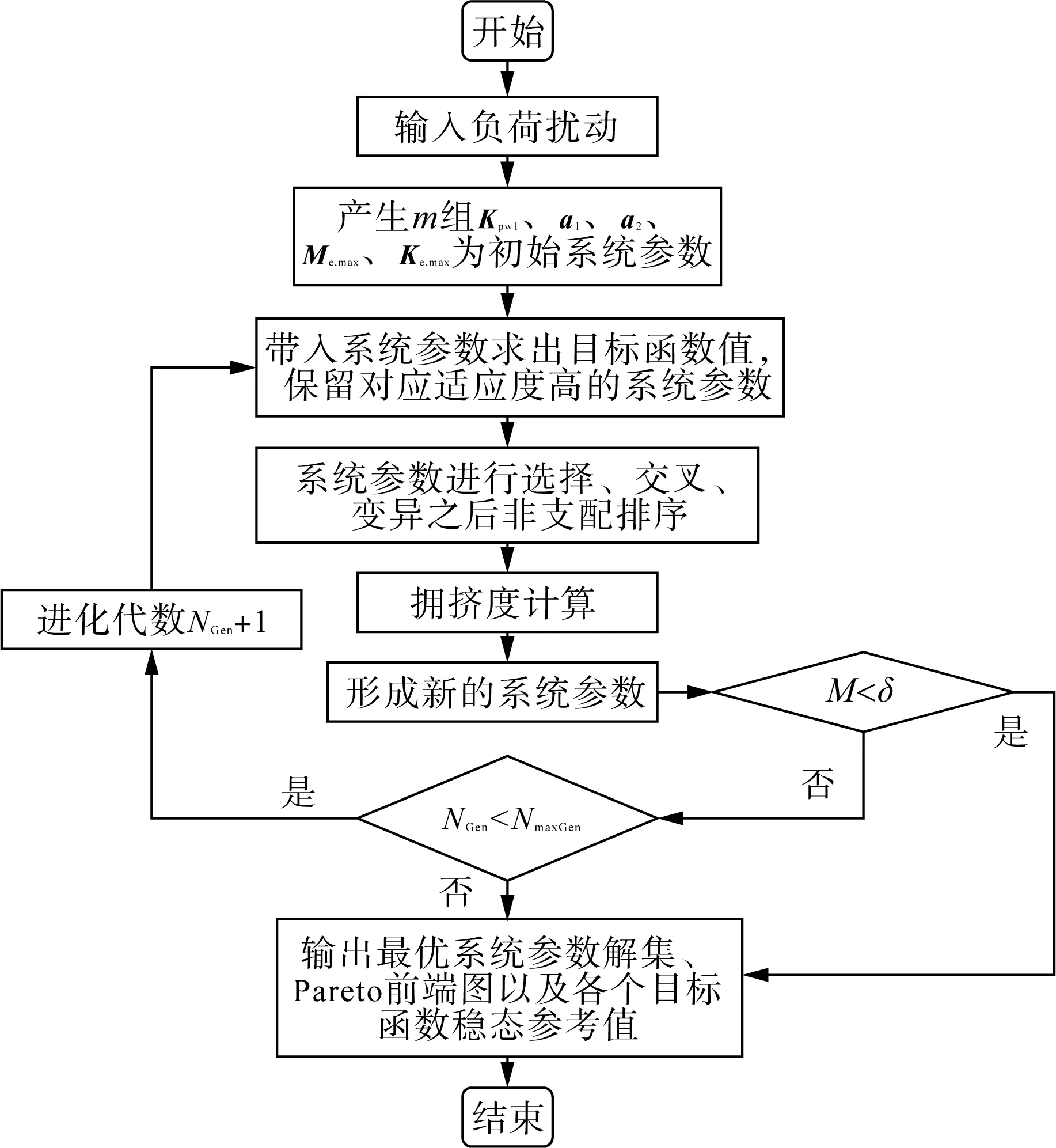
图7 算法求解流程图Fig.7 Solving process of the algorithm
5 仿真分析
5.1 仿真环境设置
为证明所提方法的可行性和有效性,在MATLAB/Simulink环境下进行仿真验证。使用图1所示的风储联合系统频率响应模型,其中包含一个容量为500 MW的火电厂,一个容量为150 MW的风电场(由100台1.5 MW的永磁直驱风电机组构成),一个容量为12 MW/3 MW·h的储能电池组,将初始SOC值设置为0.6,SSOCmin、SSOClow、SSOChigh、SSOCmax分别为0.1,0.45,0.55,0.9。系统采样周期T=0.03,对于算法中的参数设定,设定NmaxGen为300,m为200。其余各个仿真参数取值如表2所示。
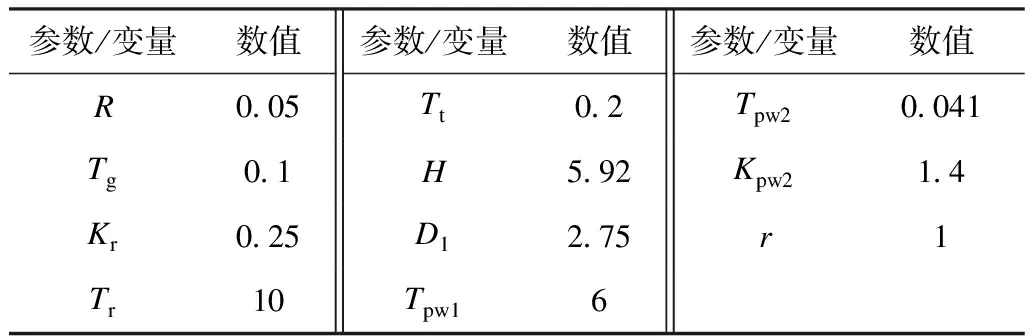
表2 电力系统仿真参数取值Tab.2 Power system simulation parameter value
5.2 阶跃扰动分析
设置t=10 s时有0.1 p.u.的阶跃负荷扰动,此时仅考虑恒风速下的调频问题,风机不会给系统带来额外干扰。运行算法,得到Pareto前端如图8所示。
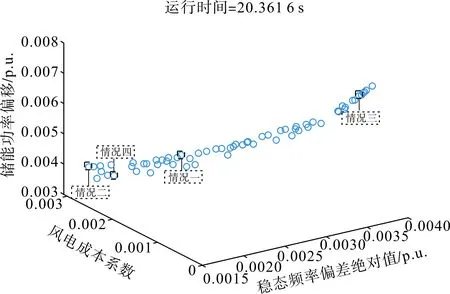
图8 Pareto前端Fig.8 Pareto frontend
算法求解后,根据3.2所述的最优解评价指标进行权重系数配置,选取综合指标最小的解作为最优解。本文中,假定情况一为三目标平衡,评价指标权重系数均取1;情况二为侧重调频的考量,评价指标系数k1取3,k2与k3取1;情况三为侧重风电成本的考量,k2取3,k1与k3取1;情况四为侧重储能循环寿命的考量,k3取3,k1与k2取1。考量重点对应权重系数取3是为了使其权重影响大于其余指标的综合影响。选出4个最优解对应的目标函数参考值及系统参数值分别如表3—4所示。
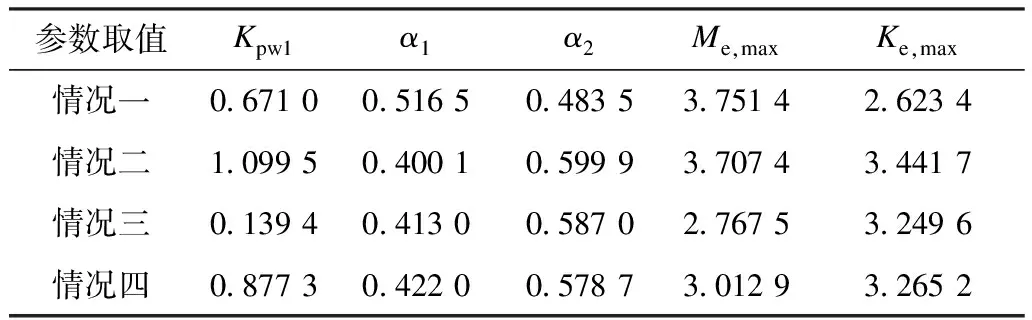
表4 系统参数值Tab.4 System parameter values
将上述选出的4组最优解对应的系统参数带入到仿真模型中,进行效果验证,系统运行后得到具体结果如图9—13所示。
从图9—13中可以看出,仿真结果和目标函数参考值趋势一致,为更具体化分析,将仿真得到的各个目标的具体数值导出如表5所示。可见,算法运行所得的目标函数参考值与仿真结果十分接近。

图9 频率偏差波形图Fig.9 Diagram of frequency deviation waveforms

图10 风电输出波形图Fig.10 Diagram of wind power output waveforms
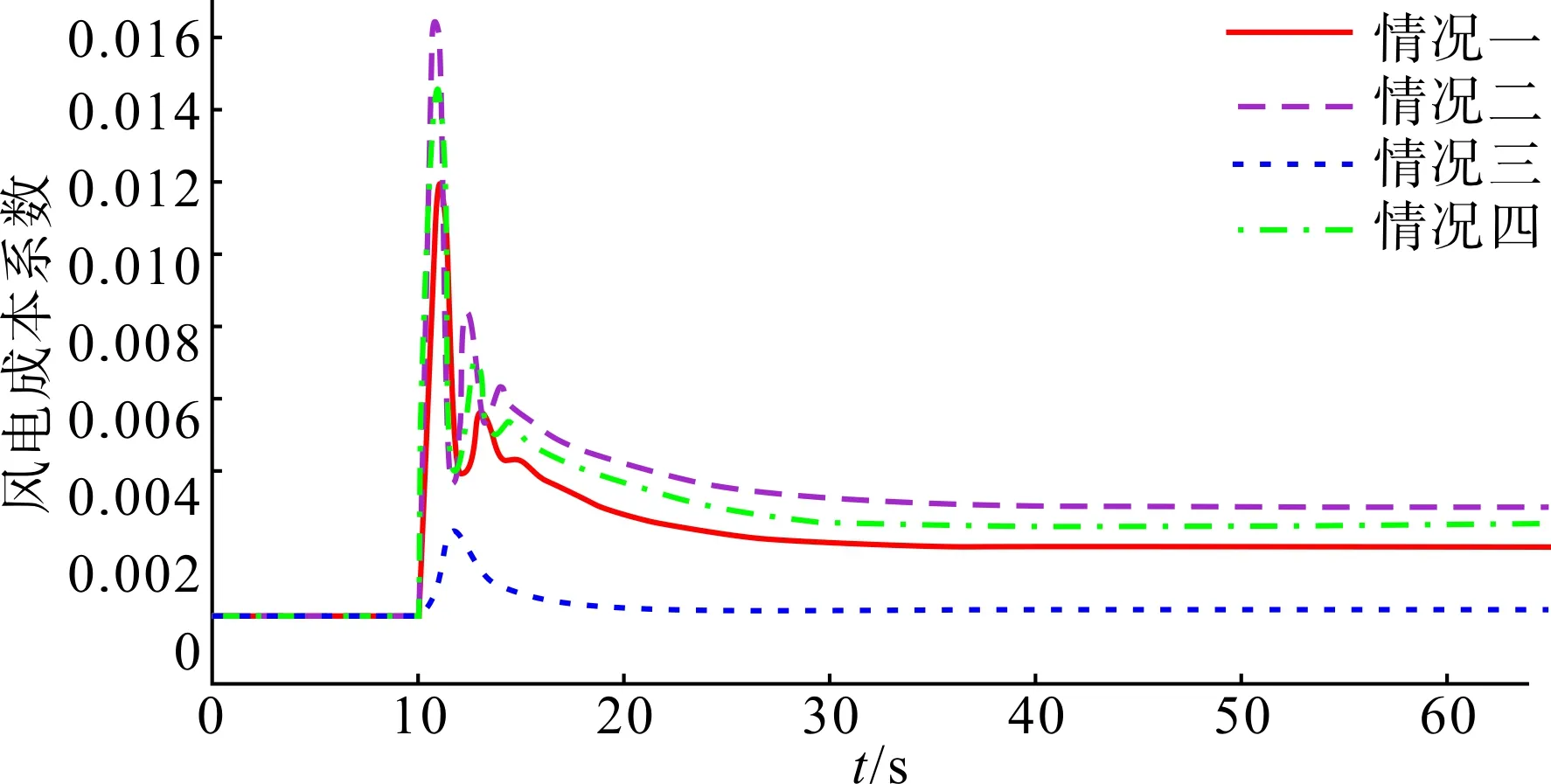
图11 风电成本波形图Fig.11 Diagram of wind power cost waveforms

图12 储能输出波形图Fig.12 Diagram of energy storage output waveforms
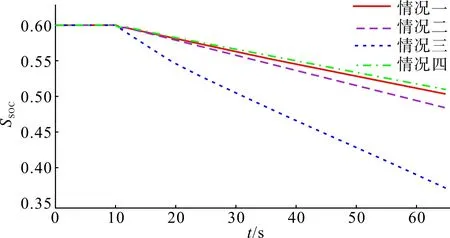
图13 SOC变化波形图Fig.13 Diagram of SOC changes
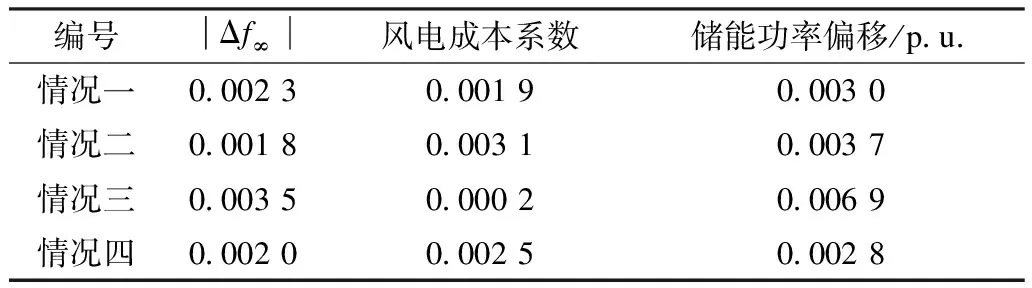
表5 仿真所得参数数值Tab.5 Parameter values obtained from the simulation
5.3 随机扰动分析
当风速不确定时,按照风速分解方法,不确定风速分量的风电输出视为扰动,其与负荷扰动叠加为等效负荷扰动,如图14所示。
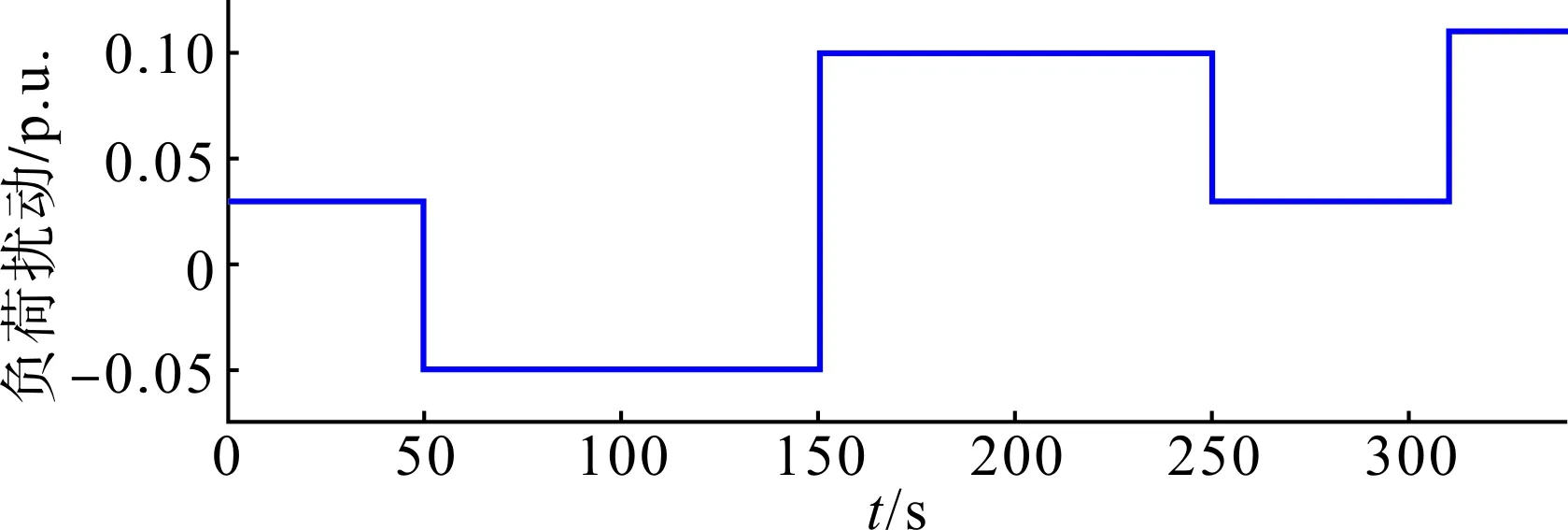
图14 等效负荷扰动Fig.14 Equivalent load disturbance
接入该等效负荷扰动后,仿真结果如图15—19所示。可见,随机扰动对应的控制特征与阶跃扰动具有一致性。同时,为满足调频的不同需求,可以根据制定的评价指标选取相应权重系数,以获取不同需求的最优解。
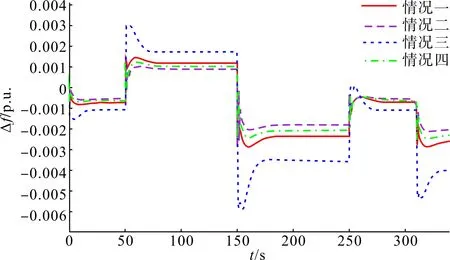
图15 频率偏差波形图Fig.15 Frequency deviation waveform diagram
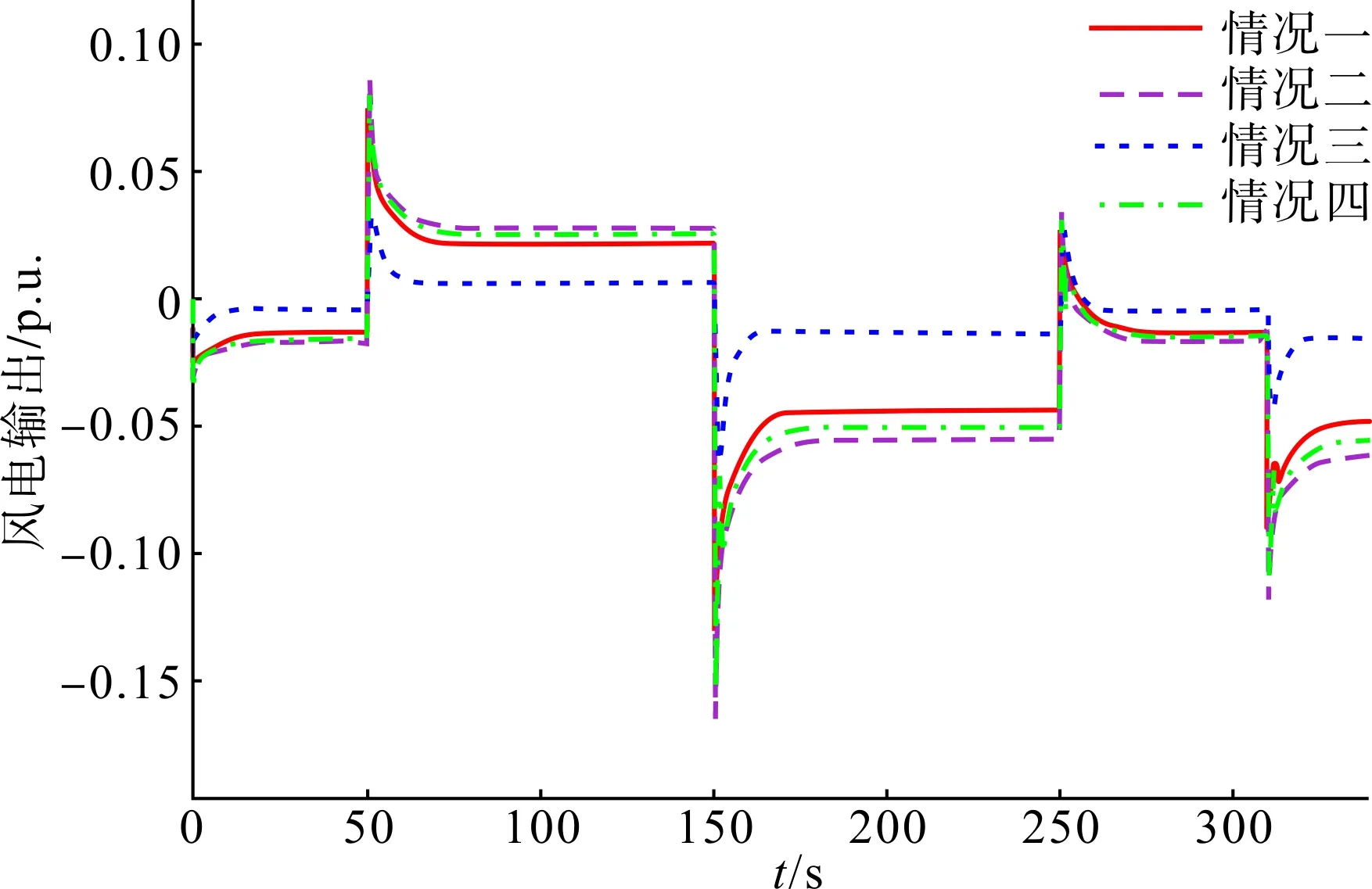
图16 风电输出波形图Fig.16 Wind power output waveform
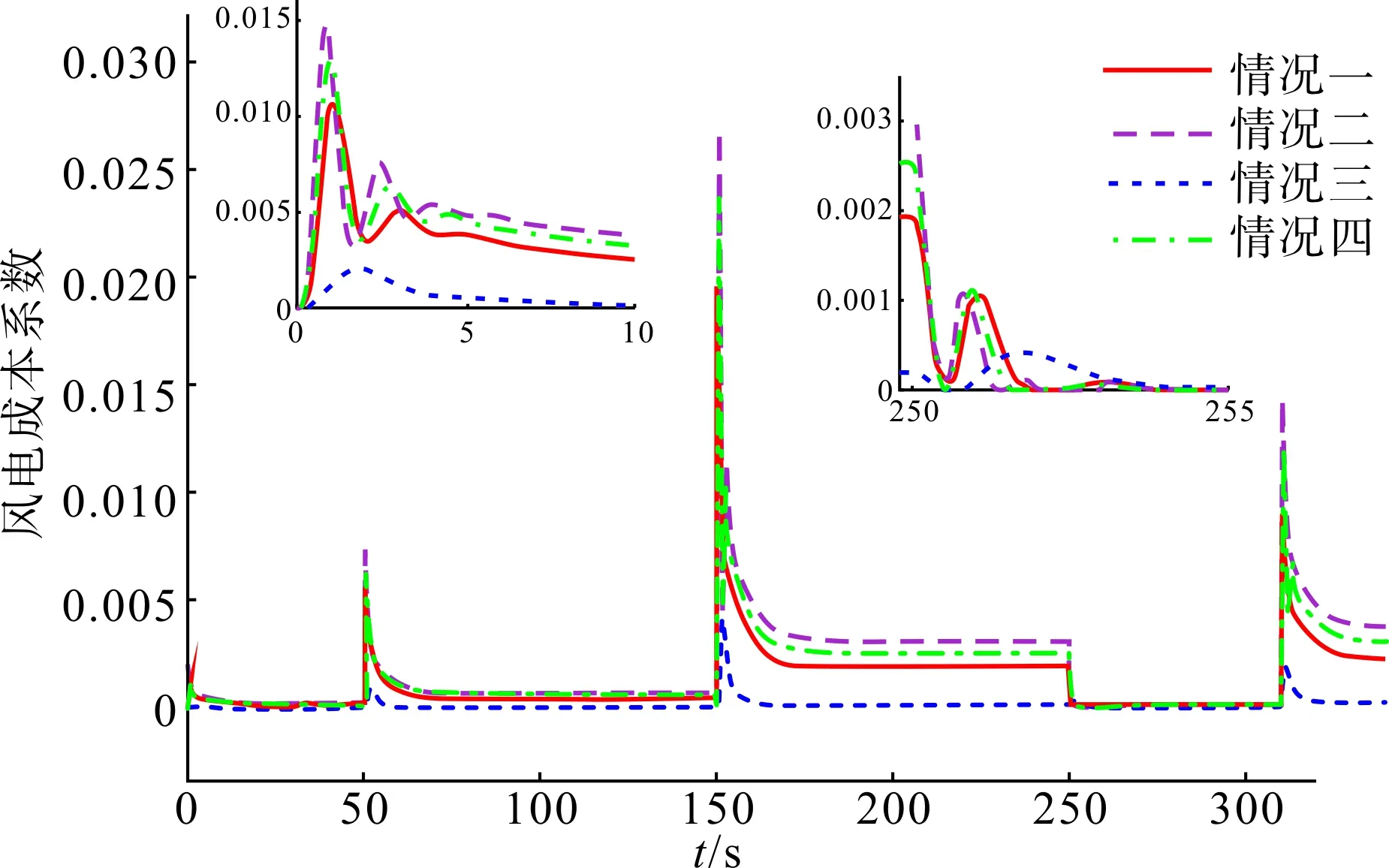
图17 风电成本波形图Fig.17 Wind power cost waveform
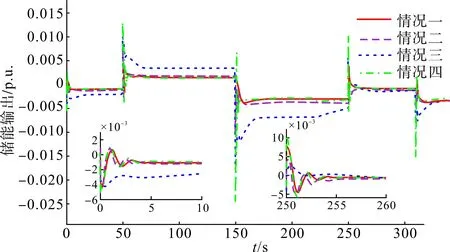
图18 储能输出波形图Fig.18 Energy storage output waveform
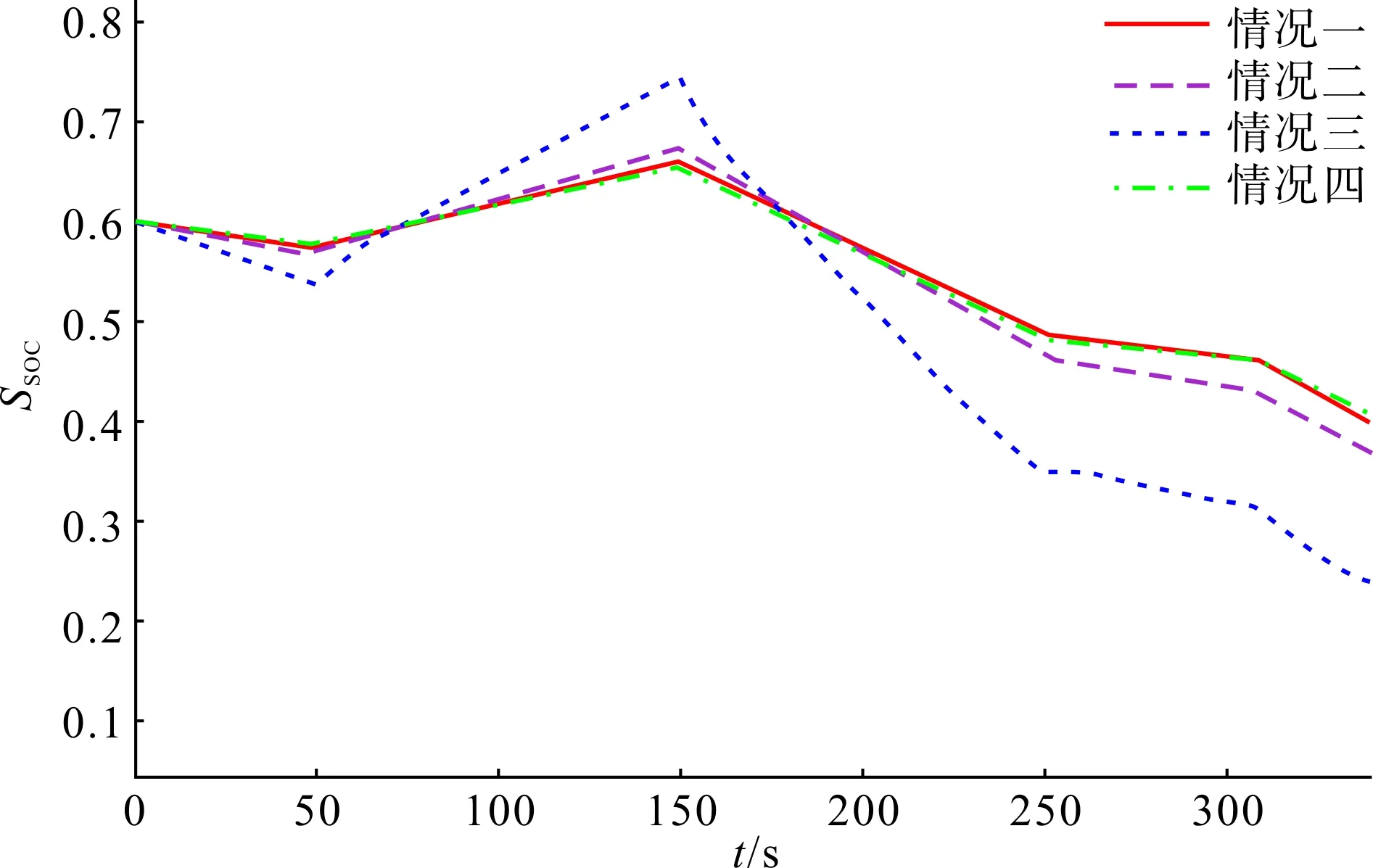
图19 SOC变化波形图Fig.19 SOC change waveform
6 结论
为了解决风储协同参与系统调频时,调频效果、风电成本以及储能充放电深度等多方面关联耦合对调频综合效能表现的影响,本文提出了一种多目标优化的风储协同一次调频控制策略。通过理论分析和仿真验证得出如下结论。
1) 对风机采用变桨控制,将其模型按风速进行分解,一部分为风速变化的随机性模型不参与调频,等效为系统扰动;一部分采用变桨控制的等效传递函数参与调频,能体现风速随机时风机的运行特征。
2) 对储能采用SOC自适应控制,使其调频出力随SOC变化而做出对应动态变化,可以有效降低储能充放电深度,延长储能循环寿命。
3) 以调频效果好,风电成本低,储能循环寿命长为目标设计多目标优化问题,可以反映风储调频需求与调频损耗之间的矛盾性。
4) 在多目标优化过程中,出于对不同调频需求的考量,可以在所设计的综合评价指标中通过相应权重系数的选择予以实现。
