井下巷道偏导支护方案设计及数值模拟分析

方珏静，杨 科，吕 鑫，3

（1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；2.合肥综合性国家科学中心能源研究院（安徽省能源实验室），安徽 合肥 230031；3.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室，安徽 淮南 232001）

随着我国煤炭资源逐步向深部开采，巷道变形失稳成为制约资源安全高效开采的1 个重要因素[1-2]。因此，研究巷道围岩控制机理，优化巷道围岩支护方式，提高支护效果，减小巷道变形失稳，降低支护成本，具有积极的理论和实践意义。文献［3-8］对开挖巷道顶板及承载结构进行受力分析，指出巷道以剪切变形破坏为主，拉伸破坏较少，且拉伸破坏主要集中在巷道浅部围岩；文献［9-10］基于巷道变形破坏理论，提出了顶板分区耦合支护和以充填区域顶板为关键纽带的“四位一体”围岩控制技术；文献［11-13］利用锚杆索进行支护，确定了打设在软岩巷道顶板和两帮处锚杆主要受轴向拉伸作用，而拱肩和底角处锚杆受到轴向拉伸与横向弯曲的综合作用；李建忠等[14]通过研究岩体抗拉强度、抗压强度等参数的变化来调整预紧力大小；谷拴成等[15]综合考虑围岩剪胀特性与中间主应力效应，建立了被锚巷道弹塑性力学模型；文献［16-19］认为浅部巷道变形量控制可以更换高强度支护材料或缩减间排距的方式达到，但深部巷道支护需要采取切顶及打设钻孔等方式进行卸压，为巷道转移围岩应力并提供补偿变形的能力；文献［20-22］指出遇多层开采或巷道交错情况时需使用错层位及远距离煤层布置方式进行卸压。综上，现有的支护研究主要集中于巷道迎头断面，对巷道走向方向的探讨仅限于超前支护方便巷道的掘进而忽略了走向支护对巷道围岩的控制作用。为此，通过理论分析巷道走向方向的应力传递机理，提出了偏导支护方案，利用FLAC3D建立数值模拟模型，对偏导支护的承载性能和支护成本进行研究。

1 围岩应力传导分析

井下巷道深部围岩应力难以准确测量，也无法实时记录其变化，因此通常使用巷道中的位移变化及浅部钻孔应力传感器得到的数据进行深部应力的反向监测，故可将应力传递（着重介绍顶板方向）分为3 个阶段：①深部围岩应力传递：除岩层中含大孔洞及侵入岩的情况外，此阶段的应力传递皆为均匀竖直传递；②顶板应力传递：此阶段应力传递受支护方式及巷道设计形状影响，应力方向会随之发生改变，但总应力大小始终守恒；③巷道应力传递：此阶段的应力受人工监测，并在巷道变形方面得以显现，通过监测顶底板及两帮支护材料上的应力及位移量大小，判断出支护方式及巷道形状对应力传递过程中的优劣性影响，分析受力结构，优化支护方案，此阶段数据是巷道围岩控制的最终体现，也是1种支护方式是否有效的判定依据。不同巷道形状应力传递如图1。

图1 不同巷道形状应力传递Fig.1 Stress transmission for different roadway shapes

由图1 可以看出：无支护的矩形巷道在整体围岩应力传递过程中并不能起到有效的阻碍或偏导作用，顶板围岩应力的施加依旧沿竖直方向对巷道产生作用；拱形巷道顶部则可有效的影响顶板应力传递过程，在顶板应力传递阶段中，上覆岩层压力均匀且竖直的分布在拱形周围，但进入下一步巷道应力传递后有明显的应力偏导效果，削弱了应力对巷道顶板岩层的作用而将大部分压力偏导至两侧煤柱，利用煤柱承载分担应力，达到控制巷道变形的目的。

从单一巷道断面角度分析，巷道的选择形状很大程度上可以分散应力对顶板的作用，从而控制围岩的变形。但从巷道走向角度分析，无论那个角度剖开，走向方向上的巷道均呈矩形向前推进，并且缺少煤层的支撑后巷道变形情况进一步加剧，区域内巷道甚至会出现整体下沉趋势。不支护条件的巷道应力传递如图2。

图2 不支护条件下的巷道应力传递Fig.2 Stress transfer of roadway without different support conditions

为应对此种情况，使用锚杆索对其支护，利用上覆岩层中的关键层对顶板进行悬吊以控制变形，但此方法仅能减弱下沉量并不能够改变巷道顶板的整体下沉趋势，在此基础上为了控制变形，利用钢棚支护方式，模拟煤柱（岩柱）进行区段化承载，使得巷道顶板变形量降低，顶板整体呈“凹”型变形，两侧钢棚受力承载限制顶板下沉，传统支护条件下的巷道应力传递如图3。此种支护方式被广泛应用，但仍存在缺陷，在遇软弱顶板区域时，岩层黏结性差、中部变形加剧易发生折断，故需要将钢棚不断加密，增加成本且影响巷道了正常使用，此外施工至断层或顶板垮落步距时，简单的钢棚支护不足以应对突发状况的发生，会迅速塌陷，带来不必要的井下安全隐患及经济损失。

图3 传统支护条件下的巷道应力传递Fig.3 Stress transfer of roadway in traditional support condition

结合上述巷道断面及走向方向的剖面图，提出1 种在巷道走向方向合理运用应力偏导手段的支护方式，偏导支护条件下的巷道应力传递如图4，在顶板中打设倾斜长锚杆，模拟拱形巷道时的应力分散作用，将顶板上覆岩层应力偏导至两侧钢棚上，充分利用钢棚自身承载能力，起到围岩控制的作用，并且在遇断层时，倾斜长锚杆可以有效发挥悬吊作用，避免中部顶板的突然垮落，为突发状况加强支护提供了缓冲时间，降低钢棚架设密度，减小了成本预算。

图4 偏导支护条件下的巷道应力传递Fig.4 Stress transfer roadway under partial support condition

2 巷道走向顶板受力分析

2.1 传统支护条件受力分析

为分析巷道顶板岩层变形，将巷道顶板受力简化为简支梁模型[8]，将两侧的钢棚简化为简支梁的两支座，简支梁受力分析如图5。设梁厚度为h，跨度为2a，顶板压力为Q，梁上部受均布荷载q=Q/2a，为了便于分析按照平面应变问题进行处理。

图5 简支梁受力分析Fig.5 Simply supported beam stress analysis

由简支梁平衡条件可计算出距左侧钢棚支点O点x 距离的横截面上剪力Fs（x）和弯矩M（x）为：

从图5 可以看出，顶板在弯矩M（x）作用下发生下沉，由静力平衡关系可得支梁横截面所受弯曲正应力σ 为：

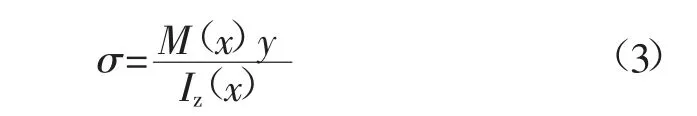
式中：y 为简支梁横截面上任意点到中性层的距离；Iz（x）为简支梁横截面对中性轴的惯性矩。

由图5 知，最大弯矩位于顶板中心位置，即在x=a 处存在顶板最大弯矩，为Qa/4；顶板与两侧钢棚连接处存在最大剪力，即在x=0 和x=2a 的处剪力达到最大，为Q/2。简支梁横截面上的最大弯曲正应力存在于距中性层最远处，即y=±h/2 处的弯曲正应力σmax最大，为σmax=3aQ/2h2。

从上述分析可知，在巷道走向方向顶板与两侧钢棚连接处位置剪力达到最大Q/2，此处顶板易剪切破坏；而顶板中部，弯曲正应力达到最大σmax=3aQ/2h2，易在此处发生拉断破坏。

2.2 偏导支护条件受力分析

同样将偏导支护条件下的顶板简化为简支梁模型，先假设倾斜长锚杆能够将巷道顶板处1/2 压力进行偏导，则顶板压力为Q/2，梁上部受均布荷载q=Q/4a，除此之外顶板的受力趋势基本与传统支护条件下相同。

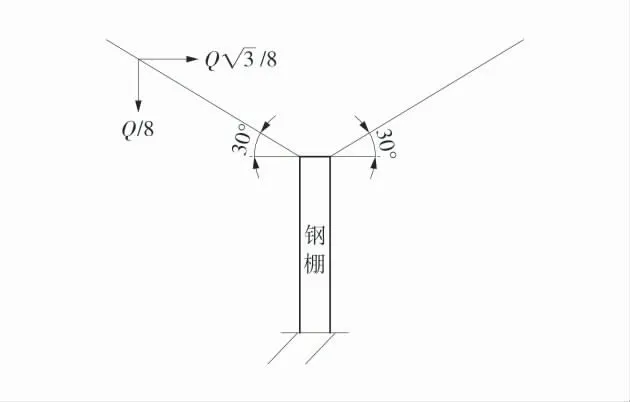
图6 钢棚承载受力Fig.6 Steel shed bearing force

3 不同支护方式数值模拟分析

3.1 计算模型及支护方案

选用有限差分软件FLAC3D设计相同巷道围岩岩性，岩层基本参数见表1，在同等埋深条件下巷道内进行数值模拟研究，对比巷道开挖后在无支护条件、传统支护条件及偏导支护条件下的变形、受力情况，通过对比分析验证偏导支护方案的合理性及偏导支护的优越性。

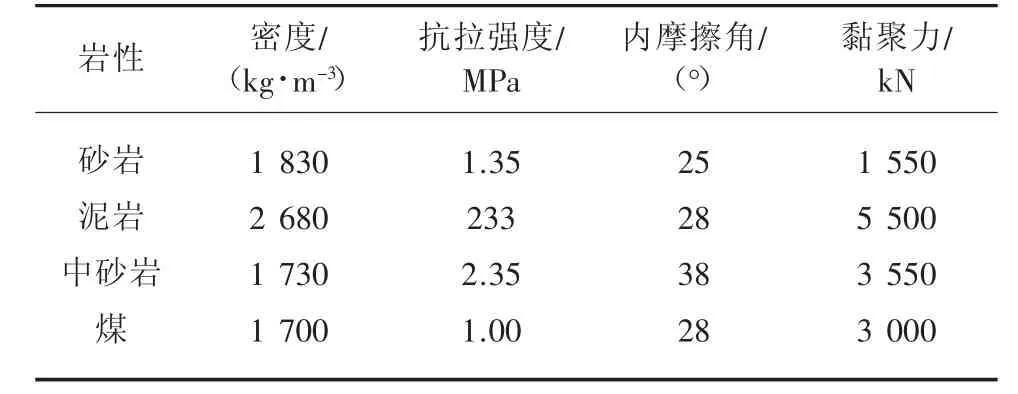
表1 岩层基本参数Table 1 Basic parameters of rock formation

采用CAD 绘制平面图并使用Ansys 进行三维拉伸机网格划分建模，导入FLAC3D软件中生成x 方向80 m、z 方向60 m、y 方向10 m 的数值模型，，模拟280 m 埋深下，高×宽=3 m×4 m 的矩形巷道在不同支护条件下围岩应力分布及巷道变形情况。

限制数值计算模型的边界条件为四边及底部固定，模型顶部为自由边界以施压应力，初始模型进行运算在应力平衡后再调用后续命令进行巷道开挖并及时进行不同方式的支护。传统支护方案设计如图7，传统-偏导支护方案设计如图8，优化-偏导支护方案设计如图9。

图7 传统支护方案设计Fig.7 Traditional support scheme design

图8 传统-偏导支护方案设计Fig.8 Traditional-partial guide support scheme design

图9 优化-偏导支护方案设计Fig.9 Optimization-partial guide support scheme design

1）传统支护方式。设计为工字钢棚架设间排距1 000 mm[23]，锚杆打设在2 排工字钢中间，左右两帮各打设2 排锚杆，顶板打设3 排锚杆，排间距1 000 mm×1 000 mm，为达到对照分析作用，锚杆统一长度为2 000 mm。

2）传统-偏导支护方式。在原有支护方式锚杆及钢棚的基础上打设倾斜长锚杆，间排距为2 m，即每隔1 架工字钢进行打设，且呈五花布置，在顶板内形成2 m 宽，4 m 高的等腰交错三角形。

3）优化-偏导支护方式。每隔1 m 减装1 架工字钢棚，即减少1/3 的工字钢棚使用，同时打设顶部倾斜长锚杆，在原中央钢棚顶板上方4 m 处相错交汇, 同样形成2 m 宽，4 m 高的等腰交错三角形。

数值模拟目的为验证不同支护方式及支护原理的区别而非支护材料的不同，故在模拟过程中巷道支护采用的锚杆及工字钢棚皆采用统一的支护参数，支护材料参数如下：①锚杆：预应力60 kN，弹性模量90 GPa，抗拉强度310 MPa，水泥浆黏聚力100 kN；②工字钢：弹性模量200 GPa，泊松比0.3，横截面70.65×10-3m2，密度7 800 kg/m3。

3.2 数值模拟垂直位移结果

对比不同支护条件模拟下垂直位移的分布情况，不同支护方式垂直位移图如图10，不同支护方式垂直位移表见表2。

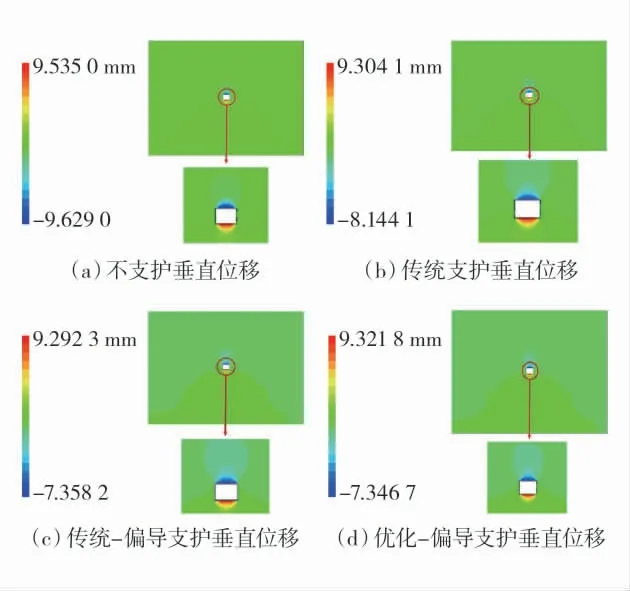
图10 不同支护方式垂直位移图Fig.10 Vertical displacement diagrams of different support methods

从图10 及表2 可以看出，不采用支护时，顶部及底部岩层变形量相差较小，而采取必要的支护手段后，顶板下沉量得到了明显的控制，说明支护手段可以切实有效的控制围岩变形，但由于采用的锚杆及钢棚皆侧重于顶板及两帮的支护，底板并未进行任何处理，因此对底部岩层变形影响较小。进一步更换为偏导支护方式后，顶部岩层的变形量明显下降，由传统支护的8.144 1 mm 降至7.358 2 mm与7.346 7 mm，降幅达到9.65%、9.79%。将顶部岩层变形与底部岩层变形数值之和视为岩层离层值，可以明显看出，使用传统支护手段能够大大降低岩层离层值，由原本不支护下的19.164 0 mm 降低至17.448 2 mm，降低8.95%，而使用传统偏导支护手段可以将岩层离层值降低至16.650 5 mm，降低13.12%，进一步优化后的偏导支护则将岩层离层值降至16.668 5 mm，降低13.02%，可以证明，在使用偏导倾斜长锚杆后，巷道整体变形量能够得到非常有效的控制。

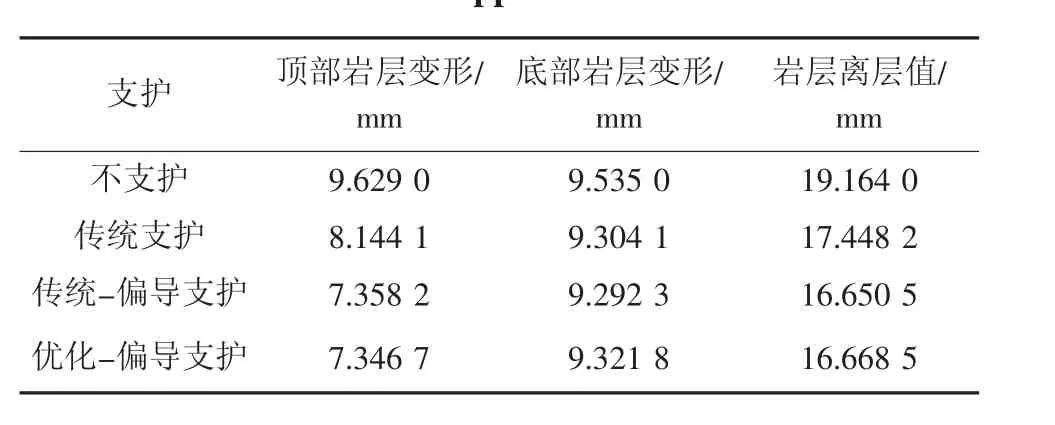
表2 不同支护方式垂直位移表Table 2 Vertical displacement table of different support methods

进一步在巷道顶板中心位置每隔1 m 布置1 个测点（即每架工字钢棚顶板位置），记录巷道走向方向上的垂直位移，编制成表，顶板中心点位移量见表3。

表3 顶板中心点位移量Table 3 Top plate center point displacement

由表3 可以清晰看出，在模拟过程中使用到的不同支护手段均能够阻止巷道顶板的变形，且使用传统支护方式将不支护时的9.625 1 mm 变形降低至7.929 4 mm，加倾斜长锚杆并再次优化后分别降至7.021 6 mm 与7.005 0 mm，分别降低了17.62%、27.05%与27.22%，偏导支护效果明显。

由于优化-偏导支护与其他2 种支护相比较在1、3、5 m 等位置减少了工字钢棚的安装，故挑选这些节点绘制曲线，顶板部分位置位移量如图11。

图11 顶板部分位置位移量Fig.11 Position displacement of the top plate

对比3 条曲线可以看出，位移量基本呈先下降后上升趋势。常规支护的位移量为7.900 7、7.897 7、7.908 9、7.955 5、7.998 8 mm 加设倾斜长锚杆后的位移 量为6.989 4、6.977 4、6.975 9、7.032 7、7.064 9 mm，分别降低了11.53%、11.65%、11.80%、11.60%、11.67%，平均降低了11.65%，而优化-偏导支护虽然减少了钢棚的架设，但在支护效果上却达到了更好的效果，位移量为6.969 9、6.963 1、6.960 7、7.020 2、7.044 9 mm，分别降低了11.78%、11.83%、11.99%、11.76%、11.93%，平均降低了11.86%，可以证明偏导倾斜长锚杆的使用可以有效降低中部顶板的位移量，并且其效果优于同等条件下加装工字钢棚，说明偏导倾斜长锚杆的使用完全可以替代工字钢棚，缩减支护工序同时降低成本仍保证良好的支护效果。

再对在巷道底板中心位置每隔1 m 布置1 个测点，记录巷道走向方向上的垂直位移，底板中心点位移量见表4，底板中心位移量如图12。

由图12 可以看出，3 种支护方式下的顶板位移量趋势相仿，3 条曲线呈现清晰的分层现象，其中传统-偏导支护方式最佳，传统支护方式次之，而优化-偏导支护效果差强人意；但结合表4 来看，3 种支护方式底板平均位移量依次为9.295 3、9.284 7、9.311 9 mm，相比于传统支护方式位移量，传统-偏导支护位移量降幅为0.11%，而优化-偏导支护位移量则增加了0.18%，说明了优化-偏导支护方式在底板位移控制上略有不足，但巷道整体变形量控制上仍具有优势。

表4 底板中心点位移量Table 4 Floor center point displacement

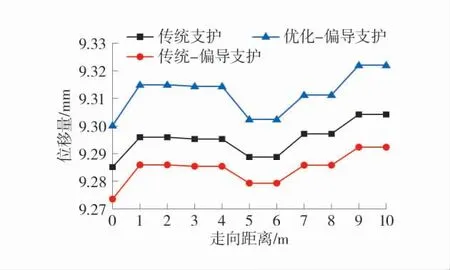
图12 底板中心位移量Fig.12 Bottom plate center displacement

3.3 数值模拟垂直应力结果

不同支护条件形式下的垂直应力模拟结果如图13，不同支护方式垂直应力见表5。

从图13 及表5 可看出，在巷道内使用支护手段后，在巷道周边围岩内形成局部的应力集中，应力值远大于不支护条件下应力自然平衡的巷道。在使用传统支护及偏导支护后巷道数值模拟中垂直应力分布相似，其中传统-偏导支护方式与传统支护方式相比，无论正向应力还是反向应力均有增加，增幅分别为2.88 %与0.43 %，不利于围岩的稳定，而优化-偏导支护后垂直应力得到较大程度降低，与传统支护相比，正向应力及负向应力降幅分别为2.06%与2.08 %，验证了偏导支护方式对巷道围岩控制的可能性。

表5 不同支护方式垂直应力表Table 5 Vertical support of different support methods

图13 不同支护方式垂直应力图Fig.13 Vertical stress diagrams of different support methods

3.4 数值模拟塑性区结果

不同支护条件塑性区如图14。

图14 不同支护条件塑性区Fig.14 Plastic zone with different support conditions

由图14 可以看出，采取支护手段后，巷道断面塑性区面积明显减小，而加设偏导倾斜长锚杆后塑性区进一步减小，同时从巷道断面图观察巷道两帮塑性区变化，在采用优化-偏导支护方式后，围岩破坏无法继续深入，仅限制在两帮浅部岩层中。

从巷道走向方向剖面图进行分析，不支护及传统支护中的顶板破坏受力复杂，受多方向上的剪切破坏，而加设倾斜长锚杆的巷道中，顶板中大部分破坏较为简单，仅为单一方向上的剪切破坏，二次补强及巷道的维护更加简单。

4 经济效益计算

支护方式中皆采用工字钢棚及锚杆支护，但不同在于偏导支护方式使用了倾斜长锚杆，将支护材料价格汇总编表，支护材料价格如下：①φ20 mm×2 000 mm 短锚杆单，单价42 元；②φ20 mm×3 700 mm 长锚杆，单价85 元；③11#工字钢棚，单价117 元。

为对比各种支护方式的造价成本，以巷道走向方向10 m 支护为例进行成本计算。传统支护方式共计需要短锚杆70 根，工字钢棚架设110 m，共计成本为15 810 元；传统-偏导支护方式共计需要短锚杆70 根，长锚杆25 根，工字钢棚架设110 m，共计成本为17 935 元；优化-偏导支护方式共计需要短锚杆70 根，长锚杆25 根，工字钢棚架设60 m，共计成本为12 085 元。与传统支护方式相比，优化-偏导支护方式成本节约23.56%，且在巷道变形与应力控制方面表现更为优秀。

5 结 语

1）传统锚杆-钢棚支护下的顶板与两侧钢棚角部位置易发生剪切破坏，而顶板中部易发生拉断破坏，基于传统支护条件加设偏导倾斜长锚杆可以有效发挥悬吊作用，避免中部顶板的突然垮落。

2）在同等埋深条件下进行巷道数值模拟研究，对比巷道开挖后无支护条件、传统支护条件及偏导支护条件下的变形、受力情况，可知偏导倾斜长锚杆的使用可以有效降低中部顶板的位移量，且其效果优于同等条件下加装工字钢棚，使用传统-偏导支护后顶板位移量较传统支护方式下降0.11%，优化-偏导支护可较大程度降低垂直应力，与传统支护相比正向应力及负向应力降幅分别为2.06%与2.08%，验证了偏导支护可有效减小巷道变形及应力集中。

3）优化-偏导支护在保证巷道变形及受力稳定的前提下，减少了45.45%的钢棚使用量，降低了23.56%的成本，并在巷道后期维护方面具有优势，一定程度上证明了偏导支护的可行性。