基于协同进化多目标遗传算法的复式液压摆动缸结构设计

2022-12-01李阁强董振乐

船舶力学 2022年11期

李阁强，袁畅，王帅，毛波，董振乐

（1.河南科技大学机电工程学院，河南洛阳 471003；2.河南省机械装备先进制造协同创新中心，河南洛阳 471003；3.山东万通液压股份有限公司，山东日照 262313；4.河南科技大学车辆与交通工程学院，河南洛阳 471003）

0 引言

舵机是舰船最重要的辅机之一，是操纵舰船航向、保障舰船安全和航行性能的关键设备。转叶舵机由于结构紧凑、安装简便、噪音小等优点，得到了广泛应用[1-2]。水动力作为一种干扰负载的存在严重影响舵角的控制精度[3]，本文设计出一种复式结构液压摆动缸，从结构上提出操舵原理，从根源上抵消水动力对舵驱动缸的耦合力矩。

复式液压摆动缸作为一种新型液压元件，缺乏理论支撑指导设计其尺寸参数，在常规液压缸设计时，通常都是对结构元件进行运动学或者动力学分析，对关键的部件进行强度校核[4]，此类方法只能求出关键部件的尺寸参数，对于求解整体结构的尺寸参数不具有适用性。对于数值优化方法[5-7]，如梯度法、序列二次规划、约束变尺度法等传统算法求解多变量、强非线性的优化结果一般都是局部最优，不能保证全局解最优。黄维等[8]和Wu 等[9]所使用的遗传算法，其优胜劣汰的思想原则十分契合结构优化设计，但是当目标函数和约束条件过多时，要考虑目标之间的冲突，单个目标所求的结果对其它目标来说通常是不可接受的。

基于此，本文首先建立以摆动缸壳体内径、力矩解耦缸转子内径、驱动缸转子轮毂直径、动静叶片高度、动静叶片宽度和壳体厚度为设计变量的优化模型，然后采用基于协同进化原理的遗传算法寻优。该算法包含两类种群，其中一类种群用于罚因子进化并指导另一类种群决策解的进化，把罚因子也作为寻优变量，在种群搜索过程中通过自适应地调整罚因子，指导式地更新种群状态从而提高全局搜索能力，得到最优解。与传统的遗传算法对比表明，其优越性在于其能确保各零部件在高压油的作用下仍能满足结构强度、刚度和安全系数要求，且尽可能地减小复式液压摆动缸的质量和体积，降低制造成本。

1 复式液压摆动缸结构设计模型及解耦原理

1.1 复式液压摆动缸解耦原理

如图1 所示，复式液压摆动缸作为一种新型执行元件，由驱动缸转子、力矩解耦缸转子、壳体、定叶片和动叶片等组成。驱动缸转子与解耦缸转子之间形成内密闭容腔，解耦缸转子与壳体之间形成外密闭容腔，内外层转子上均开设环形油道，内密闭容腔采用轴配流的方式配流，外密闭容腔采用壳体配流的方式配流。在高压油液进入内密闭容腔后，驱动缸转子在液压力F作用下顺时针转动，此时舵叶在与驱动缸转子固连舵杆的带动下顺时针旋转角度θ。在舵叶转动过程中必然存在反方向水动力F′的干扰，使容腔I 体积减小ΔV，转子到达新的平衡位置，对于传统摆动缸（单层摆动缸）转子将回旋，造成跑舵。而复式摆动缸为确保驱动缸转子不动，可通过顺时针旋转力矩解耦缸转子（驱动缸定子），使容腔I体积减小ΔV，达到平衡状态，即相当于力矩解耦缸与水动力在驱动缸转子上产生大小相等、方向相反的力矩，合力矩为零，达到解耦目的。同理，在合外力矩为零时，驱动缸低速启动性能得到极大提升，系统时滞降到最小。此外，在复式液压摆动缸运动过程中，内外层转子同向旋转，内层转子与外层转子的相对非饱和线性区间不变，但内层转子的绝对非饱和线性区间是增大的，即舵叶有更大的转角范围；内外层转子反向旋转，可使舵叶及时制动、换向，提升舵机操纵的灵活性，以备紧急转向。

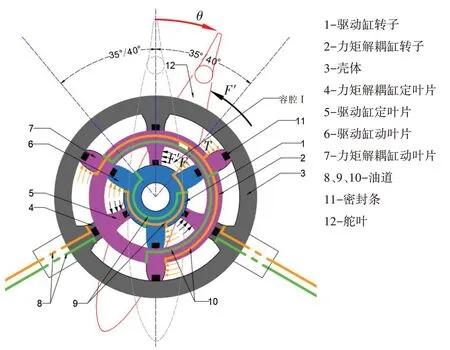
图1 复式液压摆动缸工作原理图Fig.1 Operational principle diagram of compound swing cylinder

1.2 复式液压摆动缸结构设计

复式液压摆动缸主要结构包括：上下端盖、外部壳体、驱动缸转子、力矩解耦缸转子、动叶片、静叶片等，图2 为复式摆动缸的结构示意图。图中参数含义为舵杆直径D1、复式摆动缸壳体内径D5，复式摆动缸壳体直径D4、力矩解耦缸转子内径D3、驱动缸转子轮毂直径D2、动静叶片高度H、动静叶片宽度B和壳体（包括端盖）厚度s。

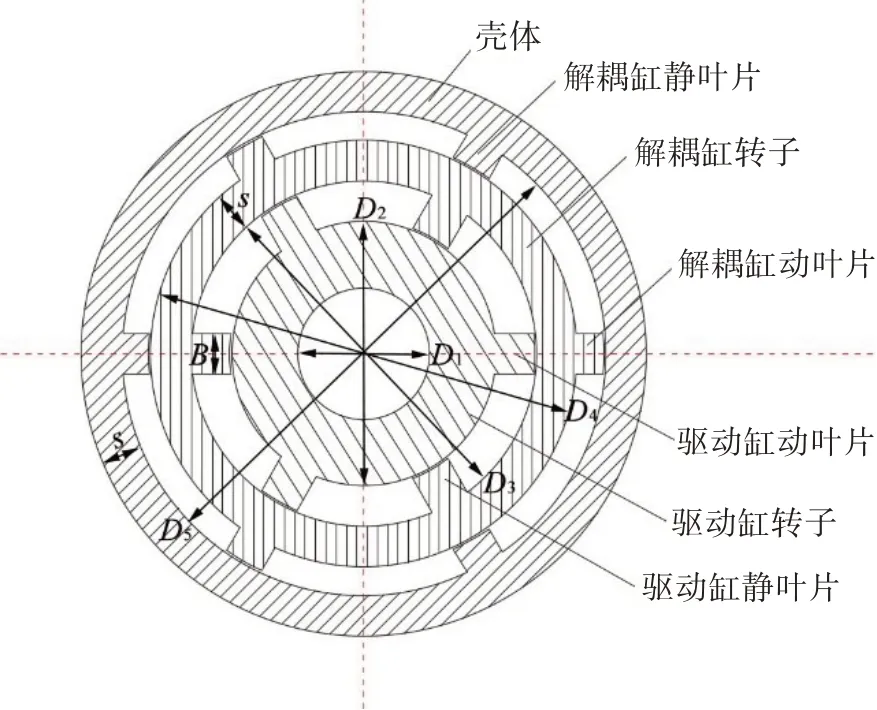
图2 复式液压摆动缸结构示意图Fig.2 Structure diagram of compound swing cylinder

2 基于协同进化多目标遗传算法的复式摆动缸结构设计

遗传（Genetic Algorithm，简称GA）算法是一种模拟生物进化理论中的自然选择和遗传学机理的生物进化过程的计算模型，一般来说，设计变量、目标函数和约束条件是优化设计的三大要素。本文以质量最小为寻优目标，在满足弯曲强度、挠度和许用壳体变形量的同时，输出扭矩不小于500 kN·m。

2.1 结构参数的优化设计

（1）设计变量

依据上述复式液压摆动缸的结构设计要求，以舵杆直径D1=0.36 m，复式摆动缸壳体内径D5、力矩解耦缸转子内径D3、驱动缸转子轮毂直径D2、动静叶片高度H、动静叶片宽度B和壳体（包括端盖）厚度s为设计变量，可表示为

（2）设计目标

根据复式摆动缸设计的已知条件和对其性能指标的要求，以质量最小作为优化目标[10]，即

式中：m为复式液压摆动缸质量，单位为kg；ρ为材料密度，单位为kg/m3；V为复式液压摆动缸的总体积，单位为m3。

忽略加强肋板等结构细节，复式液压摆动缸的体积可表示为

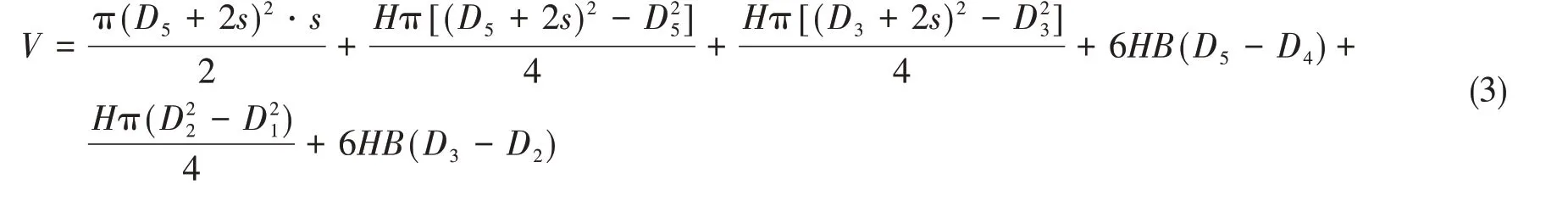
安装在外部壳体上的静叶片和与内外层转子一体铸造加工的动叶片，其受力可简化为悬臂梁模型，优化设计的前提是满足弯曲强度和挠度约束条件。

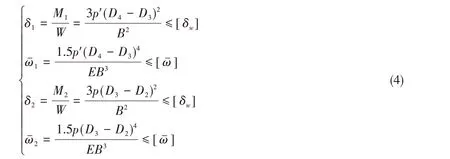
式中：p′为力矩解耦缸油腔油压，单位为Pa；p为驱动缸油腔油压，单位为Pa；[δw]为许用弯曲疲劳强度，单位为Pa；E为弹性模量，单位为Pa；[ωˉ]为叶片许用挠度，单位为m。

设计要求复式液压摆动缸的内外层转子输出转矩T均不小于500 kN·m，即

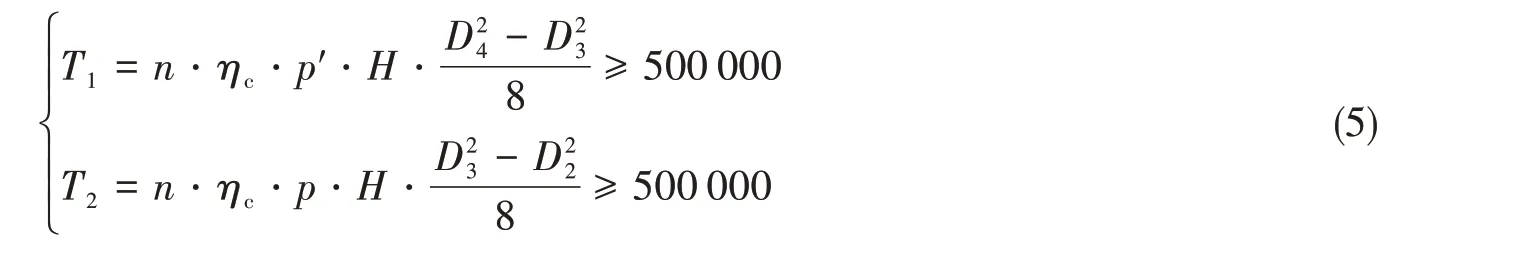
式中：n为动叶片的数量，n=3；ηc为复式摆动缸容积效率，ηc=0.9。由壳体变形公式可知

（3）约束条件

根据常规经验选取和实际空间结构的限制，设计变量的取值范围如表1所示。

表1 设计变量取值范围Tab.1 Range of design variables

复式液压摆动缸的结构优化可以视为求解由12个不等式联立的方程组描述的多维约束问题，共涉及到6个变量。非线性约束条件下的优化问题可用如下函数表示[11]：

2.2 协同进化模型的多目标遗传算法设计

在遗传算法的基础上，采用基于协同进化原理的多目标[12-14]遗传优化（Co-evolutionary Multi-objective Genetic Algorithm，简称C-MGA）算法，同时考虑不可行解违反约束的总量和各不可行解违法约束的个数两种信息，基于协同进化模型选择罚因子，并将其作为寻优变量，在搜索过程中利用算法自适应地进行调整，在解空间进化探索决策解的同时也在罚因子空间进化探讨罚因子，最终使算法同时获得约束优化问题的最优解和最佳罚因子。

进化过程描述如下：

C-MGA 包含两类种群，一类种群包含m个子种群Swarm1，j（j=1，2，…，m），子种群规模均为n，种群中的每个个体Ai（i=1，2，…，m）表示问题的一个决策解，该类种群用于进化决策解；另外，还有一个规模为m的种群Swarm2，其每个个体Bj（j=1，2，…，m）代表一组罚因子，用于计算Swarm1，j中各个体的罚函数值（或称适配值）。即第一类种群Swarm1，j用GA 来进化解向量，第二类种群Swarm2 则用GA来调整罚因子。

（1）Swarm1，j中每个个体利用Swarm2 中的Bj表示的罚因子计算适配值，并连续采用GA 算法进化G1代获得一个新的解的种群Swarm1，j；

（2）根据Swarm1，j中所有解的优劣信息，评价Swarm2 中个体Bj的优劣，评价罚因子；

（3）当Swarm2 中所有个体Bj均得到评价后，Swarm2 采用GA 算法进化一代，从而获得新的种群Swarm2，即得到m组新的罚因子；

（4）在一代协同进化结束后，Swarm1，j（j=1，2，…，n）再分别用新的m组罚因子进行评价，以此类推，直到满足算法终止准则，例如达到给定的最大协同进化代数G2；

（5）算法通过比较所有Swarm1，j得到历史最好解，将最优者作为最终解输出，同时算法输出终止时Swarm2中的最优罚因子。

C-MGA算法的框架如图3所示。

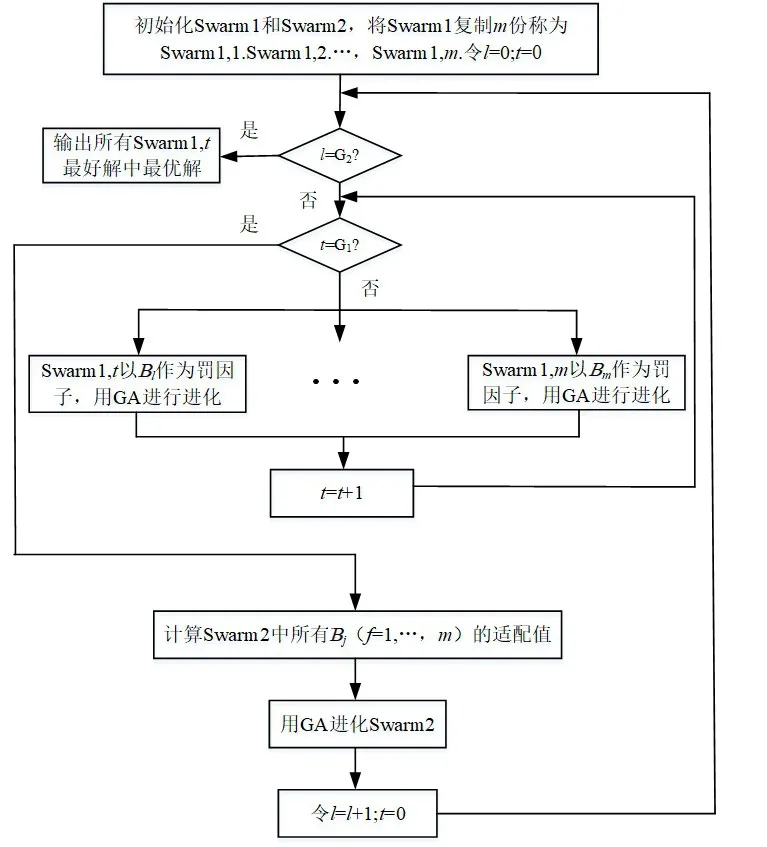
图3 C-MGA优化算法流程图Fig.3 Flow chart of C-MGA optimization algorithm

2.3 结果分析

算法中种群规模M、交叉概率pc和变异概率pm三个参数尤为重要。在复式液压摆动缸尺寸参数优化过程中，由于非线性约束条件过多，使得可行域空间较小，在惩罚机制下，迭代进化较快进入可行域并收敛到稳定值。算法选取种群大小为100、交叉概率为0.6、变异概率为0.001。设定算法的进化终止条件为进化过程中连续10代种群之间的适应度函数平均值变化小于设定值0.001或达到最大进代数（最大进化代数设定800）。

使用GA 算法求解三次，其迭代进化曲线如图4所示（图中点划线表示种群平均值，实线表示种群最佳值）。

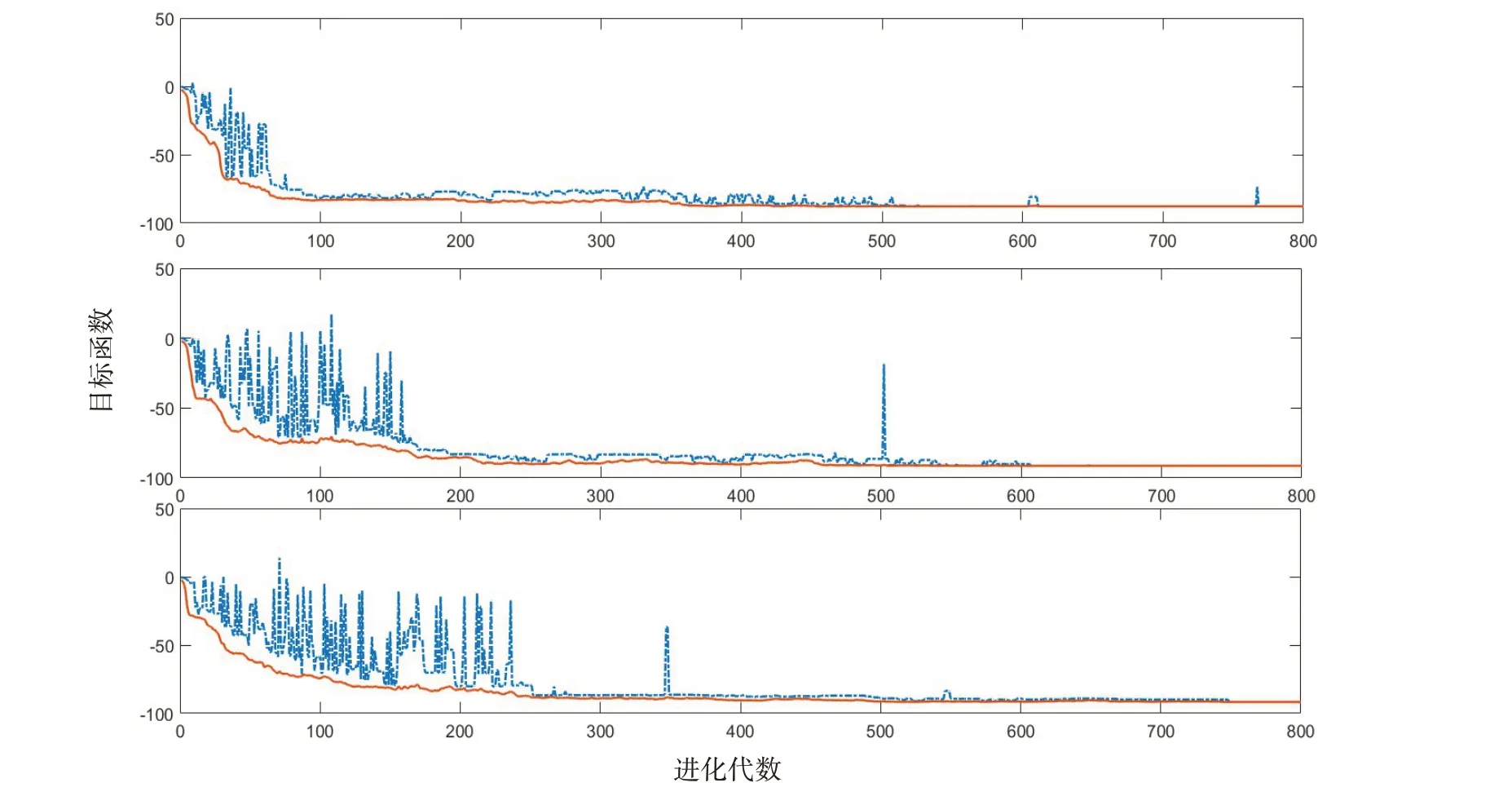
图4 GA迭代进化曲线Fig.4 Iterative evolution curve of GA

曲线表明，随着迭代次数的增加，虽然种群平均值不断趋于种群最佳值，但是大概都是在第520代、610代、750代达到连续10代种群之间的适应度平均值变化小于0.001，通过传统的GA算法找到满足目标函数的最佳个体与C-MGA 算法求解结果相比相差较大，这是因为GA 算法无法自我调整罚因子来指导种群的搜索，容易陷入局部最优解，无法跳出，且收敛速度慢，求解时间长。

使用C-MGA 算法求解三次，其迭代进化曲线如图5所示（图中点划线表示种群平均值，实线表示种群最佳值）。

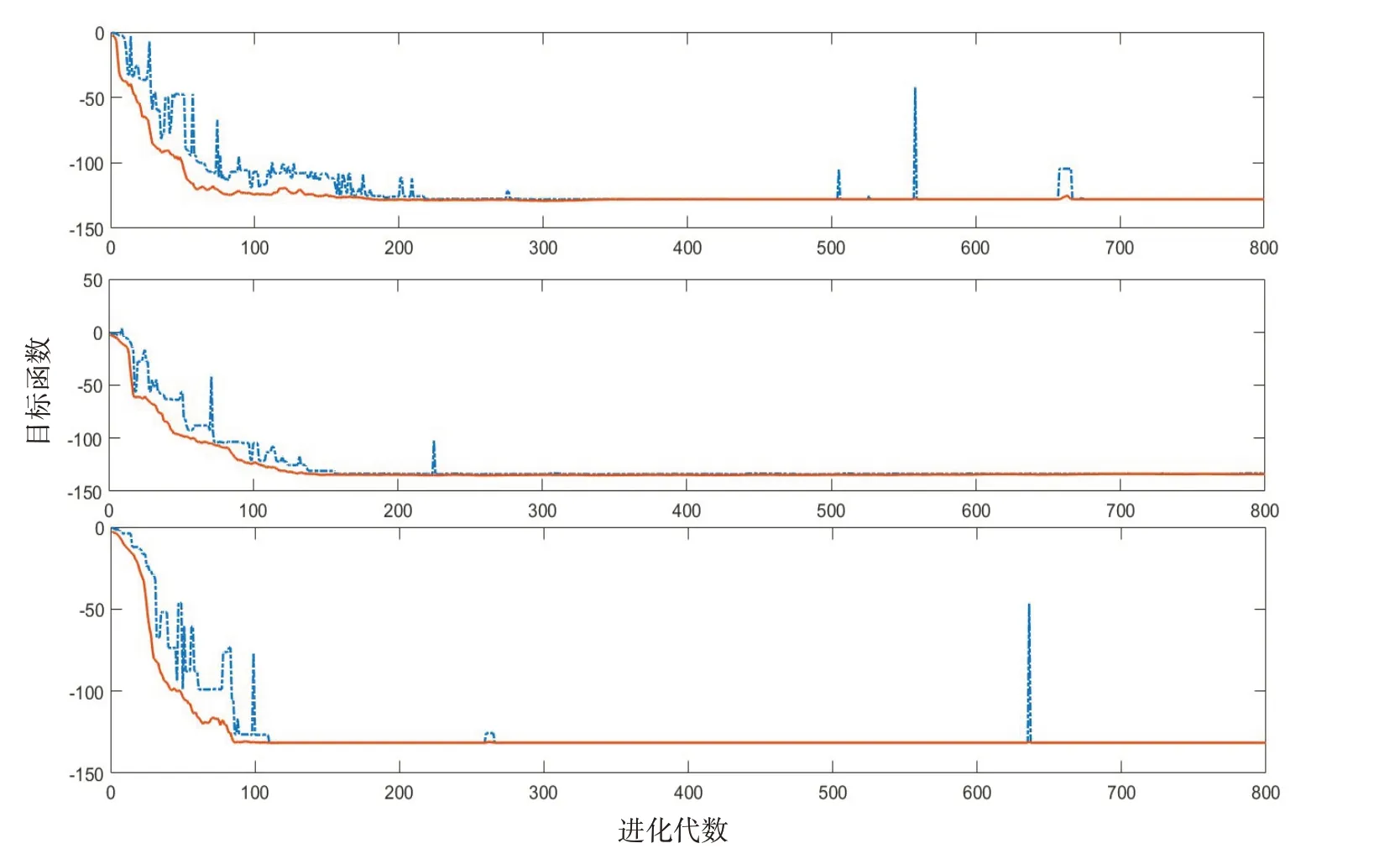
图5 C-MGA迭代进化曲线Fig.5 Iterative evolution curve of C-MGA

可以发现随着迭代次数的增加，种群平均值不断变化，在当种群进化到大约第220代、160代、110代时，之后连续10代种群之间的适应度平均值变化小于设定值0.001，几乎无偏差且趋于稳定，偶有变异偏离最佳值后仍能迅速收敛，说明找到了满足目标函数的最佳个体，终止进化。

对比传统GA 算法，由于C-MGA 算法同时考虑协同进化模型中的不可行解违反约束的总量和各不可行解违法约束的个数两种信息，在搜索过程中利用算法自适应地进行调整罚因子指导自身的搜索，把搜索得到的经验与其他种群分享，最终使算法同时获得约束优化问题的最优解和最佳罚因子，收敛速度快、收敛效果好，当遇到局部极小的情况时能够迅速跳出，可以在解空间进行充分的搜索。

表2 为不同算法和不同规模种群，在交叉概率0.6、选择概率0.5、变异概率0.001 情况下，采用CMGA算法和GA算法进行求解所得出的最优解。

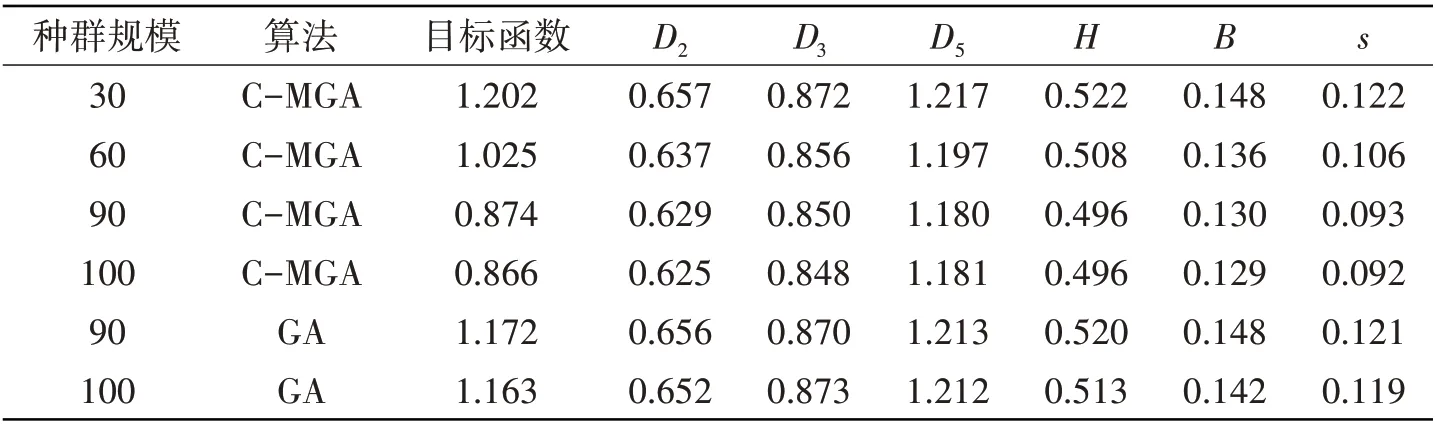
表2 不同算法和种群规模的优化结果Tab.2 Optimization results of different algorithms and population sizes

结果表明，不同的种群规模会产生不同的最优解值，当种群规模为30 时，其求解值最大，说明种群规模小的时候使得算法无法对解空间进行充分的搜索，容易在求解时陷入局部极小的情况；当种群规模为60时，扩大种群规模会对计算结果有明显的改善；当种群规模为90时，对比种群规模为100时表明，继续扩大种群规模对算法的性能几乎没有提升，这是因为种群的规模已经足够大，可以满足算法对解空间进行充分搜索的要求。通过对比种群为90和种群为100的两种算法优化的结果表明，GA算法在种群规模比较大的情况下才能与C-MGA 算法的小种群得到的结果相近，这是因为GA 算法是在计算之前设定的罚因子，在计算多目标、多约束问题下无法自我调整，使结果无法接近最优值。同为种群100 时，C-MGA 目标值与GA 目标值相比，其质量大概减少了25.5%。

根据舵机行业标准及尺寸规范，将优化结果进行圆整作为最终设计指标，优化结果如表3所示。

表3 优化结果及圆整结果（单位：mm）Tab.3 Optimization results and rounding results

用优化后的几何参数绘制出复式摆动缸的三维模型并根据工程经验在适当部位辅助加强筋，设计出内部油道，其三维图形如图6所示。

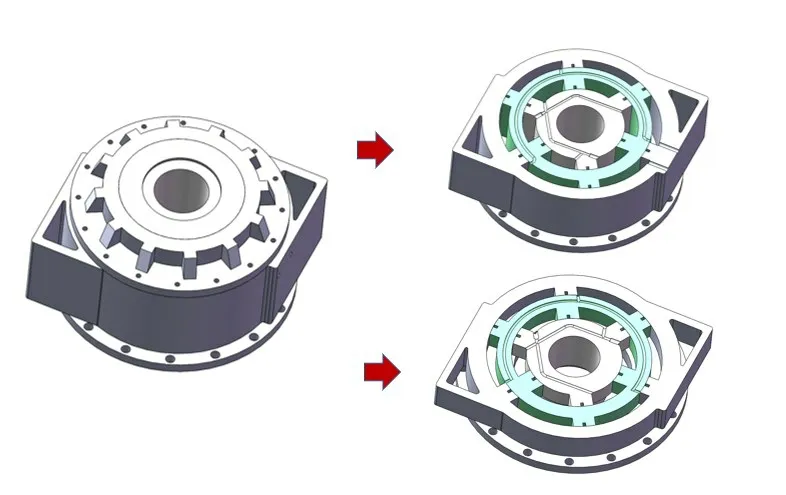
图6 复式液压摆动缸结构图Fig.6 Structure diagram of compound hydraulic swing cylinder

3 有限元分析

为验证用C-MGA算法优化后复式摆动缸的结构参数是否满足设计要求，通过有限元软件ANSYS对复式摆动缸外部壳体、驱动缸转子和力矩解耦缸转子三部分进行流固耦合分析。

以舵驱动缸转子为例，采用ANSYS Space Claim 软件构建舵驱动缸转子的内部流域，使用软件设置抽取流域的边界条件，设定进口压力为20 MPa、出口压力为0.1 MPa，将整个流域划分为边界、进油压力、出油压力和高低压腔四个部分，流场模型如图7所示。

图7 流场模型Fig.7 Flow field model

驱动缸转子的动叶片与其壳体所形成的间隙对流场的影响较大，为提高间隙内部的网格质量，保证流域计算的精准度和收敛性，在间隙较薄位置采用加密处理，增加单元格层数。在薄壁位置加密方式为独立网格划分，采用四面体单元划分网格，通过设置尺寸控制和边界条件，控制网格划分精度。对网格质量不达标的区域进行处理，使处理后网格质量满足Fluent 计算要求，流场网格划分如图8所示。

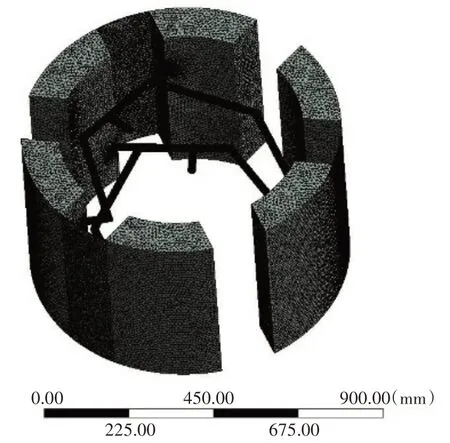
图8 流场网格划分Fig.8 Grid generation of flow field

同理可建立力矩解耦缸流场模型，对复式摆动缸内外层转子和外部壳体进行结构的有限元网格划分，选择独立网格，划分方式为四面体，另外流域的坐标与转动副的坐标在各自求解器中保持相同，使流体界面与相接触的结构界面保持对应。流体计算区域在Fluent 中进行稳态计算，求解出流场分布压力后，对固体结构域在ANSYS Workbench 中进行静态动力学分析。分析时设定所有部件的材料均为Q345C，其杨氏模量为200 GPa，泊松比为0.2，抗剪模量为79 GPa，屈服强度δ0.2=345 MPa，抗拉强度δb=600 MPa。假定整个部件工作在弹性范围之内，分析驱动缸转子从-35°转到+35°时整个部件的位移和应力。

图9 为θ=±35°时外部壳体的应力和位移云图，图10 为θ=0°时驱动缸转子的应力和位移云图，图11 为θ=0°时解耦缸转子的应力和位移云图。计算结果表明，外部壳体在高压腔容积最大的极限位置下（θ=±35°）受到的最大应力为111.73 MPa，最大位移量为0.056 mm；而驱动缸转子和解耦缸转子在θ=0°时产生最大应力和最大位移，驱动缸转子最大应力为151.53 MPa，最大位移量为0.201 mm；解耦缸转子最大应力为142.74 MPa，最大位移量为0.079 mm。

图9 外部壳体应力位移云图Fig.9 Stress and displacement nephogram of outer shell

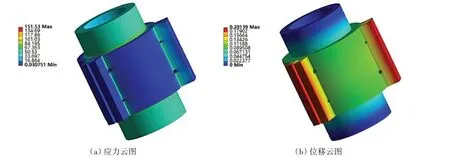
图10 驱动缸转子的应力位移云图Fig.10 Stress and displacement nephogram of rotor of driving cylinder

图11 解耦缸转子的应力位移云图Fig.11 Stress displacement nephogram of decoupling cylinder rotor

从位移云图上来看，最大位移发生在叶片顶端，这是因为此处留有密封槽，较其他位置壁薄，但位移量不大，满足设计需求。从应力云图来看，应力主要集中在叶片根部等形状突变处，该情况一方面是由于有限元在网格划分较细的情况下，应力难以收敛，在突然转角处，应力集中不可避免，实际加工时类似转角的位置可以设计过渡圆角以避免应力集中。通过比较整个部件所受到的最大应力值以及材料的屈服强度和抗拉强度，可以得出部件在20 MPa 的油压下的最大应力相当于屈服强度的1/2.3（即安全系数约为2.3）。