斜上坡和斜下坡地形条件下浮体波浪载荷的对比分析研究

伏耀华，张可成，赵 亮，刘晓雷

（1.上海船舶运输科学研究所，航运技术与安全国家重点实验室，上海 200135；2.中国舰船研究设计中心，武汉 430064；3.上海海事大学海洋科学与工程学院，上海 201306）

0 引 言

大多数情况下海底是不平坦的[1]，在岛礁附近或者近岸海域尤为明显，水深在较短的距离内可能变化几十到上百米。当波浪从外海传递到浮体布置区域时，受海底地形的影响将会发生绕射、反射和折射等现象，使得目标海域的波浪与开阔海域的波浪不同，呈现一定的非均匀性。另外，高低起伏的海底对浮体的水动力干扰也明显不同于平底，因此，海底地形对布置在其附近的浮体水动力响应的影响不可忽略[2]。已有学者经过试验研究证实了这一点，他们发现斜底条件下浮式平台的运动响应和平底时截然不同[3]。如果在工程设计过程中低估斜底的影响，可能会造成安全事故。

对于浮式结构物水动力问题，一般采用格林函数方法进行分析求解。主要思想是将满足偏微分方程的域问题转化为域边界的积分方程，从而将问题求解的维度降低。与其他求解方法相比，格林函数方法具有网格生成容易、方程组规模小和计算效率高等优点[4]。按照格林函数形式的不同，求解波浪中海洋平台摇荡运动的格林函数方法可以分为自由面格林函数法和Rankine源方法。

目前，已有众多学者分别给出了无限水深自由面格林函数不同形式的严格表达式[5-8]，并开发出相应的高效数值算法，包括级数展开、多项式逼近、制表法、多级展开法和基本函数近似等，无限水深自由面格林函数的数值求解方法已较为成熟。

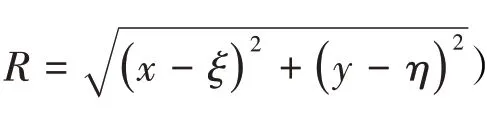
对于具有自由面的海洋结构物水动力问题，还可以选择Rankine 源作为基本解，将其分布在流场所有边界处，能处理复杂形式的线性或者非线性边界条件[16]。与自由面格林函数相比，Rankine 源方法的优势在于基本解的计算相对方便并且容易拓展到非线性问题中去，缺点是要在整个边界上分布源点，因此网格单元数量远大于前者，而且远场辐射条件处理比较困难。

对于无航速的浮体水动力问题，Yeung[17]在1973 年第一次采用频域Rankine 源法研究了浮体受迫振荡的二维和三维辐射问题，用一个虚拟的垂直控制面将流场分为内域和外域，内域边界上分布Rankine源，根据远场辐射条件采用特征函数展开法得到包含待定系数的外域速度势展开式，待定系数通过匹配内外域流场压力和速度的连续性进行求解。Bai[18]应用类似的远场辐射条件处理办法结合Rankine 源方法，研究了频率趋近于零和无穷时圆柱垂荡附加质量和阻尼系数的特性。Andersen 和He[19]重点关注远场辐射条件的处理，进一步发展了Yeung[17]的方法，研究了双体以不同方向、不同幅值和不同相位振荡时的二维辐射速度势。随后，Chau和Yuen[20]和Matsui等[21]对三维Rankine源方法的远场控制面条件进行了更加深入的讨论。需要指出的是，以上频域Rankine源方法都是基于远场水深均匀这一前提开展的，因为只有水深均匀才能建立远场速度势的特征函数展开式，从而满足远场辐射条件。

时域Rankine 源法比频域法的应用更加广泛，其既可以求解频域结果，也可以进一步引入非线性的边界条件研究非线性问题。与频域方法相同，时域Rankine源法计算时也需要引入一个虚拟的控制面将流场截断，从而形成有限的计算区域。但是数值模拟形成的波浪传播到截断边界处时会发生反射现象，与真实流场不一致，反射波也会影响浮体水动力载荷计算结果的准确性，因此，需要在截断面处设置合理的远场辐射条件，达到消除反射波的效果。水波问题中消除截断边界反射波最常用的一类方法是数值阻尼技术[22-24]，主要原理是在计算域外围设置一段阻尼区域，在这一段区域的自由面条件中加入阻尼项，当波浪经过阻尼区时能量会被耗散掉，从而起到消波的效果。根据实际需要，阻尼项会单独加入到运动学或者动力学条件中，或者在两个条件中同时加入阻尼项。MTF（multi-transmitting formula）是第二类方法，最早由以Liao 等[25]为代表的学者提出，随后被其他学者[26-27]成功应用到规则波浪和不规则波浪条件下浮体运动响应研究中。另一类非常有效的方法是内外域网格布置策略[28-30]，首先将自由面分为内域和外域，网格单元在内域等间距布置，外域网格尺寸以指数增长的形式向无穷远处扩张从而形成一个尺寸十分巨大的计算区域，只需要在波浪到达截断边界前完成数值模拟，就可以消除由于边界截断引起的反射波，避免了在自由面条件中加入人工阻尼，该方法最早是在无限水深问题中建立的。Feng等[31]将该网格布置策略拓展到有限水深平底条件下浮体二维水动力问题中，海底网格布置与自由面类似。

但是上述方法都是基于有限水深平底或者无限水深前提假设而建立的，不能直接应用于斜底条件下浮体水动力问题。为了处理上述问题，Feng等[32]基于Rankine源方法进一步提出了适用于斜底的内外域网格布置策略，并且研究了圆柱在斜上坡地形上的二维水动力系数。随后他们将该方法成功地应用到斜底条件下考虑流载荷的浮体二维水动力研究[33]。以上研究工作的主要内容是建立斜底条件下浮体水动力数值方法，但是他们只考虑了斜上坡对浮体水动力响应的影响。而在实际工程中海底崎岖不平，还会出现斜下坡的情形，因此有必要对其进行研究，以便全面地认识斜底地形对浮体水动力的影响。

本文以斜坡海底地形条件下的浮体为研究对象，采用基于台阶近似法和二维Rankine 源方法的SAM-RSM2D 模型求解斜坡条件下的入射波浪速度势和绕射速度势，通过对比斜上坡、斜下坡以及平底地形条件下浮体上的波浪激励力和激励力矩，详细研究斜上坡和斜下坡对波浪载荷影响的作用规律，讨论两者之间的区别与联系。

1 控制方程和边界条件

图1为斜底条件下浮体二维水动力问题示意图，不失一般性，假设水深沿x方向呈现任意变化，即水深变化的函数h不随y变化，左右两侧远场区域海底平坦，水深分别为hl和hr，但没必要相等，因此水深在海底中间区域变化，水深函数h(x)可以表示为

图1 斜底条件下浮体二维水动力示意图Fig.1 Two-dimensional hydrodynamic problems for the floating body over a sloping bottom

式中，x=a和x=b分别是中间斜底区域的起点和末端，x＜a和x＞b分别表示左侧和右侧平底区域。本文研究的流场边界由自由面SF、海底表面S0和浮体物面SB共同构成。

假设浮体的航速为零，基于理想、不可压缩和流动无旋的假设，流体质点的运动可以用波浪速度势来描述，对于二维问题，斜底条件下的波浪场速度势ϕ(x,z,t)可以分解为入射速度势ϕI(x,z,t)、绕射速度势ϕD(x,z,t)和辐射速度势ϕR(x,z,t)，即

其中，φ是速度势在频域中的表达式，Re表示取实部，ω是波浪频率。

波浪入射、绕射和辐射速度势φ均满足拉普拉斯方程：

线性化的自由面运动学和动力学边界条件为

式中，g是重力加速度。

海底不可渗透的条件为

式中，n0为海底处指向流场外的单位法向矢量。

考虑到绕射问题，浮体物面满足

另外，绕射速度势φD在远场有界，而且波浪向远方传播，可以表示为

式中，kl和kr分别表示左侧和右侧平底处波浪的波数。

2 斜坡海底条件下浮体二维水动力分析模型

本文采用SAM-RSM2D 模型求解斜坡海底条件下二维水动力问题的入射和绕射波浪速度势。由于斜浪时绕射速度势的控制方程不再是拉普拉斯方程，采用Rankine 源方法求解比较困难，因此本文仅考虑0°浪向的二维问题。本章将对本文涉及到的数值方法的主要思想以及分析步骤进行简要回顾。

2.1 入射波浪速度势

考虑规则波沿任意坡度的海底地形传播问题，在左侧平底上波浪幅值为A。对于斜底条件下的规则波，入射速度势φI满足以下拉普拉斯方程和各项边界条件：

按照台阶近似法的思路，将海底地形轮廓近似为一系列连续的台阶，每个台阶与自由面以及垂向界面构成对应的矩形子区域。如图2 所示，海底被近似为M个台阶，第m个矩形子区域的水深记为hm，在x方向从x=xm-1到x=xm，在z方向从z=-hm到z=0。因此，速度势φI可以表示为

图2 台阶近似法底部近似示意图Fig.2 Illustrative sketch of bottom approximation for SAM

其中，第1个和第M个子区域分别表示左右两侧平底区域。

对公式（9）应用特征函数展开法，得到流场第m个子区域的速度势特征函数展开式，可以表示为

其中，第n=1 项为传播模态，与波浪沿平坦海底传播的规则波入射速度势相同，剩余项是由斜底引起的非传播模态，Zm,n是模态函数，km,n是对应的特征值，通过匹配相邻子区域交界面上的压力和法向速度计算出未知数Cm,n和Dm,n，进而得到流场任意位置的入射波浪速度势。基于伯努利方程计算得到物面上的流体动压力，将动压力沿物面SB积分得到作用在浮体上的Froude-Krylov力FI。

2.2 绕射速度势

根据二维Rankine源方法，t时刻场点x′=（x′,z′）的绕射波浪速度势ϕ（x′,t）表示为

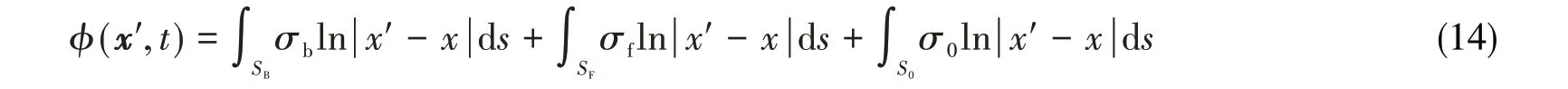
其中，x=(x,z)表示流场边界上的源点，σb、σf和σ0分别代表浮体物面、自由面和海底边界上源强。

在二维Rankine 源方法中，流场边界被离散成一系列连续的线元，假设每个线元上的源强定常。因此，上述积分方程可以近似表示为

其中，Sb,i表示物面上第i个线元，Sf,j表示自由液面上第j个线元，S0,k表示海底离散网格中第k个线元，Nb、Nf和N0分别代表浮体湿表面、自由液面和海底的线元数量。

其中，Δt表示时间步长，一般取为波浪周期的1/100，也可以根据数值试验得到。

利用上述时间步进方法，就可以计算出所有时间步的流场边界源强σb、σf和σ0，进而求解得到流场任意位置任意时刻的速度势ϕ(x′,t)。

基于伯努利方程结合绕射速度势ϕ(x′,t)，计算得到物面上的流体动压力p(x,y,z,t)，将动压力沿物面积分得到作用在浮体上的绕射载荷时历fD(t)。

在频率ω的入射波作用下的浮体，其绕射载荷在频域中的表达式，可以应用傅里叶变换计算得到，表示为

其中，FD,j表示绕射力在第j个方向上的分量，T0=2π/ω是浮体摇荡周期。

浮体在波浪中所受到的波浪激励力由Froude-Krylov力和绕射力组成：

3 浮体水动力模型和水深条件

本文选取Lee[34]研究的矩形浮体作为计算对象，吃水与浮体宽度相等，即d=L，纵摇运动的参考点位于浮体中心在静水面的投影。图3 和图4 分别表示将浮体分别布置在斜上坡和斜下坡不同位置正上方自由面处，其中P-1、P0和P1分别表示斜坡起点（深水）、斜坡中点和斜坡末端（浅水），即浮体形心在水平方向的坐标分别与P-1、P0和P1相对应，斜坡水平长度LS=b-a，平均水深为hm，斜坡高度为Δh=hl-hr。本文选取的斜坡地形参数为：LS=6d，hm=3d，Δh=0.8d，斜坡的倾角为22°。

图3 斜上坡地形上的浮体水动力Fig.3 Hydrodynamics of the floating body over the upslope bottom

图4 斜下坡地形上的浮体水动力Fig.4 Hydrodynamics of the floating body over the downslope bottom

4 结果与讨论

本文采用SAM-RSM2D 数值模型，基于Matlab 语言开发了相应的计算程序，分别对斜上坡和斜下坡上方的浮体波浪激励力进行计算对比分析。需要指出的是，为了体现斜坡地形对浮体所受到波浪载荷的影响，本章还给出了平底条件下波浪力计算结果作为对比，其中平底的水深与斜坡问题中浮体正下方的局部水深相等。

图5（a）给出了斜上坡和斜下坡P-1处浮体的纵荡波浪激励力，其中P-1处的局部水深为1.4hm。从图中可以看到：当频率（ω(L/g)1/2＜0.7 时，浮体在斜下坡P-1处纵荡波浪力与平底结果基本一致，而浮体在斜上坡P-1处纵荡波浪力相对稍大；相反，当频率（ω(L/g)1/2＞0.7时，浮体在斜上坡P-1处纵荡波浪力与平底结果基本一致，均小于浮体在斜下坡P-1处的计算结果。

图5（b）给出了斜上坡和斜下坡P0处浮体的纵荡波浪激励力，其中P0处的局部水深为1.4hm。从图中可以看到：当频率(ω(L/g)1/2＜0.7 时，浮体在斜下坡和斜上坡处纵荡波浪力均与平底结果基本一致；而当频率(ω(L/g)1/2＞0.7时，浮体在斜下坡处的纵荡波浪力大于平底结果，而斜上坡的计算结果则小于平底结果。

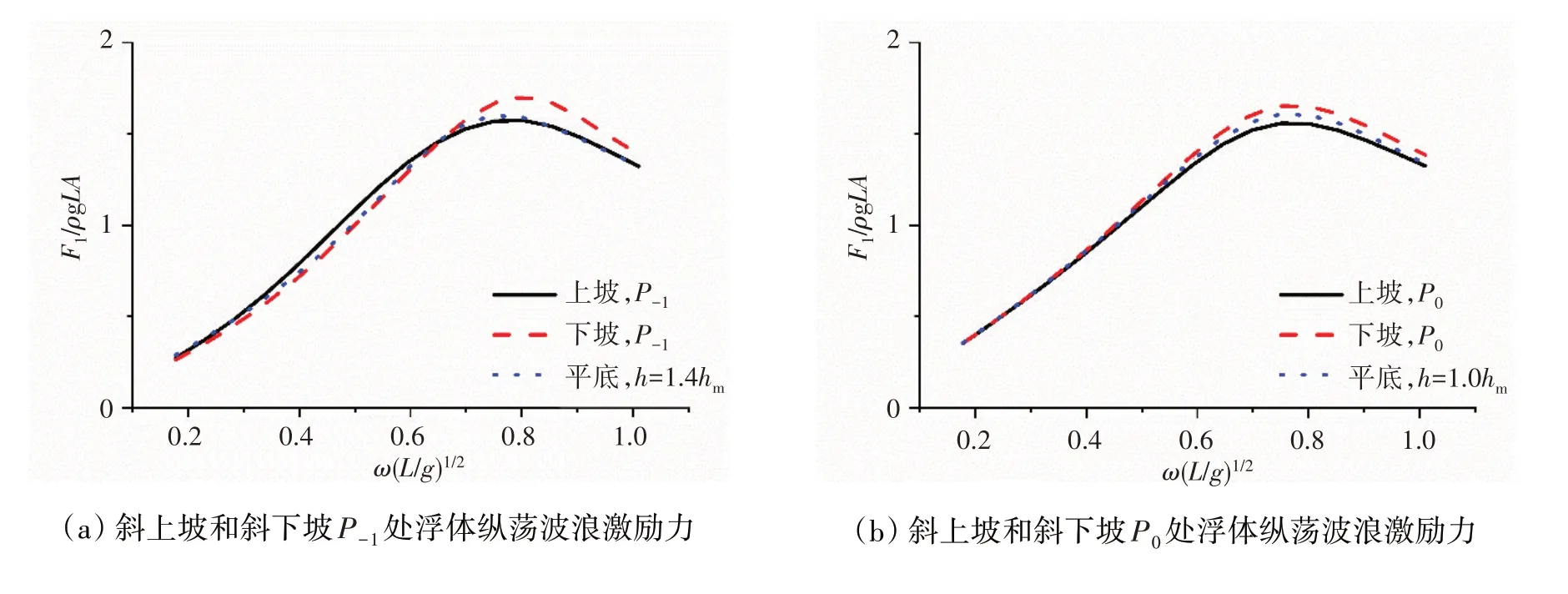
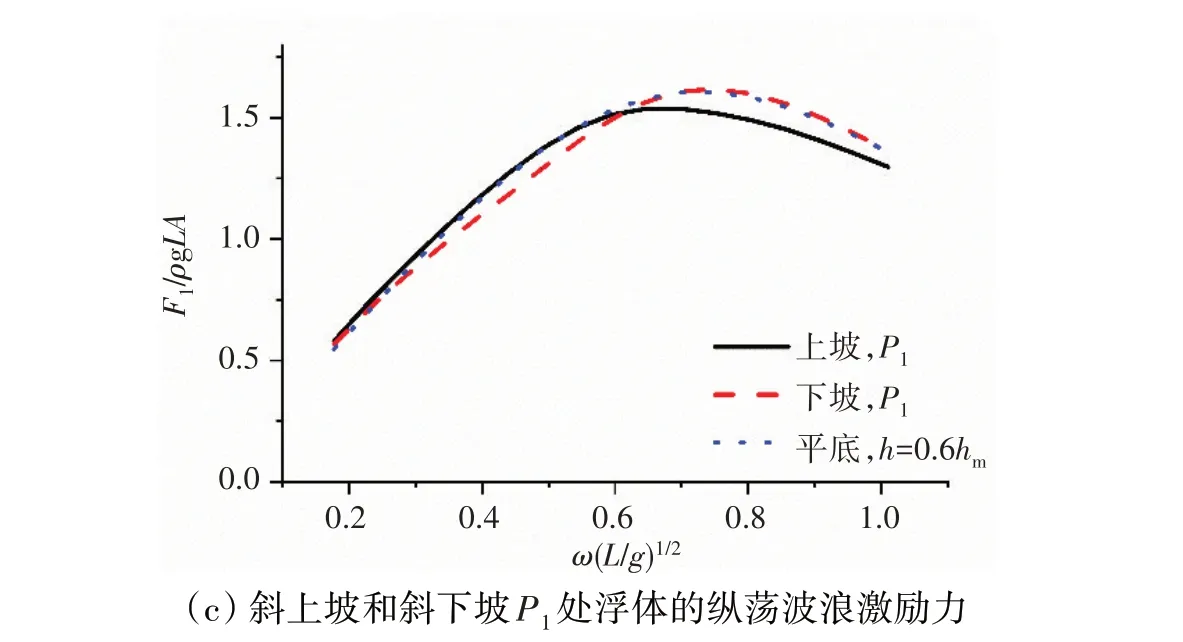
图5 斜上坡和斜下坡P-1、P0和P1处浮体纵荡波浪激励力Fig.5 Surge wave exciting force of P-1,P0,P1 over the upslope and downslope bottoms

图5（c）给出了斜上坡和斜下坡P1处浮体的纵荡波浪激励力，其中P1处的局部水深为0.6hm。从图中可以看到：当频率(ω(L/g)1/2＜0.7 时，浮体在斜上坡处纵荡波浪力均与平底结果基本一致，稍大于斜下坡的计算结果；而当频率(ω(L/g)1/2＞0.7 时，浮体在斜下坡处的纵荡波浪力与平底结果基本相等，而斜上坡的计算结果则明显较小。

结合图5（a）、（b）和（c）可以看到，对于浮体的纵荡波浪力，低频时斜上坡和斜下坡以及平底的计算结果较为接近，而高频时斜下坡的计算结果明显高于斜上坡时。原因在于低频长波绕射能力相对更强，因此水质点的纵荡运动受斜坡地形影响较小；而高频短波时，斜下坡将水质点的垂向运动反射成向前的纵荡运动，因此斜下坡的纵荡波浪激励力更大。

图6（a）、（b）和（c）分别给出了斜上坡和斜下坡P-1、P0和P1处浮体的垂荡波浪激励力。从图中可以看到：当频率(ω(L/g)1/2＜0.5 时，浮体在斜上坡P-1处垂荡波浪力高于平底结果，浮体在斜下坡P-1处波浪力最小。原因可能在于波浪向前传播时，水质点的水平运动被斜上坡反射成垂向运动，作用在浮体下方引起垂荡波浪激励力增大；而斜下坡会将水质点的垂向运动反射成水平运动，因此垂荡运动减小，波浪载荷减小。而当频率(ω(L/g)1/2＞0.5 时，斜上坡和斜下坡的计算结果均与平底结果接近，即高频垂荡波浪载荷受斜坡地形影响较小。这主要是因为高频波长较短，水质点运动到海底处时垂向速度相对较小，受海底地形影响也相应较小。

图6 斜上坡和斜下坡P-1、P0和P1处浮体的垂荡波浪激励力Fig.6 Heave wave exciting force of P-1,P0 and P1 over the upslope and downslope bottoms

图7（a）、（b）和（c）分别给出了斜上坡和斜下坡P-1、P0和P1处浮体的纵摇波浪激励力矩。从图中可以看到，海底地形对浮体波浪激励力矩的影响与其对纵荡波浪力的作用相似，具体体现在：低频时浮体在斜上坡、斜下坡和平底的计算结果相对比较接近；而高频时在P-1处斜上坡的结果与平底基本一致，而在P1斜下坡的计算结果与平底非常接近。这是因为斜坡地形引起的浮体波浪激励力矩变化主要是由浮体上水平方向波浪载荷的改变引起的，即斜底改变了浮体两侧波浪载荷的不对称性。

图7 斜上坡和斜下坡P-1、P0和P1处浮体的纵摇波浪激励力矩Fig.7 Pitch wave exciting moment of P-1,P0 and P1 over the upslope and downslope bottoms

5 结 论

本文采用台阶近似法和二维Rankine 源方法建立了斜坡海底条件下浮体二维水动力数值模型（SAM-RSM2D），开发了对应的软件程序。随后应用该模型对斜上坡、斜下坡和平底地形条件下的浮体波浪激励力和激励力矩进行了对比分析，研究发现：

（1）对于纵荡和纵摇波浪激励力，当浮体布置在深水区时，斜下坡低频计算结果与平底接近，但小于斜上坡时，后两者高频结果基本一致且小于斜下坡时；当浮体布置在斜坡中心处时，三者低频结果基本一致，斜下坡高频结果最大而平底结果次之；当浮体布置在浅水区时，斜上坡低频计算结果与平底接近且大于斜下坡时，斜下坡与平底高频结果基本相等且大于斜上坡时。

（2）对于垂荡波浪激励力，在任意浮体布置点，斜上坡低频计算结果高于平底，斜下坡结果最小，而三者的高频结果比较接近。

下一步将进一步考虑复杂海底地形对浮体波浪载荷的作用机理，为实际工程中近岸和岛礁附近的浮体波浪载荷预报提供支持。