非回转体艇型参数化构型及自动建模计算方法研究
2022-12-01彭亮斌吴有生俞孟萨白振国
彭亮斌,吴有生,俞孟萨,白振国
(1.中国船舶科学研究中心船舶振动噪声重点实验室,江苏无锡 214082;2.深海技术科学太湖实验室,江苏无锡 214082)
0 引 言
传统潜艇艇型主要以水滴型为主,随着水下技术发展与功能任务使命的不断拓展,水下平台逐渐向大深度与多任务负载等方面发展,非回转水滴型艇型平台越来越成为未来水下装备技术发展的一个重要方向,比较常见的非回转水下平台主要呈现出横剖面为非圆形剖面与双尾扁平外形的典型特征。
船体参数化构型与自动建模计算技术是船型优化设计的关键环节,在船舶优化设计过程中,首先对船体几何进行参数化表达,利用尽可能少的参数实现船体几何重构,建立艇型表达参数与优化过程中设计变量之间的联系。按照艇型参数化形式的不同,船体构型方法可分为两种:一种是基于船型参数(如长宽比、方形系数等),它通过一系列表示船体几何特征参数的变化来实现船体构型,如Lackenby 变换方法、参数化模型方法等;另一种是基于几何造型技术,它主要通过一系列控制点位置的变化来实现船体曲面的变形与重构,如Bezier Patch 方法、自由变形方法、基于CAD 方法等。回转体艇型的参数化一般是由公式给出首尾形状曲线,并根据需要决定是否使用平行中段。常用的首尾形状有Myring 型、Nystrom 型、Granville 型、鱼雷型和水滴形等。国内外主要针对水滴型潜艇、鱼雷、AUV 等回转体艇型参数化开展了大量研究工作。1976年,沈泓萃等[1]采用因子分析方法和矩阵推导出了回转体的多项式表达式,建立了使用艇型参数表达水滴形线型参数化方法,分析了艇型参数对线型的影响,为水滴形航行体优化奠定了基础;2005年,美国弗吉尼亚理工大学Chin等[2]在开展非传统新概念作战潜艇概念方案研究时,采用了理想简化的艇型进行参数化,艇型艏部采用半球直径,平行中体长度、艇型艉部长度、型宽和型深作为可变化的设计变量,进行了适应近海的型宽和型深比优化设计。
80 年代,法国ONERA 提出了扁平体模型、NNemo 模型、DTMB 66 系列模型三个系列模型,主要对扁平非回转体艇型的流场、阻力与操纵性能进行了数值计算与试验[3~4];2005 年,Racine 等[5]采用重叠网格与六自由度运动方程相结合的方式对NNemo模型的操纵性进行了数值模拟;2006年,Demoss等[6]从尾迹、边界层和艇型摩擦系数等角度对NNemo模型的阻力性能开展了大量的试验工作,比较了围壳位置对阻力的影响;2008年,美国海军水面作战中心(NSWC)的泰勒水池开展了非旋转体扁平状外形的自航模模型试验及线型优化设计,Roddy 等[7]在第27 届ONR 会议上公布了关于非旋转体潜艇模型水动力研究的进展,对NNemo模型进行了回转操纵试验,并采用神经网络的预测方法对模型操纵运动进行了预报;2009年,Demoss等[8]针对扁平体选定区域的边界层、壁面摩擦系数、尾迹和二次流动速度剖面进行了试验,并利用测量的数据对模型的升力和阻力进行了评估;2009 年,Granlund 和Simpson等[9]对扁平艇型的操纵性进行了研究,对不同攻角和漂角下的定常力进行了测量,同时利用动态俯仰机构对非定常的俯仰运动进行了试验;2010年,泰勒水池对非回转体(NBOR)艇型操纵性能进行了预报,通过拘束模型参数试验对不同宽高比、长宽比、尾部形状等几何变化对非回转船体的水平面及垂直面稳定性和控制的影响进行了分析,并发展了DTMB 66 系列模型[10];2011 年,Delaney[11]采用RANS方法对DTMB 66系列模型进行了数值计算,从阻力和操纵力进行了分析,得出了非回转艇型在垂直平面内提供更大升力的结论。
综上所述,对于非回转体艇型研究,国内外主要针对某些特定离散模型对象开展了一些数值与试验研究,但基于艇型参数化表达理论方法的计算研究很少有涉及,非回转体艇型缺乏相应的理论方法与技术。为了解决船型优化中快速自动构型与计算的关键技术,为参数化艇型构型与快速计算建立理论方法,本文开发了相应算法与软件,并验证了理论方法与算法程序的有效性。
1 非回转体艇型参数化构型数学模型
1.1 非回转体艇型特征参数
艇体外形影响水下平台的水动力性能、水动力噪声、目标强度等总体性能,寻找一种适用于非回转体艇型的表达方法,可以建立船体表达参数与设计优化之间的联系,以便系统开展艇型理论与试验研究。目前,传统回转水滴型艇型主要通过二维曲线回转得到,艇型中纵剖线对应的二维曲线常用多项式函数进行表达。而扁平艇型属于非回转体三维艇型,其艇型线型不能仅用一条二维曲线进行表达,型线表达更为复杂,目前还没有形成有效的参数化表达方法。传统复杂艇型表达方法主要通过离散的型值点生成不同方向的剖线,进而生成艇型曲面,该方法的缺点是需要大量型值点才能进行较为精确的表达。
本文主要针对的是非回转复杂三维立体艇型,基于艇型横剖线、最大水线和中纵剖线三个方向的剖线艇型特征参数,采用数学方程表达型线的方法,进而生成艇型曲线曲面。该方法表达较为精确,且需用到的参数数量较少,可以快速变换生成非回转体艇型。非回转体艇型横剖线、最大水线和中纵剖线三个方向剖线对应的特征参数如表1所示。

表1 非回转体艇型特征参数Tab.1 Characteristic parameters of non-body-of-revolution hull
本文艇型型线表达采用艇型标准直角坐标系Oxyz,其中,原点O纵向位置取在艇型头部,垂向位置取最大水线高度位置,x轴、y轴和z轴正方向分别指向艇型尾部、右舷和垂直向上。同时,型线采用了艇型归一化坐标系Oξηζ。艇型型线数学表达采用艇型表达坐标系如图1所示。
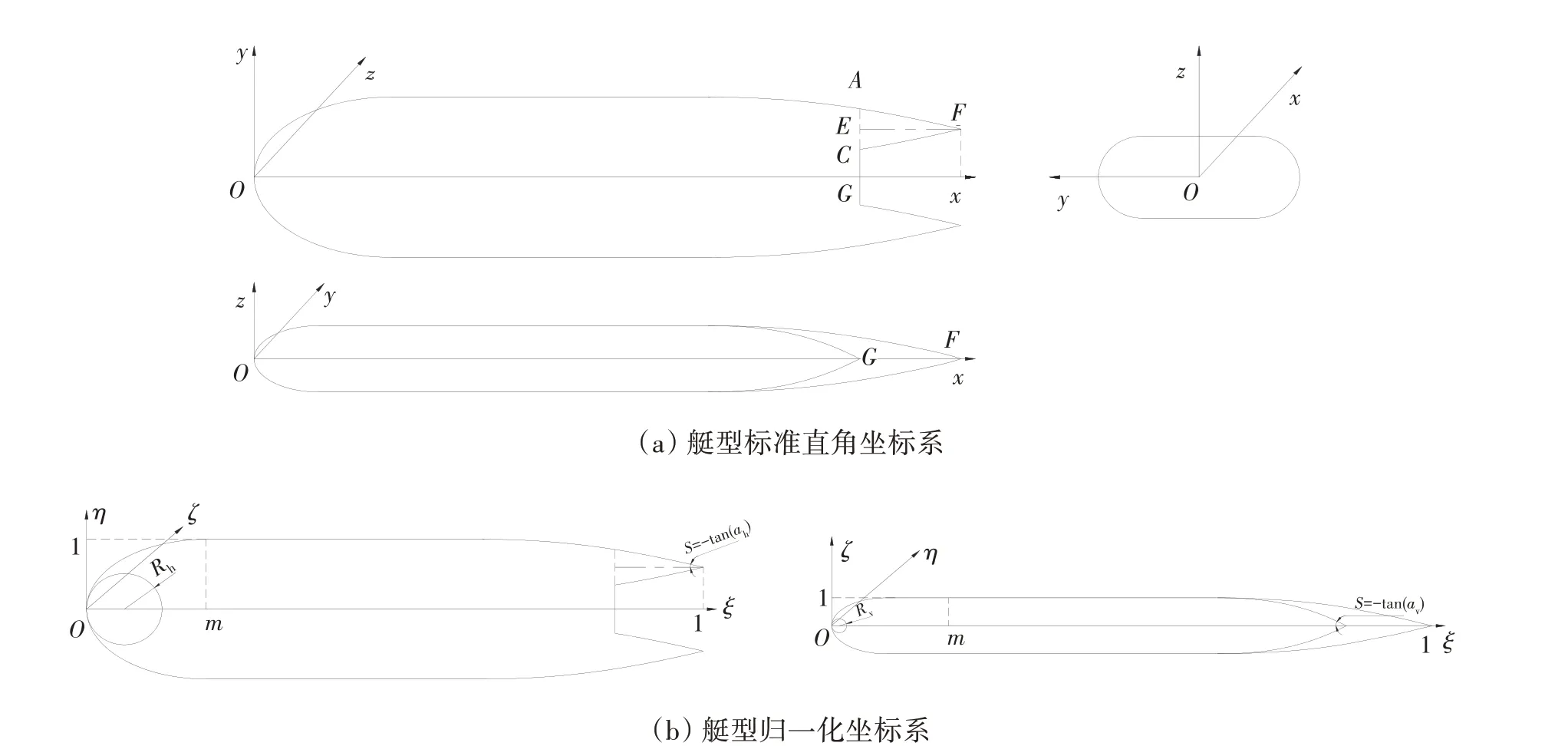
图1 艇型表达坐标系Fig.1 Coordinate systems used to express the hull form
1.2 横剖线及其数学表达方程
1.2.1 横剖线形式及特点
非回转体艇型平行中体典型横剖面为非圆横截面,归纳分析平行中体典型横剖面存在的可能形状及特点,按照横剖面剖线数学表达不同进行分类,典型横剖面如图2所示。

图2 平行中体典型剖面剖线组合线型Fig.2 Typical section hull forms of the parallel middle body
(1)椭圆形:艇型横剖线为椭圆,艇型型线较简单,艇型一般用于双壳体结构形式,该艇型结构加工难度比较小,对保持艇型流线形外形有好处,有利于舷间设备的布置,但是舷间无效空间较大,利用率相对较低,不利于艇型性能的提高。
(2)圆弧+直线拼接形:艇型横剖线为椭圆弧加直线组合形式,艇型型线较简单,艇型一般用于单双壳体混合结构形式,该艇型结构加工难度比较小,舷间空间较小,不有利于舷间设备的布置,有利于控制排水量与提高性能。
(3)圆弧+椭圆弧拼接形:艇型横剖线为圆弧加椭圆弧组合形式,艇型型线较简单,艇型一般用于单双壳体混合结构形式,该艇型结构加工难度比较小,有利于舷间设备的布置,可以选择合适的型高,既满足设备布置要求,又满足控制排水量要求,有利于艇型性能提高。
(4)任意样条形:艇型横剖线为封闭的样条曲线,艇型型线较复杂,艇型一般用于单双壳体混合结构形式,该艇型结构加工难度比较大,不利于控制排水量,不利于性能提高。
1.2.2 横剖线数学表达方程
上述分类艇型横剖线在直角坐标系Oxyz进行表达,其参数化数学表达方程描述如下。
(1)椭圆形
横剖面剖线为椭圆,横剖线可以表达为简单的椭圆方程:

式中,yb为横剖面剖线最大宽度的一半,zd为横剖线垂向对称轴处上下型线距离的一半。当横剖线为平行中体横剖线时,则yb=0.5B,zd=0.5D,对应图2(a)所示。
(2)圆弧+直线弧拼接形
一般情况,横剖面剖线为圆与椭圆相切拼接形,横剖线可以表达为左右圆方程和直线方程:

(3)圆弧+椭圆弧拼接形
当横剖面剖线为圆与椭圆相切时,横剖线可以表达为左右圆方程和椭圆方程:

式中,圆弧与椭圆弧相切点P坐标为(yP、zP),由此可以确定曲线,对应图2(c)所示。
(4)样条曲线形
对于复杂曲线的建模,NURBS 曲线方法提供了一个统一的数学表示,具有局部性质和描述复杂形状的优良性质。可以通过曲线上的若干型值点(yi,zi)反算得到控制点与及其对应的权值,从而实现NURBS曲线表达剖线。p次NURBS曲线定义为如下分段有理参数曲线。

1.3 最大水线归一化数学表达方程
最大水线是由左右舷对称曲线形成的一个封闭曲线,最大水线一半曲线由OAF、FC和CG三条线组成,如图1 所示。其中,CG为直线,FC为AF关于直线FE的对称,下面对最大水线外侧曲线OAF进行归一化参数化表达,归一化标准坐标系最大水线需满足的限定条件与参数条件如下:
(1)限定条件

式中,m为艇型最大横剖面相对位置,记为m=Le/Lah。
(2)参数条件

(3)假设最大水线方程
最大水线归一化数学方程采用多项式函数,表达如下:

式中,a0~a7为多项式待求解的系数。
(4)求解最大水线方程
将限定条件式(11)与参数条件式(12)代入到式(13),可以得到如下方程组:

由上述组成的方程组,含8个未知系数8个方程,可求解上述最大水线方程。
1.4 中纵剖线归一化数学表达方程
为了说明数学表达方法,本文以中纵剖线是由上下对称曲线形成的封闭曲线为例,对非上下对称的封闭曲线上下曲线分别进行表达,其表达方法类似。对中纵剖线一半曲线进行归一化参数化表达,需满足的限定条件与参数条件如下:
(1)限定条件
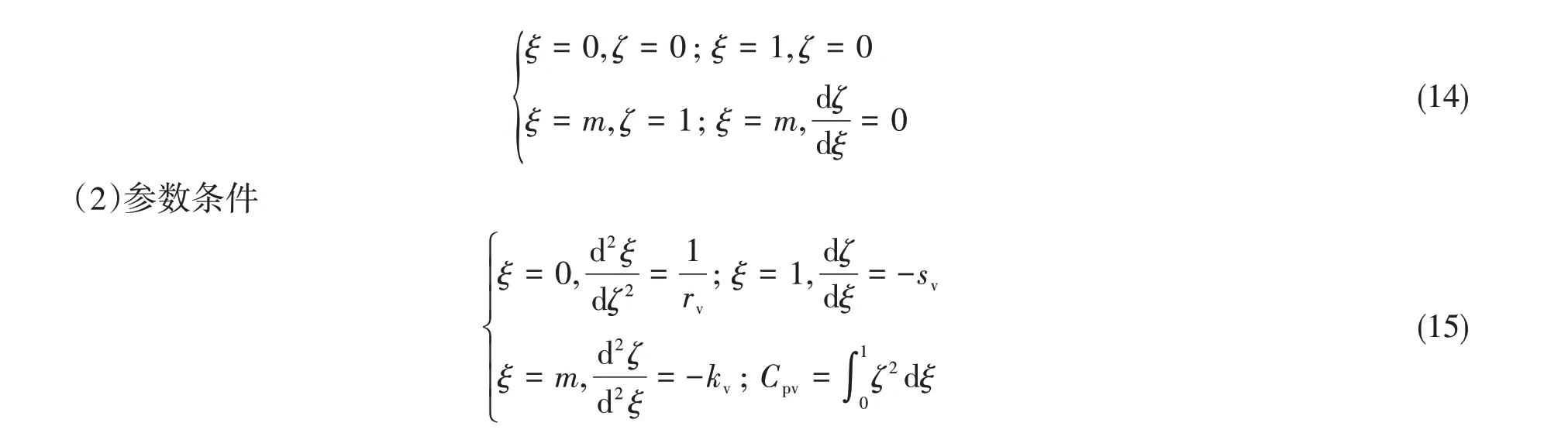
(3)中纵剖线方程
为了便于方程求解,将式(13)改写为如下中纵剖线归一化数学方程:

式中,R、S、K、P和Q是与艇型特征参数无关的多项式,r、s、k和Cp为多项式待求解的系数。
(4)求解中纵剖线方程
将限定条件式(14)与参数条件式(15)代入式(16),可以得到如下方程组:
上述组成的方程组含8个未知系数8个方程,利用多项式分析方法可求解中纵剖线方程。
1.5 艇型实际型线参数化表达
1.3 节和1.4 节描述的是艇型剖线归一化数学表达方程,利用如下所示的艇型归一化坐标和标准直角坐标系之间的转换关系,可以确定真实艇型剖线。

1.6 艇型曲面表达
由于NURBS 实现了解析曲面和自由曲面的统一表示,在曲面的定义与表达方面具有强大的功能,所以其应用最为广泛,已成为主流曲面表示方法。利用各NURBS 曲线上的控制点Pi,形成控制网格点Pi,j,利用u向p次和v向q次的NURBS曲面双参数分段有理函数[12]构造曲面,具有如下形式:
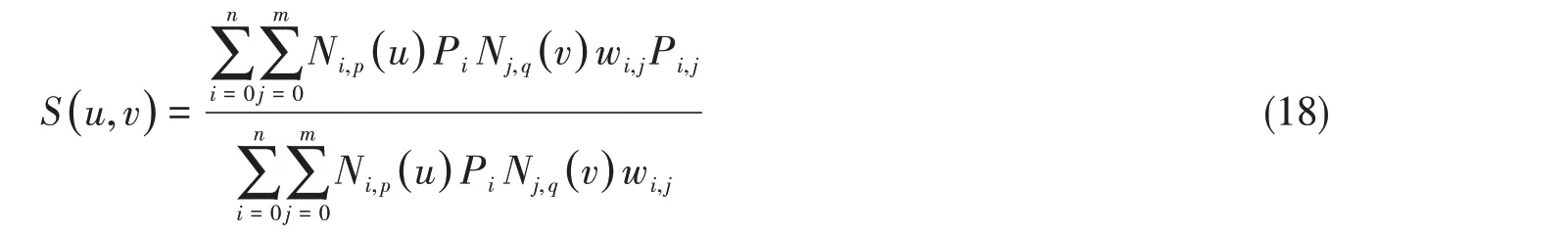
式中,Pi,j为控制网格,wi,j为对应的权值序列,Ni,p(u)、Nj,p(v)是定义在节点矢量

2 非回转体艇型参数化构型及建模计算程序的开发
2.1 艇型参数化构型流程方法
平行中体处剖线为规则形状圆弧直线拼接形,具有一定的现实代表性,为了便于说明研究方法,本文主要针对此型线构型及计算进行阐述。对于圆弧椭圆弧拼接形和样条曲线形,只是横剖面型线表达方程不同,但参数化构型及建模计算流程方法类似,同样适用此方法。
基于上述建立的非回转体艇型不同剖线数学方程,梳理非回转体艇型三维线型建模生成流程思路,建立了艇型剖线参数化表达方法,编制艇型生成算法程序。根据艇型构型设计要求,输入艇型不同特征参数,驱动生成艇型首中尾横剖线、中纵剖线与最大水线等型线,再通过生成的系列剖线,采用NURBS 曲面函数进行表达,放样得到首中尾部对应的三维曲面,从而快速生成对应尺寸参数的三维艇型,可用于艇型性能研究。通过艇型横向、水平向和纵向三个方向对应的横剖线、最大水线和中纵剖线的特征参数,采用数学方程参数化表达的方法对主要剖线进行表达,生成的归一化典型剖线如图3所示。通过曲面表达放样得到对应的三维曲面如图4所示。
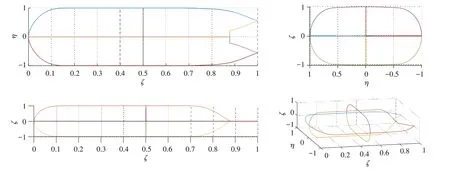
图3 参数化数学表达生成的剖线型Fig.3 Typical section forms by parametric mathematical expressions

图4 非回转体艇型三维参数化模型Fig.4 3D parametric model of non-body-of-revolution hull
2.2 艇型参数化构型及计算建模程序开发
基于上述非回转体艇型参数化表达理论方法,开发了相应的程序代码。同时,制定了非回转体艇型水动力建模计算流程,对参数化计算水域建模、网格划分与计算参数设定,编制了自动建模算法程序,对艇型参数化构型模块与自动建模模块之间的数据交换接口进行开发。采用Visual Basic 编写程序来调用艇型参数化构型与计算建模核心算法,并访问三维设计平台的组件对象,利用对象和属性获取、设置及处理数据的方法,开发了接口程序代码,并对计算得到的数据与模型进行统一化处理,搭建艇型参数化构型与自动建模计算程序框架,开发了计算程序软件平台,完成了软件程序界面的编制,如图5所示。
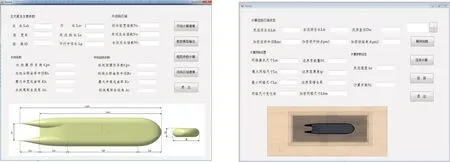
图5 非回转体艇型参数化构型与建模计算开发程序界面Fig.5 Software interfaces of 3D parametric model generation and hydrodynamic calculation
2.3 非回转体艇型三维构型与水动力计算验证
2.3.1 自动化构型验证
开发的艇型生成核心算法与接口程序,可以自动生成任意不同主尺度与扁平度的非回转体艇型,并输出得到相应的总体参数。为了考核验证艇型自动化构型模块程序的正确性,改变艇型总长和型宽,保证其他几何参数不变:来流段长Le=0.618 m,型宽D=0.305 m,最大水线菱形系数Cph=0.75,中纵剖面菱形系数Cpv=0.65,最大水线最大宽度处曲率Kh=0.000 25,中纵剖线最大高度处曲率Kv=0.000 5,最大水线头部曲率半径Rh=0.2 m,中纵剖线头部曲率半径Rv=0.1 m,最大水线艇型尾去流角ah=38o,中纵剖线艇型尾去流角av=24o。自动生成的不同扁平度参数的三维模型表面光滑、无瑕疵,能获得艇型的相应参数,证明了理论方法与算法程序的正确性,艇型系列构型如图6所示。
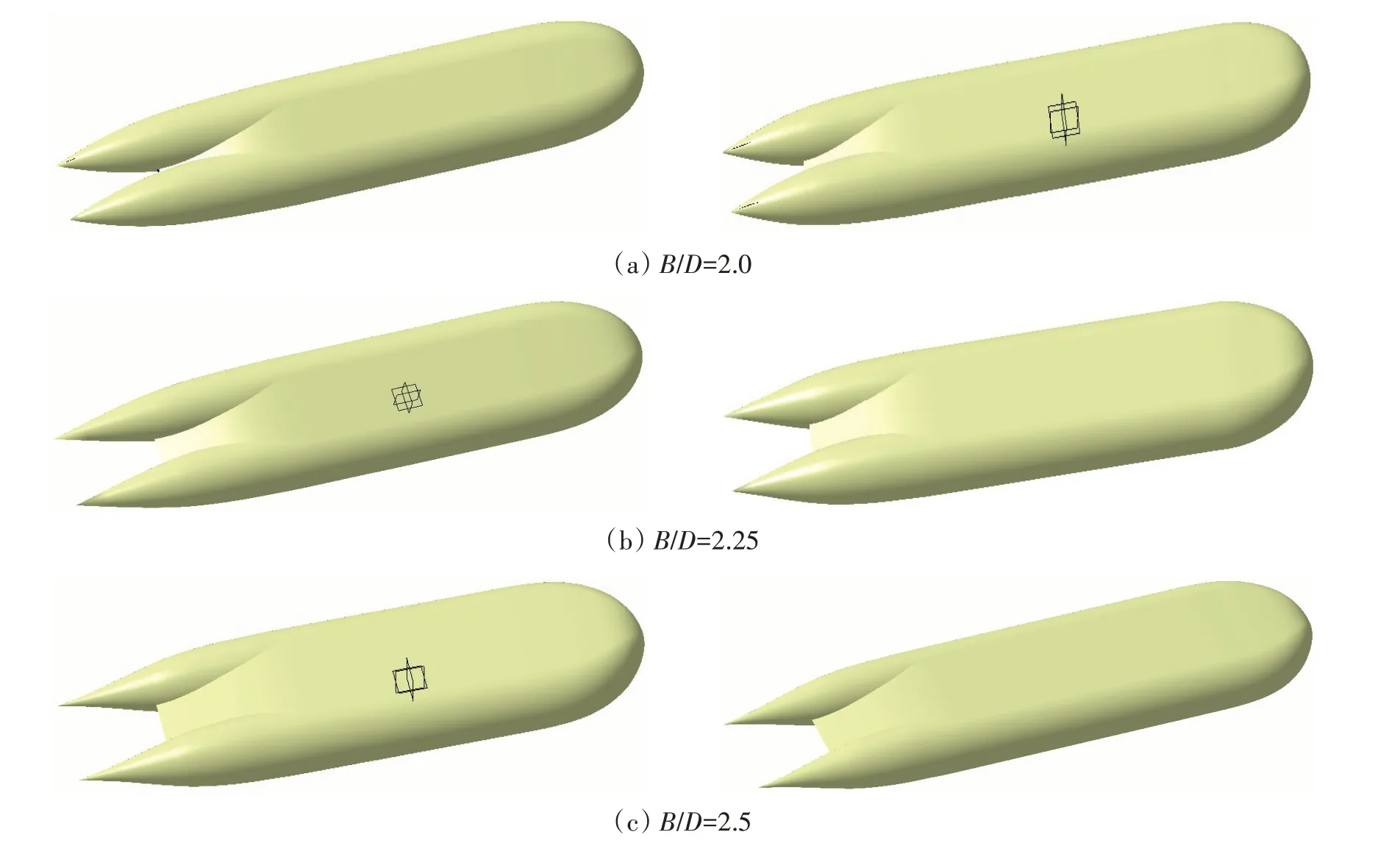
图6 自动生成的不同扁平度参数的三维模型Fig.6 Automatically-generated 3D models with different B/D parameters
2.3.2 自动建模计算验证
为了考核验证自动参数化水动力计算模块程序的正确性、可靠性与高效性,改变艇型型宽B,保持总长Lah=3.174 m、型高D=0.305 mm和其他几何参数不变,取B/D=2.0、2.25和2.5,参数化计算水域建模、网格划分与计算参数设定等,然后进行性能计算。艇型(B/D=2.0)自动建模计算与网格划分如图7所示,可以看出自动生成的计算网格比较合理。自动参数化水动力建模计算结果表明,非回转艇型头部与尾部均出现了压力波动,且头部最大水线方向较中纵剖线方向压力最低点压力更小,且下降得更快,这是由于头部中纵剖线方向曲率半径比最大水线方向曲率半径小,中纵剖线方向流动提前发生转捩。最大水线方向在X/L=0.1 处达到压力最低点,而中纵剖线方向流动在X/L=0.04 处达到压力最低点,计算结果与理论预测情况一致,计算结果如图8~10所示。

图7 计算模型网格生成(B/D=2.0)Fig.7 Mesh generation of the computing model(B/D=2.0)
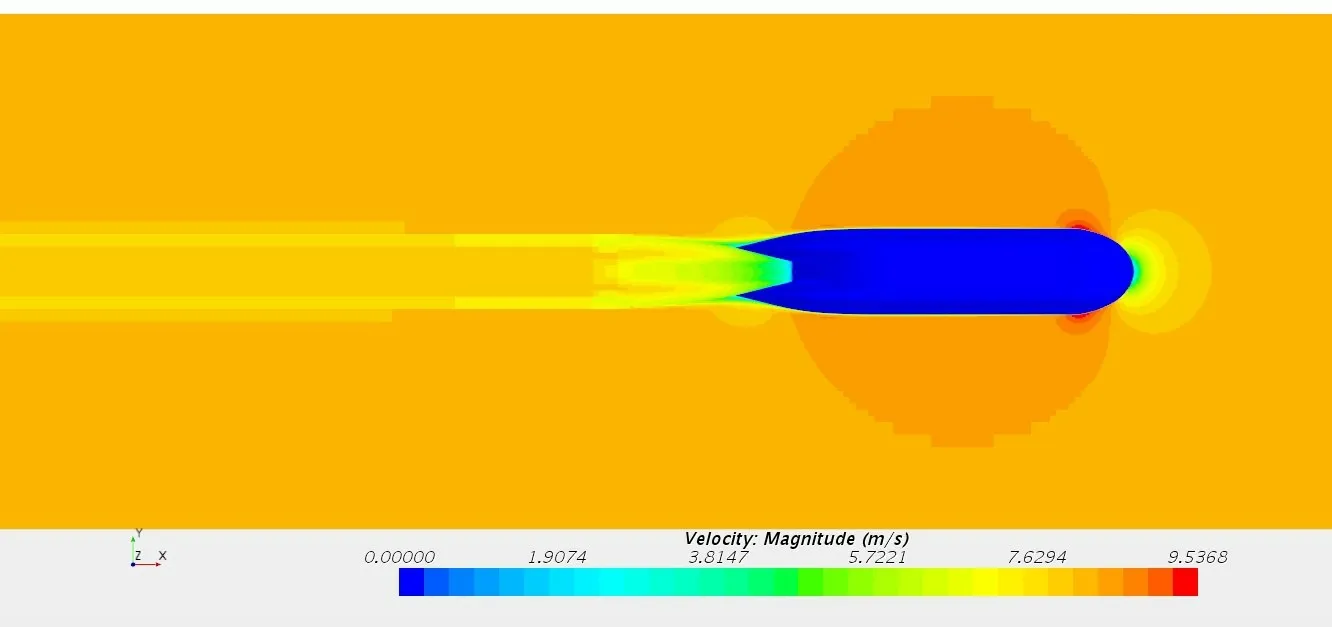
图8 模型计算得到流场速度分布云图Fig.8 Calculated flow velocity distribution

图9 模型计算得到流场压力分布云图Fig.9 Calculated flow pressure distribution

图10 艇型表面最大水线与中纵剖线计算压力分布Fig.10 Calculated flow velocity distribution of maximum waterline and middle longitudinal section line of the hull surface
中国船舶科学研究中心开展了非回转艇型模型拖曳水池水动力性能试验测试[13],如图11所示,试验模型与构型模型外形相近,总长Lah=3.389 m、型宽B=0.767 m、型深D=0.367 m。列出了不同扁平度艇型计算阻力结果,与模型试验结果对比表明,系列参数化快速建模计算与试验测试结果比较接近,说明参数化水动力建模计算模块计算可靠,且计算效率较高,如表2所示。

图11 非回转艇型拖曳水池模型试验Fig.11 Towing tank test of the non-body-of-revolution model

表2 参数化计算与试验结果对比Tab.2 Results of parametric calculation and test
3 结 论
针对非回转水滴艇型复杂三维构型与自动建模计算问题,本文分析了非回转体艇型参数化构型与自动建模计算流程思路,基于不同剖线的船型特征参数,采用数学方程参数化表达剖线型线,对计算水域建模、网格划分与计算输入变量进行了参数化,开发了核心算法与高效自动建模计算程序,搭建了艇型参数化快速构型生成与自动建模计算的程序软件平台,经计算与试验验证了理论与算法程序的正确性。得到的主要结论如下:
(1)本文对非回转体艇型横向、水平向和纵向三个方向分别选取特征参数,并对艇型采用了数学方程进行表达,提出的数学理论方法可用于非回转体艇型快速构型生成。
(2)针对非回转体艇型,完成了艇型生成核心算法、接口程序开发,实现了非回转体艇型的自动生成,可以用于平台艇型设计与优化。自动生成系列不同扁平度参数的三维艇型模型表面光滑、无瑕疵,并能获得相应总体参数,证明了编制算法程序的正确性。
(3)完成了非回转体艇型参数化快速建模计算算法、接口程序开发,实现了参数化计算水域建模、网格划分与计算参数设定等,然后自动进行性能计算,计算与试验结果对比验证了计算模块程序的可靠性。本文工作可为艇型性能优化提供方法,并可大大提高艇型性能计算效率。
