基于特征优选与深度学习的车载电源微小故障诊断方法

2022-12-01李炜韩寅龙孙晓静

兵工学报 2022年11期

李炜，韩寅龙，孙晓静

(1.兰州理工大学电气工程与信息工程学院，甘肃兰州 730050；2.甘肃省工业过程先进控制重点实验室, 甘肃兰州 730050;3.兰州理工大学电气与控制工程国家级实验教学示范中心, 甘肃兰州 730050;4.兰州电源车辆研究所有限公司, 甘肃兰州 730050)

0 引言

随着现代战场信息化程度日益提高，军事装备的电能需求亦快速增长。车载电源以其移动快捷、低噪声运行、操作简便、环境适应性强等技术优势，广泛应用于部队野战照明、指挥、控制、通讯、电子对抗、工程作业及抢险急救等[1-2]。通常车载电源工作环境复杂多变，故障种类多且随机性高[3]。各类微小故障往往是导致系统无法正常工作的源头，运行过程中一旦演变为严重故障，轻则使整个武器系统可能陷入瘫痪，影响军队战斗力，重则甚至造成危及人员生命和财产安全的重大事故。因此，若能及时发现系统常见故障的早期征兆，准确识别出微小故障类型，提前进行防御性维护，则可降低或避免严重故障的发生，提高车载电源安全可靠性。

微小故障具有故障特征不明显、容易被噪声和扰动淹没、不同微小故障之间难以准确区分等特点，因而迫切需要识别能力更强的故障诊断方法。车载电源本身属于复杂的机电系统，由于建模代价高且难以建立精确的数学模型，加之先验知识有限，因此传统基于解析模型、专家知识的诊断方法并不适用于车载电源的微小故障诊断[4-5]。得益于传感器与信息技术的迅速发展，复杂系统可以获得海量、多源、高维的相关监测数据[6]，因而基于数据驱动的智能故障诊断方法已成为解决复杂系统微小故障诊断的重要途径。其中基于神经网络的诊断方法因其具有较强的非线性拟合能力、自学习能力，已被应用于复杂系统微小故障诊断[7-8]。

理论上，只要对监测数据进行合理且足够深度的挖掘，便可以获得数据更为细致化的特征。但是传统的神经网络因自身的浅层结构，限制了其从监测数据中充分挖掘微小故障特征的能力，也就影响了其诊断能力。Hinton等[9]在2006年首次提出了深度学习的思想，并证明了通过深度多层的网络结构自动提取数据的高层次特征，能够更加完整地描述原始数据，这无疑为微小故障诊断的研究开辟了新的途径。Tamilselvan等在文献[10]中给出了一种基于深度置信网络的健康诊断方法，对飞机发动机和电力变压器的健康状态进行有效的诊断。文献[11]提出了一种基于改进的卷积神经网络作为微小故障特征提取器，支持向量机(SVM)代替Softmax作为分类器的方法，用于电机轴承的微小故障智能诊断。为确保高速列车稳定安全运行，文献[12]提出了一种改进的长短时记忆网络自编码器结构，通过从原始信号中提取故障特征，实现了高速列车牵引系统微小故障的无监督诊断。文献[13]提出了一种基于改进卷积神经网络的深度学习算法，用于船舶旋转机械微小故障的快速诊断。

对于微小故障诊断，基于深度学习的故障诊断算法仍存在训练时间长、诊断精度有待提高等问题，除了深度学习参数优化自身的原因外，与数据的特征优选不无关系。因此，针对车载电源这一复杂机电系统微小故障的诊断需求，为了获取更本质的数据特征，提高故障识别准确率，减少时间成本，本文提出一种基于递归特征消除(RFE)和栈式自编码网络(SAE)相融合的微小故障智能诊断方法。首先应用RFE算法对采集到的车载电源运行数据进行特征优选，剔除对分类不敏感的冗余特征，在此基础上采用深度学习中的SAE网络完成车载电源的微小故障诊断，以期达到准确诊断车载电源微小故障的目的，为尽早消除潜在安全隐患提供依据。

1 车载电源微小故障分析

车载电源是一类典型的复杂机电系统，其主要模块包括柴油机、电子调速器、同步发电机、励磁系统。由于各个模块之间具有强耦合性，故障机理较复杂，故障类型既有电气故障，也有机械故障[14]。在长期运行过程中由于负载变化、元部件退化磨损以及环境恶劣等因素，系统会逐渐出现一些故障，如同步发电机失磁、发电机三相电压不平衡、电机匝间短路、喷油嘴堵塞、调速器失效等，上述故障一旦发生将导致车载电源无法正常工作。而车载电源微小故障具有测量信号征兆不明显且噪声大等特点。当微小故障发生时，车载电源可能仍以某种状态继续运行，但是随着时间的推移，微小故障将逐渐演变为严重故障，其本质上是系统相关参数从“量变”到“质变”的过程，引发故障的机理是一致的。因此本文研究车载电源微小故障将聚焦于上述几种常见故障的早期阶段，具体可根据国家军用交流移动电站通用规范(GJB 235A—97)中四类电站指标界定。

故障机理与征兆数据是开展微小故障诊断研究的基础。考虑车载电源前期历史监测数据匮乏，破坏性试验成本过高，而复杂系统虚拟仿真不仅可行而且已是未来发展趋势，在深入分析前述车载电源故障机理的基础上，借助实验室团队前期为军方用户研发的“车载电源仿真系统”，该系统模型与车载电源实体的一致性前期已通过实体对象实验验证。通过在此平台接入辅助元件或调整相关模块参数，分别模拟不同故障工况并采集监测数据，进而依据GJB 235A—97中四类电站的电气性能主要指标，结合行业专家经验与历史数据，最终确定4种车载电源微小故障，如表1所示。

表1 车载电源微小故障

2 基于RFE-SAE的车载电源微小故障诊断方法

2.1 基于RFE-SAE车载电源微小故障诊断方法思想的提出

深度学习具有从原始样本中自动学习数据本质特征的能力，通过构建的深层神经网络可从输入数据中挖掘更具抽象性、细节化的高阶信息，而这些高层次特征无疑是提升微小故障诊断性能的关键因素[4]。SAE作为深度学习领域中的经典网络模型，其通过对输入数据的“复制”逐层提取高阶特征，并在此过程中实现数据降维，将复杂的输入数据转换为更具代表性的低维特征。SAE网络模型的特性完全契合微小故障诊断的目标需求，因此选择SAE用于车载电源微小故障特征的提取，再通过添加一个Softmax分类器，对于车载电源常见微小故障的诊断无疑是可行的。

考虑到实际中用于车载电源状态监测的数据较多，测量数据中的变量对于微小故障，其敏感度各有差异，且存在一定的冗余。为提高SAE无监督学习效率与微小故障诊断能力，需先对原始测量数据进行特征选择。RFE算法通常被用于消除冗余和无用特征，应用领域较广泛。相对于经典的特征降维方法——主成分分析，通过RFE选择最优特征子集时，不仅可以将特征变量按其对故障分类的重要度排序，为剔除冗余特征提供依据，而且构造的新特征子集还可保持原始测量数据的可解释性。因此将RFE作为车载电源微小故障测量数据特征变量的优选算法，更利于故障溯源。

本文在SAE网络基础上引入RFE算法，以实现车载电源微小故障的快速有效诊断。基于RFE-SAE车载电源微小故障诊断算法，主要包括特征优选、微小故障特征提取和故障模式分类等三部分。该算法的核心思想是：对于大量监测数据构成的特征集，首先利用RFE算法对特征进行优选，剔除对微小故障分类不敏感的冗余特征；其次在此基础上利用无标签样本无监督地训练SAE，进一步挖掘故障的深层特征；最后结合分类器有监督的对整个网络模型参数进行反向微调，从而使整个深度网络可以更好的在优选特征子集中提取微小故障特征，并进行微小故障模式的有效分类。

2.2 基于RFE的车载电源微小故障特征优选

RFE算法本质是根据原始数据对分类器性能指标的重要度来评价特征，并通过重要度产生特征排序，其性能与采用何种迭代分类器有关，常用的分类器有SVM、随机森林、朴素贝叶斯等。基于SVM的递归特征消除(SVM-RFE)是由Guyon等[26]在2002年进行癌症分类的基因选择时提出来的。SVM-RFE作为经典的封装器模型算法，其中SVM作为分类器，在每一轮训练时会选择所有特征值进行训练，根据特征排序准则，在每次迭代训练时去掉一个排序系数最小的特征变量，最终得到所有特征重要性的递减顺序的排序。

本文采用SVM-RFE算法对车载电源候选特征进行重要度排序，目的是从中选择出对常见微小故障更为敏感的最优特征子集，以其作为深度学习网络的输入。候选特征集由车载电源监测数据中的15种相关变量构成，具体包括有功功率P、无功功率Q、功率因数cosφ、频率f、转子转速n、电磁转矩Te、定子电压Us、定子电流Is、励磁电压Ef、三相电压UA、UB、UC以及三相电流IA、IB、IC。构建车载电源微小故障候选特征向量集合X∈RN×M，故障特征标签集合y∈R。

(1)

(2)

式中：N表示特征集合中样本个数；M表示候选的特征变量个数，即M=15；k表示车载电源工况类型对应的标签,由表1常见微小故障类型加上正常状态共计k=5。

基于SVM-RFE的车载电源特征优选，是利用候选特征集中的样本训练SVM，并通过特征排序系数公式(3)式计算各个特征权重，作为特征排序的依据。目标分类器SVM采用径向基核函数代替内积，如(4)式所示。

(3)

(4)

式中：r为特征序号；α为拉格朗日乘子；H为样本矩阵，H(-r)表示第r个特征被移除时矩阵的值；Hij表示核函数K(xi,xj)对应的核矩阵，xi，xj为输入样本；σ表示高斯核的带宽。基于SVM-RFE算法流程如图1所示。

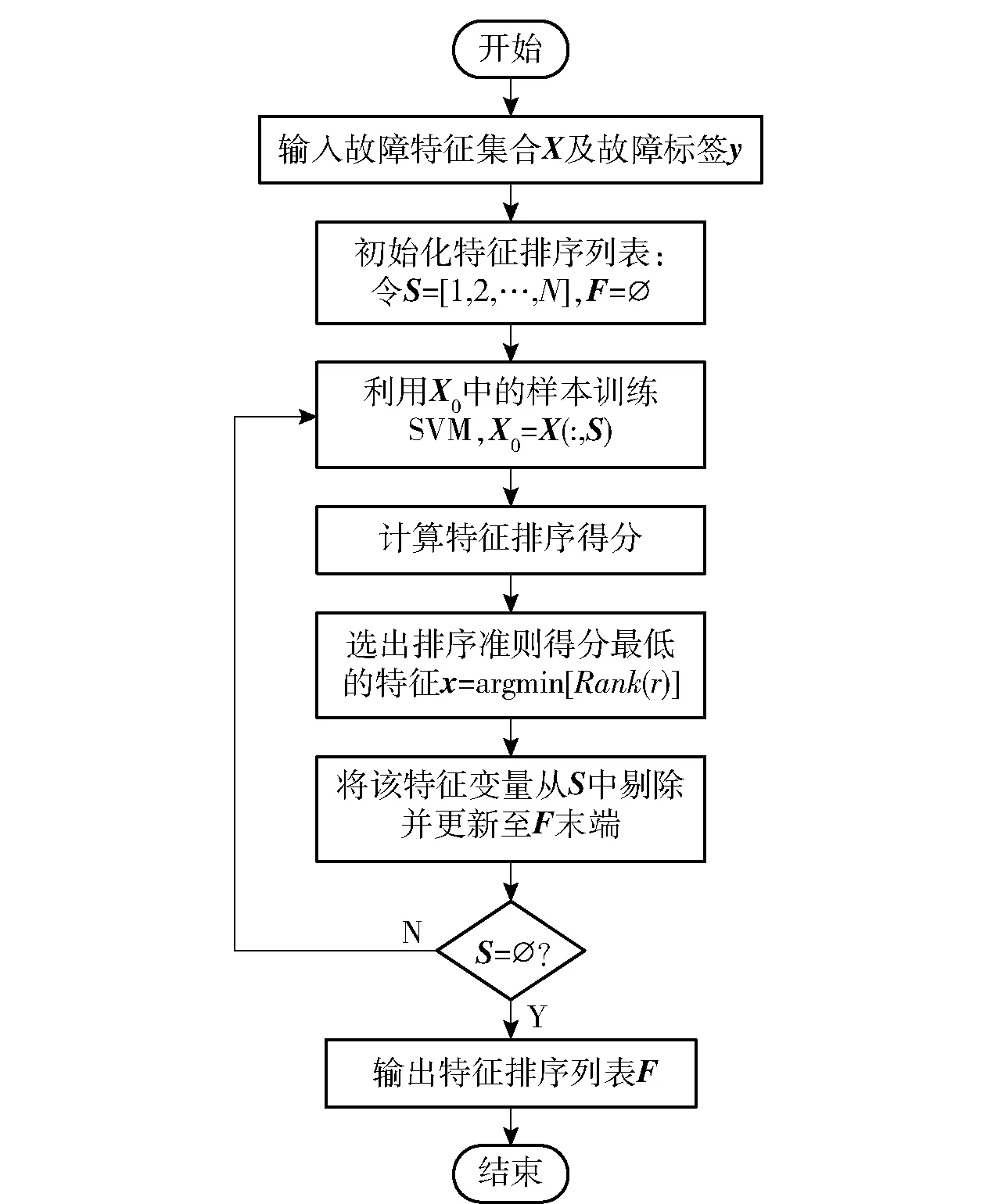
图1 SVM-RFE算法流程图

图1中，S表示当前候选特征排序列表，F表示最终输出的特征排序列表；二者在每次执行完毕后进行更新；∅表示空集。

2.3 基于SAE的车载电源微小故障诊断

自编码器(AE)主要包括编码器和解码器两部分。其中编码器由输入层和隐层组成，其对原始数据进行编码，在隐层得到特征向量并“压缩”原始数据。解码器由隐层和输出层组成，隐层输出的特征向量通过解码器“还原”为原始数据，当输出数据和原始数据之间的重构误差足够小时，则认为隐层输出的高阶特征可以有效表达原始数据[27-28]。多个自编码网络堆叠在一起构成了SAE，其能够获取比原始AE网络更抽象的特征表达。SAE因利用“贪婪逐层”算法训练网络，解决了传统神经网络算法容易陷入局部最优的问题[29-30]。因而其与原始的自编码网络相比，更适合复杂的多分类问题。

单层AE网络编码过程可定义为

h=sf(Wx+b)

(5)

式中：h为隐层输出的特征集合；sf(·)为编码器的激活函数，一般选择sigmoid函数；W为输入层到隐层之间的权值矩阵；x为原始输入数据；b为输入层到隐层之间的偏置矩阵。

解码过程可以定义为

x′=sg(W′h+b′)

(6)

式中：x′为输出集合；sg(·)为解码器的激活函数；W′为隐层到输出层之间的权值矩阵；b′为隐层到输出层之间的偏置矩阵。

自编码器通过寻求最优参数{W,W′,b,b′}令输出x′尽可能的还原输入x。网络输出层采用非线性激活函数，其还原程度用重构误差来定义，即

(7)

式中：m为样本数。

车载电源微小故障诊断的深度网络模型中使用多层堆叠的AE来提取更高级别的微小故障特征。对SAE执行分层的正向无监督训练，随机初始化第1层 AE的初始权值和偏置{W1,W′1,b1,b′1}，采用(7)式所示的均方误差作为损失函数，通过梯度下降算法训练网络使得重构误差达到最小。待第1层AE网络训练完成后只保留其编码部分，然后将第1层 AE提取的高级特征作为第2层AE的输入，并对第2层网络进行训练。以此类推，完成整个网络的训练后，最后一层网络输出的高级特征即为车载电源微小故障最终的特征表达。

将一个Softmax分类层连接在SAE网络层顶端，使用样本标签和提取的微小故障特征进一步训练整个深度网络，微调网络参数。同时Softmax分类层输出车载电源各类微小故障的概率，最终完成故障诊断。SAE网络结构可表示如图2所示，其输入为车载电源最优特征子集，输出为微小故障类别标签。

图2 SAE网络结构图

2.4 基于RFE-SAE车载电源微小故障诊断框架与步骤

综合2.1节～2.3节，基于RFE-SAE的车载电源微小故障诊断方法框架如图3所示。

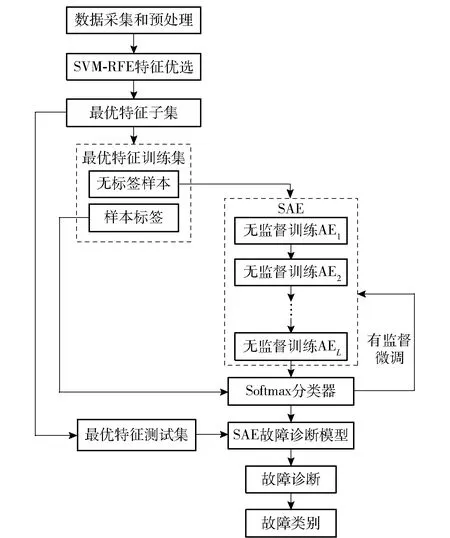
图3 车载电源微小故障诊断框架图

本文所提车载电源微小故障诊断方法其诊断步骤如下：

步骤1在车载电源仿真平台模拟表1内对应的微小故障，并采集运行数据。

步骤2对采集到的数据进行归一化预处理，消除不同特征之间的量纲影响。

步骤3利用SVM-RFE算法对候选特征集进行特征重要度排序，并通过优选得到最优特征子集。

步骤4将最优特征子集按一定比例随机生成训练集和测试集。

步骤5初始化网络参数，即设置SAE网络的网络层数和每层单元数，并随机初始化其权值和偏置。

步骤6将训练集中无标签样本输入上述多层网络，采用逐层贪婪的方法对网络进行训练，提取故障特征并更新网络参数。

步骤7在SAE网络顶部添加Softmax分类器，将提取到的特征和样本标签作为分类器的输入，通过误差反向传播算法，对整个网络的参数进行有监督的微调。

步骤8将测试集输入已建立的SAE故障诊断模型，进行故障分类。

3 仿真实验与结果分析

3.1 数据采集与评价指标

本文通过车载电源仿真平台分别模拟5类运行工况，即系统正常运行、同步发电机部分失磁、同步发电机三相电压不平衡度1%～2%、喷油嘴轻微堵塞、调速器退化。采集相应的运行数据构成候选特征集，数据集中每类工况包含5 000个样本，共计 25 000个数据，具体数据集描述如表2所示。在数据集中随机抽取80%的样本作为训练集，即20 000个样本用于网络模型的训练。剩余20%的样本作为测试集，即5 000个样本用于模型最终的微小故障诊断效果测试。

表2 车载电源微小故障数据集描述

为了客观量化的评价所建模型对车载电源常见微小故障诊断的有效性，考虑其本质仍属于多分类问题，在此运用分类任务中常用的评价指标：准确率(accuracy)、精度(precision)、召回率(recall)，对RFE-SAE诊断模型进行评价。计算第i类样本的评价指标时，将第i类作为正类，其他类作为负类。评价指标计算公式如下：

(8)

(9)

(10)

式中：TP表示模型输出为正类且实际为正类的样本数量；TN表示模型输出为负类且实际为负类的样本数量；FP表示模型输出为正类且实际为负类的样本数量；FN表示模型输出为负类且实际为正类的样本数量。

3.2 基于RFE的特征优选结果分析

在完成数据采集工作后，首先采用MAX-MIN归一化算法对不同特征进行预处理。进一步为了消除冗余特征，根据2.2节中SVM-RFE算法步骤对15个候选特征变量进行重要度排序，重要度排序结果如表3所示。

表3 基于RFE的特征重要度排序

考虑到特征个数在一定程度上会影响到网络模型的性能，过少选择特征个数会丢失有用的故障信息，降低故障诊断效果。为了选择出车载电源微小故障诊断模型最适用的优选特征子集，按表3第2行中的排序，从重要度排序最低的特征变量开始，逐次递增变量个数进行剔除，将剩余特征变量作为模型输入。预先设定SAE网络隐层结构为2层AE组成，每层分别取9个和6个神经元，在此模型结构下进行试验，最终得到特征变量剔除个数不同时微小故障诊断准确率的结果，如表4所示。

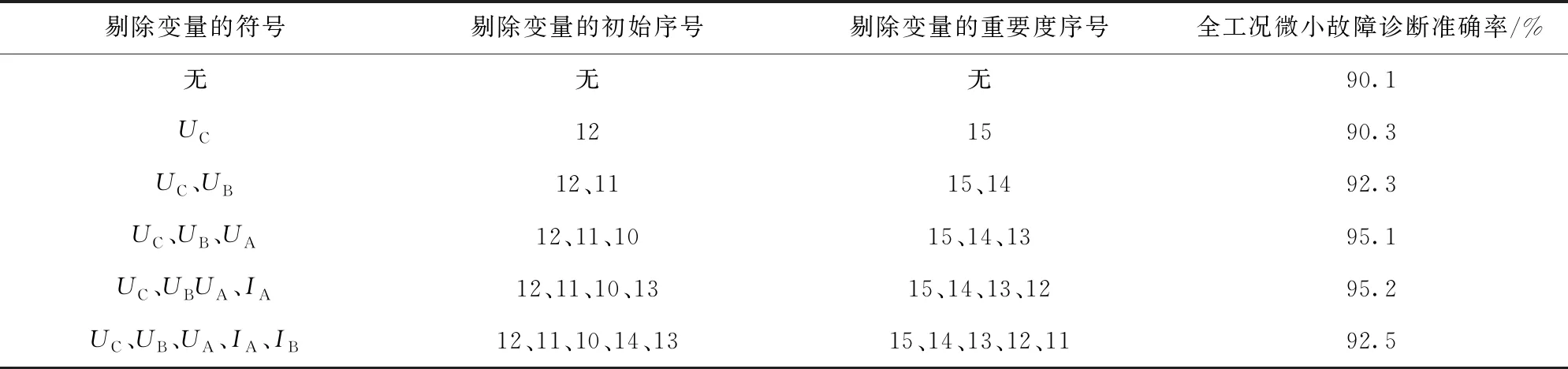
表4 特征剔除个数与故障诊断结果的关系

由表4可以看出：从输入全部15个特征变量开始，逐步剔除1～4个重要度低的冗余特征，SAE模型对微小故障的诊断准确率随之提高；当剔除4个重要度排序最低的特征变量时，故障诊断准确率达到最高，为95.2%。进一步剔除特征变量故障诊断准确率反而下降。表明对故障分类非关键特征量过多地保留以及对其过度剔除，均会降低SAE网络对微小故障的诊断性能，前者因为冗余使网络鲁棒性变弱，后者则因丢失过多有用的信息致使网络诊断能力降低。

综上结果文中选取重要度排序前11的特征变量作为优选后的微小故障特征数据集，即SAE网络模型的输入。

3.3 SAE网络结构及参数的确定

为了确定SAE网络模型结构，对深度网络的隐层数量和隐层神经元个数进行优化实验。根据前期大量仿真经验，综合考虑后对SAE隐层数和隐层神经元数量设置一个试验范围，其中隐层数由2层递增到4层，隐层神经元数量范围为5～10个。选用Sigmoid函数作为隐层的激活函数，代价函数选用均方差损失函数，网络迭代次数为2 000次。以全工况下的微小故障诊断准确率作为优化试验的评价指标，确定此模型最优的SAE网络结构，具体结果如表5所示。

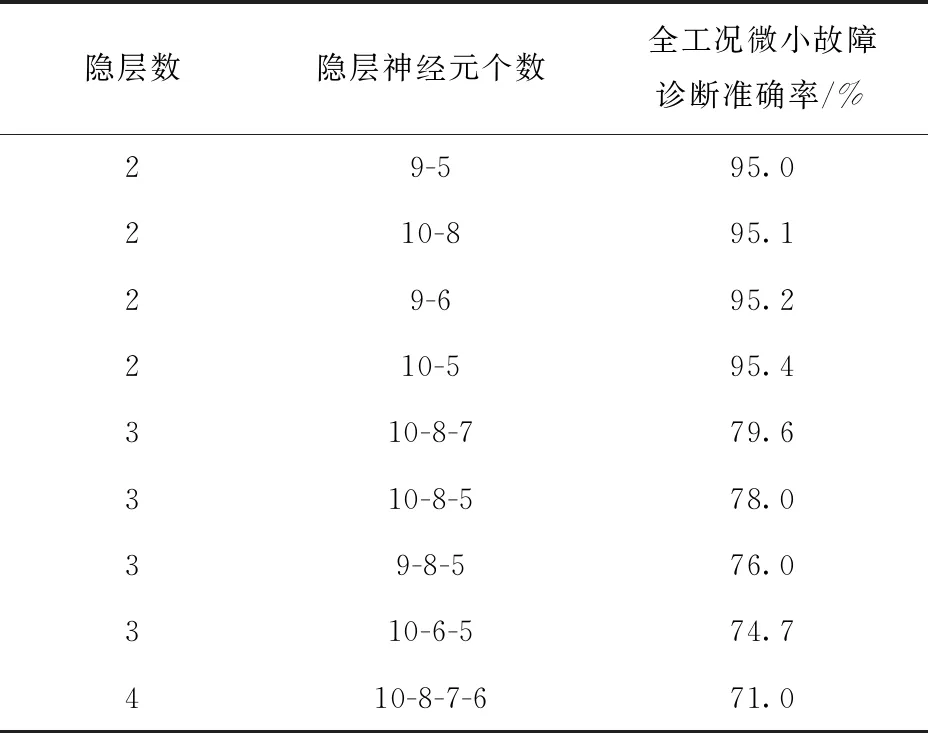
表5 SAE网络隐层数量及隐层神经元个数对于故障诊断结果的影响

表5给出了9种组合下SAE网络模型的微小故障诊断准确率。对于2层隐层中的[10 5]组合，其准确率最高，为95.4%，表明该结构最利于SAE网络学习车载电源微小故障的数据特征。对于3层、4层隐层的5种组合虽然增加了网络隐层数量和隐层神经元个数，但是其准确率并不理想，反而会增加网络训练时间。综上，最终确定SAE整体网络结构为4层，其中隐层为2层AE，神经元个数分别为10-5。输入层神经元个数对应车载电源优选特征集中变量个数，即11个。Softmax分类层作为输出层，其神经元个数对应表1中车载电源5类工况(正常与4类微小故障工况)。

3.4 基于RFE-SAE的故障诊断结果分析

混淆矩阵可以较为直观全面的反映车载电源不同微小故障的诊断准确率和召回率，以及各类微小故障误诊、漏诊的样本数量。因此将RFE-SAE模型的微小故障诊断结果使用混淆矩阵进行可视化，如图4所示。其中横轴坐标表示故障诊断的目标类别，纵轴坐标表示模型输出的故障类别，主对角线右下角单元格显示全工况的故障诊断准确率为95.4%。矩阵第1行表示第1种工况下有866个样本被正确诊断，88个样本被误诊，诊断精度达到90.8%，错误诊断率为9.2%。矩阵第1列表示第1种工况中共有101个样本被漏诊，召回率为89.6%，其漏诊率为10.4%。

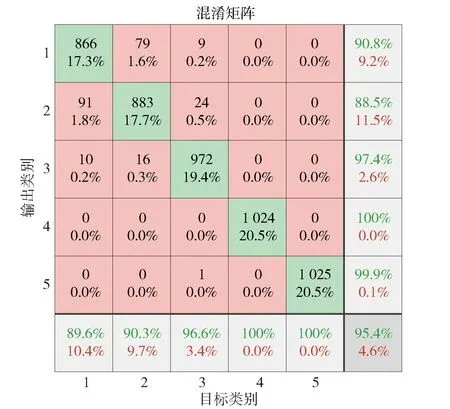
图4 RFE-SAE模型故障诊断结果

为了显示本文方法对车载电源微小故障的优势，仿真实验同时对基于浅层BP神经网络，RFE-BP网络以及单纯SAE网络3种模型分别进行了测试。不同模型诊断结果的混淆矩阵如图5所示。

图5 不同模型故障诊断结果

图5(a)～图5(c)分别显示出BP、RFE-BP、SAE 3种模型在全工况下的故障诊断准确率分别为78.2%、82.1%、93.1%，均低于图4中RFE-SAE模型的95.4%。考虑到各个模型训练过程中的偶然性和随机因素对诊断结果的影响，为了使故障诊断结果更具说服力。对4种网络模型各进行10次故障诊断试验并对诊断结果进行统计，求取不同模型诊断结果的准确率、精度、召回率3项评价指标的平均值，具体统计数据如表6所示。

从表6中的对比数据可以看出：仅就全工况下的故障诊断准确率而言，基于RFE-SAE的网络模型诊断效果最好，其总体故障诊断准确率的平均值达到95.4%，较SAE网络故障诊断准确率提高了2.4%；RFE-BP将BP的故障诊断准确率平均值从78.1%提升到81.5%，但诊断效果仍不理想。上述结果充分表明：对于微小故障诊断，深层网络明显优于浅层网络，尤其是文中提出的RFE-SAE模型具有更强的故障诊断能力，因此更加适合应用于车载电源的微小故障诊断。

表6 不同模型诊断效果对比结果

为了进一步说明RFE-SAE网络模型的优势，在仿真过程中分别统计了各模型训练与测试计算时间，仿真实验环境基于16G内存的i7-8750H处理器笔记本电脑。不同模型网络耗时如表7所示。

表7 不同模型训练计算时间

对比表7中各模型训练时长可知，BP神经网络因其自身的浅层结构所以训练耗时较短，深度网络SAE模型耗时最长。在引入RFE算法后，RFE-BP模型对比BP网络的训练时长缩短了3.74 s，RFE-SAE模型训练时长为83.071 8 s，相对于SAE网络模型训练诊断耗时缩短14.7%，表明特征优选可以有效减少网络训练耗时，提升模型故障诊断效能。