气淬高炉渣颗粒凝固行为数值模拟
2022-12-01王丽丽客海滨王立梅
王丽丽,客海滨,王立梅
(1.唐山学院 a.机电工程学院,b.河北省智能装备数字化设计及过程仿真重点实验室,河北 唐山 063000;2.河钢唐钢集团 炼铁事业部,河北 唐山 063016)
0 引言
对于高炉渣的处理,气淬粒化法是最有希望代替传统水淬粒化法的一种干法粒化工艺,具有余热高效回收、不产生环境污染、不消耗水资源、工艺简单、运行稳定、处理能力强等优点[1-2]。气淬粒化法包括粒化和传热两个过程。粒化后的炉渣颗粒在空气中飞行并因与空气进行热量交换而凝固,高炉渣的凝固行为对于提高渣粒玻璃相率、高效回收空气余热及合理设计余热系统至关重要。
Sun等和邱勇军等[3-4]利用Fluent软件模拟得到了高炉渣颗粒内部的温度分布,讨论了颗粒直径和冷却风速对温度分布的影响。Zhu和Ding等[5-6]结合影响因素的分析结果,提出了5 mm高炉渣颗粒的最佳冷却条件。刘小英等[7]提出了一种基于焓值法的传热模型,表明较小的颗粒直径和较快的空气流速有利于高炉渣颗粒缩短凝固时间。Gao等[8]采用焓法,建立了描述高炉渣颗粒结晶行为的二维对称模型,揭示了局部冷却速率和晶相含量分布的演变过程。米沙等[9]对空气绕流高温冶金熔渣颗粒进行了非稳态三维数值模拟,研究了熔渣颗粒与空气的换热性能以及熔渣所受的空气阻力特性。
基于前人的研究,本文采用凝固熔化模型(Solidification/Melting Model)、流体体积函数模型(VOF模型)和离散坐标辐射模型(DO模型)对高炉渣颗粒的凝固换热进行三维瞬态模拟,以分析颗粒的凝固行为,从而为提高渣粒品质、余热高效回收以及后续的工业应用提供理论指导。
1 数值模拟
1.1 物理模型及模拟方法
将高炉渣与空气的换热环境设计成一个正方体物理模型(如图1所示),其边长为10 mm;将高炉渣颗粒视为球体,位于正方体中心,颗粒直径为2 mm,空气由左侧进入、右侧流出。左侧入口为速度入口,空气入口速度为15 m·s-1,右侧出口为压力出口,其他表面均为wall。

图1 高炉渣颗粒换热环境物理模型
采用凝固熔化模型和离散坐标辐射模型求解空气和颗粒的换热问题。采用流体体积函数模型解决颗粒内部固液两相界面的移动问题。对颗粒凝固行为进行三维瞬态模拟,空气入口温度为300 K,高炉渣的固相线温度为1 651 K,液相线温度为1 671 K[10]。
1.2 控制方程
凝固熔化模型能量方程为:
(1)
式中,t为时间,s;ρ为密度,kg·m-3;H为物质的焓,J;u为流体速度,m·s-1;k为导热系数,W·m-1·K-1;T为温度,K;S为源项。
DO模型辐射能的计算式为:
E=εσ0A(T14-T24)。
(2)
式中,E为辐射能,J;ε为黑度;σ0为黑体辐射常数(σ0=5.67×10-8W·m-2·K-4);A为表面积,m2;T1为高温表面温度,K;T2为低温表面温度,K。
VOF方程为:
(3)
式中,αq为液相体积分数。
1.3 物性参数
固相区高炉渣比热cps为1.15 kJ·kg-1·K-1,液相区高炉渣比热cpl为1.30 kJ·kg-1·K-1,模糊区高炉渣比热cpls按其液相百分含量计算,如式(4)所示:
cpls=cplβ+cps(1-β)。
(4)
式中,β为液相百分含量。
高炉渣导热系数随温度变化,可变导热系数为[3]:
ks=
(5)
假设空气物性参数不随温度变化。空气的物性参数见表1。

表1 空气物性参数
2 模拟结果与分析
2.1 凝固过程
高炉渣颗粒在凝固过程中,温度仅在气流方向(X轴方向)上变化,简化为X轴向一维传热。以颗粒球体中心最大纵剖面为例,凝固过程中不同时刻的固液相分布如图2所示,其中外部为固相区、内部为液相区、中间为模糊区。0.2 s时颗粒迎风面已经凝固成一定厚度的固相,此时背风面两侧上半圆弧和下半圆弧区域均未凝固成固相;0.3 s时颗粒表面已形成了完整的固相硬壳,但硬壳厚度并不均匀,其迎风面固相厚度比背风面大。在竖直方向(Y轴方向)上,固相厚度向上和向下均逐渐减少。随着时间的延长,整个颗粒由外向内固相逐渐增多、液相逐渐减少,1.08 s时全部为固相,达到全部凝固。

图2 不同时刻高炉渣颗粒纵剖面固液相分布
2.2 相界面移动速度
随着时间的延长,固相区-模糊区界面及模糊区-液相区界面均向颗粒内部移动,其移动速度如图3所示。
随着时间的延长,固相区-模糊区界面及模糊区-液相区界面的移动速度均先增加后降低,在0.8 s时达到最大。这是由于液相导热系数(0.1~0.3 W·m-1·K-1)小于固相导热系数(1~3 W·m-1·K-1),随着液相的减少、固相的增多,颗粒内导热系数增大,传热量增加,因此0.8 s之前固相区-模糊区界面及模糊区-液相区界面的移动速度均增加。另外,随着固相的增多,导热热阻变大,固相厚度在0.8 s时已经达到0.73 mm,产生了较大的导热热阻,使内部热量不容易向外传递,因此0.8 s之后模糊区-液相区界面及固相区-模糊区界面的移动速度均有所降低。这说明0.8 s之前导热系数的影响占主导地位,0.8 s之后导热热阻的影响占主导地位。0.6 s之前模糊区-液相区界面移动速度大于固相区-模糊区界面移动速度,说明0.6 s前液相冷却速度快;0.6 s之后,由于导热热阻的增大及相变潜热的释放,液相冷却速度相对变慢,因此模糊区-液相区界面移动速度小于固相区-模糊区界面移动速度。
2.3 颗粒表面及内部温度分布
颗粒表面温度监测点的分布如图4(a)所示,各监测点温度随时间的变化如图4(b)所示。由图4可知,颗粒迎风面A点温度最低,沿AD弧线温度逐渐升高,D点温度最高。A点温度最低,与气体热交换最强,凝固快,固相厚度大;而D点凝固慢,固相厚度小。固相厚度沿AD弧线向上逐渐变小。在背风面DG弧线上,E点温度最高,G点温度最低,D点与F点两点温度相差不大。E点与气体热交换最差,最晚形成固相。在颗粒整个凝固过程中,每个点的温度均随时间的延长而降低。由温度-时间曲线的斜率可知,迎风面各点的斜率大于背风面各点的斜率,说明迎风面温度降低幅度明显大于背风面,即迎风面凝固速度快,因此迎风面固相厚度大于背风面。
颗粒从表面至内部径向温度的分布如图5所示,其中,r1为颗粒内部点到中心的距离,r为颗粒的半径,r1/r=0为颗粒中心,r1/r=1为颗粒外表面。
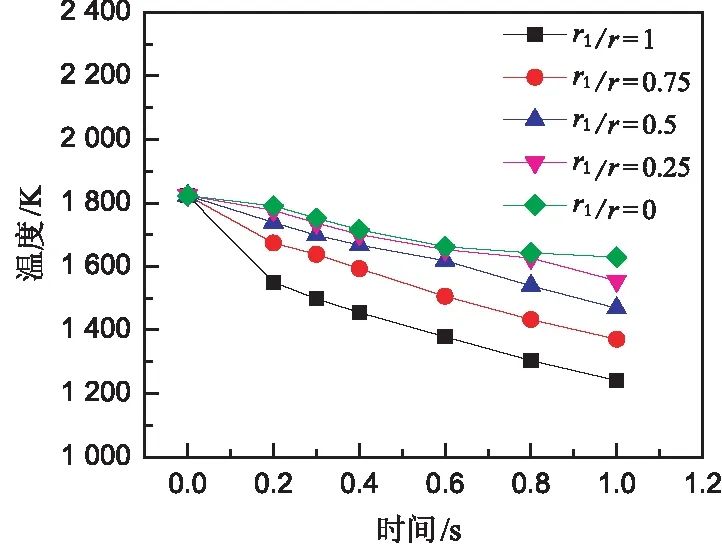
图5 颗粒径向温度分布
同一时刻颗粒表面温度最低、中心温度最高,由外向内温度逐渐升高。颗粒内部径向各位置的温度随时间的延长逐渐降低。r1/r≥0.75,即靠近表面的位置,0.2 s之前温度降低剧烈,这是由于开始时空气与颗粒表面温差较大,换热剧烈,温度降低幅度大。0.2 s之后,温度-时间曲线斜率减小,温度降低幅度变小,这是由于随着时间的延长,空气与颗粒表面的温差逐渐减小,换热相对变弱。r1/r≤0.5,即靠近中心的位置,温度逐渐降低,且越接近颗粒中心温度降低越缓慢。这主要有两方面原因:一是颗粒凝固由外向内不断推进,凝固过程中释放的相变潜热导致颗粒内部温度降低变缓;二是固相区逐渐增厚,冷却介质空气与液态熔渣之间的热阻增大,使内部温度不能及时向外释放,因此,颗粒内部温度降低平缓。颗粒内部温度一直明显高于表面温度,且随着时间的延长,颗粒表面与颗粒中心的温差越来越大。无论是表面温度还是内部温度均未出现温度回升现象,这说明熔渣冷却并未出现液态金属冷却时所表现的再辉现象。
2.4 颗粒周围空气速度分布
颗粒周围空气速度分布(如图6所示)存在明显差异,导致颗粒与周围空气传热的不均匀性。空气速度低或边界层较厚的区域,表面传热系数低,颗粒表面凝固慢。颗粒迎风面的空气速度高于背风面,因此颗粒迎风面传热条件好,凝固快,固相厚度高于背风面。颗粒迎风面中心点的边界层薄,传热效果好,所以颗粒迎风面中心固相最厚;在颗粒竖直方向空气向上和向下流动,虽然其流速增加,但界面层逐渐变厚,使得传热系数降低,所以在竖直方向上向上和向下两侧凝固变慢,固相厚度逐渐变小。在颗粒竖直方向上下两个顶部会出现流动脱体现象,随后在背风面气流速度降低,压力升高,空气出现不稳定的回流,颗粒的背风面在回流区的扰动作用下进行冷却。背风面中心位置空气回流速度大,在竖直方向向上和向下两侧回流速度减小,换热效果差,因此颗粒背风面两侧位置冷却最慢,形成固相最晚,且固相最薄。
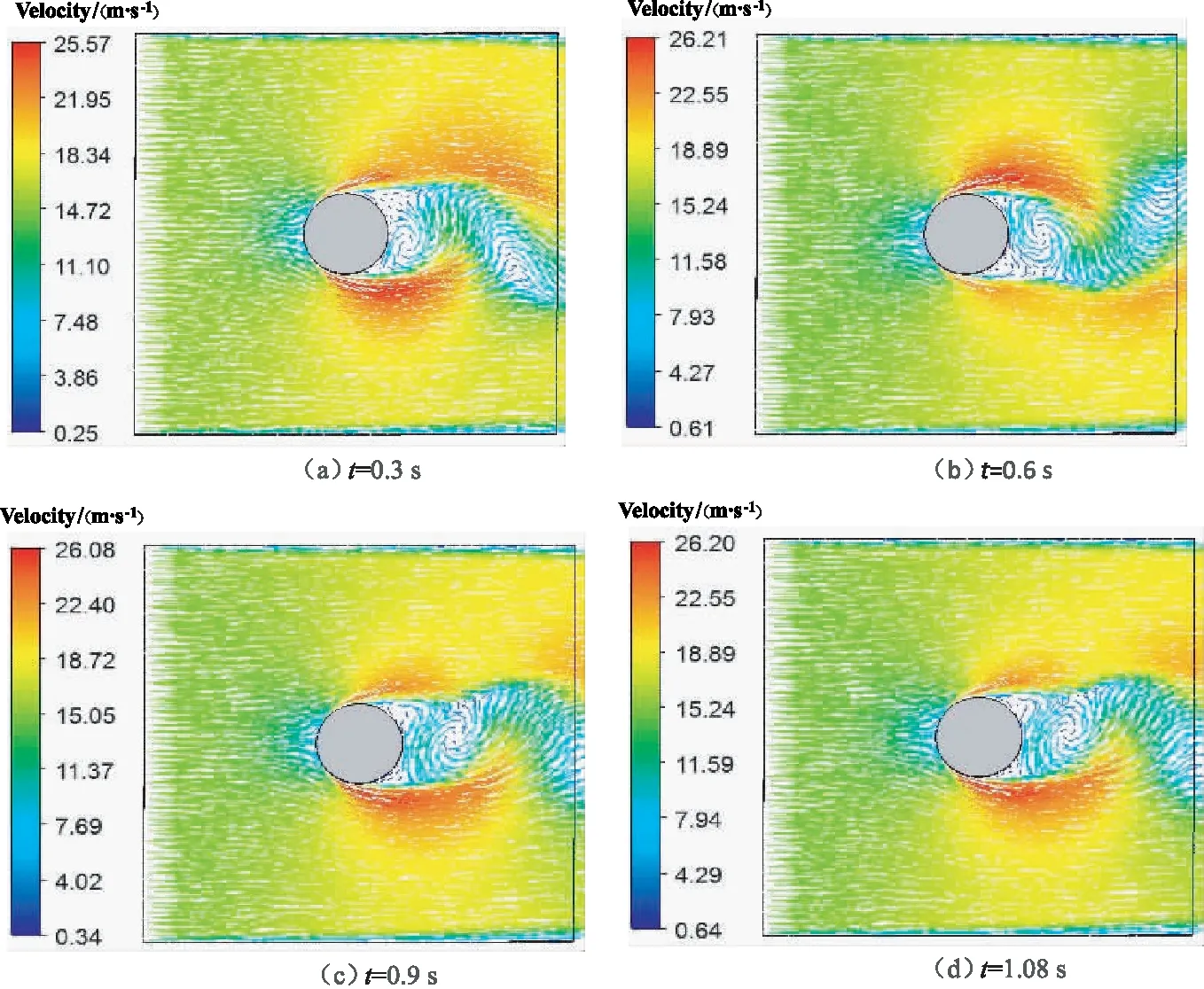
图6 颗粒周围空气速度分布
3 结论
(1)在高炉渣颗粒凝固过程中,固相厚度分布不均匀,迎风面固相厚度大于背风面,竖直方向上中心固相厚度最大,沿上下两侧固相厚度逐渐减小。
(2)凝固过程中,颗粒相界面移动速度先增加后降低,这是由于颗粒在凝固前期导热系数的影响占主导地位,在凝固后期导热热阻的影响占主导地位。
(3)在颗粒背风面空气出现不稳定的回流,背风面在回流区的扰动作用下进行冷却。
(4)颗粒表面温度明显低于内部,且表面温度降低幅度高于内部。
