一种新型泡点压力预测模型的建立和应用<br/>——以塔里木油区为例

一种新型泡点压力预测模型的建立和应用
——以塔里木油区为例

2022-12-01王佳营赵仁保李姝璇齐双瑜

油气藏评价与开发 2022年6期

王佳营，赵仁保，李姝璇，贾瑜，付宁，齐双瑜

（1.中国石油大学（北京），北京 102249；2.西南石油大学，四川成都 610500；3.中国石油川庆钻探工程有限公司长庆井下技术作业公司，陕西西安 710018；4.中国石油大港油田公司勘探开发研究院，天津 300280）

塔里木盆地是一个纵向叠加、横向复合、物性多样，历经多期演化而形成的深层叠合盆地[1]。依据盆地基底顶面起伏特征，将塔里木盆地划分为“三隆四坳”7个一级构造单元，即塔北隆起、塔中隆起、塔南隆起、库车坳陷、北部坳陷、塔西南坳陷和塔东南坳陷。在塔里木盆地的地质演化史中发育了6套区域地层。

塔里木盆地地层原油样品分析统计结果显示，该地区油藏流体气油比从3 m3/m3到720 m3/m3不等，原油相对密度从0.77到1.02不等，根据该地区油藏流体高压物性特征，在确定影响泡点压力因素的基础上，研究了以往经验公式对于塔里木油区的适用性，在此基础上采用塔里木油区现有的样品数据，拟合出复杂地质状况下考虑多因素的一种新的泡点压力[2]经验模型。

目前主要通过2种方法获得泡点压力值：实验室测定法及经验公式法。实验室测定法测试流程复杂，且测试价格昂贵；而经验公式法中不同的经验公式具有不同的适用范围，并且都有其局限性[3]。塔里木油区自1990年至今已分析油藏地层流体PVT样品约700支，涵盖全探区新、老油气区块。随着勘探开发工作不断开展，油藏领域不断扩大，油藏流体的特殊性和复杂性日益突出，其泡点压力的确定也受到越来越多因素的影响，完全采用现场取样的实验测试方法既存在较大的工程风险，又耗费高额的经济成本[4]。因此，研究塔里木油区油藏流体泡点压力的影响因素，并找出快速预测油藏流体泡点压力的模型，对于塔里木油区深层复杂性油藏的研究工作具有重要意义和理论指导作用。以塔里木油区为例，基于132个地层流体样品高压物性数据，利用数模软件对泡点压力进行非线性回归分析，拟合得到适用于塔里木油区的泡点压力预测模型，为油田科研生产应用提供理论分析方法。

1 泡点压力经验公式适用性分析

1.1 已有经验公式的局限性

自1947年STANDING发表利用实际生产数据计算地层原油泡点压力的相关经验公式以来，相关经验公式层出不穷，迄今多达数十种[5-7]。在大量文献调研的基础上，对使用最多、最广泛的5个常规经验公式及其影响因素、公式形式和适用范围进行调研总结，对以下5个常用经验式进行简单介绍（表1），并给出已有PVT高压物性[8]预测的经验公式适用范围统计结果。

表1 常规经验公式Table 1 List of conventional empirical formulas

表2中给出经验公式适用样品流体性质差异，工区流体特性愈接近某个经验公式的适用范围，该公式在理论上计算本工区流体PVT性质时就愈精确[9]。但从表2中塔里木油区的PVT流体性质范围可以看出，各经验公式的适用范围与该工区流体性质相关参数范围相差较大。

表2 经验公式及塔里木油区关键参数取值范围Table 2 Key parameters of previous empirical formulas and application in Tarim Oildom

1.2 经验公式拟合分析

根据塔里木油田的生产数据，对上述5个常用的经验公式做了塔里木油区适用性分析。分析比较相对误差平均值，定义泡点压力的相对平均误差为：

式中：E为相对平均误差；n为求平均的个数；pb为地层原油泡点压力实测值，MPa；pexp为经验公式泡点压力计算值，MPa。

图1给出了常规经验公式在塔里木油区的拟合相对误差，计算统计如下。STANDING与AL-MARHOUN经验公式在泡点压力介于0～25 MPa时拟合一般，相对平均误差分别为22 %、25 %；当泡点压力大于25 MPa时拟合略优于0～25 MPa，相对误差平均值分别为16 %、14 %。GLASO与LASATER经验公式在泡点压力介于0～30 MPa时，平均误差分别高达29%、31%；当泡点压力大于30 MPa时，各公式拟合程度都非常差且无规律性，误差最大超过100%。

图1 各经验公式拟合相对误差对比Fig.1 Comparison of fitting error of different empirical formula

从各经验公式误差低于5%的井数在塔里木油区总井数的占比情况（图2）可以看出：误差低于5%的井数所占比例最高为24%，最低为14%，因此，以上经验公式难以适用于塔里木油区地层原油，尤其是高温高压油藏条件下泡点压力的预测。

图2 各经验公式计算误差小于5%的井占比Fig.2 Proportion of wells with calculation error of empirical formulas below 5%

基于上述经验公式存在的不足，选取溶解气油比、地层温度、原油中C7+相对分子质量、原油中挥发组分CH4（C1）、中间组分（CO2和C2—C6）的摩尔分数、溶解气相对密度、地面脱气原油相对密度、临界压力以及临界温度10个影响泡点压力的敏感因素[10]，基于共轭梯度法建立了10参数泡点压力预测模型，并对其可靠性进行了验证。

2 塔里木油区泡点压力模型的建立

2.1 各影响因素的确定及定性描述

通过逐步回归的方法进行各参数与泡点压力的定性分析[11-15]。逐步回归的基本思想是通过剔除变量中不太重要又和其他变量高度相关的变量，降低多重共线性程度。将变量逐个引入模型，每引入一个解释变量后都要进行F检验（联合假设检验），并对已经选入的解释变量逐个进行t检验，当原来引入的解释变量由于后续解释变量的引入变得不再显著时，则将其删除，以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程，直到既没有新的显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，以保证最后所得到的解释变量集是最优的。此过程通过软件1stOpt完成。

图4 气油比与泡点压力关系Fig.4 Relation between bubble point and formation gas oil ratio

为研究10个影响因素与泡点压力的定性关系，绘制10个影响因素与泡点压力关系图（图3—图7），直观描述泡点压力与各个因素之间的相关关系。

图3 地层温度与泡点压力关系Fig.3 Relation between bubble point pressure and formation temperature

图5 溶解气和脱气原油相对密度与泡点压力关系Fig.5 Relation between bubble point pressure and relative density of dissolved gas and crude oil

图6 临界压力和临界温度与泡点压力关系Fig.6 Relation between bubble point and critical pressure and critical temperature

图7 原油不同组成摩尔分数与泡点压力关系Fig.7 Relation between bubble point and mole fraction of crude oil with different composition

通过对现有的PVT的实验数据以及对经验公式的模型进行相关性分析，结合图3—图7可以得出以下认识：

1）原油泡点压力的影响因素包括流体性质、地层条件、溶解气的性质以及溶解气的组成[16]。

2）在其他因素不变的条件下，泡点压力与临界温度有明显的负相关关系，泡点压力随着临界温度的增大而减小。

3）在溶解气组成及性质和地层温度不变的条件下，原油中的中间烃组分（C2—C6）含量越高，相对分子质量越小，泡点压力越低，原油中重质含量（C7+）越高，泡点压力越低[17-18]，此外，泡点压力值与N2和C1含量呈正相关关系。

4）地层温度、溶解气性质及组成不变的条件下，原油泡点压力与溶解气相对密度及临界压力呈负相关关系。

鉴于以上因素，建立的预测泡点压力的模型包括以下4个因素：①溶解气油比；②地层条件（地层温度以及临界温度、临界压力）；③溶解气的组分性质；④原油组分性质。

2.2 模型建立的理论基础

共轭梯度法[19]（Conjugate Gradient）是求解数学特定线性方程组的数值解的方法，作为介于最速下降法与牛顿法之间的一种迭代方法，它仅需利用一阶导数信息。不但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点。共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解决大型非线性最优化问题的算法之一。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

对于大规模无约束优化问题，共轭梯度法的求解公式可简述为：

函数f()

x在Rn→R连续可微。其迭代公式为：

ak是搜索步长，由某种线索确定；dk是第k次的搜索方向，其迭代公式为：

gk+1是函数f在xk+1处的梯度∇f(xk+1)，βk+1∈R。多次迭代计算可得出函数的最优解。

2.3 新模型的建立

由于塔里木油区油藏的复杂性，基于泡点压力的影响因素分别做了高压和低压模型，建立了塔里木油区油藏泡点压力预测模型，根据地层已有资料快速准确地计算泡点压力值。

根据塔里木油区132个样品PVT实验数据，对5个常规经验公式在塔里木油区的拟合进行对比分析（图8—图12）。

图8 STANDING经验公式拟合对比Fig.8 Fitting result based on STANDING empirical formula

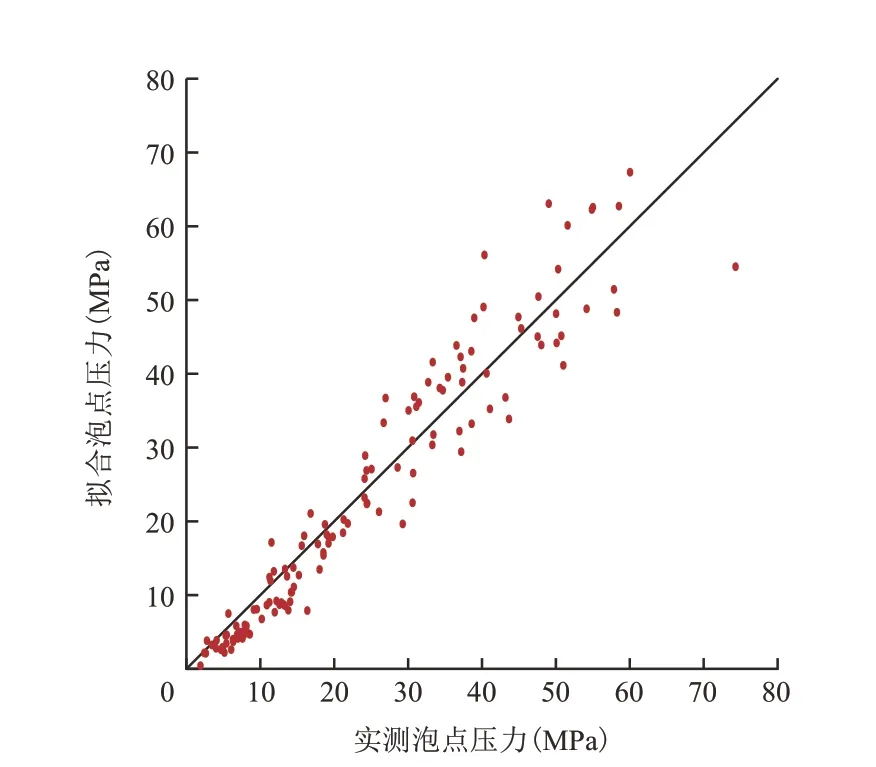
图12 AL-MARHOUN经验公式拟合对比Fig.12 Fitting result based on AL-MARHOUN empirical formula

采用共轭梯度法[19]（CGM）结合通用全局优化算法（UGO）对该模型进行非线性回归及拟合。设定未知数P1—P10与泡点压力影响因素对应，见表3。

表3 泡点压力的影响因素Table 3 Influencing factors of bubble point

通过5种不同经验公式在该区的拟合误差分析，可以发现常规经验公式（尤其是DOKLA-QSMAN经验公式）在低压和高压条件下的拟合误差有明显的区别。对各个影响因素进行泡点压力的初步拟合，通过改变参数的相关关系和参数数据，整体拟合度较低，根据大量数据在塔里木油区拟合结果的认识[20]：以泡点压力等于10 MPa为分界线，几种不同经验公式拟合泡点压力误差相差较大。将油区数据以10 MPa为界线，按照低压和高压分别拟合2种不同模型，发现拟合效果均非常好。其拟合公式和参数的最优解如下：

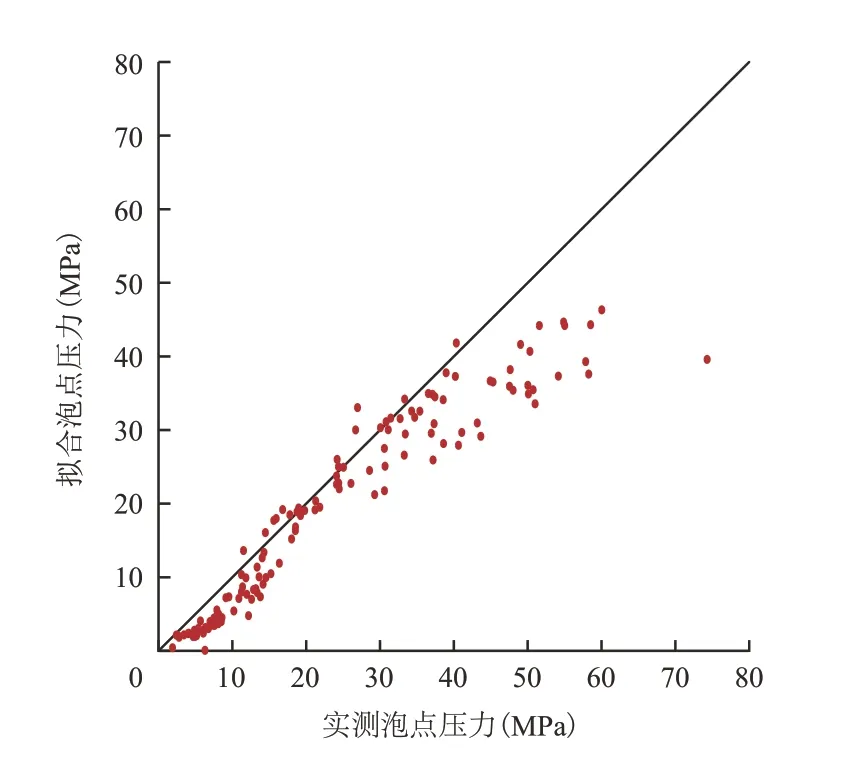
图9 LASATER经验公式拟合对比Fig.9 Fitting result based on LASATER empirical formula

图10 GLASO经验公式拟合对比Fig.10 Fitting result based on GLASO empirical formula

图11 DOKLA-QSMAN经验公式拟合对比Fig.11 Fitting result based on DOKLA-QSMAN empirical formula

1）低压条件（pb＜10 MPa）

式中：pb为地层原油泡点压力，MPa；Rs为溶解气油比，m3/m3；γg为天然气的相对密度；γo为地面脱气原油的相对密度；T为地层温度，℃；mC7+为C7以上的组分的摩尔百分数，%；为氮气与CH4的摩尔百分数，%；mCO2为二氧化碳组分的摩尔百分数，%；为中间烃C2、C3、C4、C5和C6的摩尔百分数，%；pcr为临界压力，MPa；Tcr为临界温度，℃；P1—P10为模型参数。

2）高压条件（pb≥10 MPa）

然后对2种模型进行求解，通过运行计算，迭代出低压条件下，即pb＜10 MPa时方程各系数的最优解（表4）。

表4 低压条件下（pb＜10 MPa）模型参数的最优解Table 4 Optimal solution of model when bubble point is below 10 MPa

该模型的表达式为：

同理，高压条件下，即pb≥10 MPa时各参数最优解见表5。

表5 高压条件下pb≥10 MPa模型参数的最优解Table 5 Optimal solution of the model when bubble point is greater than or equal to 10 MPa

该模型的表达式为：

2.4 新泡点压力模型预测效果验证

基于新的模型，对实验所用塔里木油区现有物性数据进行拟合，拟合结果见图13。

图13中横坐标为实测泡点压力值，纵坐标为拟合泡点压力值，并添加Y=X的辅助线。不同系列的散点对辅助线Y=X的靠近程度可表示其拟合好坏，在辅助线上越聚集代表拟合程度越好，越分散代表拟合程度越差。从图13可以看出该模型对于塔里木油区泡点压力拟合非常好，经计算，该模型相关系数为0.958 3，能真实地反映泡点压力与地层温度、溶解气油比以及溶解气气体性质的关系。为了验证该模型是否能够预测泡点压力，基于塔里木油区的现场油样进行了另外10组的PVT实验，实验所得数据见表6。