基于相对速度和位置辅助的无人机编队协同导航

郭鹏军， 张 睿， 高关根， 许 斌

(1. 西北工业大学 自动化学院， 西安 710072； 2. 航空工业西安飞行自动控制研究所， 西安 710065)

近几年来随着科学技术不断发展，无人机(Unmanned Aerial Vehicle, UAV)在军事和民用领域应用越来越广泛.单个无人机执行任务能力有限，相比之下，无人机编队协同工作具有任务完成率高、功能性强和优化任务分配等优点.实时获取高精度导航信息是无人机编队飞行的可靠保障[1-2].目前，主流的无人机编队导航方式是全球导航卫星系统(Global Navigation Satellite System, GNSS)和惯性导航系统(Inertial Navigation System, INS)组合导航，利用GNSS信号修正惯性设备的漂移误差.但复杂战场环境或外界遮挡环境可能导致GNSS不可用，其惯性导航在长时间运行中会导致误差积累，若编队都采用高精度的惯性器件，飞行成本会大幅增加.

无人机协同导航利用各成员自身导航信息以及各成员之间的相对导航信息共享来抑制惯性导航的解算误差.根据编队内的信息交互架构，可将无人机编队方式分为平行式[3-4]和主从式[5-6].平行式以去中心化为思想，各成员任务等级相同；而主从式编队中，成员分为长机和僚机，在全球定位系统(Global Positioning System, GPS)拒止环境中，长机和僚机通过机载数据链进行导航信息的交互[7]，长机可在敌方防控区域外进行巡航，而由僚机进入拒止区域进行侦察和打击[8].协同导航技术主要涉及相对导航方式[9-10]、编队构型、集群信息交互和定位导航算法等技术[11-12].目前针对协同导航已有一定研究，文献[13]依据无线信号的接收角度和信号强度得到方位距离，并基于几何关系进行求解，但该模型为二维陆地机器人编队模型，无法应用于高机动特性的三维无人机编队；文献[14]基于联邦滤波提出无人机集群分层式协同导航模型，提高了编队导航的容错能力，但其协同导航模型只对其速度和位置误差进行估计，并未考虑相对传感器误差以及僚机失准角的校正，无法满足长航时的导航需求.

本研究针对主从式无人机编队形式提出一种相对速度和位置辅助的无人机协同导航方案.首先，在考虑相对导航传感器误差的前提下，结合惯性导航的误差方程建立协同导航系统的状态方程；其次，将相对导航信息与绝对导航信息进行空间统一，建立相对速度和相对位置综合量测模型；最后，利用卡尔曼滤波器估计僚机的导航误差并进行误差补偿，提升各僚机的导航精度.

1 协同导航系统方案设计

协同导航系统方案基本思路如图1所示.图中：M为长机；Sn为僚机，n∈N；SINS为捷联惯导系统.编队中长机通过组合导航提供自身高精度的导航信息，并通过机载数据链与各个僚机进行导航信息共享.然后，以僚机INS的误差模型、多普勒测速误差模型以及激光测角和测距误差模型组合建立系统的状态方程，僚机通过相对导航传感器可测得自身与长机的相对速度和位置信息，结合接收到的长机导航信息可推算出僚机的速度及位置信息，将其与僚机惯导输出的速度位置作差，从而建立协同导航系统的量测方程.利用协同导航滤波器估计出僚机INS的误差以及相对传感器的测量误差，通过反馈对僚机INS以及相对导航传感器进行补偿，抑制僚机惯导的漂移，从而提升无人机集群的导航精度.

图1 无人机协同导航方案框图Fig.1 Diagram of UAV cooperative navigation scheme

2 相对导航传感器误差模型

2.1 多普勒测速误差模型

根据多普勒测速原理以及相应的误差来源可将机载三维多普勒测速装置的速度测量值表示为

vd=(I+δA)(I+δK)(vt+δv)

(1)

式中：I为3×3的单位矩阵；vt为速度真实值；δA为三轴安装误差；δK为测速刻度因数；δv为三维速度随机误差，相应值为

由于式(1)中误差都为小量，展开后忽略耦合项可得：

vd=vt+δAvt+δKvt+δv

(2)

因此，选择多普勒测速仪的测速误差状态为

XDVL=

[δKxδKyδKzδAxδAyδAzδvxδvyδvz]T

(3)

式中：δKi和δAi为随机常量，δvi为随机测速误差，i=x,y,z，可由一阶马尔可夫过程近似描述.

多普勒测速仪的误差状态方程为

(4)

式中：

τx,τy,τz和wx,wy,wz分别为多普勒测速误差模型一阶马尔可夫过程的相关时间和白噪声.

2.2 激光测距和测角误差模型

激光雷达采用激光飞行时间法测距，测距公式如下：

(5)

式中：Lt为距离测量真实值；Δt为激光来回的传播时间；c为激光束在真空中传播的速度；n为大气折射率；N为激光束的脉冲总数；T0为激光的脉冲长度.当考虑回波强度对测量距离产生的随机测量误差时，激光测距的相对距离测量值可表示为

L=Ltkl+δl

(6)

式中：kl为修正系数，是随机常数；δl为波强的随机测量误差.

激光测角使用波达角度传感器进行测量，如激光测角传感器等，其测量值可表示为

αc=αt+δα

(7)

式中：αt为角度真实值；δα为角度测量的随机误差.

因此，选择激光测角和测距传感器误差状态量为

XR=[klδlδα]T

(8)

式中：δl，δα由一阶马尔可夫过程近似描述.因此激光测角和测距误差状态方程为

(9)

式中：

τl,τα和wl,wα分别为激光测距和测角误差模型一阶马尔可夫相关过程时间和驱动噪声.

3 相对导航矢量模型计算

由于相对导航传感器的输出是载体坐标系(b系)下的相对导航信息，而惯导解算出的信息为导航坐标系(n系)下的绝对导航信息，所以需将相对导航信息进行空间统一.

3.1 b系下相对导航矢量模型

选用地理坐标系为导航坐标系，僚机搭载的相对导航传感器在b系测得的相对导航信息可根据测距、测角和测速模型分别表示为

(10)

3.2 相对导航矢量模型空间转换

(11)

将式(10)代入式(11)，同时忽略二阶小量，可得：

(12)

式中：δpbx,δpby,δpbz为伪量测噪声.

(13)

图2 僚机b系下相对导航矢量Fig.2 Relative navigation vector in b coordinates of slave

3.3 相对位置矢量和惯导输出位置转换

僚机INS输出的三维位置信息为纬、经、高度，而相对导航传感器输出的三维位置信息为3个方向的距离.由于无人机编队间距远小于地球直径，所以长、僚机间的直线距离可近似为以地心为圆心过二者的弧线长度，则相对导航推算的僚机纬、经、高度信息可表示为

(14)

式中：R为地球半径；LM,λM,hM为长机纬、经、高度.

4 协同导航系统的数学模型

4.1 协同导航系统的状态方程

联立多普勒测速的误差模型、激光测距误差模型，并参考文献[15]中的僚机惯导误差方程，得到协同导航系统的状态方程：

(15)

式中：

4.2 协同导航系统的量测方程

在n系中，僚机通过机载数据链接收长机的导航信息，与僚机测量的相对导航信息作差可得僚机的推算导航信息，再通过僚机自身INS信息与推算的僚机导航信息相减得到量测结果.因为长机定位较为精确，所以对其误差进行忽略，即

(16)

4.2.1速度量测矩阵 由b系下的速度误差模型可知：

(17)

(18)

式中：Φ×为失准角矢量Φ的反对称矩阵，即

(19)

联立式(18)和式(13)，并忽略二阶耦合项，n系下相对速度的测量值可表示为

(20)

(21)

则速度观测量可表示为

(22)

将Φ×,δA,δK分别代入式(22)可得：

Zv=HvX+Vv

(23)

4.2.2位置量测矩阵 n系下相对位置信息可表示为真实信息和误差之和：

(24)

将式(24)带入式(14)，可得到僚机的相对导航推算的纬、经、高度信息：

(25)

此外，僚机惯导输出的位置信息可表示为真实纬、经、高度信息与对应误差之和：

(26)

将式(25)和(26)代入式(16)，可得到位置量测矩阵为

Zp=HpX+Vp

(27)

4.2.3协同导航系统的量测方程 联立式(23)和式(27)，协同导航系统的观测矩阵为

(28)

根据状态方程和量测方程，利用卡尔曼滤波对相对导航传感器以及僚机惯性导航的误差进行估计并校正.

5 仿真及结果分析

为验证所提协同导航算法的有效性，搭建长机、僚机无人机编队协同导航验证平台.为有效描述无人机集群间的相对位姿，长机、僚机的相对位姿都由编队参考点给出，其参考点导航信息取(34°, 108°, 100 m)，相对导航传感器配置如表1所示.此外，实际主从式无人机编队中，长机搭载高精度惯性导航，而僚机搭载低精度的惯性导航.因此，在仿真中长机配置高精度INS，比僚机INS精度高10～20倍，长机、僚机的导航参数配置如表2所示.

表1 相对导航传感器配置Tab.1 Configuration of relative navigation sensor

表2 编队成员导航参数配置

根据无人机编队要求，设置单长机三僚机的无人机编队，通过轨迹发生器设计编队飞行轨迹，编队先后进行加速、爬升、匀速、转弯等机动形式.此外，为保持编队队形，设计僚机飞行轨迹与长机同步，飞行过程中编队构型不发生改变，僚机的运动轨迹与长机同步，设置仿真时长为 1 800 s，其在导航坐标系中的轨迹曲线如图3所示，曲线均为无人机相对于参考点的真实飞行轨迹.

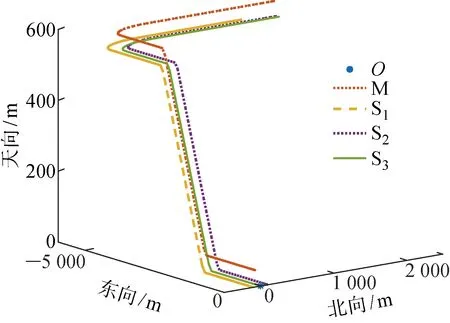
图3 长机和僚机真实轨迹Fig.3 Real trajectory of leader and slave

编队以图3设计的轨迹飞行，其中长机配备表2中对应的高精度惯性器件和GPS进行组合导航，其组合导航在各方向上的速度误差小于0.02 m/s，定位误差小于3 m；为与所提协同导航方案进行对比，首先各僚机S1, S2, S3仅采用表2中对应的低精度INS进行导航，经过 1 800 s 飞行，得到误差曲线如图4～6所示，图中：t为仿真时间；δA为纯惯导解算的失准角误差；δv为纯惯导解算的速度误差；δp为纯惯导解算的位置误差；δθ，δγ，δψ分别为僚机东、北、天方向的失准角误差；δve，δvn，δvu分别为僚机东、北、天方向的速度误差；δL，δλ，δh分别为僚机北、东、天方向的位置误差.其纯惯导解算东向、北向速度误差发散至1 m/s和0.5 m/s，东向、北向位置误差发散至600 m和400 m，僚机的惯性导航天向速度、位置与气压高度计利用卡尔曼滤波进行融合，使其误差收敛，从整体精度来看各僚机纯惯性导航定位精度无法满足长时间编队飞行导航的要求.

图4 僚机S1惯性导航解算误差Fig.4 Error of inertial navigation solution of Slave S1

图5 僚机S2惯性导航解算误差Fig.5 Error of inertial navigation solution of Slave S2

图6 僚机S3惯性导航解算误差Fig.6 Error of inertial navigation solution of Slave S3

图7 僚机S1协同导航误差Fig.7 Error of cooperative navigation of Slave S1

图8 僚机S2协同导航误差Fig.8 Error of cooperative navigation of Slave S2

图9 僚机S3协同导航误差Fig.9 Error of cooperative navigation of Slave S3

6 结语

针对主从式无人机编队形式提出一种无人机协同导航方案，利用僚机的惯导误差量以及相对传感器的误差量建立协同导航的系统模型，对相对速度以及相对位置构建量测方程.在此基础上，通过卡尔曼滤波对误差进行估计，以此对僚机惯导以及相对导航传感器误差进行补偿，为无人机编队提供稳定可靠的导航信息.