不同送风方式下大客车内飞沫传播特性研究
2022-12-01陈志鑫汪怡平杨亚锋苏建军
陈志鑫, 汪怡平, 杨亚锋, 苏建军, 杨 斌
(1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室, 武汉 430070;2. 湖北省齐星汽车车身股份有限公司,湖北 随州 441300;3. 甘肃建投重工科技有限公司, 兰州 730000)
近年来,通过空气传播的呼吸道传染疾病日益增多,例如结核病、严重急性呼吸系统综合征、禽流感、猪流感(H1N1)和新型冠状(以下简称新冠)病毒肺炎(COVID-19)等.2019年底爆发的新型冠状病毒及其变种至今仍在全球肆虐,已夺去数百万人的生命,疾病引发的疫情对公众健康和社会经济造成严重负担[1].呼吸道传染病病毒通常以人体呼出的飞沫为载体[2],在不同的室内环境中,这些携带病毒的飞沫会蒸发、悬浮在空气中,随后被人体吸入,从而产生潜在的感染风险.大客车作为人员密度高且封闭的空间,普遍存在通风不足问题,极易引发呼吸道传染疾病的传播.2020年1月湖南发生的一起在公共汽车内的疫情显示,在4 h的旅程中,45名乘客先后有8人被感染新冠病毒[3];2020年12月,在石家庄一辆承载40余人的大巴车中,包括司机在内的6人新冠病毒检测呈阳性[4].因此,有必要进一步深入研究大客车的气流组织形式及飞沫的扩散特性.
目前,人体呼出飞沫在密闭空间扩散的研究主要集中在建筑物内以及飞机机舱[5-6],对于其在大客车内的扩散研究较少.Yang等[7]分析了送风角度、相对湿度和飞沫尺寸对飞沫在车内传播的影响,其研究表明高湿度环境、向后排送风可以有效降低飞沫传播的感染风险.Zhang等[8]研究发现,开启门窗可以降低客车内50%的飞沫体积分数,但可能会增加门窗附近处乘客的感染风险.Zhu等[9]通过对比公交车常用的几种通风方式,发现采用置换通风可以降低呼吸道传染疾病在公交车内的感染风险.但这些研究对于揭示飞沫扩散机理与客车送风形式、车内流场之间的内在联系不够深入.
因此,本文拟采用计算流体力学(CFD)的数值仿真方法,获取大客车气流组织特性,基于拉格朗日方法,研究送风方式对飞沫扩散的影响,结合Wells-Riley方程,评估不同送风方式下大客车内乘客的感染风险,为客车送风系统的结构设计和降低空气传播感染风险提供指导作用.
1 流场计算控制方程及感染预测方法
1.1 湍流模型
准确的预测室内气流组织是探究飞沫传播规律的前提.研究结果表明[10],对于封闭空间内气流组织的模拟,RNGk-ε湍流模型具有较高的精度.因此选取RNGk-ε湍流模型计算车内流场,表达式为
Gk+Gb-ρε-Ym+Sk
(1)
(2)
式中:k为湍流动能;ε为湍流耗散率;ui为时均速度;μt为涡黏性系数;ρ为空气密度;t为时间;xi和xj为坐标方向;Gk和Gb分别为速度梯度和浮力引发的湍流动能;Ym为由扩散引发的波动;C1ε=1.42;C2ε=1.68;C3ε=tanh|vc/uc|,vc为平行于重力矢量的速度分量,uc为垂直于重力矢量的速度分量;αk和αε分别为k和ε方程的有效湍流普朗特数的倒数,αε=αk=1.39[11];Rε为附加项;Sk和Sε为用户自定义源项.
壁面对湍流流动有明显影响,沿着壁面的法向方向,湍流分为近壁面区和完全发展的核心区.RNGk-ε模型针对的是充分发展的湍流,对于近壁面区,本文选取标准壁面函数法,此时需引入无量纲距离,表达式为
(3)
式中:Δy为距离壁面距离;τw为壁面切应力;V为运动黏度.使用标准壁面函数法一般要求y+处于10~250之间[12].
1.2 颗粒轨道模型
为了研究飞沫在客车内的运动状态及随时间变化分布情况,选用颗粒轨道模型.颗粒轨道模型是基于拉格朗日体系,从牛顿运动定律出发建立颗粒运动方程来模拟颗粒物的运动情况,其颗粒轨道的运动方程为

(4)
(5)
式中:up为粒子速度;FD为空气与粒子相对滑动引起的曳力;u为空气流速;g(ρp-ρ)/ρp为重力项,g为重力加速度,ρp为粒子的密度;Fad为附加力项;μ为空气的动力黏度;dp为粒子直径;CD为曳力因数;Rep为颗粒雷诺数,Rep=(u-up)dp/μ.
考虑湍流脉动对颗粒扩散的影响,选用随机轨道模型描述颗粒物的运动[13].
1.3 Wells-Rily方程
1955年Wells与Riley提出Wells-Riley方程[14-15]用于估算传染性疾病在室内传播的概率,该方程假设病毒颗粒物在空气中均匀混合、无生物衰减且不受过滤和沉降作用的影响,表达式为
(6)
式中:P为易感人员感染概率;I为感染者数量;q为感染者呼出病毒颗粒数量;p为易感染人员的呼吸流量;t′为总暴露时间;Q为通风装置供气速率;Ns为易感染人员吸入的病毒颗粒数量.假设所有乘客处于相对安静状态,参照文献[16]p为10 L/min,感染者每次咳嗽呼出飞沫中包含病毒颗粒数量q为10个.
在实际情况中,病毒颗粒物在客车中并非均匀混合,故Gupta[17]提出了非均匀混合条件下吸入的病毒颗粒物数量的计算方法为

(7)
式中:dl(t)为0至t0时间内某名乘客吸入病毒颗粒物总量;v(t)为乘客呼吸区域中的飞沫体积分数;f(t)为病毒的活性,通常取1;c为病毒在飞沫中的体积分数.通过仿真计算可以获取不同时刻乘客呼吸区域内飞沫颗粒物的数量,通过式(6)获取感染者在一次咳嗽过程中其他乘客吸入的病毒颗粒物数量.假设一次行程为3 h,感染者每小时咳嗽25次,通过叠加的方法获取整个行程中吸入的病毒颗粒物数量,代入式(6)可以计算得到各个位置的乘客感染概率.
2 车内流场计算设置
2.1 研究对象
研究对象为一辆长11 m的47座大客车.依据送风方式不同构建了4个模型,如图1所示.模型1的送风方式为上送上回,气流通过顶部92个离散分布的送风口进入舱内,在靠近中门的顶部集中回风;模型2的送风方式为上送下回,送风口与模型1相同,回风口位于两侧壁面距离地板10 cm处;模型3的送风方式为上送下回,采用条缝型送风口,回风口与模型2相同;模型4送风方式为置换通风,送风口位于壁面两侧,距离地板5 cm,回风口位于两侧行李架.车内座椅布局如图2所示.在所有仿真场景中,假设客车满员,且乘客未在车内行走.乘客呼吸区域如图3所示.

图1 客车4种不同送风方式Fig.1 4 different air supply mades for buses

图2 大客车内座椅布局Fig.2 Seat layout in bus

图3 乘客呼吸区域 (m)Fig.3 Breathing area for passengers (m)
2.2 数值求解设置
采用ANSYS Fluent软件进行模拟计算.假设感染者咳嗽发生前车内空气洁净,根据Agrawal等[18]的研究,一次咳嗽产生的飞沫颗粒物粒径范围为0.5~1 000 μm,粒径大于50 μm的颗粒受重力影响会迅速沉降,较小的颗粒(0.5~10 μm)会在空气中长时间悬浮.在一次咳嗽中,4~8 μm的飞沫数量占比最高,故本文选择粒径为5 μm的飞沫为研究对象.设置飞沫质量流量为1.176×10-6kg/s,密度为980 kg/m3,飞沫向下30° 喷射,飞沫的初始速度随时间变化曲线如图4所示[17],当t=0.08 s时,速度达到峰值9 m/s.仿真设定飞沫颗粒物一旦接触壁面或人体表面即发生沉降[19].4个模型设置保持送风流量一致,具体边界条件设置如表1所示,求解器设置如表2所示.

图4 飞沫初速度随时间变化曲线[17]Fig.4 Droplet initial velocity versus time[17]

表1 边界条件设置Tab.1 Boundary condition settings

表2 求解器设置Tab.2 Solver settings
2.3 模型验证与网格划分
本文模拟了空气中飞沫颗粒的扩散特性,与Liu等[22]的研究模型进行对比.在长宽高为 4 m×2 m×3 m的矩形空间内,环境温度为25 ℃,相对湿度为0%,喷嘴的水力直径为0.02 m,初始粒径为 20 μm 的颗粒物以10 m/s的初速度向空气中射出.图5中实线为射流边界,Z′为高度,X′为水平距离;图5(a)黑点为文献[22]中模型的结果,图5(b)红点为本文模拟的结果,与文献对比验证的结果良好.

图5 文献模型结果对比图Fig.5 Comparison of literature model results
采用四面体非结构网格对大客车计算域进行离散,为消除网格尺寸对计算结果的影响,划分3种网格进行网格无关性验证,网格数量分别为400万、1 100 万和 2 000 万.发现 1 100 万网格和 2 000 万网格计算结果误差小于5%,故选用的网格数量为 1 100 万,送风口网格尺寸为5 mm,人嘴鼻处尺寸为5 mm,人体和座椅处尺寸为20 mm,壁面尺寸为40 mm. 通过对壁面网格的细化,使y+处于20~130之间.

图6 乘客7前方横截面速度分布图Fig.6 A cross-sectional velocity distribution profile in front of passenger 7
3 结果分析与讨论
3.1 稳态流场分析
为探究客车内飞沫的传播规律,首先计算了客车内部稳态的流场.客车内气流速度的分布如图6和图7所示,图6为乘客7前方0.2 m处横截面速度分布图,其中,v为风速.图7为客车模型内高度Z=0.8 m处截面速度分布图.
由图6可知,模型1采用上送上回的通风方式,空调送风口处有较强的向下气流,由于座椅和送风口的非对称布置,在过道中有一个向上的气流,此截面上大部分区域风速在0.2~0.3 m /s之间.由于模型2和模型3采用上送下回的通风方式,大部分空调的送风可以很快从乘客下方排出舱内,此截面上风速大部分在0.01~0.15 m/s, 模型3中气流在右侧乘客头部形成微弱的涡流.模型4采用置换通风,没有形成明显的涡流,气流可以快速排出客车.
图7所示为客车纵截面的气流速度分布.由于模型1的回风口布置在车顶中部,故舱内存在占主导地位的纵向气流,且此截面上的气流速度高于其他3个模型.模型2和模型3纵截面速度分布显示,由于舱内布置的非对称性,依然存在纵向的气流,但模型3采用条缝型的送风口,纵向气流明显减少.模型4车内没有明显的纵向气流,说明这种通风方式可以很好抑制飞沫在舱内传播.
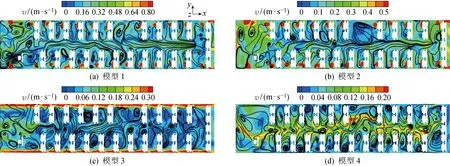
图7 客车Z=0.8 m处截面速度分布图Fig.7 Cross-sectional velocity distribution profile of bus at Z=0.8 m
3.2 车内飞沫扩散分析
模型1采用多排送风、集中回风的送风方式,如图8所示.因此当感染者位于客车内不同位置时,飞沫传播特性会有较大差异,分别截取5、20和40 s的飞沫扩散特征图,红色部分为5 μm的飞沫在空间上的位置状态.如图8(a)所示,在5 s时,7号乘客感染者咳嗽产生的飞沫主要聚集在感染者前方,飞沫随着气流向过道扩散,受车内纵向气流的影响,有向后排扩散的趋势. 在20 s时,飞沫向后移动,在客车前舱混合并扩散至回风口附近,随气流开始排出客舱.在40 s时,模型1中还剩10%的飞沫,分布在客车前7排.当23号乘客为感染者时,飞沫在回风口附近区域快速混合后从回风口排出,没有扩散至其他区域;当42号乘客为感染者时,咳嗽产生的飞沫主要分布在客舱后6排,在20 s时开始随气流排出客舱.

图8 模型1中不同位置感染者产生飞沫扩散侧视图Fig.8 Side view of droplet diffusion from infected individual at different positions of Model 1
仿真结果表明,飞沫在舱内分布特性与回风口位置和气流组织等因素密切相关.飞沫扩散至回风口另一侧区域的比例较小,当回风口与感染者距离较远时,病毒颗粒会在客车内扩散,从而影响到更多的乘客.
由于模型2、3和4的回风口均匀布置在乘客下方或者上方,不同位置的流场结构类似,故讨论7号乘客为感染者的飞沫扩散情况.如图9所示,在5 s时,咳嗽产生的飞沫主要聚集在感染者前方,飞沫随气流扩散,并有部分飞沫到达回风口附近,开始排出客车.

图9 7号乘客为感染者时不同模型飞沫扩散侧视图Fig.9 Side view of droplet diffusion of different models when passenger 7 is infected
在20 s时,模型2中的飞沫受向上和向后的微弱气流影响,扩散至感染者后两排.采用条缝型送风口的模型3和模型4中飞沫没有向后扩散,主要聚集在第2排附近.
在40 s时,模型2中还剩18%的飞沫,剩余飞沫主要分布在客车前6排.模型3中剩余飞沫聚集在前4排,还剩28%的飞沫.图6中模型2和模型3中大部分飞沫可以随着空调送风很快从乘客下方排出舱内,但是在过道中存在向上的气流,并形成很多明显的涡流,飞沫扩散后容易在过道上方附近聚集.模型2和模型3过道附近风速小于模型1,飞沫沉降和排出客舱的速度慢于模型1,故在40 s时模型2和模型3相较模型1剩余更多飞沫.模型4中仅剩5%的飞沫,且飞沫主要聚集在感染者周围,没有向左侧和后方扩散,表明置换通风一定程度上限制了飞沫在客舱内的扩散.
3.3 感染概率预测
图10为在4种送风方式下,不同位置感染者导致乘客的感染概率.在模型1中,乘客的感染风险与感染者的位置相关,位于前部(7号)和后部(42号)的感染者,因车内产生明显的纵向气流,咳嗽产生的飞沫在客车内扩散影响到更多的乘客,分别导致位于感染者与回风口之间32%和31%的乘客感染概率大于5%,而位于回风口下方的23号感染者仅造成12%的乘客有较高感染风险.

图10 4种送风方式下乘客感染概率Fig.10 Probability of infection of passengers in four air supply modes
在模型2、3和4中,感染高风险区域集中在感染者附近.模型2中感染者产生的飞沫导致29%的乘客被感染风险在5%~36%之间.而将非对称布置的圆形送风口改为条缝型送风口的模型3,乘客感染风险有所改善,7号感染者产生的飞沫导致乘客感染概率最高为17%,车内仅有15%的乘客有较高的风险被感染.在采用置换通风的模型4中,42号感染者产生的飞沫导致43号乘客有55%的感染概率,7号感染者产生的飞沫导致6号乘客被感染的概率高达60%,但仅6%的乘客有高于5%概率被感染,94%的乘客被感染概率几乎为0,说明置换通风能够很好地限制飞沫在客车内的传播,并及时将飞沫排出舱内.
在湖南出现的公交车内新冠疫情传播案例中,公交车采用与模型1相同的送风策略[3],感染者距离回风口较远,推测是由于车内存在强烈的纵向气流,粒径较小的飞沫颗粒在车内扩散,导致与感染者间隔7排的乘客吸入病毒被感染.研究表明,条缝型送风口可以使客车内纵向气流减少,乘客的被感染风险有所改善,尤其是在采用置换通风的客车内,94%乘客的被感染概率几乎为0.
4 结论
本文采用CFD的数值仿真与Wells-Riley方程相结合,对4种通风方式下客车内飞沫扩散以及乘客感染风险进行研究.揭示飞沫扩散机理与客车送风形式、车内流场之间的内在联系,对客车送风系统的结构设计和降低空气传播感染风险提供指导作用,结论如下:
(1) 飞沫在舱内分布特性与感染者位置、回风口位置和气流组织等因素密切相关.当回风口与感染者距离较近时,病毒颗粒会很快从回风口逃逸到外界.
(2) 客车内的纵向气流是影响飞沫扩散的关键因素,当客车内存在强烈的纵向气流,会导致飞沫在客车内扩散,从而使更多乘客有被感染风险.研究发现,条缝型送风口相较于非对称布置的圆形送风口能够减少车内的纵向气流.
(3) 在4种送风方式中,置换通风能够最大限度减小客车内空气与飞沫的混合,减少飞沫与大部分乘客的接触,降低车内乘客被感染的风险.
