基于R-NSGA-III 的常规导弹火力分配模型
2022-12-01刘子豪董宝良王宝宝廉兰平程灿
刘子豪,董宝良,王宝宝,廉兰平,程灿
(华北计算技术研究所系统四部,北京 100083)
常规导弹作战方案评估主要是对常规导弹部队作战方案的可行性、风险度、作战效益等进行的评价和估量[1]。如何提升作战方案的可行性、作战效益,降低风险度是研究重点和难点。
文献[2]提出综合考虑目标重要度、毁伤要求以及生存状态等因素建立了辅助决策模型,文献[3]提出建立了针对防御场景下的动态武器协同火力分配模型,该文在其基础上考虑了某型号导弹存在调度转移[4]和发射前准备时间等情况,在普通武器-目标模型[5]的基础上,引入了导弹发射准备时间(时间成本)这一目标,辅助决策者选择评估价值更高的方案。
武器-目标分配问题主要使用多目标进化算法进行求解,这类算法需要利用帕累托(Pareto)前沿找到相对优解或者最优解。非支配排序遗传算法(NSGA-III)就是其中的典型代表,在处理多目标优化问题上具有较为广泛的应用。但在辅助决策中,决策者并不需要得到全部Pareto 前沿,而只关心部分Pareto 前沿,或者只需要在特定区域获得更多解。基于此,该文提出基于偏好点的NSGA-III 算法(R-NSGA-III)的常规导弹火力分配辅助决策模型,并通过实验仿真验证了模型可以得到最优打击方案,能够达到辅助决策作用。
1 简介
该文提出基于R-NSGA-III 的常规导弹火力分配模型,优化目标包括最大化敌人的预期损失、最小化方案导弹的成本和最小化导弹发射任务准备的时间成本。模型主要针对的场景是在打击目标给定条件下,对现有进入发射状态和未进发射状态的导弹进行任务分配。模型需要决策者输入对三个目标的若干偏好,然后可生成多种近似并相对最优的打击方案,并可以通过三维散点图的方式对生成方案,并直观地展示给决策者,以更好地辅助决策。
该文求解模型的算法是基于NSGA-III 算法进行改进的。当前主流用于解决火力分配的多目标优化算法还有MOEA/D[6]、粒子群[7]、NSGA-II[8]等。其中NSGA-III 算法在处理多目标优化问题上具有较为广泛的研究[8,10-11]与应用[11-12],但是该算法生成的完整Pareto 前沿并不全部是用户关心的。实际上决策者偏好方案一般只集中在Pareto 前沿的部分区域,或者在偏好的区域获得更多的方案等。所以该文采用了R-NSGA-III 算法[13],该算法在NSGA-III 程序的基础上,引入一种新的参考点生成方法,同时使用遗传算子和生存选择过程。
2 导弹目标分配辅助决策模型
2.1 基本假设
假设某次作战行动中有M种可用导弹武器装备,设武器集合为W,其中,wi表示第i类武器装备,且第i类武器装备有Mi个,则第i类武器装备集合wi表示为Wi。有N个潜在打击目标,目标集合为T,其中tk表示第k个潜在打击目标。
文献[14]围绕导弹战斗部打击目标过程所涉及的毁伤评估研究进行总结概述,分别从目标毁伤评估模型、毁伤过程主体、分类目标毁伤、毁伤评估手段四方面进行阐述,梳理现有的主要成果。可抽象计算出第i类武器装备打击第k个打击目标时的毁伤概率为pik,毁伤收益为vi,使用一个第i类导弹装备所需要的成本为uj。参考文献[15]和文献[17]模型设导弹wij进入发射状态所需时间为sij。
2.2 问题模型
M类武器联合打击所有潜在的目标时,对目标的毁伤效果如式(1)所示:
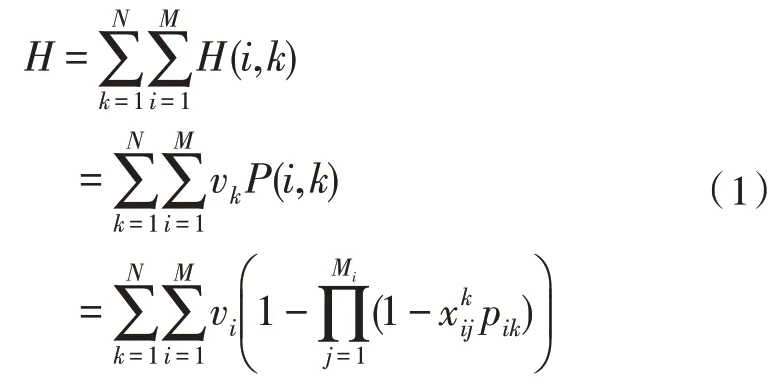
M类武器联合打击所有目标时,成本为使用的所有武器的成本之和,如式(2)所示:
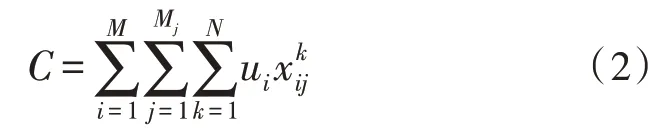
方案的导弹准备时间取导弹进入发射前的平均等待时间,如式(3)所示:
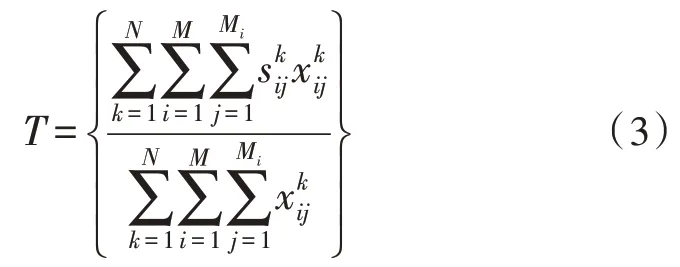
2.3 问题约束
确定武器装备目标分配方案时需要满足一些约束条件,建立优化模型的约束条件如下:
约束a:对于任意一个武器装备,最多只能打击一个目标,即一个武器装备可以用于打击某个目标,也可以闲置不打击某个目标,如式(4)所示:
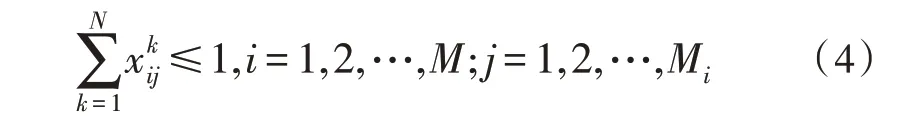
约束b:用于打击同一目标的武器装备种类数不超过某一阈值(假设预先设置的阈值为T),如式(5)所示:

综上,根据给出的目标函数和约束条件,确定武器装备目标分配方案时以最大化单位成本上的毁伤效果为目标的优化模型,如式(6)所示:

3 基于偏好点的NSGA-Ⅲ算法
3.1 NSGA-III算法
2014年,有文献提出了NSGA-III算法,该程序通过引入一系列预定义的参考方向,弥补了NSGA-II无法扩展到三个以上目标的不足。该算法根据当前种群获得覆盖整个目标空间的超平面,并在超平面上生成一系列分布均匀的参考点。也有一些文献[19]对该算法进行了改进,为该文提供了思路。由于该文提出的基于偏好点的NSGA-III 方法就是基于这种方法,所以,文中简要描述其过程,算法流程图如图1 所示。
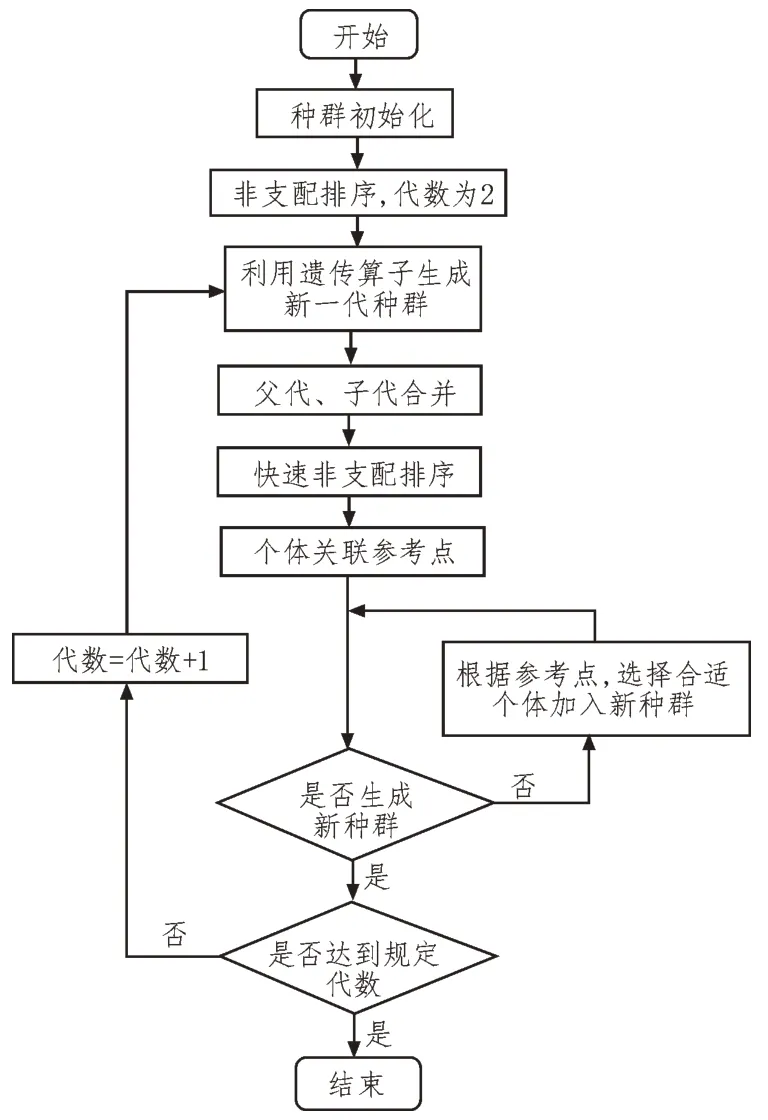
图1 NSGA-III算法流程图
NSGA-III 算法与NSGA-II 算法在父代、子代合并前的操作都是相同的。NSGA-III 算法首先利用Das-Dennis 方法在单位超平面上选取H个分布均匀的参考点,然后将每个参考点与原点相连接,参考方向为目标点方向。在每一代合并后的种群中,所有个体都根据系统的最大、最小值进行归一化。然后,根据个体到参考方向的正交距离,将每个个体关联到一个特定的参考方向,用一种小生境方法来选择合适的个体加入新种群。这种方法不需要额外的选择操作,因为总体大小几乎保持与参考方向的数量相同。NSGA-III 算法在3-15 个目标的优化问题上进行了测试,在每种情况下,它都能够在约束和无约束问题上找到一个收敛良好、分布良好的近Pareto最优解集。
3.2 基于偏好点的NSGA-III
R-NSGA-III 在NSGA-III 的基础上进行了扩展,将决策者提供的偏好点作为参考,引入了一种新的参考点生成方法,同时使用与后者相同的遗传算子和生存选择过程。假设决策者提供了K个三目标模型的偏好点r(k)。
每个偏好点首先采用NSGA-III 的归一化方法进行归一化。根据每个目标的最大值fmax和最小值fmin,得到归一化的偏好点如下:
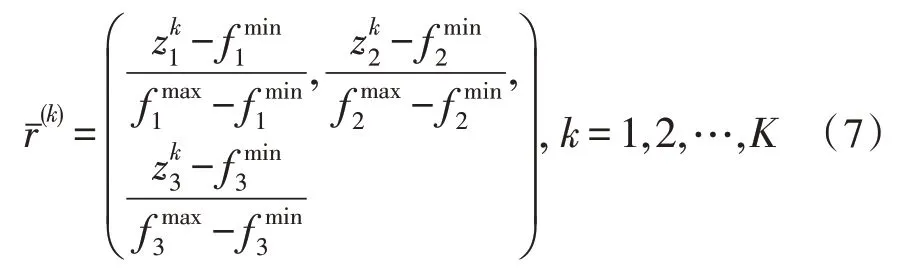
然后,计算单位超平面的截距和从理想点到每个标准化参考点的向量如下:
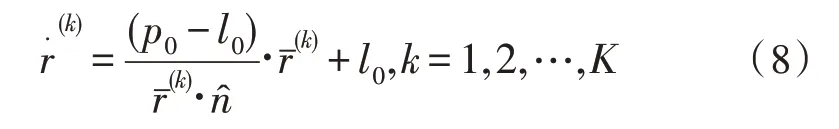

然后,利用Das-Dennis 参考点的质心g和形成的向量,将缩小后的Das-Dennis 参考点平移到单位超平面上,结果如下:

其中,gi为缩小的Das-Dennis 点的质心。
在完成上述操作之后,所有的Das-Dennis 参考点都位于以投影点为中心的三角小区域上。对K个偏好点逐一重复上述步骤。因此,将一共有K×H个参考点存储在Za中。然后将三个由单位向量表示的极值点添加到集合Za上。
这使得Za的大小为(K·H+3)×3。为了后续可以更好地进行归一化,添加极值点来创建极值的Pareto 最优解,并将这些点作为NSGA-III 算法中的参考点。因为标准化因子(fmax,fmin)在每一代中都会发生变化,所以要在每一代中都执行上述操作。在NSGA-III 运行结束时,除了极端参考方向对应的解外,只考虑原始参考点产生的每个参考方向的最接近解。
4 实验结果及分析
4.1 实验算例描述
假设我方本次进攻,拥有5 种导弹类型,每种类型的弹量平均为9 个,期望打击的目标数量为7 个,算法人口为183。该文的初始数据为0 到1 之间随机数。为贴合战场实际情况,在此基础上进行了修改。如选择部分武器进入备战状态,准备的时间成本为0。部分毁伤能力强的武器未进入热待机状态,则准备时间会更长等。
对照组采用了NSGA-III 算法,并采用了相同的种群规模,生成两组实例。决策者根据对三个目标的权衡给出偏好点,如表1 所示。

表1 偏好点
4.2 运行结果分析
为了更直观地进行展示,作图时用点的大小表示时间开销的大小。实例1 两种算法的运行结果如图2-3 所示。
实例2 两种算法的运行结果如图4-5 所示。
如图2-5 所示,该模型可以辅助决策者通过散点图更直观地了解到方案成本与收益的关系,快速地根据战场情况筛选出符合当前时间要求的方案。

图2 NSGA-III
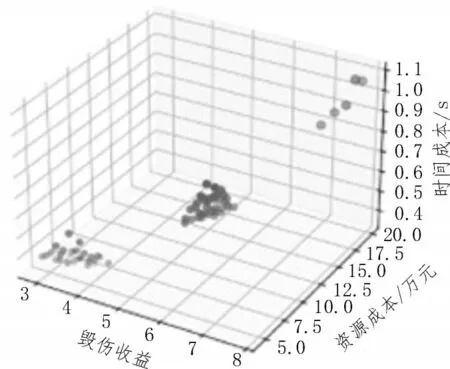
图3 R-NSGA-III

图4 NSGA-III

图5 R-NSGA-III
横向对比图2-3和图4-5可以看出,R-NSGA-III算法一方面可以根据决策者的偏好在相近区域提供更多解,而不是展示整个Pareto 最优前沿。另一方面偏好方案的区域是否有解也一目了然,可以让决策者对我方装备情况有额外的了解。
4.3 运行时间分析
在上述实验的基础上,该文又按照少打击目标、少武器型号、多武器数量这三种情况,额外进行了三组不同的实验来比较运算的时间开销,每组实验运行6 次取平均值。时间花费如表2 所示。

表2 运行时间对比
如表2所示,R-NSGA-III算法所花费的时间约为NSGA-III算法的52.05%。因此,可以验证R-NSGAIII 算法时间开销少,能够更快地辅助决策。
5 结论
针对常规导弹的特点,引入时间成本可以让决策者更详细地了解方案情况,直观地了解到偏好的指标是否有方案满足。有利于决策者选出适宜的方案,更好地达到辅助决策目的。并且R-NAGA-III 算法运行时间开销小,使得整体效率有大幅度的提升。综上,基于R-NSGA-III 的常规导弹火力分配辅助决策模型贴近实际作战,为智能决策提供有效的辅助支持,在对战决策场景具有重要的实际应用价值。
