基于子空间的可解释性多变量异常检测

宋润葵，郑扬飞，郭红钰，李 倩

(华北计算技术研究所 系统八部，北京 100083)

0 引言

异常检测是数据挖掘任务中的一种子类型，不同于其他的数据挖掘任务，比如聚类、分类等任务，异常检测针对的是少数的、罕见的、不确定的事件、对象。其应用领域十分广泛，比如计算机网络入侵检测[1]，银行欺诈[2]，医疗异常检测[3]，工业异常检测[4]等。由此可见针对异常检测算法的研究具有重要意义。在异常检测任务中，异常的种类通常有3种:点异常，条件异常，群体异常。按照数据类型划分有：统计性数据，如文本，网络流；序列型数据，如传感器数据；空间型数据，如图像，视频。本文主要针对的就是统计型数据上的点异常。

由于异常检测任务的特点，目前主要的研究都是针对于无监督异常检测的。目前国内外对异常检测的方法研究可以分成各种类型：比如有基于线性模型的，如主成分分析(PCA)[5]，最小协方差行列式(MCD)[6]，基于偏离的异常检测(LMDD)[7]；比如有基于衡量相似度的，如k最近邻居(kNN)[8]、AvgKNN[8]、MedKNN[8]，基于旋转的异常点检测(ROD)[9]；比如有衡量连接性的，如基于连接的异常点因子(COF)[10]；比如有衡量密度的，如局部异常因子(LOF)[11]；比如有概率方法，如基于角度的ABOD[12]； 比如基于神经网络的，如单目标对抗生成主动学习方法(SO_GALL)[13]，多目标对抗生成主动学习方法(MO_GALL)[13]，DeepSVDD[14]。这些方法都是在固定的全局特征空间上进行异常点挖掘的，此外这些方法都忽略掉了一个与异常点检测同等重要的问题，就是异常点解释。在许多应用场景中，用户更关心为什么检测到的异常点和其他的对象比起来是异常的。鉴于上述问题，本文的整体思路是在对子空间进行统计性检验处理的基础上，整合一个对象在多个子空间的异常值得分最终判断异常性，并提出关键子空间等概念，进一步对异常性加以解释。

1 在子空间中搜索异常点

1.1 相关概念与维度灾难问题

通常，异常检测的任务就是对于给定的数据集DB，计算出数据集中所有对象o的一个排名，用对象排名的先后来表示对象的异常性。数据集中的属性空间，即数据集中的所有属性组成的集合使用D来表示，其中D={0, 1, …,d-1}，总共d个属性。因此对象o的所有属性可以定义为o={o0,o1, …,od-1}。

假设使用rank函数来计算对象的异常值得分。一个理想的异常检测方法，应该使得一个异常点o和一个正常的对象p的异常值得分，rank(o)远小于rank(p)，这样才可以将异常点与其他对象显著区分开。而传统的一些方法可能会无法检测出一些隐藏在子空间中的异常点，因为rank(o)≈rank(p)。这一现象可以由这类数据集中存在分散的子空间来解释，对于每个对象而言只有部分属性子集是相关的，其余属性提供的或多或少是随机值。假如使用所有属性来计算对象之间的距离，就会出现维度灾难问题。下面简单阐述一下这个问题，现使用函数distanceD(o,p)来表示对象o，p在空间D上的距离，使用欧几里得距离来计算，如式(1)所示，其中变量i表示对空间D上的所有属性进行遍历：

(1)

随着空间D的属性数d增长，数据集DB中的对象o与其他对象之间的距离越来越相似，如式(2)所示。

(2)

因此在这样的全局空间中，对象距离变得没有意义，最终就会导致rank(o)≈rank(p)。

1.2 邻域N(o, S)的选择

在进行子空间选择之前，需要先介绍一个概念邻域N(o,S)，其中S表示一个子空间，意思是在子空间S内与对象o距离一定范围内所有其他对象的集合。即N(o,S)={p|distanceS(o,p)<ε(|S|)}。其中|S|表示子空间S的维度。ε(|S|)随着子空间的维度而变化。首先根据超球体的体积计算公式，可以得知d维子空间的体积公式如式(3)所示，其中ε可以理解为半径，在这里一般设置为0.5。Γ(·)是伽马函数，Γ(n+1)=n·Γ(n)，Γ(1)=1，Γ(1/2)=π1/2。

(3)

根据上述公式，进一步定义函数h(d)，如式(4)所示，其中n为数据集DB中数据的个数。

(4)

可以看出当n固定不变时候，h(d)函数是随着d单调递增的。在此基础上可以定义ε(|S|)，如式(5)所示，可以看出通过这样的设计，使得ε(|S|)在2维子空间以上，随着维度的增加而增加，这也为后续在多个不同维度的子空间中计算异常值得分做好铺垫。

(5)

当使用python来实现上述过程时，可以利用numpy包。使用numpy.sqart和numpy.sum函数来计算对象之间的距离，使用numpy.where函数来返回距离在ε(|S|)范围内的数据索引。

1.3 子空间的选择

为避免1.1节中提到的问题，在本节中将介绍如何为每一个对象选择出一系列的子空间，在这些子空间中，对象o和它的邻域N(o,S)有明显的区分性，规定使用RS(o)来表示这些子空间组成的集合。

首先，本文提出使用统计显著性测试来选择出需要的子空间S，进而组成RS(o)。因为对象是被分散的子空间所隐藏，所以此步的目的在于，通过在对象的邻域N(o,S)中测试数据的潜在分布，来排除掉均匀分布的子空间。如图 1给出的简单例子，子空间S={0,1,2,3}就是需要排除掉的子空间，在这样的子空间中，对象分布较为分散，几乎可以视为均匀分布，三角形和正方形表示的异常点被隐藏在其中，而子空间S={0,1}和子空间S={2,3}就可以很好的分别分辨出三角形和正方形表示的异常点，而子空间S={0}，这类稠密的子空间不会影响对异常值得分的计算所以不会被测试排除掉。具体的，在本文中采用的统计显著性测试方法为KS-检验。KS-检验可以用来测试两组数据有多大概率符合相同的分布，在这里用来判断给定的数据有多大概率符合均匀随机分布。

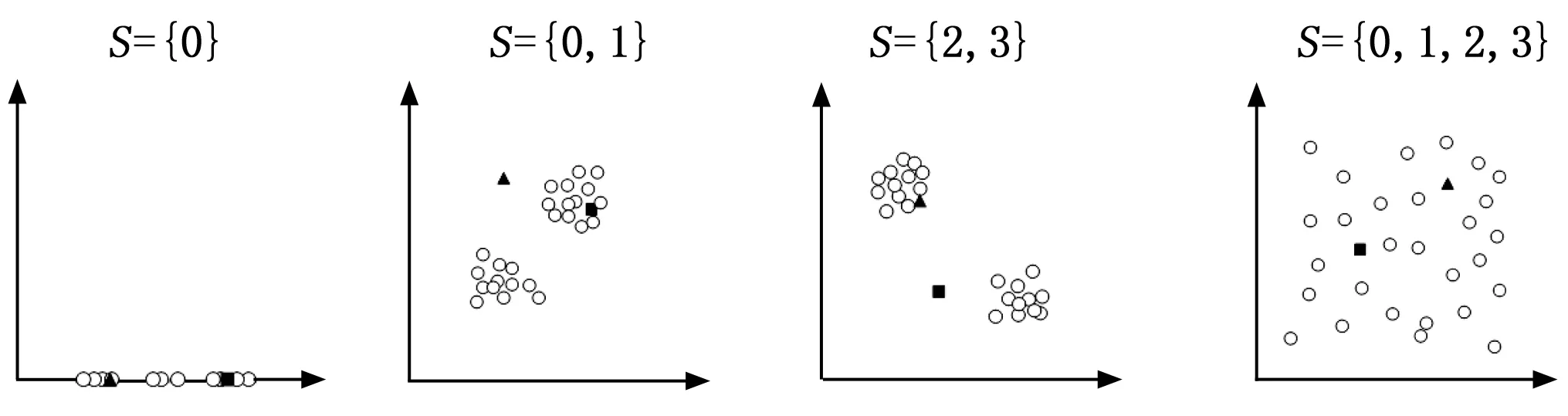
图1 不同子空间案例

具体而言，本文定义零假设H0：S在邻域N(o,S)中是随机均匀分布的。备择假设H1：S在邻域N(o,S)中是非均匀分布的。确保P(H0被拒绝|H0是真)≤α，其中α是显著性水平，一般设置为0.01。也就是说，拒绝H0的概率最大为1%，打个比方，在100个均匀分布的子空间中只有1个子空间可能会被判断为需要的子空间。

正如图 1中所展示的那样，随着子空间中包含的属性数量增加，逐渐成为了随机均匀分布的子空间，对象之间的距离逐渐变得相似。因此对子空间的选择就可以转变为对属性的选择，只要有均匀随机分布的属性被包含进这个子空间，就可以排除掉这个子空间。对于一个d维的全局空间D来说，它包含的非空子空间的个数为2d-1，也就是算法的搜索空间大小，由此可见，搜索空间随着维度的增加呈指数级增长，因此算法采用了增量处理和剪枝策略。如图2所示，从空集开始，每次添加一个属性进入子空间中，使用加粗字体表示新加入的属性，然后根据新加入的属性判断这个子空间是否是随机均匀分布的，在每次判断新的子空间时候，需要重新计算一次在这个子空间中对象o的邻域N(o,S)。图中箭头旁边给出的序号是算法的搜索顺序(为了增加图片的可读性，搜索顺序没有全部标出)，可以看出在这里采用了深度优先搜索，并且根据原始数据的属性顺序对属性进行编号，添加属性的时候按照编号升序的过程添加，避免了对相同属性构成的子空间的重复性搜索。至于剪枝策略，在搜索过程中，如果发现某个子空间是随机均匀分布的，则停止更深的搜索。

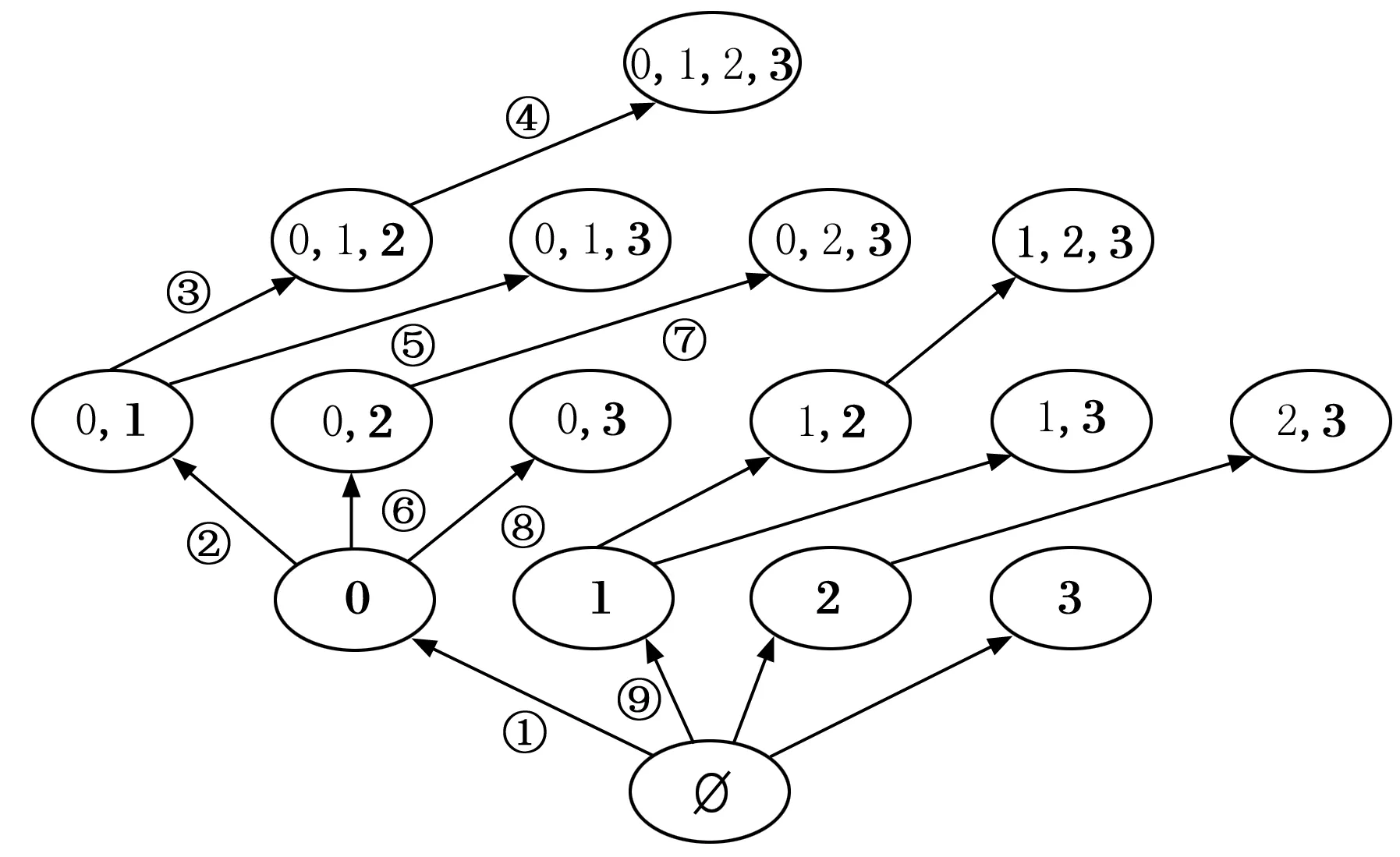
图2 子空间搜索策略

当使用python来实现上述的统计显著性测试时，只需使用scipy包中的stats.kstest函数，第一个参数为新添加的属性在邻域内对应的数据，第二个参数使用’uniform’，第三个参数使用(0,1)，所以需要确保输入的数据经过预处理后范围在0和1之间。

1.4 子空间中异常值得分的计算

本文中使用对象在子空间中的密度来评估对象的异常值得分，一个对象的低密度值会导致一个较低的异常值得分，也即是对象更为异常。因为对象可能会在多个不同的子空间中展开计算，所以需要设计一个在多个子空间中可比较的异常值计算方法。因为数据的整体密度分布是未知的，所以考虑使用核密度估计来估计对象o的密度den(o,S)。每个对象o对总体密度产生局部影响，使用核函数K(x)来定义这个局部影响，在这里采用Epanechnikov核函数，即K(x)=1-x2,x<1。核函数中的变量x=distanceS(o,p)/ε(|S|)，可以看出其为放缩后的对象o和对象p之间的距离。h函数如上文的式(4)所示，用来将每个对象o的影响放缩到最大距离。最终，如式(6)所示，对邻域内所有对象计算后求和，取均值。与简单的计算邻域内对象数量的方法相比，核密度估计方法对每个对象的影响进行了加权，ε(|S|)的存在使得为每个维度的子空间都选择了不同的带宽参数，增加了任意维度子空间下异常性的可比较性。直观来看，随着维度的增加，每个对象的影响也跟着增加，这可保证随着数据空间变得稀疏仍保持较优的密度估计。

(6)

当计算完对象o在不同的子空间下的den(o,S)以后，计算这些值的均值μ和标准差σ，然后找出那些den(o,S)<μ-2σ的。根据切比雪夫不等式可知，只有少数的对象会和均值差出两个标准差，这表示他们的异常性会比较高。关于对象o和均值μ，标准差σ的偏差按式(7)计算，可以看出一个对象o，如果它的密度与均值密度μ相比很低的话，dev(o,S)的值就会很高。

(7)

最终，对象o的单一子空间中异常值得分函数的定义如式(8)所示，可以看出整体上对象o的异常值得分函数实现了两个需求：第一是可以适应不同维度的子空间，第二是考虑到利用与均值的统计偏差来处理对象偏差。较低的密度和较高的偏差(即dev(o,S)≥1)都暗示对象有更高的异常性，即score_s(o，S)值更低。当偏差值小于1时，直接将异常值得分设为1，这样的设置有利于后续整合多个子空间下的异常值得分。

(8)

最终一个对象o的最终异常值得分可以按式(9)来计算。因为score_s(o,S)函数的范围是0到1，并且值越低表示对象的异常性越高，所以采用乘积的方式可以很好的让数值低的子空间对整体提供更大贡献，更加凸显异常点和正常对象之间的差异。

rank(o)=Πs∈RS(o)score_s(o,S)

(9)

1.5 算法整体流程

经过上文的详尽介绍之后，本节将在总体上对算法进行表述，代码风格参考了python代码，比如有关子空间的操作使用python中集合set的操作实现，对象数据，数据集等使用python中的ndarray数据结构进行操作。对于数据集DB中的每一个对象o都进行算法1的操作。算法2计算对象o，在所有通过测试的子空间的den(o,S)值。可以看出算法2使用递归的方式实现上文中的深度优先搜索以及剪枝策略。当得到所有对象的异常值得分后，按照值升序的顺序给对象进行排列，异常值得分越低代表对象越为异常，可以把异常值得分看作对象使异常点的概率值，也可以按照异常检测算法的常规处理方法，按照比例给对象赋予标签。

算法1：SMAD_o

输入：对象o，用o在数据集中的索引来表示；数据集X，即上文中经过处理后的数据集DB。

输出：对象o最终的异常值得分，即文中的rank(o)

1)初始化S=set()；

2)按照算法2计算，结果保存到all_den变量中；

3)计算均值μ和标准差σ；

4)按照式(7)计算；

5)按照式(8)计算；

6)按照式(9)计算；

算法2：den_o

输入：对象o，用o在数据集中的索引来表示；子空间S。

输出：所有通过测试的子空间的den(o,S)的结果

1)D_diff =D-S；

2)for i in D_diff:

(1)if(属性i的索引值小于子空间S中的索引值最大的属性)：

continue；按属性索引值升序处理，避免重复性的计算

(2)S_temp =S|i；

(3)根据1.2，1.3章节计算邻域N(o, S_temp)，并进行子空间测试；

(4)if(通过子空间测试)：

计算den(o, S_temp)；

调用算法2，参数o，S_temp；

else：

break

1.6 算法复杂度分析与优化实现

正如上文中提到的算法采用了剪枝策略，所以在这里主要分析的是最坏情况时间复杂度。首先对于每个对象o，都需要为其寻找子空间，当在最坏情况时，自下而上的剪枝策略没有发挥作用，此时所有的子空间都是非均匀分布的，这需要进行的子空间判断次数为2d。然后在计算密度的时候，产生了n次计算。最后，所有对象都需要进行上述步骤，总的来说的时间复杂度是O(2d·n2)。可以看出最坏情况的总体时间复杂度，一部分是指数级的，一部分是平方级的，所以下面提出了进一步的算法实现优化。

对于一个对象o而言，在式(6)的计算过程中，在多个子空间中会发生重复的距离计算，所以可以把欧几里得距离计算步骤中的，求差值和求平方的过程提前到算法1的步骤(2)的前面，并把结果作为参数传入算法2。对于n个对象的处理而言，可以看出对象和对象的处理之间是没有数据交换的，只有在最后的阶段需要根据所有对象的异常值得分进行排序，因此可以采用同步并行算法。使用python编程时，可以使用multiprocess包，它是一个基于进程的并发程序包，可以最大程度利用处理器的多线程处理能力。一个简单的实现方法就是直接实例化一个Pool对象，初始化参数使用os.cpu_count()，按照计算机的处理器数量来生成并发池中的进程。这个函数提供了一种简单的实现数据并行的方法，利用starmap函数可以将多个输入变量传入函数中，使得同一时间有多个相同的函数传入了不同的参数在不同进程中处理。调用close()和join()函数，当所有任务完成后，并行自动退出，然后即可进行后续的异常对象排序。对于，时间复杂度随着维度d而指数级增长的现象，结合集成学习的方法，对全局空间做无放回的随机采样，先生成若干个小规模的空间，然后把这几个小规模的空间交给算法独立处理，结果同样按照式(9)的思想进行乘积结合。

2 基于子空间的可解释性

2.1 概念提出

在上文的子空间概念的基础上，在本节研究可解释性。因为上文中异常点的判断是综合多个子空间后的结果，所以在这里需要先明确对象o是子空间S的异常点这一概念。参照图 2把不同维度的子空间看作一层L，规定层数自底向上递增，即L0,L1…。因为在上文中对每个对象都选取了合适的子空间，并计算了score(o,S)，此时在每个子空间下，对属于该子空间的score(o,S)进行升序排序，摘取排在前面的10%的对象组成集合，并与算法1中步骤6输出的结果前10%的对象组成的集合做交集运算，运算结果中的对象即可视为这个子空间S的异常点。在此定义的基础上，下面提出一些相关概念。

特殊异常点：假设对象o是子空间S的一个异常点，如果在S的任何一个子集里，对象o都不是异常点，则o是S中的特殊异常点。强异常点：如果子空间S包含一个或更多的异常点，而在S的任何子集里都没有异常点存在，则称子空间S为强异常空间，此时S中的任何异常点o都叫做强异常点。从定义中可以看出强异常点一定是特殊异常点。弱异常点：如果对象o是子空间S里的一个特殊异常点，如果o不是最强异常点，则o是一个弱异常点。可以看出，特殊异常点专注于对单一对象的解释，利用最小的属性子空间来解释对象的异常。强异常点和弱异常点的概念更关注异常点之间的关系。强异常空间是较为重要的概念，因为它的子集都不包含异常点。

利用上述概念，便可以很好的增强算法结果的可解释性。比如为每个异常点找到合适的子空间使其在那个子空间下成为特殊异常点。强异常空间，从低到高层来看是首个包含异常点的子空间，所以它和强异常点可以体现更为关键的异常情况。强异常点和弱异常点放在一起可以解释异常点之间存在的某些关系。

2.2 基于子空间的可解释性算法流程

为了减少算法的重复性计算，改善算法的效率，可以在算法1中的步骤(6)后把对象o在每个子空间S中的score(o,S)暂存起来。以子空间为单位，把属于这个子空间的异常点都放一个集合中o_set。以子空间维度升序进行排序并放入列表L中。对于算法1中检测出的每个异常点，在排序好的子空间序列L上从前到后的进行搜索，当在一个子空间对应的集合o_set中搜索到这个异常点后，即可认定这个异常点在当前子空间下是特殊异常点。

对于强异常点的计算，同样在L上，从前向后遍历每次取出一个子空间S，判断其真子集是否在L中。由数据结构可知判断过程只需向前搜索，每次对比的子空间为S_t，以python代码风格来表示，需要判断S_t&S是否与S_t相同，如果相同说明S_t是的S真子集。经过判断后如果没有真子集，则S是强异常空间。然后移除这个S的所有超集，可以直接使用issuperset()函数来判断超集。继续取下一个子空间S，重复上述过程，直到L遍历完成。

对于弱异常点的计算，由定义可知，从特殊异常点中刨除强异常点就可得到弱异常点。即，由特殊异常点构成的集合，与强异常点构成的集合做差集，剩下的异常点就是对应子空间的弱异常点。

2.3 可解释性算法的可扩展性与非侵入性

上文中已经讲述了特殊异常点，强异常点，弱异常点的概念，并介绍了算法的主体思想，即按维度升序来对每一个子空间做处理。上述概念与算法思想可以轻松的扩展与移植到其他的算法之中，非侵入性是指对原始算法不产生其他影响，只作为附加算法，增加一些附加步骤，来增强结果的可解释性。

对于一种异常检测算法M，可以先在全局属性空间计算异常点，将结果组成集合R_set，然后再对全局空间划分成不同维度的属性子空间，同样以维度升序的方式，在每个子空间执行算法M，都生成了一个结果集合r_set，对R_set和r_set做交集运算，其结果作为当前子空间的最终的异常点检测结果。然后同样可以按照2.2章节来算出特殊异常点，强异常点和弱异常点。

3 实验

3.1 实验平台软硬件条件

本章节全部实验的运行环境为win10操作系统，CPU是i7-6700HQ，内存16 GB，IDE使用PyCharm2021.2.1，python版本号3.8.5，主要使用的python包有：numpy 1.19.5；pandas 1.2.2；scipy 1.6.2；scikit-learn 0.24.1。

3.2 评价指标

异常检测问题可以看作为一种特殊的二分类问题，所以本文中使用广泛使用的AUC，P来评价算法的有效性。AUC即ROC曲线(接受者操作特征曲线)与x轴和y轴围成的面积，P即查准率或精度。在介绍这两个指标之前需要先介绍一下如表 1所示的混淆矩阵。在做异常检测时候，可以把异常点当作正例，把其他点当作反例。

表1 混淆矩阵

在混淆矩阵的基础上，可以得到查准率P的定义，如式(10)所示，可见P值越高越好，理想状态下，最佳时候为1。

(10)

ROC曲线的纵轴是TPR(真正例率)，横轴是FPR(假正例率)，分别如式(11)和(12)所示。在此基础上，即可绘制出ROC曲线，理想状态下，TPR高，说明异常点被漏检的少；FPR低，说明被误认为是异常点的少，AUC值趋近于1。

(11)

(12)

3.3 数据集选取

实验采用的数据集来源为ODDS[15]，ODDS的数据集主要是在UCI[16]中的分类任务用数据集的基础上对数据的标签做了处理，将标签中的少数类标记成异常点，并把数据集封装成mat类型文件，使用X变量来表示对象的各维度的数据，使用y变量表示对象的标签，方便异常检测任务的直接使用。下面选取了ODDS网站中的13个多维点异常数据集，这些数据集来源于多个不同的应用领域，比如医疗领域的数据集：annthyroid，Arrhythmia，breastw，cardio，lympho，pima，vertebral分别是甲状腺疾病，心律不齐，乳腺癌疾病心电图淋巴管造影术糖尿病和脊柱的数据，此外还有雷达数据，玻璃数据，红酒数据等。数据集的基本情况如表2所示，可以看出选取的数据集样本个数，数据维度，异常点比例变化范围很广。异常点比例将应用于给异常点打标签进而计算查准率。

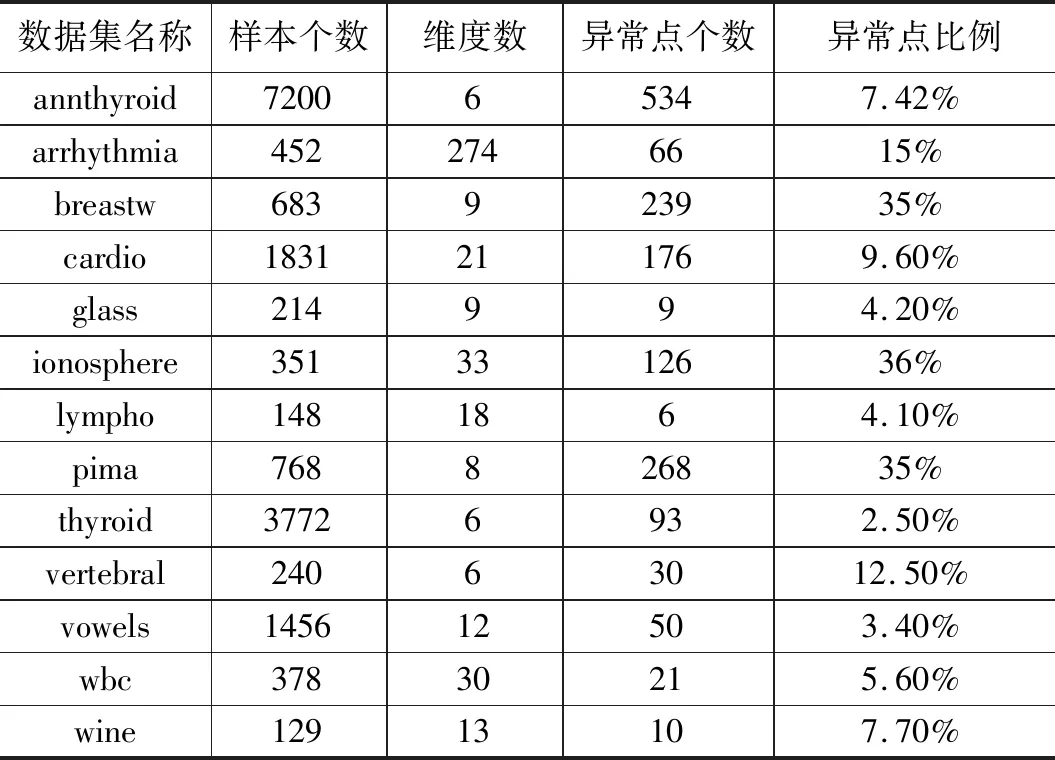
表2 数据集信息

3.4 对比方法设置

本文选取了10种不同类型的对比方法，按照方法英文缩写名升序排序分别是ABOD、CBLOF[17]、DeepSVDD、FB[18]、HBOS[19]、LODA[20]、LOF、MO_GALL、ROD、SO_GALL。上述对比方法的主要实现来源于赵等人的文章[21]。

ABOD方法是指基于角度的异常检测，其把一个对象关于所有邻居的加权余弦值的方差作为异常值得分，方法包含一个超参数邻居个数，在这里设置为10。CBLOF方法是基于聚类的异常点检测，在这里使用KMeans聚类方法，聚簇数设置为8，α和β参数分别设置为0.9和5，用来划分大、小聚簇，然后根据对象所在聚簇的大小和其离最近的大聚簇的距离来评估异常性。DeepSVDD方法是一个深度方法，使用了自动编码器，程序的基本参数设置如下，隐藏层神经元个数64，32，隐藏层激活函数relu，输出层激活函数sigmoid，优化器选择adam，迭代次数100，批大小设置32，丢弃概率0.2。HBOS即基于箱线图的异常检测，参数设置如下：桶的个数设置为10，α设置为0.1，tol设置为0.5。LOF方法参数设置如下：邻居数量设置为20，采用欧式距离。FB是指feature bagging，使用多个基检测器在数据集的子集上进行检测，并取平均值，参数设置上，选择LOF作为基检测器，检测器数量10。LODA是轻量化在线异常检测方法，参数设置如下：桶的个数设置为10，随机划分的数量设置为100。MO_GALL参数设置如下：子生成器个数10，迭代次数20，生成器学习率0.000 1，鉴别器学习率0.01。SO_GALL参数设置如下：迭代次数20，生成器学习率0.000 1，鉴别器学习率0.01。

3.5 实验设计与结果分析

实验开始前，需要对输入数据做预处理，预处理方法选用sklearn.preprocessing.MinMaxScaler函数，将数据范围调整到0和1之间，并保持数据的形状与原数据一致。每个算法在每个数据集上运行10次，再取平均值作为最终结果。如表3给出的是本文方法SMAD与其他10种方法在13个数据集上的AUC，并在下方给出了每个方法在多个数据集上的平均AUC，使用加粗字体表示在该数据集上的最佳结果。可以看出本文方法SMAD在部分数据集上结果是最佳的，在其他数据集上结果没有太大劣势，这类数据集的一个特点是异常点比例偏低。从总体上看，本文方法在平均AUC上最高的，可见对子空间进行选择这一过程产生了实质性效果。表 4中给出了不同算法在数据集上的查准率的对比，给出了每个方法在数据级上的平均查准率，并用加粗字体表示该数据集上的最优结果。可以看出，总体上与表3体现出了相似的结果，本文方法在平均查准率上是最佳的，在低异常点个数的数据集上算法的查准率相对来说都会变差，尤其是几个深度学习方法劣势较为明显。表5给出了不同算法在数据集上的运行时间对比结果，以及在每个数据集上不同算法的平均运行时间，并用加粗字体标记出运行时间最长的算法。从表格结果可以看出本文算法的运行时间介于其他几个机器学习算法和以DeepSVDD为代表的深度学习方法之间。子空间的搜索过程给算法的整体运行时间带来了一定的负面影响，尤其是在数据维度很高的时候，运行时间会较为明显的增加，不过与深度学习这类方法相比，本文算法的计算过程还是相对较为简单的。此外受制于实验平台的CPU物理核数影响，算法的并行实现没有带来较为明显的运行时间的改善。

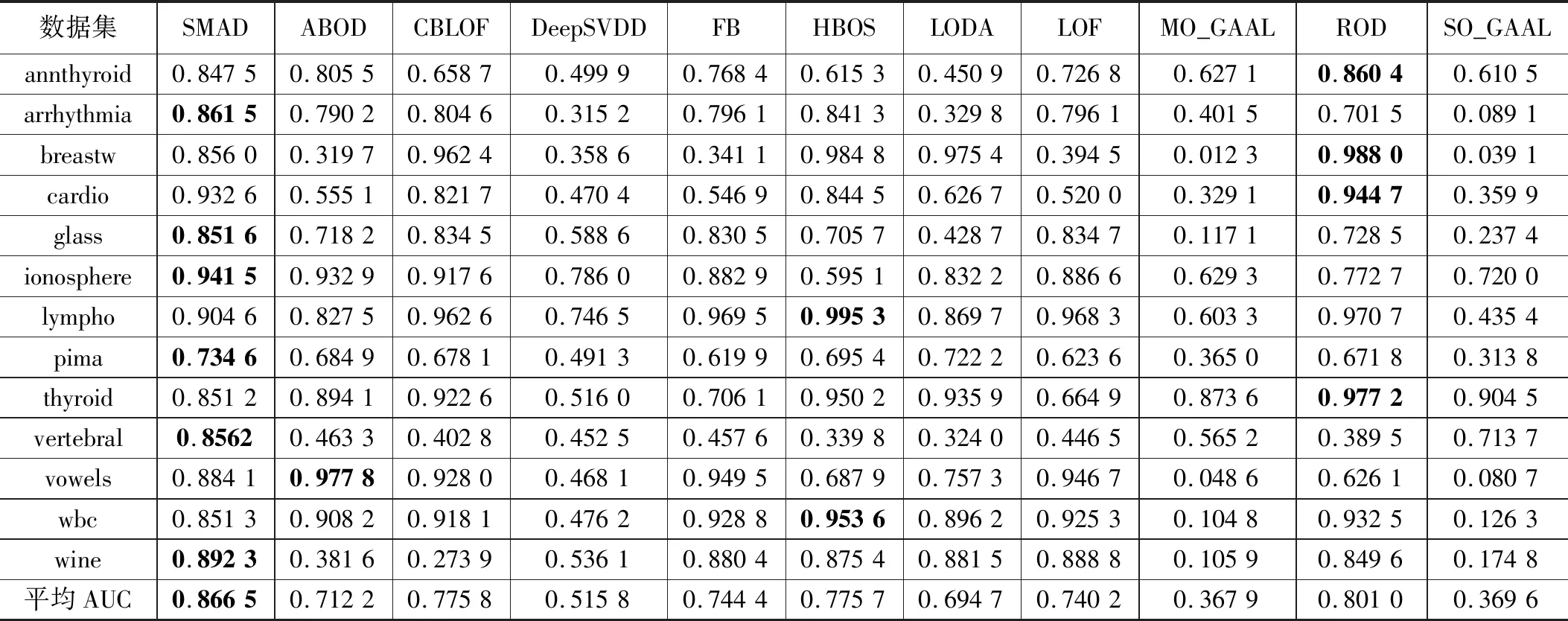
表3 不同算法在数据集上的AUC对比结果

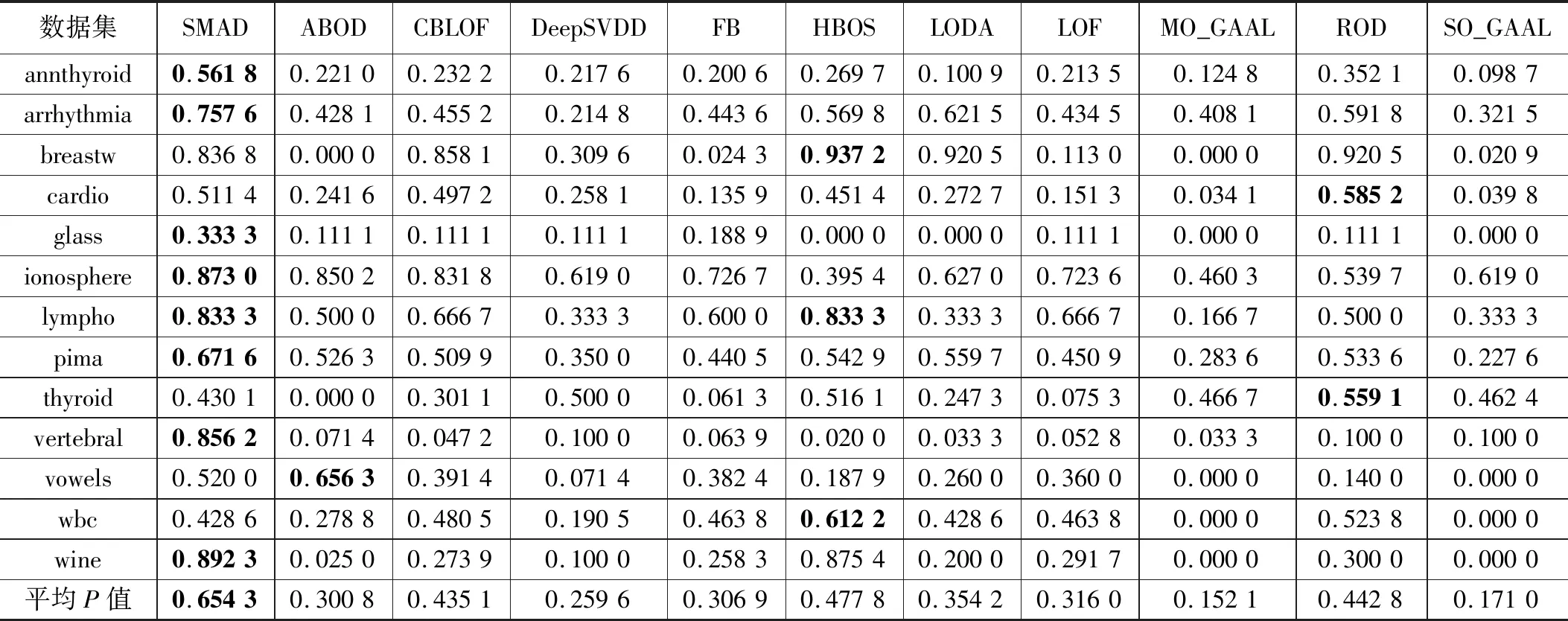
表4 不同算法在数据集上的P值对比结果

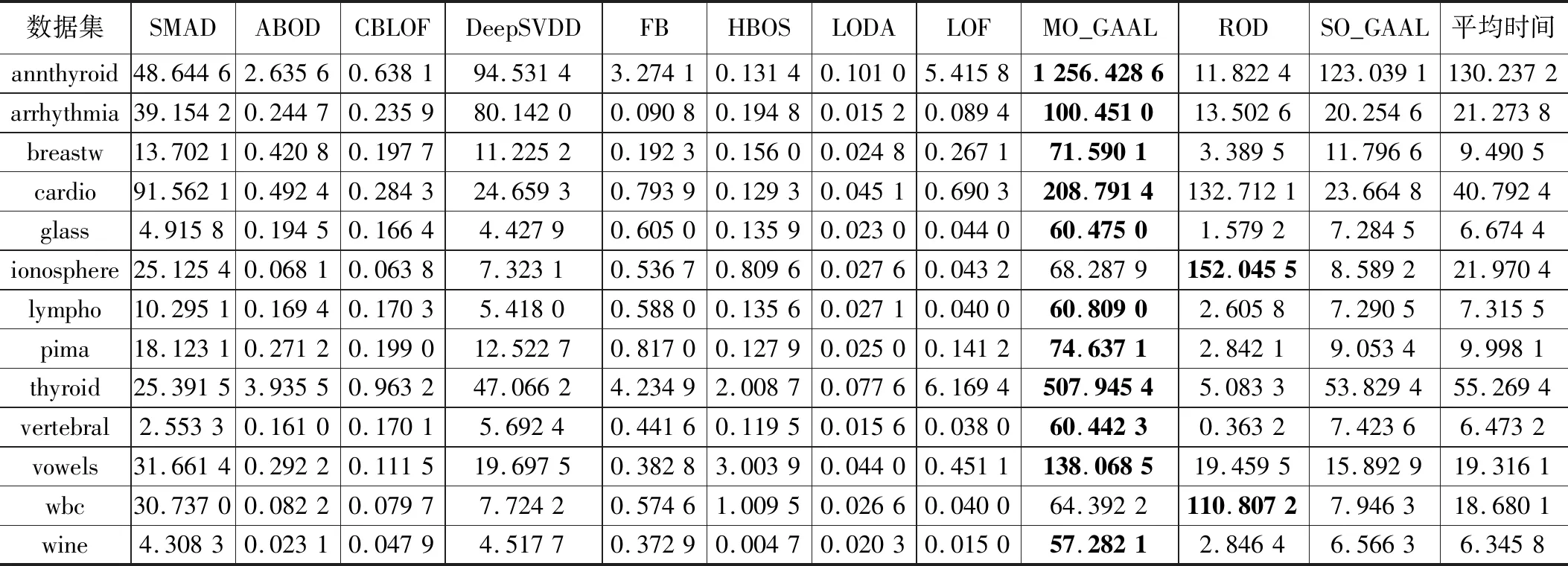
表5 不同算法在数据集上的运行时间对比结果

综合表 3、表 4和表 5实验结果，以及考虑到算法的无参数特性，可以确定本文提出的算法在实际应用场景中适合在周期性的数据批处理过程中使用。

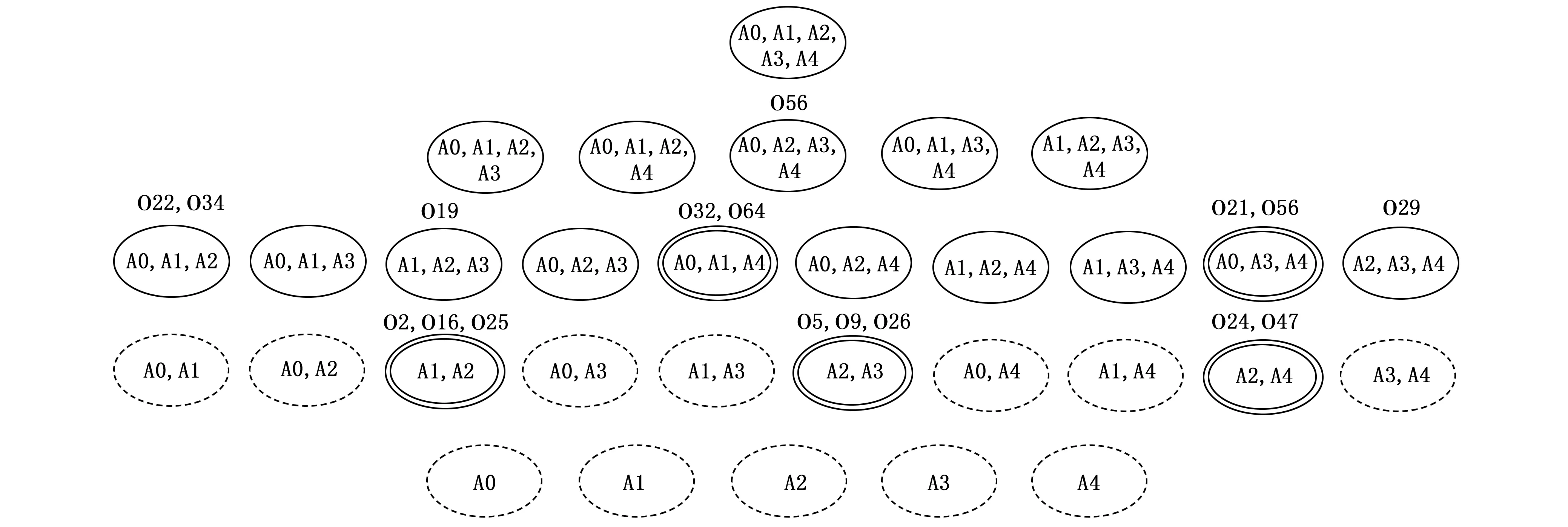
图4 可解释性图例

因为AUC相比查准率可以更好的评估算法的综合性能，为了更好的展示本文算法的优势，图 3以折线图的方式给出了这11中方法在这13个数据集上的AUC结果。可以看出本文的算法的折线基本集中在上方，可见其有效性。

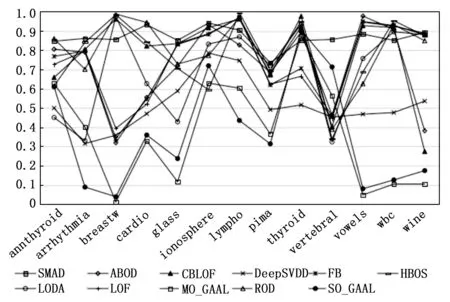
图3 不同算法在数据集上的AUC折线图

3.6 可解释性算法结果展示

在这一章节中，使用ionosphere数据集来呈现可解释性算法的结果。ionosphere数据集是来自于拉布拉多鹅湾的一个雷达系统的数据。其有17个脉冲数，每个脉冲数使用2个属性来表示，对应于由复杂电磁信号产生的函数返回的复数值，一共34个属性，其中一个属性的数据是全0的，所以舍弃掉该属性，剩余33个属性。为了展示的简洁性，图 4以树形图的方式展示了在部分属性上的部分对象的结果，使用椭圆表示一个子空间，A0～A4表示5个属性，虚线的椭圆表示该子空间不包含任何异常点，双实线的椭圆表示该子空间是强异常空间，单实线的子空间表示该子空间不包含强异常点，但可能包含弱异常点。椭圆上方用字母‘O’加数字的形式表示在该子空间下发现的异常点，根据第2章节的讲解，可知双实线椭圆上方标出的是强异常点，单实线椭圆上方标出的是弱异常点，可见这一形式可以很好的改善用户对异常点之所以异常的理解。

4 结束语

针对多维特征数据中，部分异常点被分散的特征空间所掩盖而无法检出的问题，以及当前方法可解释性不佳的情况，本文提出了基于子空间选择的异常检测算法。利用统计性检验选择子空间，结合多个子空间的结果作为最终的异常值，并在子空间的基础上提出了对异常点的解释方法。在公开数据集上的测试展现了算法较佳的检测性能。在未来的研究中，将进一步针对算法的执行效率进行优化，如引入VP树等数据结构来加快搜索速度。