一种改进的自适应多元变分模态分解轴承故障信号特征提取方法

时培明, 张慧超, 伊思颖, 韩东颖

(1.燕山大学 河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004;2.燕山大学 车辆与能源学院,河北 秦皇岛 066004)

1 引 言

大型低速重载机械关键部件极易损坏,使得机械故障的发生具有不可预测性,危害极大。调查数据[1]显示,轴承故障占所有变速箱损坏的64%,轴向裂纹占所有轴承故障类型的71%,由此可见研究先进的轴承故障诊断算法的重要性,以及保证设备正常运行的实际意义。但该类设备的故障信号具有能量低、周期长、断层信息极微弱、易受背景噪声干扰等特性,使得故障特征的提取难度大大增加。

根据参考文献[2,3]关于故障诊断技术的综述可知,旋转机械振动信号具有明显的非线性非平稳特性。经典的信号处理方法包括短时傅里叶变换、小波变换S变换、经验模态分解(empirical mode decomposition, EMD)[4]、集成经验模态分解(ensemble empirical mode decomposition, EEMD)[5]、二元经验模态分解(Bidimensional empirical mode decomposition, BEMD)[6],多元经验模态分解(multivariate empirical mode decomposition, MEMD)[7]等。

但以上方法具有一定的局限性,许多学者在上述方法的基础上提出了改进方案,如：汪朝海等人将EMD与主成分分析相结合,用于滚动轴承的故障诊断研究[8]；李继猛等人将集成经验模态分解与K-奇异值分解相结合用于故障诊断,取得了一定的效果,并在机械的故障诊断中得到了实际应用[9]。然而,由于理论框架的局限,所提出的改进只能在一定程度上对已有缺点进行压制,不能从根本上消除。

2014年Dragomiretskiy K等提出变分模态分解算法(variational mode decomposition, VMD)[10]。它是一种处理非线性非平稳振动信号的方法,其核心算法是将希尔伯特变换和维纳滤波相结合,通过迭代求解变分问题。该算法有深厚的数学理论基础,从根本上克服了端部效应、模式混叠等问题,在机械故障诊断等领域有广泛应用；多元变分模态分解(multivariate variational mode decomposition, MVMD)是VMD算法在多变量或多通道数据集上的一般推广[11]。该算法信号分解过程基于所有通道数据间存在共同频率分量,通过构造变分优化问题来提取多变量输入信号中固有的多变量调制振荡带限模式集合,其分解过程中的影响参数与VMD相同,都与本征模态数k、二次惩罚因子α、更新参数ζ和收敛容差参数ε有关。此外,这些参数必须预置,需要高度经验,不适合作为实际工程应用中的自适应模型。因此,自适应多元变分模态分解是一个新的研究方向。苏晓等提出基于VMD和变尺度随机共振降噪算法,用于微弱信号的故障特征提取[12]；吕蒙等提出一种改进的VMD算法,并应用在滚动轴承诊断上[13]；李永帅等人将VMD与K-SVD相结合应用于管道泄漏振动信号的处理上[14]。目前,对MVMD参数设置研究较少,Gavas R等将MVMD用于脑电信号的眨眼去除处理,但在算法本身没有进行优化,只是在电脑方面的一个应用[15]。

为了更好地提取滚动轴承的故障特征,本文提出一种自适应多元变分模态分解算法,用来提取滚动轴承的故障特征,通过与其他方法的对比实验,验证本文所提方法的实用性和高效性。

2 算法理论基础

MVMD算法广泛应用于脑电、旋转机械等多个领域,但就目前来看,主要存在2个问题：(1)在信号分解中,主要参数的选择是根据以往经验设定,这使分解的结果具有一定的局限性；(2)由于工业生产环境的不确定性,使得原始采集数据包含许多噪声干扰,利用算法分解所得的模态分量中含有小幅值的同频段嘈杂噪声的干扰,妨碍特征信息的识别。针对以上所述问题,本文提出一种新的信号分解方法,即自适应多元变分模态分解算法。

2.1 多元变分模态分解(MVMD)

自适应多元变分模态分解是在MVMD的基础上提出的,目的在于解决MVMD人为参数设置对分解结果准确度的影响,其分解效果主要受2个参数的影响：本征模态数k和惩罚参数α,该算法的核心思想是构建求解模态的变分问题。首先定义1个所有输入数据通道之间存在共同分量的多变量调制振荡模型,为了提取多变量输入信号中固有多变量调制振荡的有限带宽模态集合,将其构造成1个变分优化问题,通过交替方向乘子法来实现变分模态的最小化,从而得到在多变量调制振荡的所有通道中共同存在相同中心频率的多变量模态的最佳集合。

将多通道原始信号同时分解为k个模态分量,并保证分解序列为具有相同中心频率的有限带宽信号,同时各模态的估计带宽之和最小,相应的约束变分优化问题表达式为：

(1)

式中：C表示通道的个数；k表示信号分解的模态个数；uk,c为第c通道的第k个模态；ωk表示k个模态的中心频率。

然后,构建1个增广拉格朗日函数,将式(1)引入拉格朗日乘法算子,使式(1)由约束问题转变成非约束问题,在拉格朗日函数中增加了两个惩罚项：1个是用于加强重建保真度的二次项,另1个是具有拉格朗日乘子λ的项,以确保严格满足约束条件。相应的表达式为：

L({uk,c, {ωk},λc)=

(2)

以上非约束问题可以通过交替方向乘子法来解决,随后的模态更新、中心频率更新和拉格朗日乘法算子的更新如下：

(3)

(4)

(5)

关于多元变分模态的分解算法的详细内容可以参考文献[9]。

2.2 混合灰狼优化算法

混合灰狼优化算法(hybridizing grey wolf optimization, HGWO)是一种改进的灰狼算法[16]。它利用差分进化算法的特点来生成初始种群,提高了全局搜索能力和灰狼算法的计算精度,原始灰狼算法的本质是模拟灰狼寻找猎物的行为来搜索最优解。

由于狼群中存在社会等级,在算法的迭代过程中,根据适应度从大到小划分为4个等级,即(α、β、γ、ω),目标函数的最优解将依次由α、β、γ来定位,ω将计算自己与猎物之间的距离,最终,狼群通过式(6)、式(7)和式(8)不断更新和进化,逐渐缩短自己与猎物的距离,从而实现捕猎。

Dα=|C1·Xα-X|
Dβ=|C2·Xβ-X|
Dδ=|C3·Xδ-X|

(6)

X1=Xα-A1·(Dα)
X2=Xβ-A2·(Dβ)
X3=Xδ-A3·(Dδ)

(7)

(8)

2.3 最小模态重叠分量

为了克服MVMD在信号分解时参数设置方面的缺点,本文提出一种新指标来对分解效果进行定量的评估,即最小模态重叠分量(minimum mode overlap component,MMOC),用它作为优化算法的适应度函数来寻求最优解。

首先,需要介绍的是模态重叠分量(mode overlap component, MOC),其详细的公示表达如下：

(9)

(10)

式中：OAi表示相邻模态IMFi和IMFi+1频域部分重叠的部分,其中,ui(ω)表示IMFi的各个频域点,ui+1(ω)表示IMFi+1的各个频域点；max()和min()分别表示对应模态频域的最大值和最小值,其物理意义解释见图1,红色箭头指向的椭圆中为相邻模态分量IMF1和IMF2的重叠区域。

图1 频域重叠图Fig.1 Spectrum overlap chart

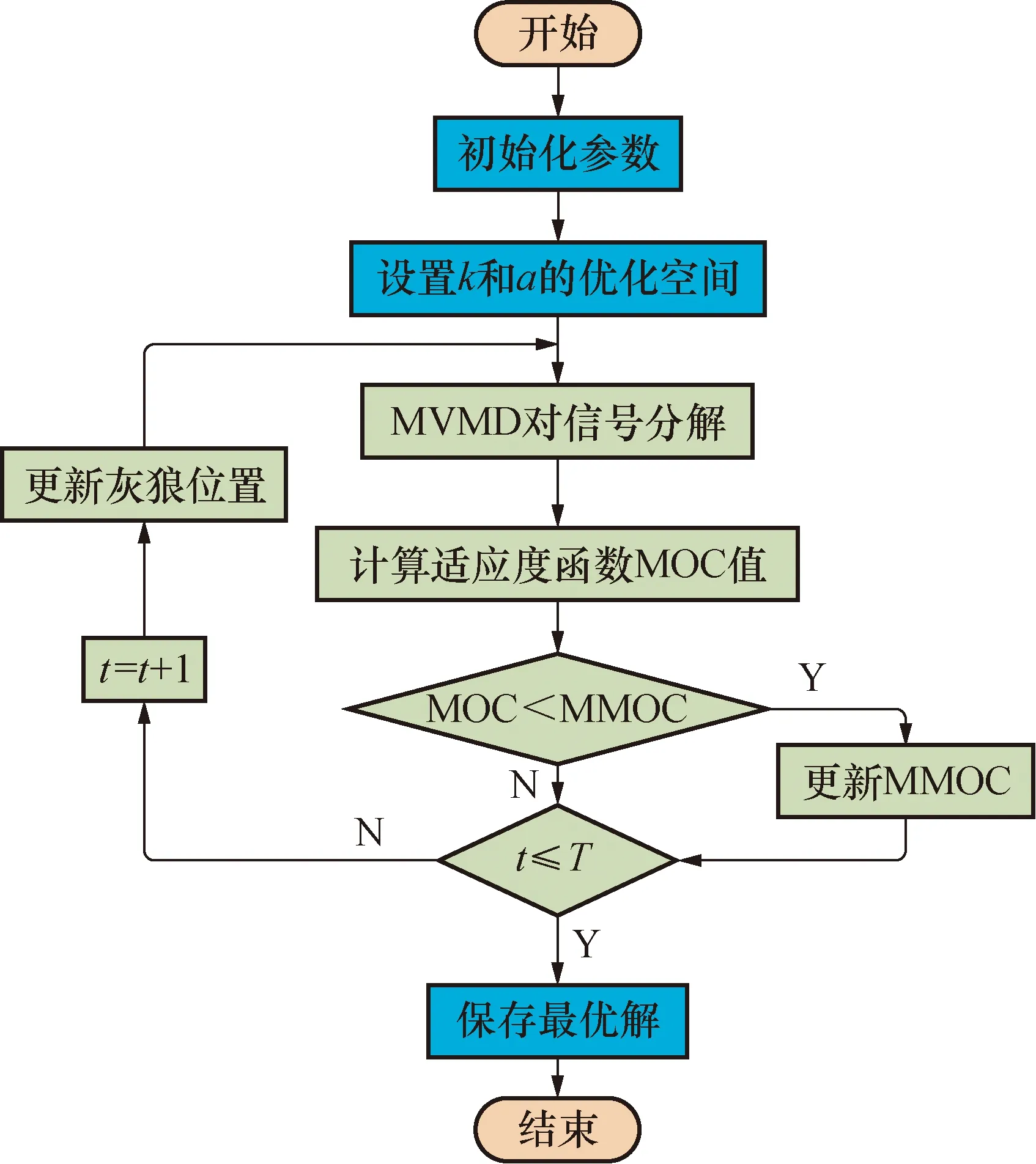
详细模态重叠分量伪代码实现过程如下,将模态重叠分量设为适应度函数,当该指标取到最小值时,各个模态分量间独立性最强,相关性最小,则对应的优化参数为最优解,MVMD将按照最优参数值对原始信号进行分解,获取多个模态分量,从而为实现自适应多元变分模态分解提供理论基础和依据。

模态重叠分量计算过程：

初始化：OA=0

j=0

更新：Fori=1:K

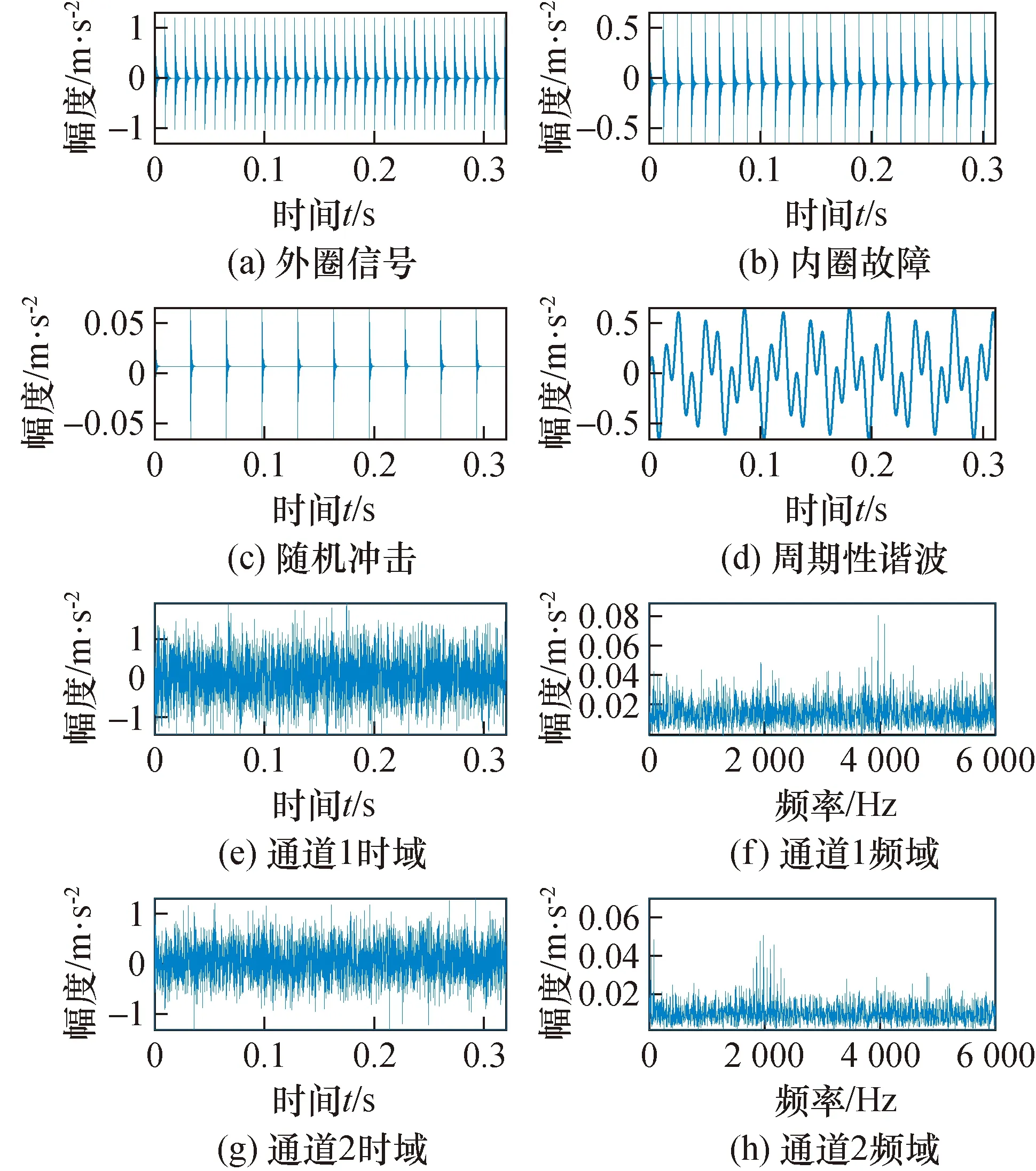
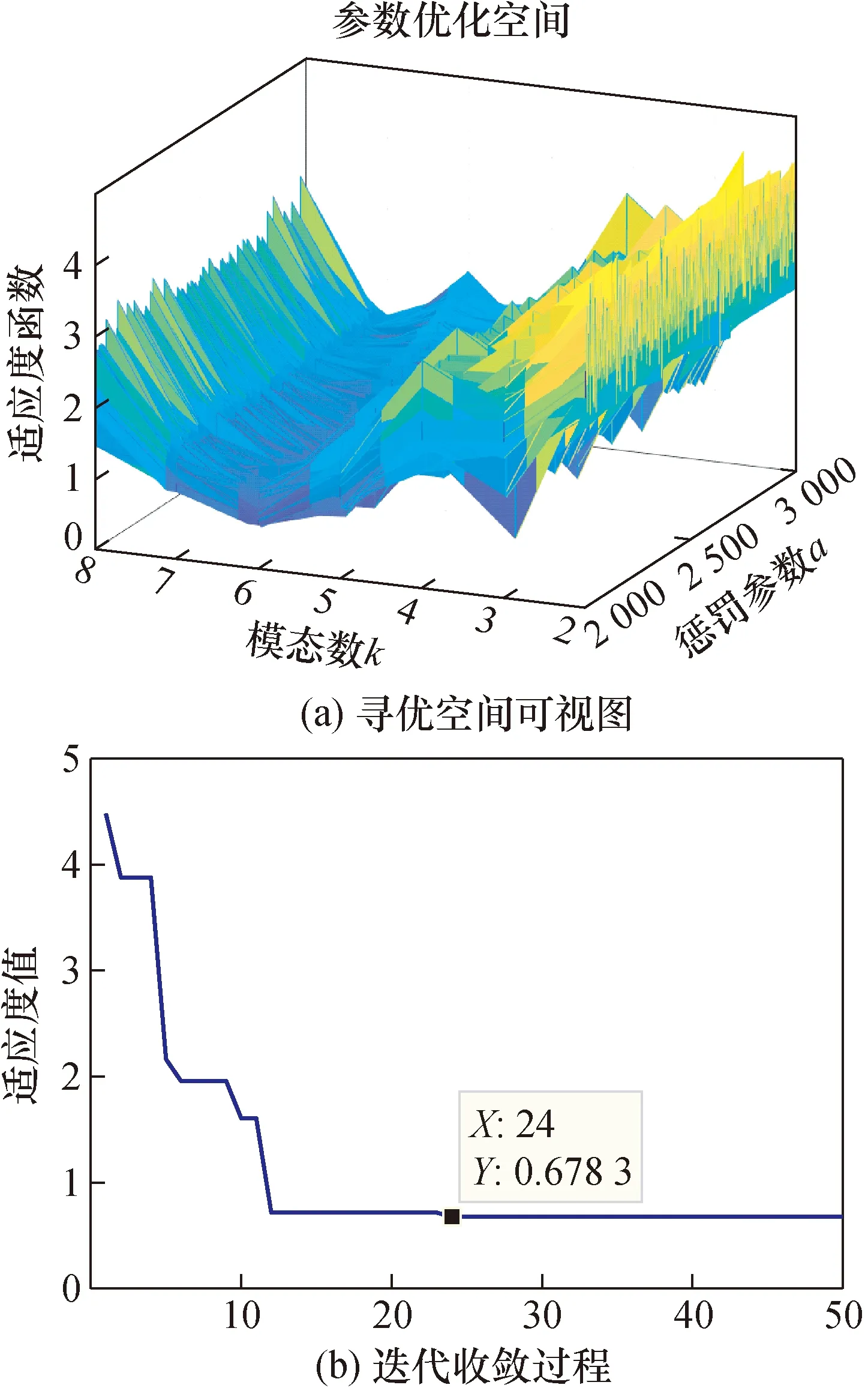
If minui+1

OAi=IMFOi

OA=OA+OAi

j=j+1

else:

OAi=0

OA+=OAi

end

重叠分量：MOC=OA·j-1

3 自适应多元变分模态分解

自适应多元变分模态分解(adaptive multivariate variational mode decomposition, AMVMD)是将HGWO算法应用到多元变分模态的参数寻优上,不仅可以解决人为经验参数设置的不准确性,更大意义上使算法可以根据信号本身的特征对参数进行设置,获得最佳分解效果。具体的算法流程见图2。

图2 AMVMD算法流程图Fig.2 AMVMD algorithm flow chart

首先需要初始化HGWO的各个参数,包括狼群个数、最大迭代次数、自变量维数、缩放因子上界和下界、交叉概率以及优化参数的上界和下界；然后,计算适应度函数,即模态重叠分量,更新狼群位置,再次计算适应度函数并进行比较得到最小值保存；进入下1次迭代过程；最后,满足以下2个条件之一则算法结束：①未达到最大迭代次数,找到全局最优解；②到达最大迭代次数,保存最小值结束。

4 仿真数据

对于具有局部故障的机械振动信号,除了故障分量和噪声外,还可能存在由轴承旋转或齿轮啮合引起的随机冲击和周期性谐波。这里对滚动轴承的故障信号进行公式拟合,详细见式(11)：

(11)

式中：A,B,R,P为不同项振动幅值；T为2个相邻脉冲之间的时间间隔；轴承打滑造成的时间延迟为τ；fh表示谐波干扰频率。

脉冲响应函数见式(12), 其中β和fn分别表示阻尼系数和谐振频率。

通常,外圈故障幅值不变A为常数,内圈故障幅值B表达式见式(13),其中b为振幅,fr为频率。

式(11)～式(13)中的φ均表示相位。

x(t)=e-βtsin(2π fnt+φ)

(12)

B=1+b·cos(2π frt+φ)

(13)

在该仿真实验中,噪声采用的是SNR=5 dB的高斯噪声,上述公式中的相位均为0,频率fr为 30 Hz,外圈和内圈的故障频率fo和fi分别为80 Hz和110 Hz, 外圈故障、内圈故障和随机冲击的谐振频率分别设置为3 000、4 000、4 500 Hz,阻尼系数分别为1 000、1 200、1 500,幅值A和B分别为0.86、1.3,τi和τj分别为0.01T0、0.01Ti；R和Tr由MATLAB中0～1的随机数产生,第四部分周期性谐波的表达式为0.01×sin(20π t)cos(60π t),仿真信号中外圈故障、内圈故障、随机冲击和周期谐波见图3(a)～图3(d),将外圈信号、随机冲击、周期性谐波和噪声合成的信号见图3(e)设置为通道1的输入信号,将除外圈以外的信号见图3(f)设置为通道2的信号,其中噪声的信噪比为5 dB。用文中所提算法进行特征提取,同时设置对比实验来验证所提算法的优越性。

图3 仿真信号Fig.3 simulation signal

首先,采用所提算法对上述仿真信号进行分解,优化算法的初始化参数设置见表1,寻优过程中的空间图和迭代过程见图4。

图4 参数优化过程图Fig.4 Parameter optimization process diagram

通过图4(a)可以看出模态数在2～6之间,适应度值在逐渐减小,此时信号处于欠分解状态；当模态数大于6时,原始信号分解过度相邻模态间的重叠面积增大,使得适应度值不断增大。由图4(b)算法的迭代收敛过程可知,当进行第24次迭代时,适应度值取到最小为0.678 3,此时的优化参数最佳,模态数k为6,惩罚参数为2 487, MVMD将按照最佳参数对仿真信号进行分解,所得的模态分量的时频域见图5。

表1 优化算法参数设置Tab.1 Optimized algorithm parameter Settings

图5 仿真信号对比结果Fig.5 Simulation signal comparison results

由于MEMD分解算法应用于3通道及以上信号,因此该部分的对比实验采用的是BEMD算法,BEMD算法继承EMD算法本身的特点,可以对信号进行自适应分解,分解结果分为模态分量和信号残差两部分,模态分量的时频域图见图5所示,由于空间有限在对比图中已将残差信号省略。

图5为2种算法信号分解时频域的对比结果图,图5(a)为所提算法仿真信号的时域图,周期性信号被清晰识别,结合图5(c)对应的频域分析可以看出在IMF1中外圈故障特征和内圈故障特征被成功提取出来,并且各个模态分量间频域重叠分量最小；相比于BEMD的分解结果图5(b),IMF1和IMF2中有周期分量,但是在之后的模态中,嘈杂信号占主导,结合频域图5(d)分析,IMF1的频域带宽甚大,换而言之,IMF1与各个模态间存在模态混叠现象,而在频域中存在端点效应,在图中见红色圆圈标记处。综上所述,无论是时域周期性分量对比,还是频域故障特征的有效提取,所提算法均表现出一定的优越性和准确性,因此该算法具有一定的实用意义。

5 实际数据

为了更近一步验证该算法的实用性,现采用实际情况下采集的真实数据进行处理,并设置对比实验,对结果进行定性定量的分析和比较。

数据来源于Paderborn University轴承数据集[17],实验测试台如图6所示,测试中的轴承为6203型球轴承,轴承的滚子数和滚子直径分别为8 pc、6.75 mm,轴承节径为28.55 mm,接触角为0°,振动传感器的采样频率为64 kHz,该实验采用的数据是在转速为1 500 r/min的情况下,由电机超负荷运转所造成的真实损坏样本集,其中包括内圈故障信号、外圈故障信号和内外圈复合故障信号。

图6 实验测试台Fig.6 Experimental test platform

原始数据的时频域见图7,由图可知,时域中信号分布杂乱,频域中各个频段都幅值都很突出,无法通过简单的信号变化来提取故障特征,对原始信号分别采用文中故障诊断算法、级联VMD和MEMD算法进行分解,对比分析结果得出最终结论。

图7 原始数据时频域Fig.7 Raw data time frequency domain

首先,用AMVMD算法对原始信号进行分解,在分解过程中,优化算法的参数设置见表1,狼群的寻优空间如图8(a)所示,在该空间内以最小模态重叠分量为目标函数,当该函数取到最小值时,返回模态数k和惩罚参数α所对应的值,由图8(b)可知,当算法进行第85次迭代时,目标函数值最小为 0.877 1,模态分量k=7,惩罚参数α=3 290。

图8 参数寻优过程图Fig.8 Parameter optimization process diagram

此时MVMD将按照返回的参数值对原始信号进行分解,所得模态分量的时频域见图9(a)和图9(b)；随后,使用级联VMD算法对原始信号进行分解,为保证两种算法的可对比性,模态分量k和惩罚参数α均与AMVMD模型保持一致,3种信号同时由3个并联的VMD模型进行分解,最后将同一本征模态上的信号显示在相同坐标轴上,模态分量的时频域结果见图9(c)和图9(d)；最后,由MEMD算法对3种信号进行自适应分解,由信号分解结果图9(e)和图9(f)可知,原始信号被分解为11个模态分量,MEMD在EMD基础上将一维输入信号拓展到多维,但是也继承了原始算法的局限性。

图9 3种算法对比图Fig.9 Comparison of the three algorithms

对比分析3种算法分解的结果图,其中蓝色表示内圈信号,橙色为复合信号,绿色为外圈信号,由MEMD分解的时域图9(e)可以看出,信号分解顺序是由高频到低频,结合频域图,在图9(f)中IMF1的频带带宽甚大,如左侧放大图中,模态分量间存在严重混叠现象,这意味着故障特征大概率的被分解到多个模态中,一方面,削减了故障特征的信号能量,另一方面,也大大提高了特征提取的难度；相反,对比级联VMD分解的结果,时域信号相比MEMD分解结果周期信号的收敛性大大提升,不足的是同一模态分量的中心频率不一致,如图9(d)左侧放大图所示,IMF4中内圈信号的频带中心与其他信号的频带中心有很大间距,同样的问题也存在与IMF5中,这也是级联VMD需要改进的地方；相比之下,如图9(a)所示AMVMD即能在时域中最大限度的提取周期性分量,在频域中也有模态对齐的特性,就是将相同中心频率的有限带宽分解到同一个模态,为后期实际工程应用提供了很大的便利,有一定的实际意义。

图10 3种算法包络图Fig.10 Envelope graphs of the three algorithms

为了定量分析实验结果,现对以上3种算法分解的模态分量做故障特征系数分析,计算见式(14)。选取每种算法中最佳的模态进行包络对比,引入特征幅值和信噪比(SNR)作判断指标,做定量分析。

图10中(a)、(b)、(c)依次表示AMVMD包络结果、级联VMD包络结果、MEMD包络结果,3种算法的详细评价指标见表2。对比分析,MEMD的特征提取能力最差,只有复合特征被提取出,并且特征幅值最小；级联VMD提取出外圈故障特征和复合特征的倍频信号,相比于MEMD中噪声信号增大,但是故障特征明显且幅值有一定的提升；所提的AMVMD算法提取的特征全面,且幅值最大,避免了MEMD算法所存在的模态混叠,特征能量削弱的问题,同时,相比较级联VMD又有模态对齐特性,无论在学术研究领域还是工程应用上均有一定的优越性和实际意义,为下一步的特征识别奠定基础。

(14)

表2 3种方法的性能评价Tab.2 three algorithms performance evaluation

6 结 论

本文提出一种自适应多元变分模态分解算法,将多元变分模态与混合灰狼优化算法相结合,以最小模态重叠分量作为目标函数,进行本征模态数k和惩罚参数α寻优,当目标函数取到最小值时,返回最优参数,MVMD将按照最优参数对原始信号进行自适应的分解,将实验结果与BMED、级联VMD和MEMD进行比较,设置仿真信号和实际数据进行验证分析,由最终结果得出该方法的高效性和实用性。

该算法一方面解决了人为参数经验设置的弊端,另一方面,所分解的信号具有模态对齐特性,大大提升了该算法的实用性和工程意义。