测井用电动挤压式橡胶集流器集流性能分析
2022-12-01孔维航赵功达刘嘉宇邢光龙
张 曦, 孔维航,2,3, 赵功达, 刘嘉宇, 李 雷, 邢光龙
(1. 燕山大学 信息科学与工程学院,河北 秦皇岛 066004; 2. 河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛 066004;3. 河北省软件工程重点实验室, 河北 秦皇岛 066004; 4. 山东工商学院 信息与电子工程学院, 山东 烟台 264026)
1 引 言
测井用集流器作为集流型测试仪器的重要组成部分,其高集流度是保证低产低流速油井产液剖面测量参数准确检测的前提和基础。近年来,用于国内油井产液剖面测试的集流装置主要有伞式集流器[1]、皮球式集流器[2]等。在伞式集流器研究方面,朱洪征等[3]提出一种基于油管输送+存储式采集模式的集流测井方法,其使用的伞式集流器依靠摩擦块与套管内壁的摩擦力将伞机构撑开,提高了低产低流速情况下的集流度;马宝全等[4]在传统集流伞结构基础上设计一种溢气型集流装置方案,有效排除气体对集流测量的影响。在皮球式集流器研究方面,许福东等[5]使用双皮球替代传统的单皮球结构,并通过实验验证了方案的可行性;刘合等[6]在双皮球的基础上,通过检测皮球压力进行井下集流状态的动态监测,显著提高了测调效率。然而,目前常规伞式集流器工作时因伞筋与套管之间存在的缝隙使得漏失较为严重,皮球式集流器下井皮球易刮破、注液控制不当易爆破,这将会严重影响测井仪器的测试精度。因此,保证测试仪器在井下的正常稳定工作,仍是当前集流测量模式产液剖面动态监测的关键。
基于油管输送测井工艺[7],本文提出一种高可靠电动挤压式橡胶集流器结构模型,其特点为使用一段管柱橡胶弹性件作为集流器的核心部件。根据有限变形理论,利用变形梯度和超弹性本构模型分析橡胶弹性件的形变特性,通过COMSOL有限元仿真软件对橡胶弹性件进行受力挤压仿真实验,分析不同结构、材料属性等参数对橡胶弹性件集流性能的影响,根据仿真优化数据研制橡胶集流测试仪器,并在模拟井实验平台上验证其集流性能。
2 电动挤压式橡胶集流器结构模型
2.1 橡胶集流器的工作原理
基于油管输送测井工艺的电动挤压式橡胶集流模型见图1所示,其中橡胶弹性件为超弹性材料,受到挤压时形状改变而总体积近似不变,且卸去外力后可恢复至初始状态,图1中弹性件为受力压缩状态。电动挤压式橡胶集流器的工作原理是:驱动电机供电后带动滚珠丝杠进行轴向伸缩式直线运移,通过销钉、滑套等结构对橡胶弹性件施加推力进行轴向压缩,受挤压的弹性件发生弹性形变,产生径向的肩凸,随着轴向压缩量程的增大,肩凸与套管内壁接触以达到密封油套管环形空间的效果,使得管内流体只能经进液口进入集流器内部而实现集流。集流器的收回动作则为上述过程的逆过程,即驱动电机反转,带动丝杠等反向运动将橡胶弹性件拉回至初始态。
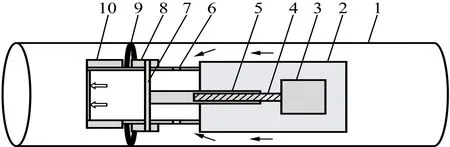
图1 电动挤压式橡胶集流模型Fig.1 Structure of electric extruded rubber flow collector for logging1-套管; 2-轴向电机驱动短接; 3-轴向驱动电机; 4-滚珠丝杠; 5-丝扣推杆; 6-进液口; 7-销钉; 8-滑套; 9-橡胶弹性件; 10-管柱橡胶集流短接
2.2 橡胶弹性件的结构设计
橡胶弹性件作为整个集流器的核心构件,其在受挤压过程中可产生径向向外的肩凸和接触套管时可产生一定的接触应力为结构的关键。基于油管输送测井工艺实际特点和弹性件受力形变规律,设计3种橡胶弹性件结构(如图2所示)分别为标准管柱型、梯形内凹型、圆弧内凹型,并通过有限元仿真研究对比分析不同结构橡胶弹性件的集流性能。图2所示3种方案的主体结构主要包括连接滑道的弹性件驱动机构安装槽、用于封隔或打开油套管环形空间的弹性件主体和用于套接集流通道外侧的弹性件安装槽。
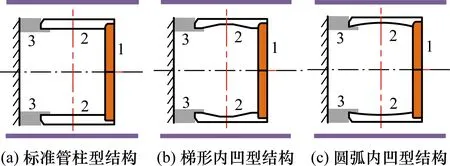
图2 橡胶弹性件3种设计结构图Fig.2 Three design structures of rubber elastomer1-弹性件驱动机构安装槽; 2-弹性件主体; 3-弹性件安装槽
为开展橡胶弹性件受力挤压有限变形机理和集流性能研究,拟以橡胶弹性件为研究对象,结合橡胶弹性件主体几何、材料双重非线性特点以及形变后弹性件主体与套管内壁接触非线性特点,建立橡胶弹性件仿真模型,利用接触和接触摩擦作用机制揭示弹性件主体受力变形和密封程度在不同情况下的变化规律。
3 橡胶弹性件有限变形机理
3.1 橡胶弹性件受力变形机理
橡胶弹性件的核心作用是实现对油套管环形空间的封隔,其形状为空心圆柱套筒,工作方式为通过轴向压缩形变产生向外的肩凸,并逐渐与油套管接触产生接触应力实现全集流。图3为标准管柱型橡胶弹性件受力形变模型,为了进一步分析橡胶弹性件在受到轴向力Fz时的形变特性,在有限变形理论中拟以变形梯度进行详细分析。
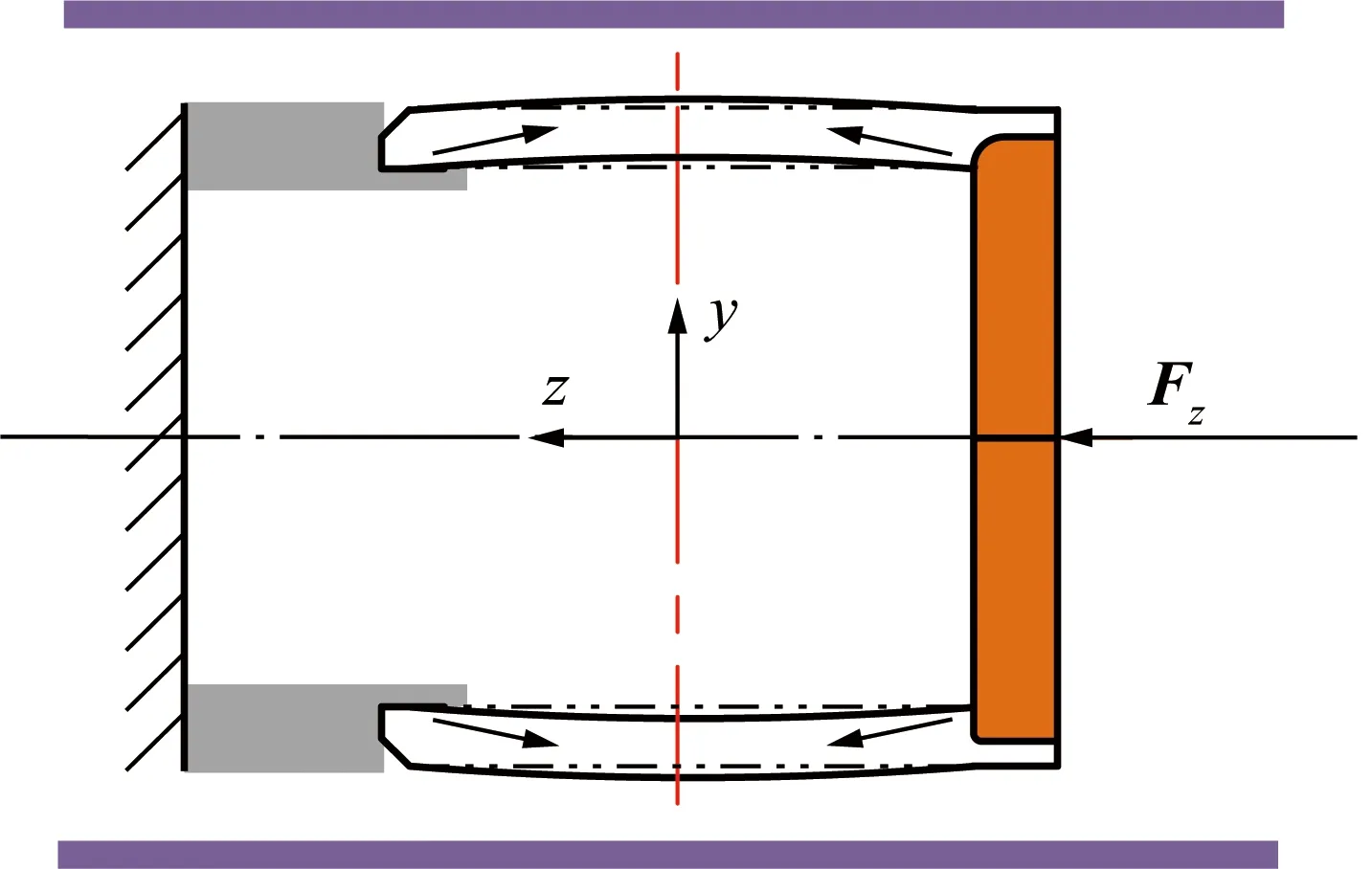
图3 橡胶弹性件受力形变模型Fig.2 Model for force deformation of elastomers
设P和Q分别表示变形前后典型物质点的位置矢量,Yi为随体坐标(Lagrange坐标),其位移u为[8]:
u=Q-P
(1)
弹性件变形前后的基矢分别为:
(2)
利用Kronecker符号可得到逆变基矢分别为:
(3)
变形梯度张量F和逆张量F-1分别为:
F=Qi⊗Pi,F-1=Pi⊗Qi
(4)
式中⊗表示并矢。
将变形梯度张量F分解:
F=R·U=V·R
(5)
式中:R为正常正交张量,表示转动;U、V为对称正定张量,分别为Lagrange型、Euler型应变张量;“·”表示点积。
在现时构形上,Euler应力张量满足:
σ=σT, ∇·σ+f=0,σn=σ·n
(6)
式中:n为面力作用的外法线;σn为Euler应力矢量;f为初始构形和现时构形中的梯度算子。
同时,为方便功共轭讨论拟引入Kiechhoff应力张量,它可由Euler应力和Piola-kirchhoff应力S获得[9]:
(7)
式中:J=det(F)为体积比;W为橡胶材料的应变能密度;E为单位矩阵;Piola-kirchhoff应力S为Lagrange应力张量,它的引入是因Euler应力为定义在现时构形上每单位面积的接触力,是与变形相关的真实应力。
3.2 Mooney-Rivlin超弹性本构模型
橡胶材料是一种典型的超弹性材料,其弹性性能与硬度、载荷大小、载荷频率等多种因素有关,不能以简单的弹性模量来表征[10]。目前常采用数学方法建立本构模型如Neo-Hookean模型、Yeoh模型、Ogden模型、Mooney-Rivlin模型等用于描述橡胶材料的受力形变规律,其中Mooney-Rivlin模型应用较广泛[11]。
Mooney-Rivlin模型描述橡胶弹性时,认为橡胶的形变为各向同性的均匀形变,且橡胶作为一种超弹性材料,具有体积近似不可压缩的特性,其本构关系为[12]:
(8)
式中:σij为Euler应力张量的分量;p为静水压力;Bij为左Cauchy-Green变形张量的分量;I1、I2、I3分别为变形张量的第1、第2、第3不变量。
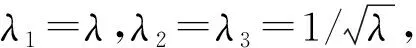
(9)
由F可得出变形张量的3个不变量分别为:
I1=tr(B)=λ2+2λ-1
(10)
(11)
I3=1
(12)
在橡胶材料的工程计算中Mooney-Rivlin应变能函数的应用较为广泛[12],其表达式为:
(13)
式中Cij为模型的待定参数。
关于橡胶材料的单轴加载计算通常取Mooney的两项式:
W(I1,I2)=C10(I1-3)+C01(I2-3)
(14)
通过修改模型参数C10、C01可表征不同属性的橡胶弹性件。
4 仿真研究
4.1 橡胶集流器仿真模型构建
为了提高集流器封隔过程的有限元分析效率,依据油管输送测井工艺下集流器的工作流程,可将集流结构部件进行简化,其简化后的结构模型如图4(a)所示。图4(a)所示橡胶弹性件、橡胶安装槽、滑套和套管同轴状态下,集流器呈轴对称几何结构,其所受坐封载荷和约束也是呈轴对称分布,因此采用二维轴对称结构构建仿真模型并对橡胶与套管的接触应力进行分析。
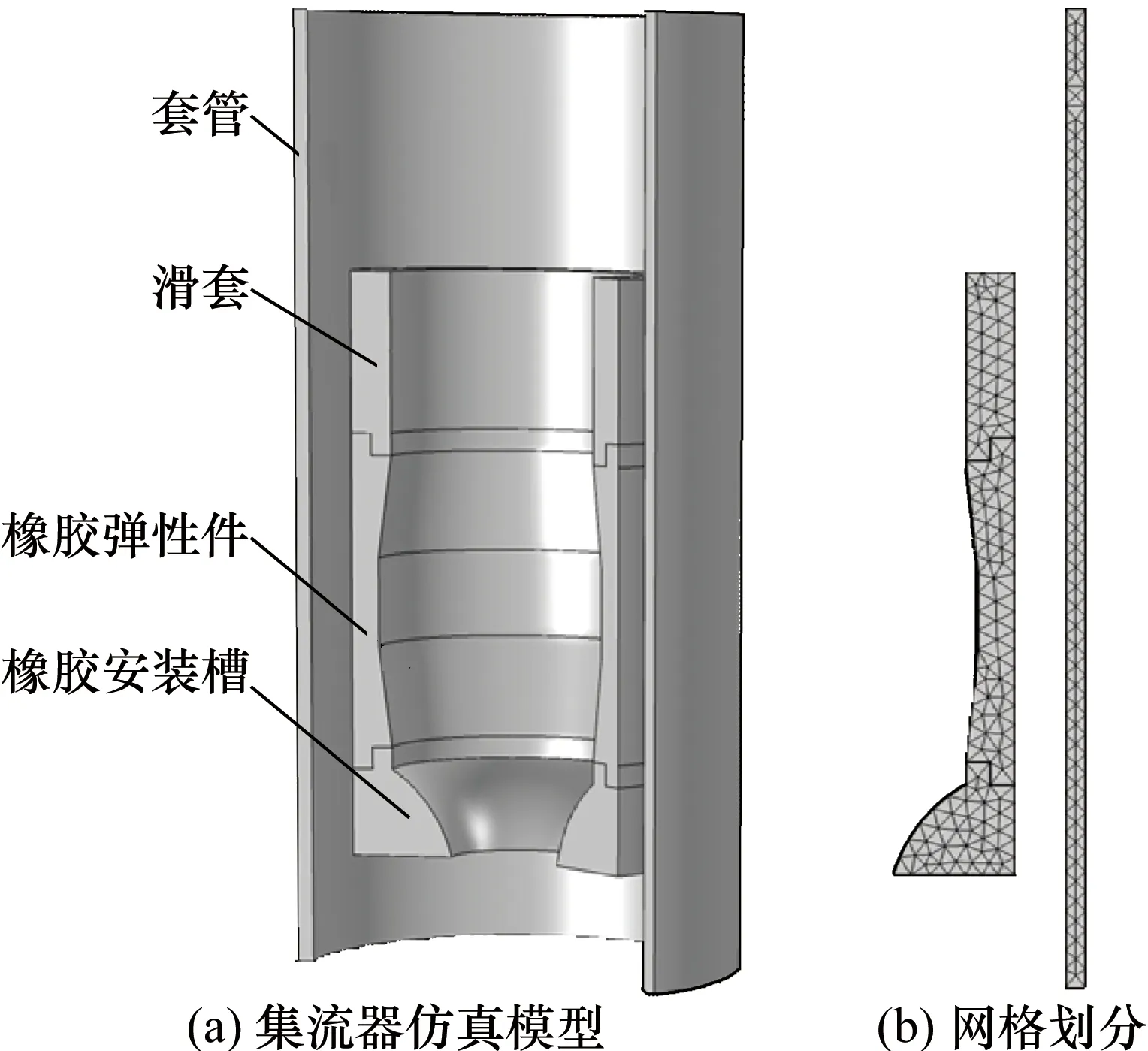
图4 集流器仿真模型及网格划分Fig.4 Collector simulation model and mesh of the collector
橡胶弹性件结构以梯形内凹型为例,取套管内径为125 mm、橡胶弹性件内径为76 mm、厚度为12 mm、长度为80 mm、管柱橡胶集流短节最细处内径为36 mm,利用COMSOL有限元仿真软件构建二维轴对称结构仿真模型如图4(b)所示,其网格划分采用自由三角形单元,最大单元大小为4.2 mm,增长率为1.2。图4(b)中定义对橡胶安装槽施加固定约束,通过设置滑套位移的方式实现对橡胶弹性件的单轴压缩,对套管的两端同样施加固定约束[14]以保证接触的稳定性。
集流器橡胶弹性件的受力形变及二维截面应力分布分别如图5所示。图5中橡胶弹性件受滑套挤压,产生径向向外的肩凸,由图5可知套管受肩凸挤压产生了一定的应力,此时的单轴挤压量程为21.2 mm。
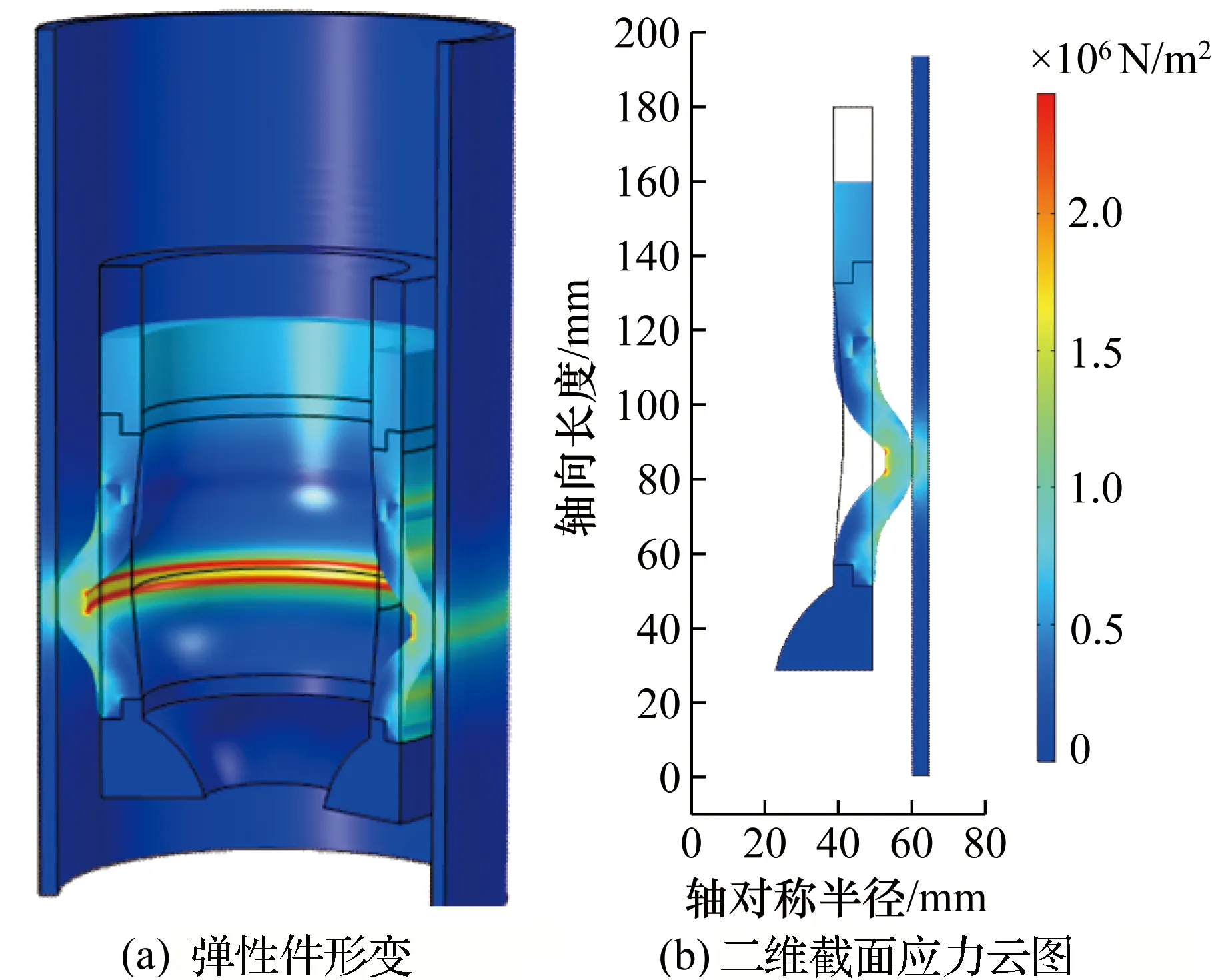
图5 弹性件发生形变及二维截面应力云图Fig.5 Deformation of the rubber elastomer and two dimensional section stress nephogram
4.2 集流器集流性能评价方法
分析集流器橡胶弹性件密封性能优劣,不仅需要考弹性件与套管之间接触应力的大小,而且需要考虑接触应力的分布情况。故采用接触应力分布对轴长的积分值K[15]来评价集流器的集流性能,K越大,集流性能越好。K的表达式为:
(15)
式中:VL为套管的应力分布;L为套管长度。
根据图5套管与橡胶接触面的应力分布情况,绘制轴向应力分布曲线,如图6所示,由式(15)得出此时的K值为41 751 N·m-1。
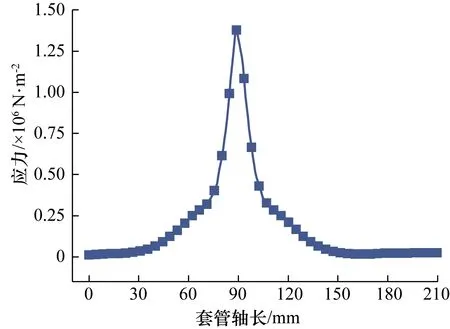
图6 套管的轴向应力分布Fig.6 Axial stress distribution of the pipe
对集流器橡胶弹性件集流性能变化规律的研究将以图4模型参数为初始值,以套管的轴向应力分布积分值K为判断依据,对比分析不同参数下标准管柱型、梯形内凹型、圆弧内凹型3种结构弹性件的集流性能。
4.3 橡胶硬度对集流性能的影响
橡胶弹性件的硬度对集流器的集流性能有较大的影响。高可靠集流器的机构设计要求所使用的橡胶弹性件受力后产生肩凸,且产生的肩凸需满足一定的硬度才可提供足够的接触应力而达到集流的效果。不同硬度下,挤压橡胶的材料力学参数[10,16,17]见表1。实验方法为使用不同参数的Mooney-Rivlin模型来模拟不同硬度的橡胶弹性件,以套管与不同结构弹性件接触时的应力积分值K来对比分析不同方案的集流性能。
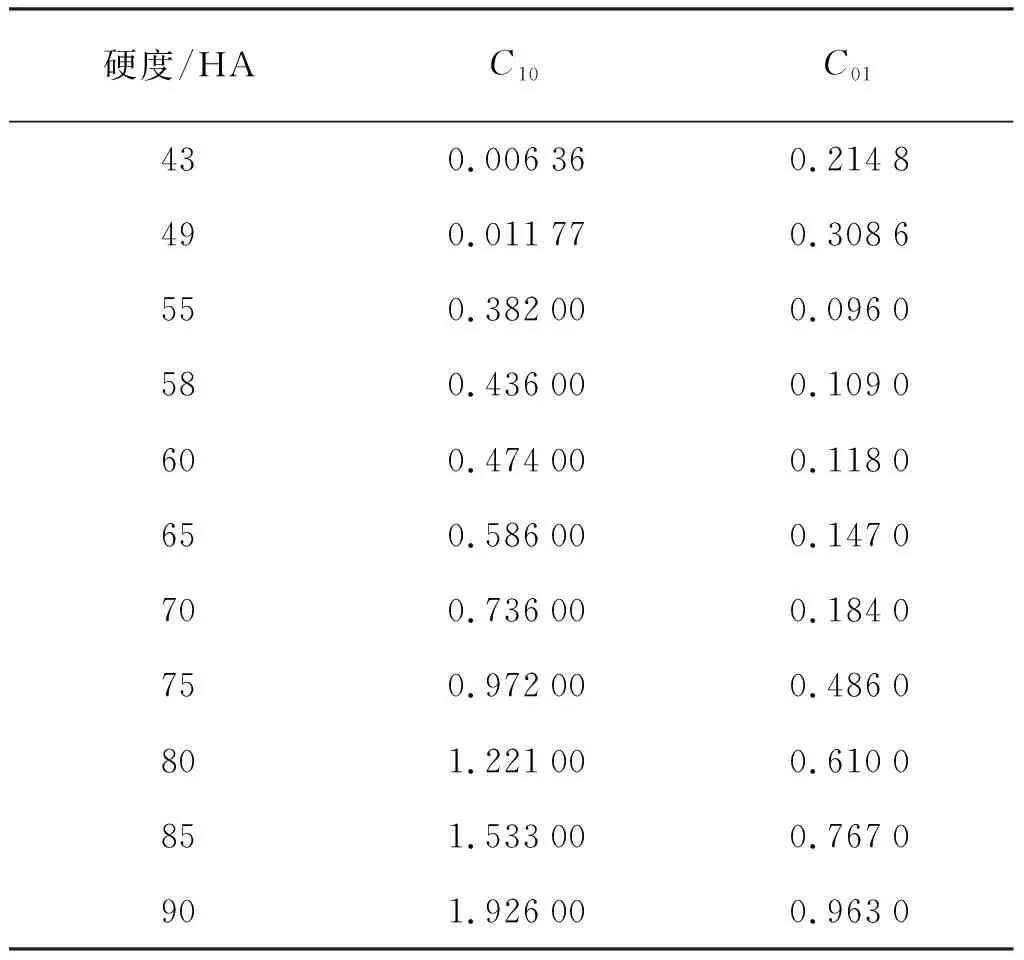
表1 不同硬度橡胶的Mooney-Rivlin参数Tab.1 Mooney-Rivlin parameters for different hardnesses of rubber MPa
图7为套管应力分布积分值K随弹性件硬度的变化情况。由图7可知,不同结构集流器的集流性能对弹性件硬度变化的响应趋势近似相同,随着硬度的提高,各结构集流器的集流性能均有提高,且在硬度大于65HA后提升效果更加显著;相同橡胶硬度下,不同结构弹性件的集流性能排序为圆弧内凹型>梯形内凹型>标准管柱型,其中梯形内凹型与圆弧内凹型集流性能相近,标准管柱型最差且与前两者有较大差距。故轴向挤压量程一定时,在电机驱动能力的范围内,选择硬度较大的圆弧内凹型橡胶弹性件有助于提高电动挤压式橡胶集流器的性能。

图7 硬度对集流性能的影响Fig.7 Effect of hardness on flow collector
4.4 摩擦系数对集流性能的影响
摩擦系数作为表征材料摩擦学性能的重要指标,其对集流系统中橡胶弹性件与套管的接触状态有较大影响[18]。在实验结果的基础上,以摩擦系数为参量[19],实验分析其对集流性能的影响。实验时弹性件硬度取58HA,设置摩擦系数的范围为0.1~0.8,以步长为0.1取8组数据进行压缩仿真研究,对比不同结构橡胶集流器的集流性能。
图8为套管应力分布积分值K随弹性件硬度的变化情况。由图8分析可知,弹性件与套管间的摩擦系数对集流器的集流性能有一定影响,随着摩擦系数的增大,3种结构的应力分布积分都有增大的趋势,即集流性能有所提高;相同摩擦系数下,不同结构弹性件的集流性能排序为圆弧内凹型>梯形内凹型>标准管柱型。
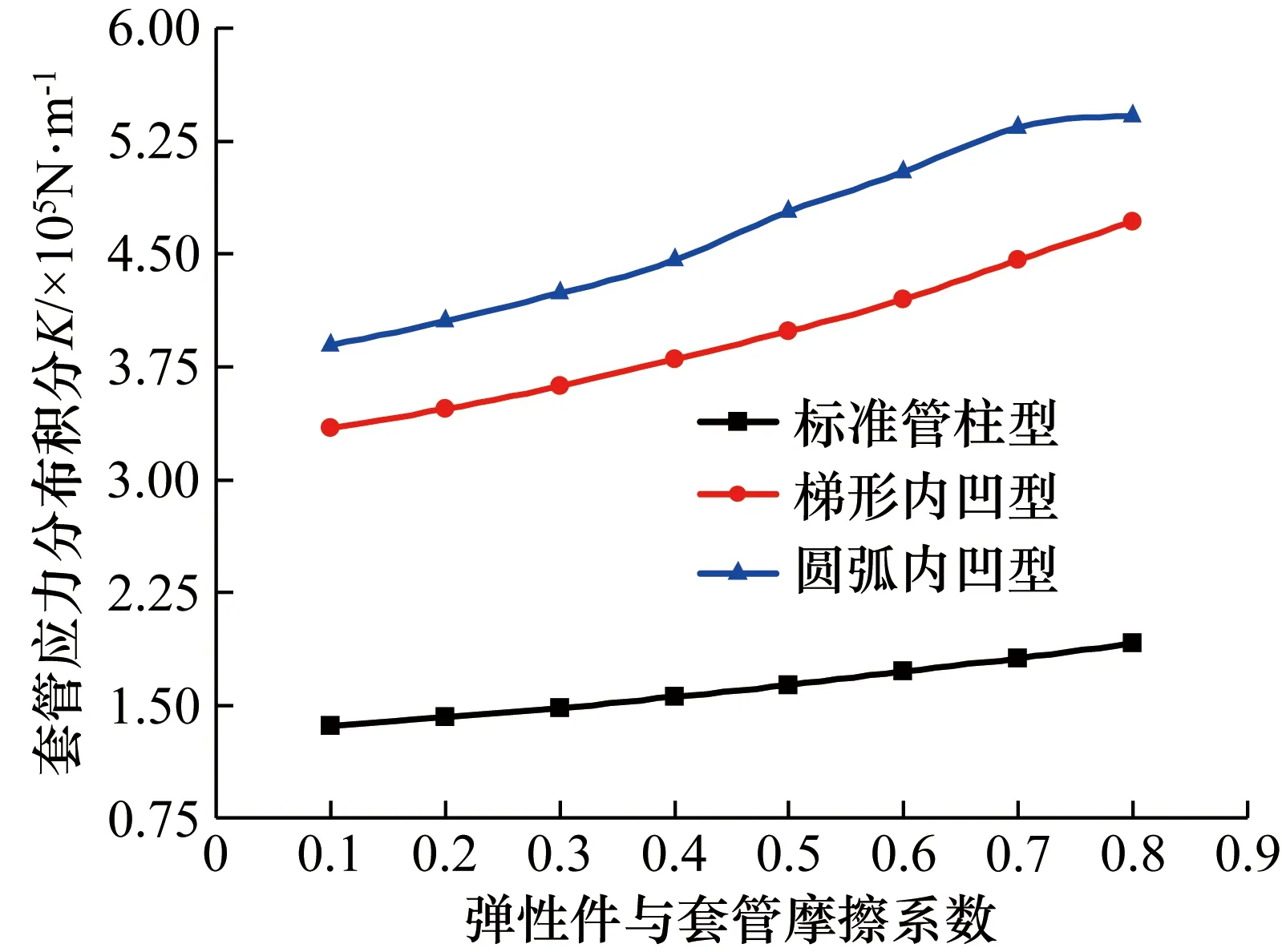
图8 摩擦系数对集流性能的影响Fig.8 Effect of friction coefficient on flow collector performance
4.5 橡胶内凹程度对集流性能的影响
根据实验结果,相同条件下圆弧内凹型弹性件的集流性能优于梯形内凹型结构,标准管柱型结构与前两者有较大差距,可见内凹型的结构更易于达到集流的效果。该部分的实验即以此为基础,探究内凹程度对2种内凹型弹性件集流性能的影响。实验方法为以内凹量为变化量进行轴向挤压仿真研究,设置橡胶硬度为58HA,不考虑接触摩擦的影响,分析2种内凹结构套管应力分布积分值K对内凹量的响应规律。其中内凹量指的是内凹结构的最薄处与橡胶厚度之差。
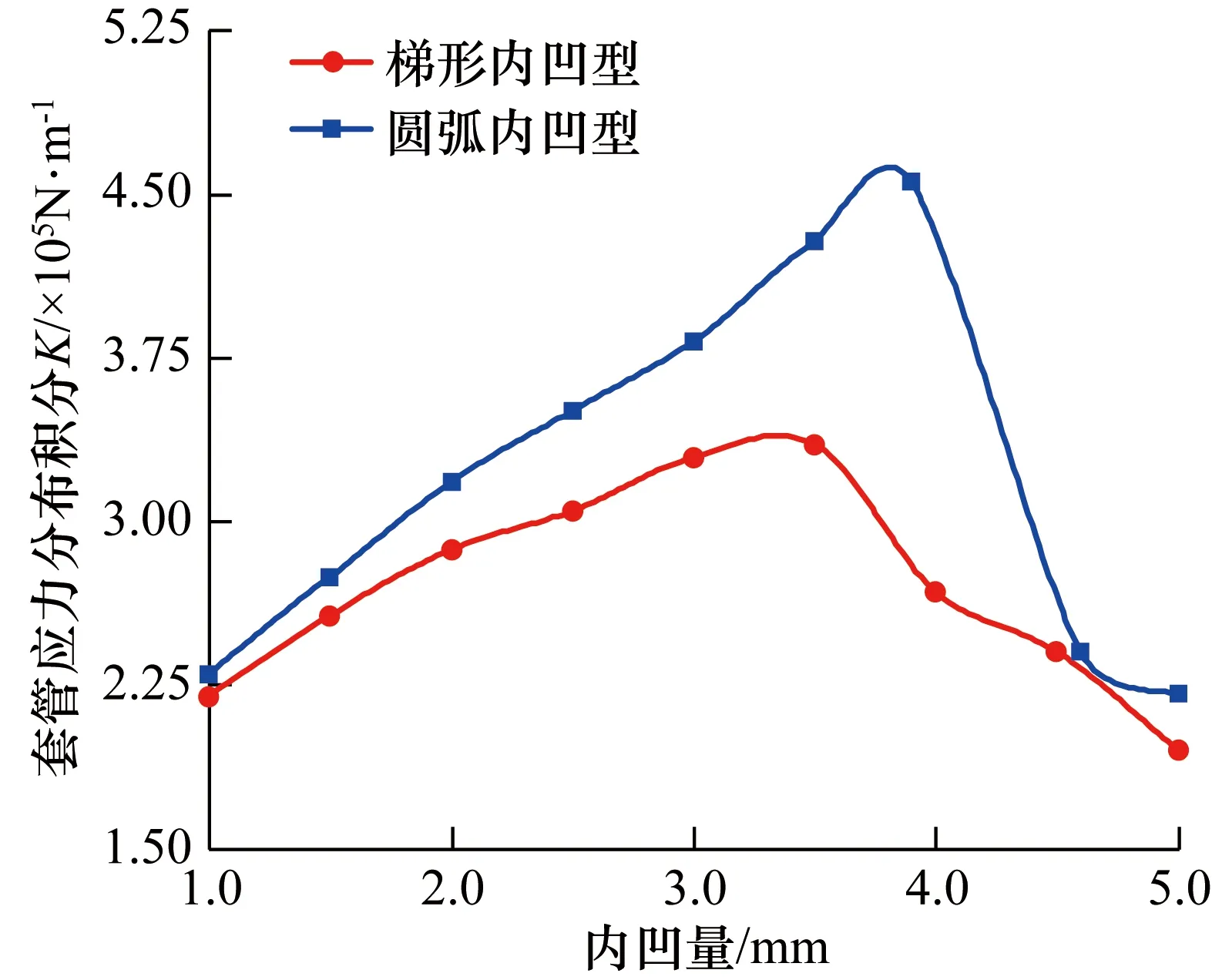
图9 内凹程度对摩擦系数的影响Fig.9 Effect of concave degreen on the flow collection performance
图9为套管应力分布积分值K随内凹量的变化规律。由图9分析可知,相同条件下,使用圆弧内凹型弹性件的集流器集流性能优于使用梯形内凹型弹性件的集流器;圆弧内凹型和梯形内凹型弹性件的集流性能随内凹量的变化规律均为先增高,在内凹量为3~4 mm时达到最大值,而后出现下降趋势。结果表明增加弹性件的内凹程度有助于提高其集流性能,但内凹量过高亦会导致橡胶与套管的接触部分过于薄弱而使接触应力降低,从而造成集流性能下降。
5 实验结果分析
5.1 弹性件及集流装置研制
依据结构分析和仿真结果,研制了一种可提高可靠集流器性能的橡胶弹性件。研制的橡胶弹性件主要满足以下技术要求:橡胶弹性件整体为空心圆筒形,圆筒的一端设有安装槽,另外一端为加厚设计,以保证弹性受力挤压时的稳定性;圆筒的内侧为仿真研究中性能最优的圆弧内凹形结构,圆弧的顶点在圆筒轴长的1/2位置,以确保其受力挤压时可产生径向向外的肩凸;弹性件的具体尺寸与仿真尺寸一致。弹性件内径为76 mm、厚度为12 mm、长度为80 mm;内凹程度和硬度取仿真研究的较优结果,结合电机的驱动能力并考虑橡胶的弹性,硬度设计为58 HA,内凹程度取4 mm。此外,为保证井下工作的耐久性,弹性件的材质选取具有耐高温、耐高压、耐腐蚀等特点的丁腈橡胶[19]。橡胶的结构如图10所示。

图10 橡胶弹性件实物Fig.10 Rubber elastomer devices
在橡胶弹性件的基础上,根据图1的电动挤压式橡胶集流器模型,搭建驱动挤压行程的外围结构,其结构实物如图11所示,其机身有进液口用于集流态液体流入,两端有扶正器保持机身姿态,内部还有涡轮流量计用于测量流入的液体流量。

图11 橡胶集流器整体结构Fig.11 Overall structure of the rubber flow collector
5.2 实验方法
为检验橡胶集流器在连续油管输送工艺下的集流性能,测试实验以实际工程应用为导向,在大庆油田水平井多相流模拟实验平台(图12)上进行标定,实验所用流体介质为柴油和水的混合液,水占液体总流量比重为85%,通过计量管段标准计量后进入模拟井筒,井筒内放置集流装置。实验时使用图12(a)所示常规伞式集流装置作为对照,对比分析橡胶集流装置与常规伞式集流装置的性能差异。

图12 水平井筒多相流模拟装置平台Fig.12 Rubber flow collector and umbrella flow collector in simulated wellbores
5.3 实验分析
5.3.1 数据采集
在实验平台上,集流装置对模拟井筒进行封隔,混合液经进液口进入仪器驱动内部的涡轮流量计,同流量工况下,涡轮响应越快,说明流经仪器的流量越多,则集流性能越好。实验过程中,测试的标准总流量数据为1 m3/d、2 m3/d、3 m3/d、5 m3/d、10 m3/d、20 m3/d、30 m3/d、40 m3/d、50 m3/d、60 m3/d,通过采集不同流量工况下涡轮流量计的响应数据分析集流装置的集流性能。流量为20 m3/d时橡胶集流器的涡轮响应如图13所示。
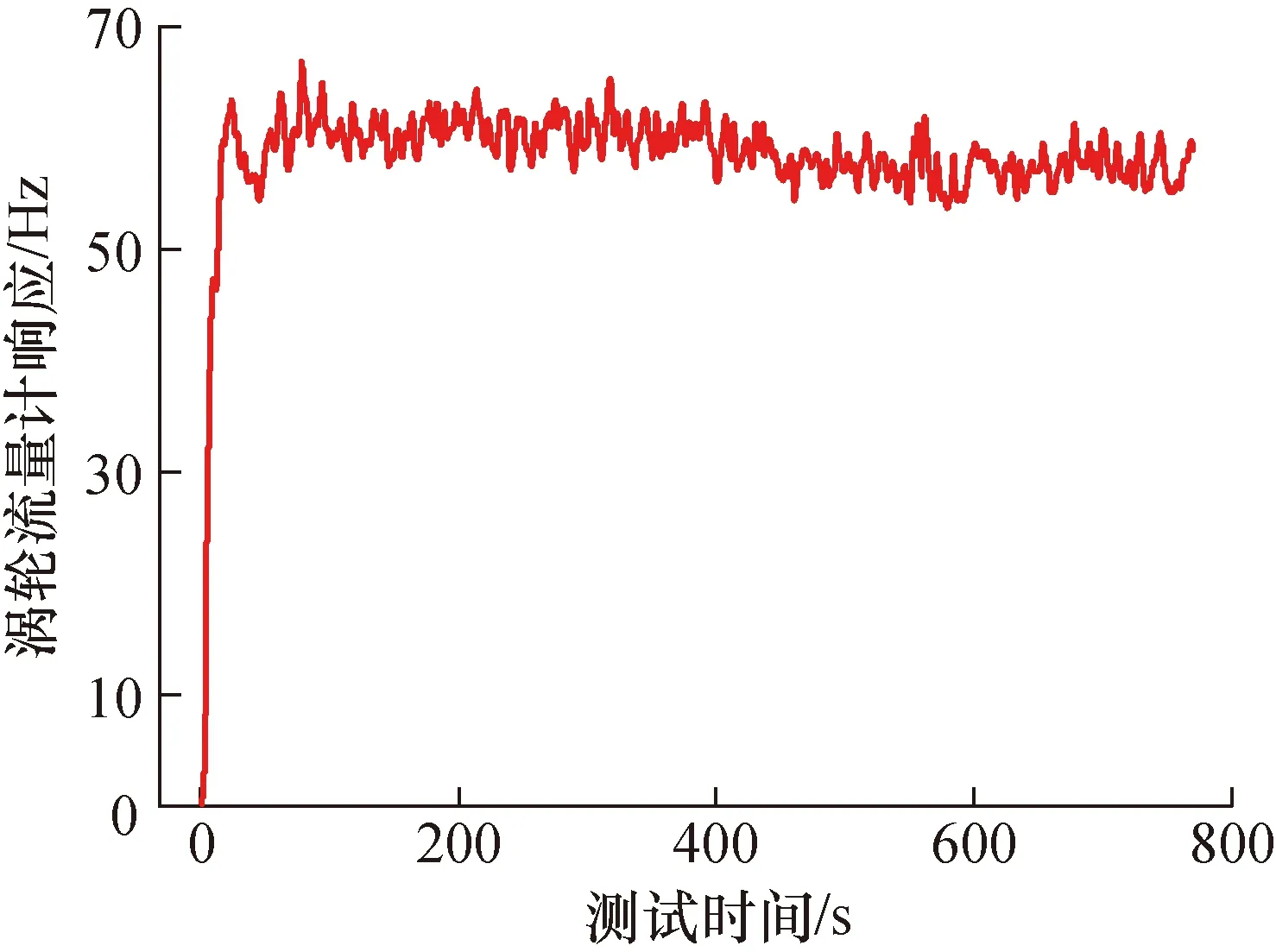
图13 流量为20 m3/d时橡胶集流器的涡轮响应Fig.13 Turbine response of a rubber collector at a flow rate of 20 m3/d
5.3.2 实验结果分析
当响应频率趋于稳定时,对采集的数据取平均值,作为当前工况的涡轮响应数据。在不同流量工况下,分别对橡胶集流器和常规伞式集流器进行动态实验,实验结果如图14所示。
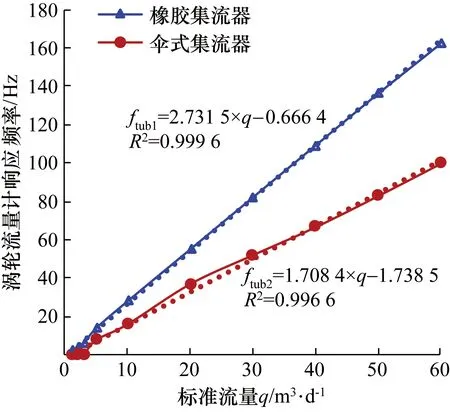
图14 不同流量工况下的涡轮响应Fig.14 Turbine response at different flow conditions
由图14分析可知,相较于伞式集流器,相同工况下橡胶集流器的涡轮响应更快,集流度更高;同时,橡胶集流器结果的线性拟合曲线斜率更大,拟合优度R2达到0.999 6,线性度更好。综上结果表明,所提电动挤压式橡胶集流器的集流性能更优,在石油生产测井方面能够发挥重要作用。
6 结 论
本文通过理论分析有限变形机理,提出了一种电动挤压式橡胶集流器结构,解决传统常规集流器存在漏失严重、易刮破爆破等问题;提出了3种弹性件结构,通过仿真实验,以套管轴向应力积分值K为指标分析不同情况下各结构的集流性能;研制了电动挤压式橡胶集流整体装置,并进行动态实验验证。
1) 在相同硬度、尺寸、摩擦系数情况下,得出不同结构橡胶弹性件的集流器集流性能,圆弧内凹型结构>梯形内凹型结构>标准管柱型结构。
2) 相同条件下,提高橡胶硬度可增强集流器的集流性能,实际工程应用中应在考虑电机负载能力同时使用较硬的橡胶以满足集流性能要求;增大橡胶与套管壁面的摩擦系数可提高集流器的集流性能;弹性件的内凹程度与集流性能呈非线性关系,增大内凹程度有助于提高集流性能,但弹性件变薄亦会导致接触应力减小降低集流性能。
3) 实验结果表明,在相同流量工况下,橡胶集流器的集流性能优于传统伞式集流器,这也验证了仿真分析的正确性。
