镜像铣加工过程中薄壁工件变形和振动的预测

王建山，何天宇，肖聚亮，刘海涛

镜像铣加工过程中薄壁工件变形和振动的预测

王建山，何天宇，肖聚亮，刘海涛

(天津大学机械工程学院，天津 300072)

镜像铣是大型薄壁工件加工的有效方法，在航空航天等重要领域有着广泛的应用．镜像铣加工过程中薄壁工件的变形和振动是影响加工精度的主要因素，如何准确预测镜像铣加工过程中薄壁工件的变形和振动是优化加工参数、提高加工精度的关键问题．本文基于金属切削原理并考虑了薄壁工件加工过程中的弯曲变形和铣削力相互作用，建立了铣削力预估模型．在此基础上，结合薄板小变形理论和有限元法，建立了考虑加工过程中材料去除和铣削力与支撑同步运动的薄壁工件镜像铣动态力学模型．通过仿真模拟，研究了支撑刚度、支撑阻尼、主轴转速和进给率对薄壁工件变形和振动的影响规律．结果表明，在镜像铣加工过程中薄壁工件的变形随着支承刚度的增加而减小，振动幅值随着支撑阻尼的增加而减小．最后，对6061铝合金薄板的镜像铣加工实验与本文建立模型的时域和频域信号进行了比较．振动数据采集点处的模型预测结果与实验相差小于5%，二者对比结果表明所建立的模型能够对薄壁工件加工过程中的变形和振动进行准确的预测．镜像铣加工相比于直接铣削加工，薄板加工点处的振动幅值从71.61μm减小到5.71μm，对比结果表明柔性支撑结构能够有效地减小加工过程中薄壁工件的振动．本文工作有助于提高薄壁工件的镜像铣加工精度．

镜像铣；薄壁工件；变形；振动；预测；支撑；加工参数

薄壁工件作为飞机蒙皮、火箭贮箱等柔性结构的关键部件被广泛应用于航空航天领域[1]．薄壁工件由于尺寸大、厚度薄和刚度低等特点，在加工过程中极易发生变形和振动．镜像铣削是目前大型薄壁工件加工的有效方法[2]．镜像铣削系统由铣刀、支撑和机器人组成，一侧机器人安装铣刀，作为加工机器人对薄壁工件进行铣削加工；另一侧机器人安装支撑，作为支撑机器人对薄壁工件进行支撑，在加工过程中铣刀和支撑保持镜像同步移动．镜像铣削系统提高了薄壁工件支撑位置附近的局部刚度和阻尼，能够有效抑制加工过程中薄壁工件的变形和振动，而镜像铣削加工精度在很大程度上受限于加工过程中薄壁工件的变形和振动．因此，如何准确预测复杂镜像铣削加工条件下薄壁工件的变形和振动，以及优化加工参数是提高加工精度必须解决的难题[3]．

薄壁工件在铣削加工过程中的变形和振动行为一直受到众多关注．Zhang等[4]通过有限元研究了薄壁工件铣削加工过程中随着材料去除、薄壁工件变形挠度和动态特性的变化．Bao等[5]使用有限元仿真软件，分析了支撑点数量和支撑点与铣刀相对位置对薄壁工件加工过程中变形的影响，优化了支撑的运动路径，并用实验进行了验证．Li等[6]通过铣削实验研究了随动支撑机构中液体压力对薄壁工件变形的影响规律．Zhang等[7]对薄壁工件加工过程中不同位置的变形进行了有限元仿真，提出了一种预测加工表面误差的方法．Jiang等[8]探究了薄壁工件加工过程中残余应力对变形的影响，提出了减小薄壁工件变形的铣削加工顺序．

除了镜像铣削加工过程中的变形，薄壁工件振动行为的研究也取得了较大进展．Shi等[9]建立了考虑铣刀移动的薄壁工件振动模型，研究了表面阻尼材料属性和材料粘贴位置对薄壁工件侧铣加工过程中振动的影响．Arnaud等[10]基于有限元软件，考虑了加工过程中材料的去除，研究了三角形薄壁工件铣削加工过程中不同位置处的振动行为．Lan等[11]基于理论模型分析了柔性支撑结构支撑刚度、阻尼系数对薄壁工件不同位置模态参数的影响．Wang等[12]为了抑制薄壁工件车削加工过程中的振动，开发了镜像车削系统，建立了镜像车削中薄壁工件振动模型，对工件加工中动态响应进行预测分析．Bo等[13]通过锤击实验研究了镜像铣削支撑结构支撑载荷大小对薄壁工件模态参数的影响，用来判断加工过程中支撑力对加工稳定性的影响．此外，还有许多学者为抑制薄壁工件加工过程中的振动，对铣削加工工艺进行了深入的 研究[14-16]．

铣削加工过程中，准确估计薄壁工件铣削力大小是预测其变形和振动的关键．上述研究工作中，薄壁工件所受到铣削力通常按照铣刀所施加载荷大小来估计，很少考虑载荷和薄壁结构变形的相互作用．薄壁工件属于薄壁柔性结构，在加工过程中受铣刀载荷作用会发生弯曲变形．当受到铣刀再次作用时，其弯曲变形一般不会完全恢复，而是具有一定弯曲变形程度．这使得实际作用在薄壁工件上的铣削力大小随着薄壁工件的变形而变化，往往和施加在薄壁工件上的载荷相差较大[17]．此外，薄壁工件由于厚度很小，其动态特性通常会随着加工过程中材料去除和位置改变而变化．这些因素都使得薄壁工件加工过程中的变形和振动变得复杂，很难进行有效预测．

鉴于此，本文首先研究铣刀施加载荷和薄壁工件变形之间相互作用对铣削力的影响，建立相应的铣削力预估模型．在此基础上，考虑材料去除，建立镜像铣加工过程中薄壁工件动态力学模型，研究加工参数、支撑刚度和支撑阻尼对薄壁工件变形和振动的影响规律．最后通过对仿真模型和加工实验结果进行对比，验证仿真模型的准确性．

1 镜像铣加工中薄壁工件的变形和振动模型

1.1 镜像铣结构

薄壁工件镜像铣加工系统如图1所示，镜像铣加工系统由安装铣刀的加工机器人、安装支撑结构的支撑机器人和被加工薄壁工件组成．在镜像铣加工过程中加工机器人控制铣刀进给运动，对工件进行铣削加工．支撑机器人控制支撑结构移动，使支撑结构保持和铣刀镜像同步移动，对工件加工位置处提供支撑，以提高铣刀加工位置工件的局部刚度，抑制加工过程中薄壁工件的变形和振动．

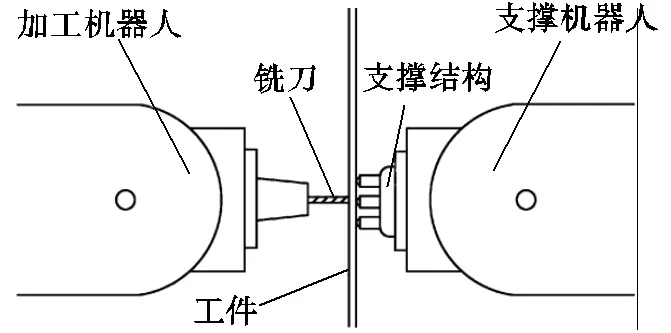
图1 镜像铣示意

1.2 铣削力的预估

薄壁工件的铣削过程中，由于薄壁工件和铣削力之间的相互作用，造成薄壁工件受到的实际铣削力大小和铣刀施加载荷相差较大．为了估计薄壁工件受到的实际铣削力大小，本文基于金属切削原理，建立考虑工件弯曲变形和铣刀施加载荷相互作用的薄壁工件铣削力预估模型．

在薄壁工件加工过程中，使用端铣刀进行铣削加工．端铣刀垂直于薄壁工件表面插入薄壁工件中，在平行于工件表面方向做进给运动，对薄壁工件进行铣削加工．因为被加工工件通常为大尺寸薄壁工件，铣刀轴向刚度远大于薄壁工件横向刚度，所以可以忽略铣刀变形，将铣刀视为刚体[14]．

在端铣刀施加载荷的计算中对端铣刀沿轴向方向进行离散，端铣刀铣削过程可看成多个d厚度铣刀微元铣削过程的叠加．铣刀微元上每个刀刃铣削过程可以简化为金属斜切过程，图2为端铣刀沿轴向方向离散示意和微元铣刀载荷几何模型．

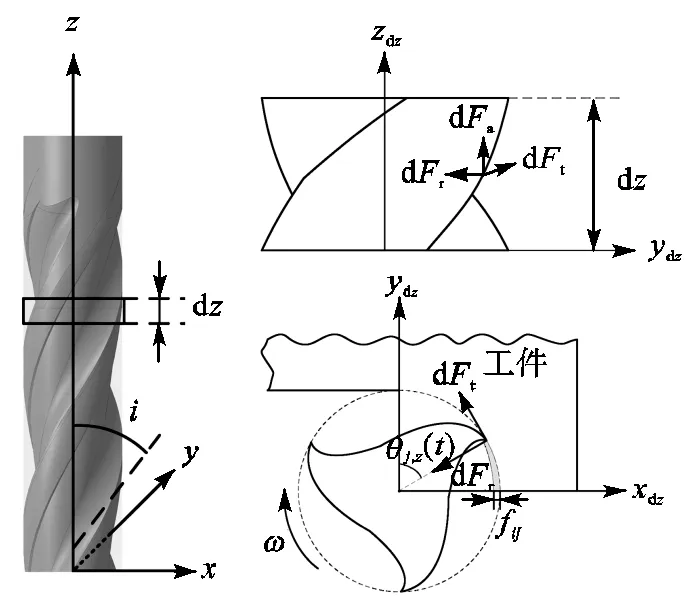
图2 端铣刀几何模型

在时刻高度为的微元第刃在切向、径向和轴向的切削力[18]分别为

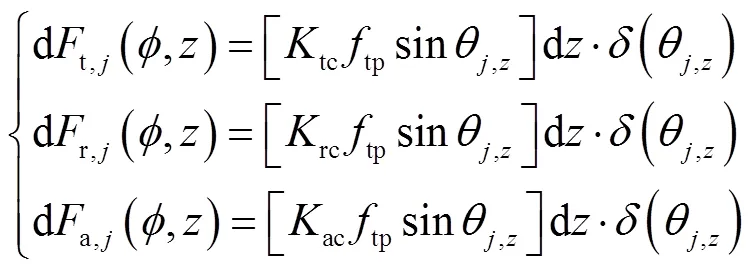
式中：为铣刀端面第1齿时刻角位置；为铣刀主轴角速度；θ,z为第齿刀刃上高度为的微元在时刻的角位置；为铣刀螺旋角；tp为铣刀每齿进给率；st和ex为铣刀刀刃切入角和切出角；式(2)用于判定切削刃微元是否处在铣削状态；tc、rc、ac分别为金属切削过程中切向、径向和轴向切削力系数，根据Armarego的金属斜切理论[18]，表达式为

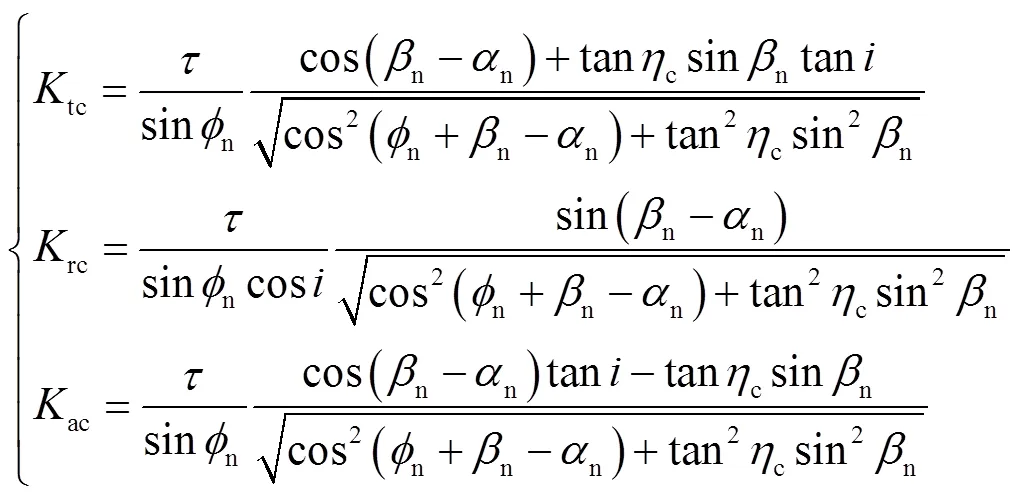
式中：为被铣削材料的剪切屈服强度；n为法向剪切角；n为金属斜切中法向前角；c为切屑流向方向；为金属斜切中倾斜角，在铣削中等于铣刀螺旋角；n为剪切角．

通过坐标变换，把切向、径向和轴向微元切削力转换到被加工工件的笛卡尔坐标系中，可得

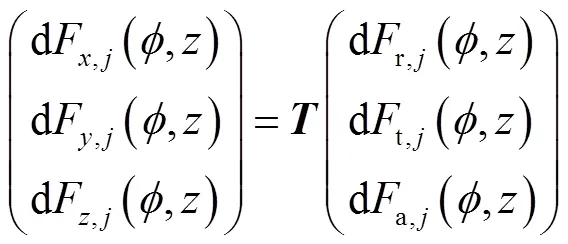
式中为坐标转换矩阵．

对微元切削力沿铣刀侧刃积分并进行叠加求和，得到铣刀施加载荷为

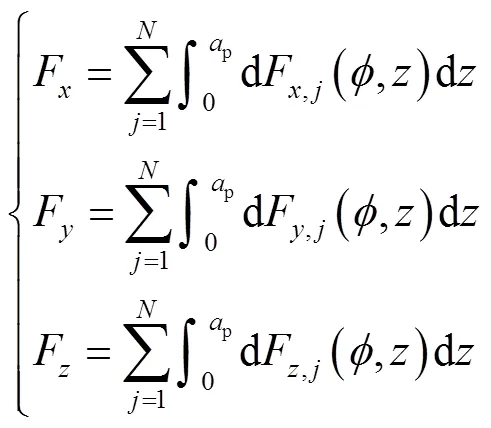
式中：为铣刀刀刃数；p为铣刀轴向切深．

当铣刀和被加工工件材料确定时，根据式(5)铣刀施加载荷可简化为主轴转速、进给率、轴向切深、径向切深等铣削加工参数和时间的函数，即

式中：t为主轴进给率；为主轴转速；e为铣刀径向切深．

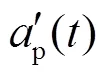
图3 薄壁工件和铣刀载荷的相互作用

薄壁工件在时刻受铣刀作用的瞬时铣削力大小为

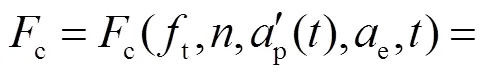
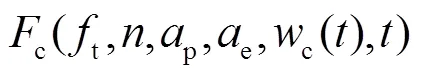
是否考虑薄壁工件变形和铣刀施加载荷之间相互作用得到的铣削力对比如图4所示．薄壁工件尺寸为1000mm×800mm×8mm，固定方式为对边夹紧，材料为6061铝合金，铣刀为直径16mm的3刃端铣刀，螺旋角为50°，主轴转速为5000r/min，进给率为2000mm/min，铣削力随进给距离的变化如图4所示．

由图4可得，在加工过程中铣削力实际大小随着薄壁工件变形而变化．因此，考虑加工过程中工件变形和铣刀施加载荷的相互作用，能够在很大程度上准确地预估薄壁工件所受到的实际铣削力，反映实际加工中的动态过程．

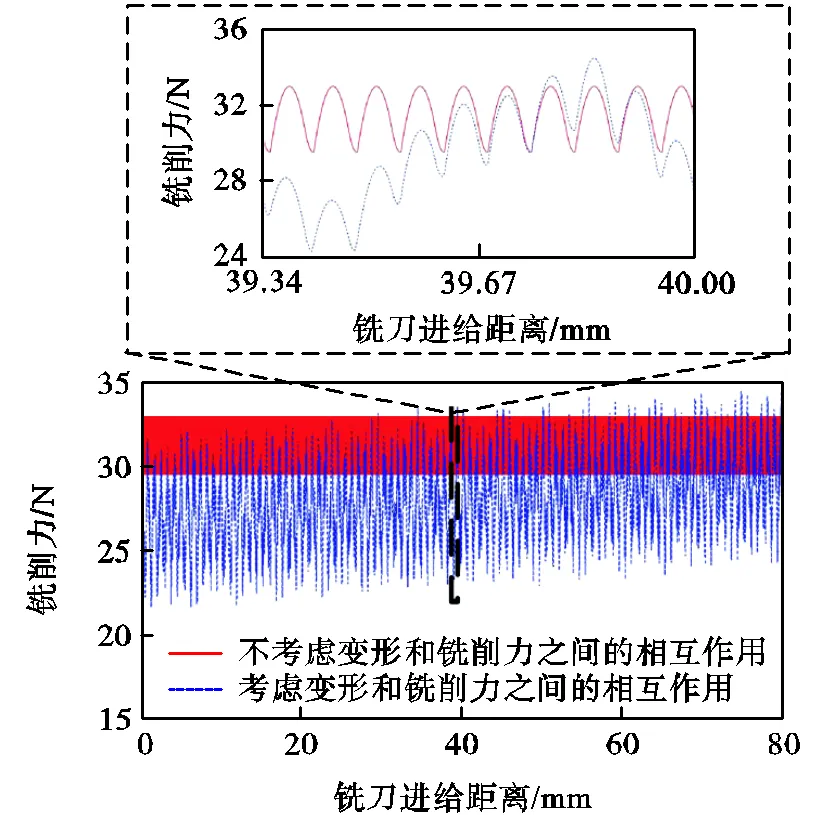
图4 考虑和不考虑薄壁工件变形和铣刀载荷之间相互作用的铣削力对比

1.3 支撑结构的影响

与传统支撑结构不同，柔性支撑结构由万向滚珠和气缸组合而成，气缸与气泵相连接可提供支撑，万向滚珠直接与工件表面相接触．柔性支撑结构固定在支撑机器人上，与铣刀相对薄壁工件保持镜像同步运动．多点柔性支撑结构示意如图5所示．

柔性支撑结构中，万向滚珠主要是将气缸提供的支撑力传递到薄壁工件上，考虑到气缸在运动中摩擦力和呼吸孔的影响，本文将气缸简化为弹簧阻尼，柔性支撑结构简化为弹簧阻尼器．

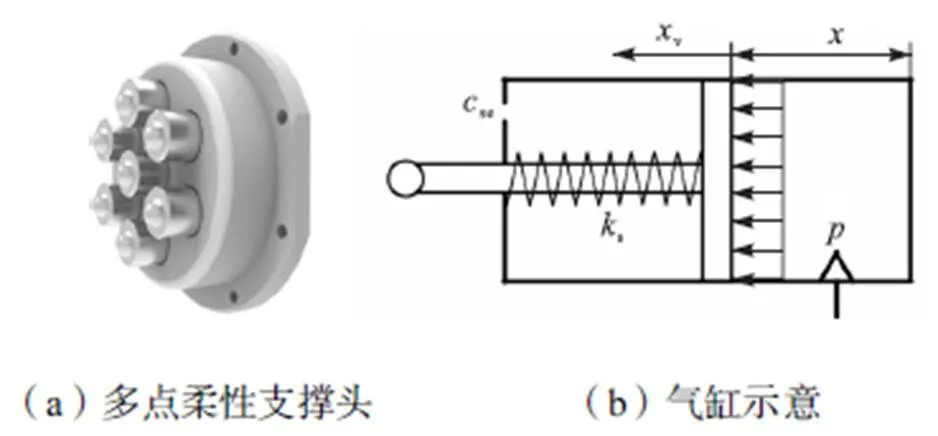
图5 多点柔性支撑结构

柔性支撑结构作用在薄壁工件的支撑力为

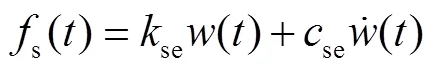
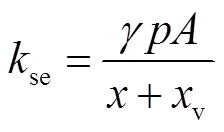
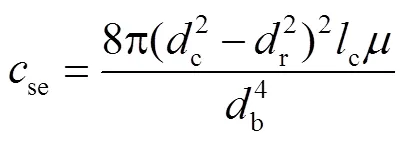
式中：se为等效支撑刚度；se为等效支撑阻尼，可由气缸参数和气缸气压计算得出[3]；为理想气体绝热系数；为气缸气压；为气缸无杆腔横截面积；为气体动力黏度系数；c为呼吸孔长度；c为气缸内径；r为气缸活塞杆直径；b为气缸呼吸孔直径．

忽略支撑结构与薄壁工件之间的摩擦力，只考虑支撑结构对薄壁工件横向支撑力．假设加工过程中支撑结构一直紧贴被加工工件表面，则薄壁工件受到的支撑为

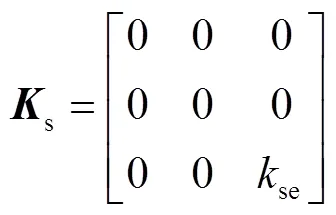
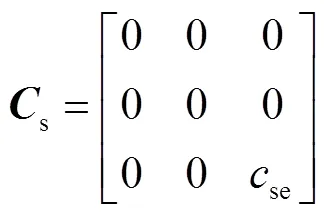
1.4 镜像铣加工过程中薄壁工件的变形和振动模型

随着加工过程中材料移除，工件质量、刚度等动态特性会发生相应变化，模态特性也随着位置改变而改变．因此，在薄壁工件铣削的动态模拟中，需要考虑载荷与支撑的镜像同步移动和材料的去除．

可用薄板模型描述加工过程中薄壁工件动态力学行为

式中()为薄壁工件在时刻受到的瞬时载荷．

在镜像铣削加工过程中，薄壁工件受到的载荷主要包括铣削力c()和支撑力s()．铣削力与支撑力沿着铣刀加工轨迹在薄壁工件上镜像同步移动，将铣削力和支撑力的具体表达形式代入式(13)，可得

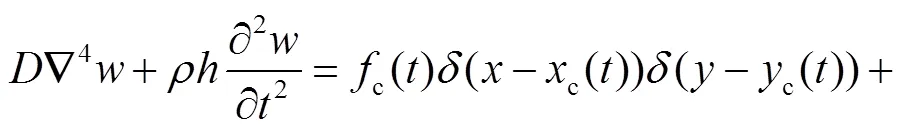
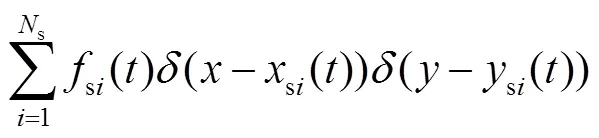
式中：()为迪利克雷函数；c()、c()为铣削力在时刻的瞬时位置；ci()、ci()为第个支撑头在时刻的瞬时位置；s为支撑头个数．铣削力和第个支撑头时刻的瞬时位置为

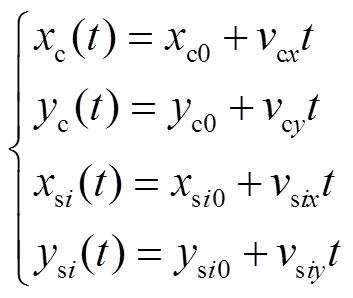
式中：c0、c0为铣削力的初始位置；cx、cy为铣削力的移动速度；si0、si0为第个支撑头的初始位置；six、siy为第个支撑头的移动速度．

使用MITC类型壳单元，通过有限元方法对式(14)进行瞬态求解，可较为准确地模拟薄壁工件瞬态响应[20]．运动方程为

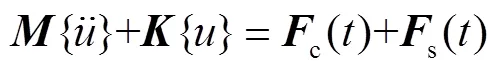
式中：为薄壁工件质量矩阵；为刚度矩阵；c()为时刻铣削力矩阵；s()为时刻支撑载荷矩阵．

为模拟加工过程中材料去除的动态影响，使用参数化函数定义有限元模型中壳单元厚度．被加工工件初始单元厚度为，经铣刀加工之后，单元厚度变为p．时刻薄壁工件质量矩阵和刚度矩阵分别为()和()，将式(7)、式(11)和式(12)代入式(16)，可得

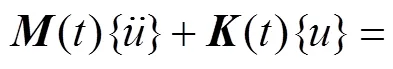
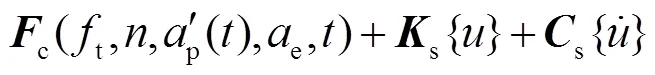
计算流程如图6所示．

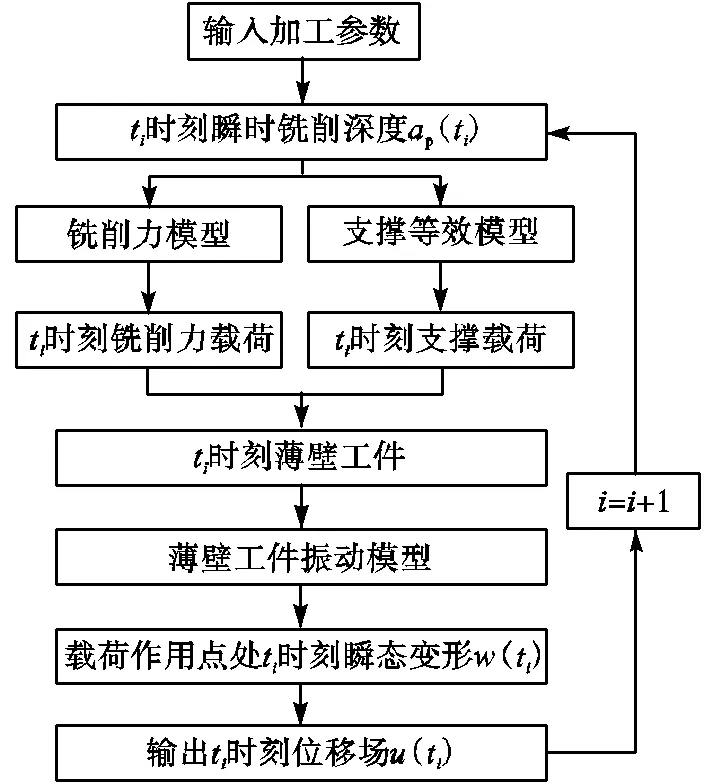
图6 计算流程

2 镜像铣加工过程中薄壁工件变形和振动的预测

2.1 不同支撑参数对薄壁工件变形和振动的影响

柔性支撑结构可以通过气缸变换以及气缸气压调整提供不同支撑刚度和支撑阻尼．下面对不同支撑刚度和支撑阻尼条件下薄壁工件镜像铣削加工过程进行模拟，研究支撑刚度和支撑阻尼对变形和振动行为的影响规律．

工件尺寸为1000mm×800mm×8mm，固定方式为对边固支，材料为6061铝合金，选择主轴转速5000r/min、进给率2000mm/min、直径为16mm的三刃端铣刀，轴向铣削深度为0.5mm铣刀从薄板中心点出发，沿与轴平行的方向以进给率t进行铣削加工．

多点柔性支撑结构可以对单一支撑头进行单独控制，也可以将所有支撑头并联进行统一控制．本文考虑了上述两种支撑方式．其中多点支撑情况下由于所有支撑头并联，每个支撑头支撑刚度和支撑阻尼都相等．

为了排除载荷移动到不同位置对变形和振动造成的影响，下文分析的数据均来源于载荷移动路径中的点，其坐标为(530mm，400mm)，如图7所示．

图8为单点支撑情况下支撑刚度和支撑阻尼对薄壁工件变形的影响．可以看出，当支撑阻尼相同时，支撑刚度和变形成正比关系，工件变形随着支撑刚度的增加而减小．当支撑阻尼低于1000N·s/m时，支撑阻尼对加工过程中变形无显著影响．

图9为单点支撑情况下支撑刚度和支撑阻尼对薄壁工件振动幅值的影响．可以看出，振动幅值随着支撑阻尼的增大而减小．当支撑阻尼小于500N·s/m时，振动幅值随着支撑阻尼的增加快速减小，当支撑阻尼达到500N·s/m后，增大支撑阻尼对振动幅值影响减小．

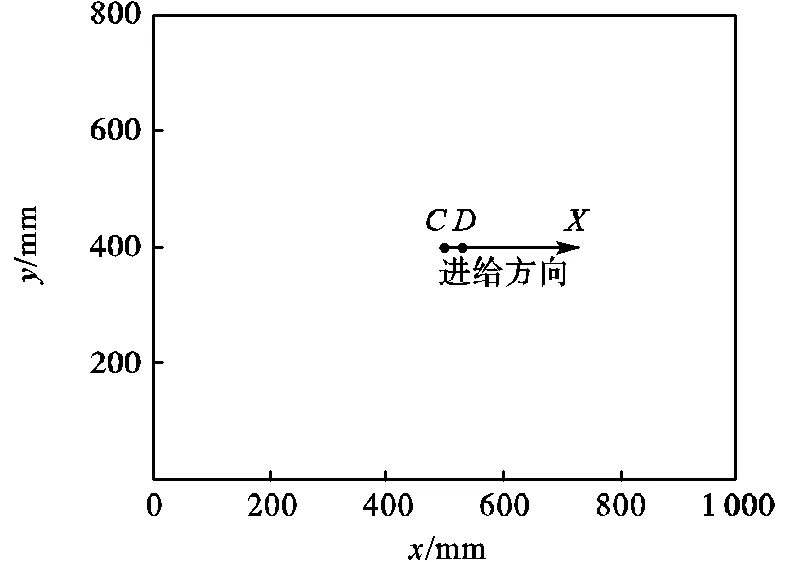
图7 进给方向

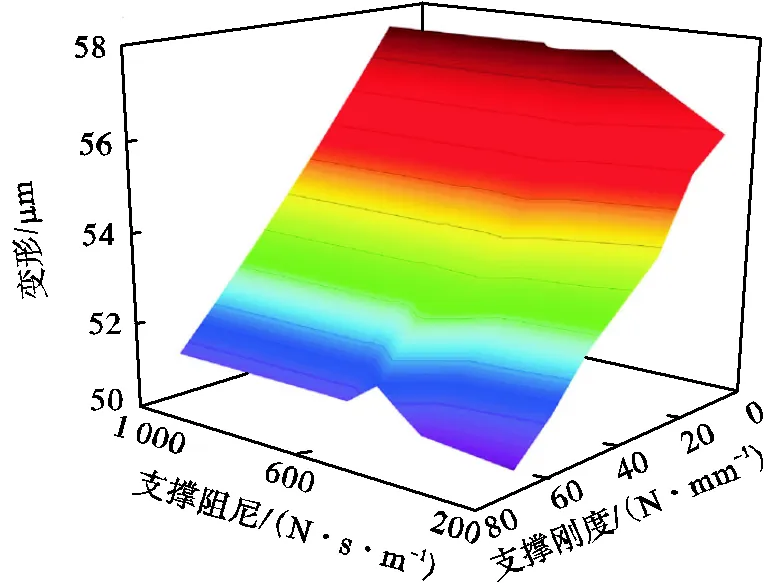
图8 单点支撑条件下支撑刚度和支撑阻尼对镜像铣削加工中薄壁工件变形的影响

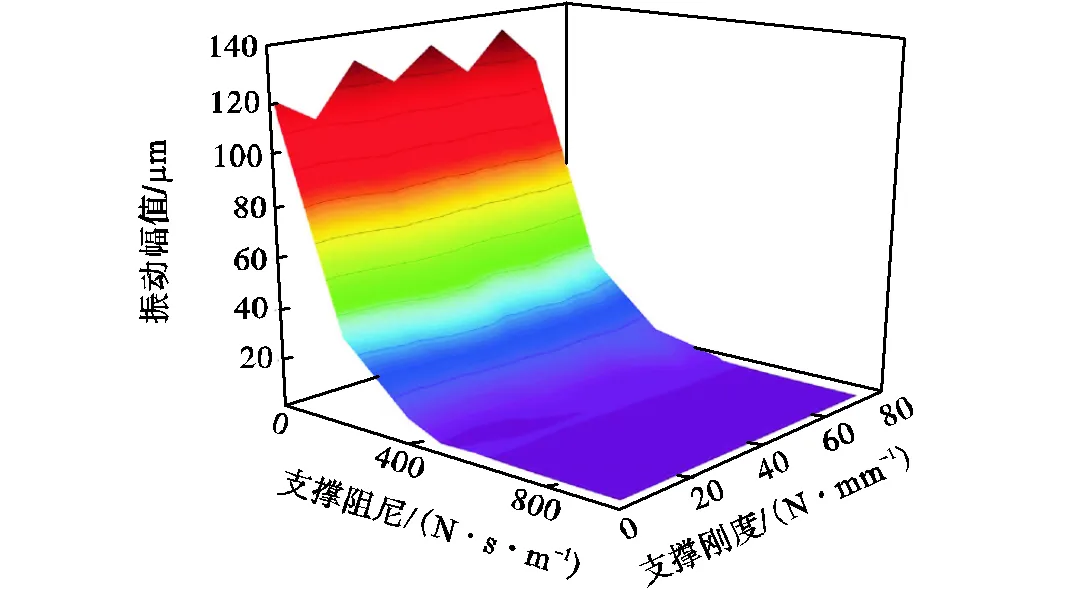
图9 单点支撑条件下支撑刚度和支撑阻尼对镜像铣削加工中薄壁工件振动幅值的影响

图10为多点支撑情况下单个支撑头支撑刚度和支撑阻尼对薄壁工件变形的影响．可以看出，多点支撑和单点支撑在不同支撑条件下对加工过程中薄壁工件变形的影响趋势一致，变形随着支撑刚度的增加而减小．

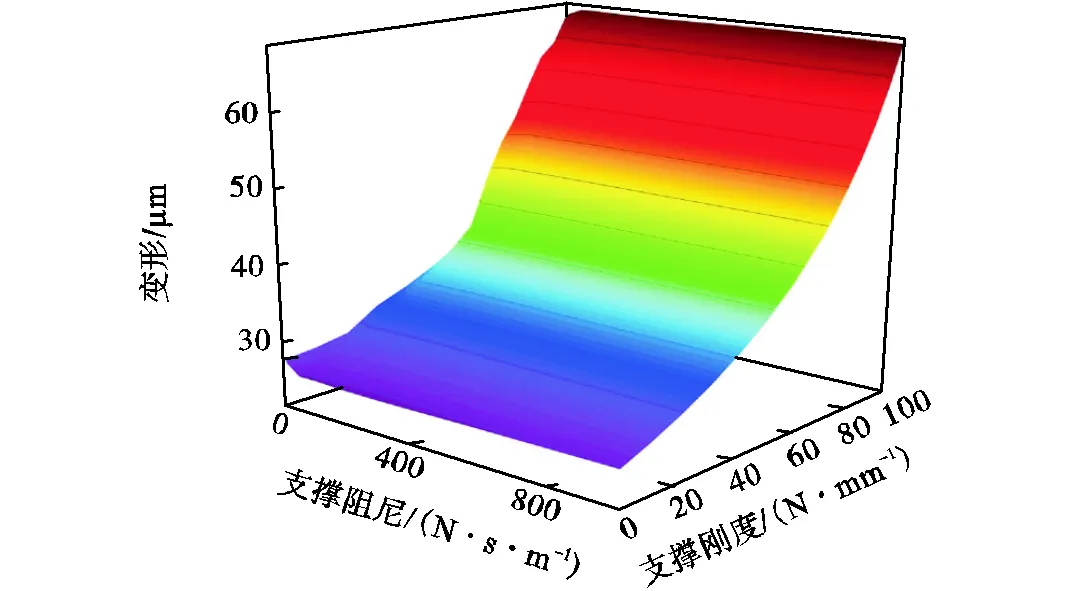
图10 多点支撑条件下支撑刚度和支撑阻尼对镜像铣削加工中薄壁工件变形的影响

图11为多点支撑情况下单个支撑头支撑刚度和支撑阻尼对薄壁工件振动幅值的影响．薄壁工件振动幅值随着支撑阻尼的增加而减小，当单个支撑头支撑阻尼小于50N·s/m时振动幅值随着支撑阻尼的增加而快速减小，支撑阻尼达到50N·s/m后，振动幅值随支撑阻尼的增加趋于稳定，增大支撑阻尼对振动幅值影响减小．

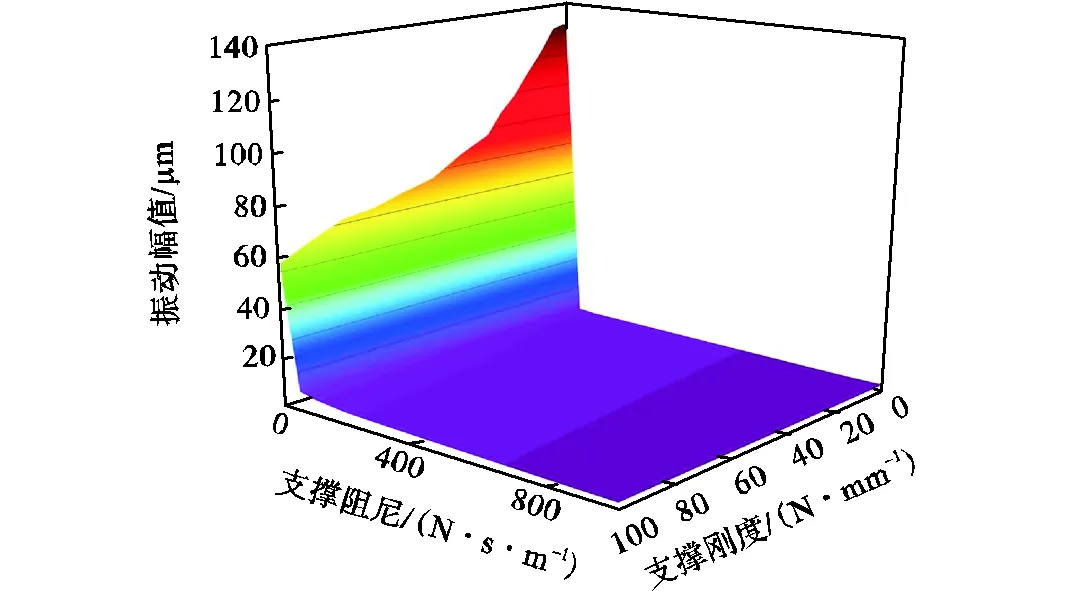
图11 多点支撑条件下支撑刚度和支撑阻尼对镜像铣削加工中薄壁工件振动幅值的影响

在加工参数固定时，单点支撑和多点支撑两种方式的支撑刚度和支撑阻尼对薄壁工件加工过程中变形和振动影响规律基本相同．变形随着支撑刚度的增加而减小，振动幅值随着支撑阻尼的增加而减小．多点支撑在单个支撑头支撑刚度和支撑阻尼与单点支撑相同时，对变形和振动的抑制作用更为明显．单点支撑情况下支撑阻尼达到500N·s/m，多点支撑单个支撑头支撑阻尼达到50N·s/m后，增大支撑阻尼对振动幅值的影响变小，振动幅值变化趋于稳定．因此，在镜像铣削加工过程中，为了减小变形可尽量选择大的支撑刚度．为了抑制薄壁工件振动，在单点支撑情况下支撑阻尼建议大于500N·s/m，多点支撑情况下单个支撑头支撑阻尼建议大于50N·s/m．

2.2 不同加工参数对薄壁工件的变形和振动的影响

除了支撑结构，铣刀加工参数的选择也会对加工中薄壁工件变形和振动产生显著影响．此处对加工过程中不同主轴转速和进给率的加工情况下薄壁工件变形和振动进行仿真预测．支撑结构根据第2.1节中分析采用多点支撑的支撑方式，单个支撑结构支撑刚度为50N/mm，支撑阻尼为50N·s/m，其余参数与第2.1节中一致．

图12给出了主轴转速和进给率对加工过程中薄壁工件变形的影响．结果表明，薄壁工件的变形随着主轴进给率的增加和主轴转速的减小而增加．

区县级电视台不重视优秀人才培养，在制作电视专题节目时往往缺乏相应的奖罚机制，没有将地区优点以及特色体现出来，在节目题材选择上存在缺乏吸引力的状况，其所使用的多媒体技术以及相应的节目制作技术还存在着很大的提升空间，在宣传方式和制作内容上都还需要进一步提高。

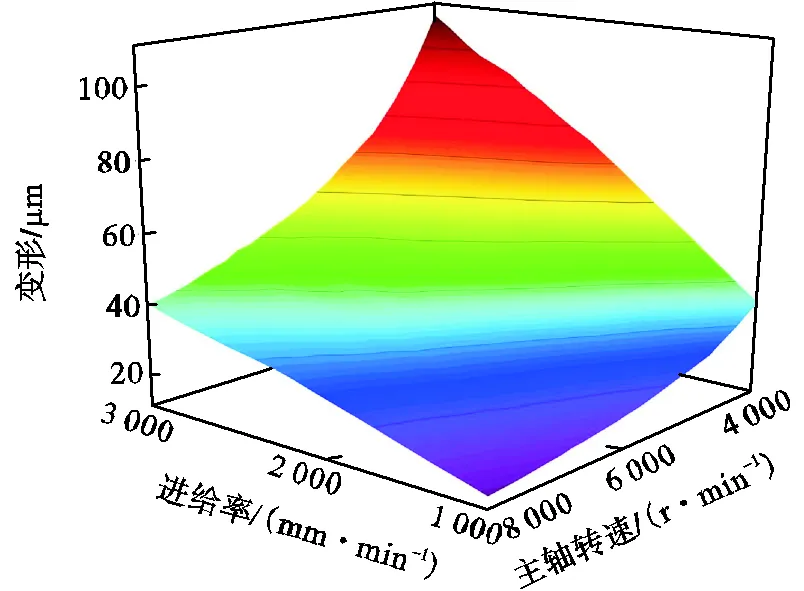
图12 主轴转速和进给率对镜像铣削加工中薄壁工件变形的影响

图13给出了主轴转速和进给率对加工过程中薄壁工件振动幅值的影响．可发现，振动幅值随着铣刀进给率的增加而增加，随着主轴转速的增加以波动形式减小．当主轴转速在3500r/min、5000r/min和7200r/min附近时，振动幅值明显减小，而在3000r/min、4500r/min和6200r/min附近时，振动幅值明显增大．振动幅值明显变大时，相对应的铣削力变化频率分别为150Hz、225Hz和310Hz．考虑到薄板固有频率为146Hz、205Hz和316Hz，上述结果表明此时薄壁工件在铣削力作用下发生了共振现象，导致振动幅值显著增大．

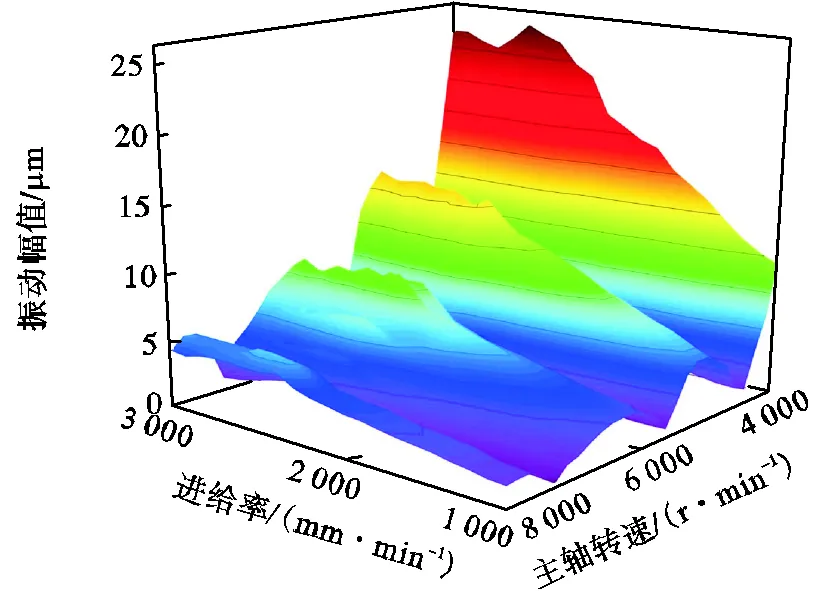
图13 主轴转速和进给率对镜像铣削加工中薄壁工件振动幅值的影响

上述对变形和振动的预测分析，有助于指导实际生产中加工参数的选择，有效减小薄壁工件加工过程中的变形和振动，以提高加工精度．

3 实验验证

薄壁工件镜像铣加工系统由两台TriMule-600五自由度混联机器人组成，两个机器人分别位于被加工薄壁工件的两侧．一个安装铣刀，一个安装支撑结构，二者在加工过程中进行镜像同步运动．实验装置如图14所示．

图14 镜像铣实验装置

图16为无支撑铣削薄壁工件动态响应实验和仿真位移结果对比．其中，无支撑加工过程中点处振动幅值的实验测量值为35.70μm，相应的仿真结果为36.37μm，二者相差仅为1.88%．

图17为多点柔性支撑镜像铣削加工薄壁工件动态响应实验和仿真位移结果对比．在多点柔性支撑镜像铣削加工中，点处振动幅值实验测量值为4.07μm，其仿真结果为4.25μm，二者相差仅为4.42%．

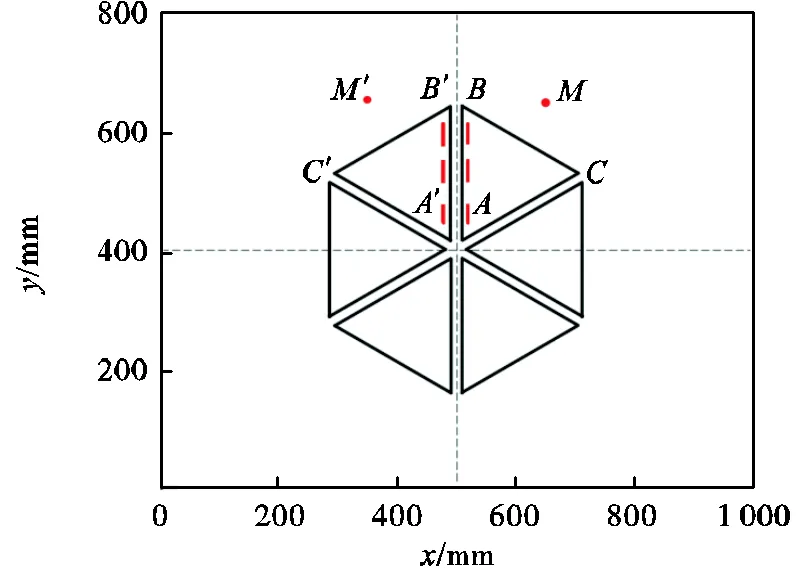
图15 实验铣削路径和测量点位置

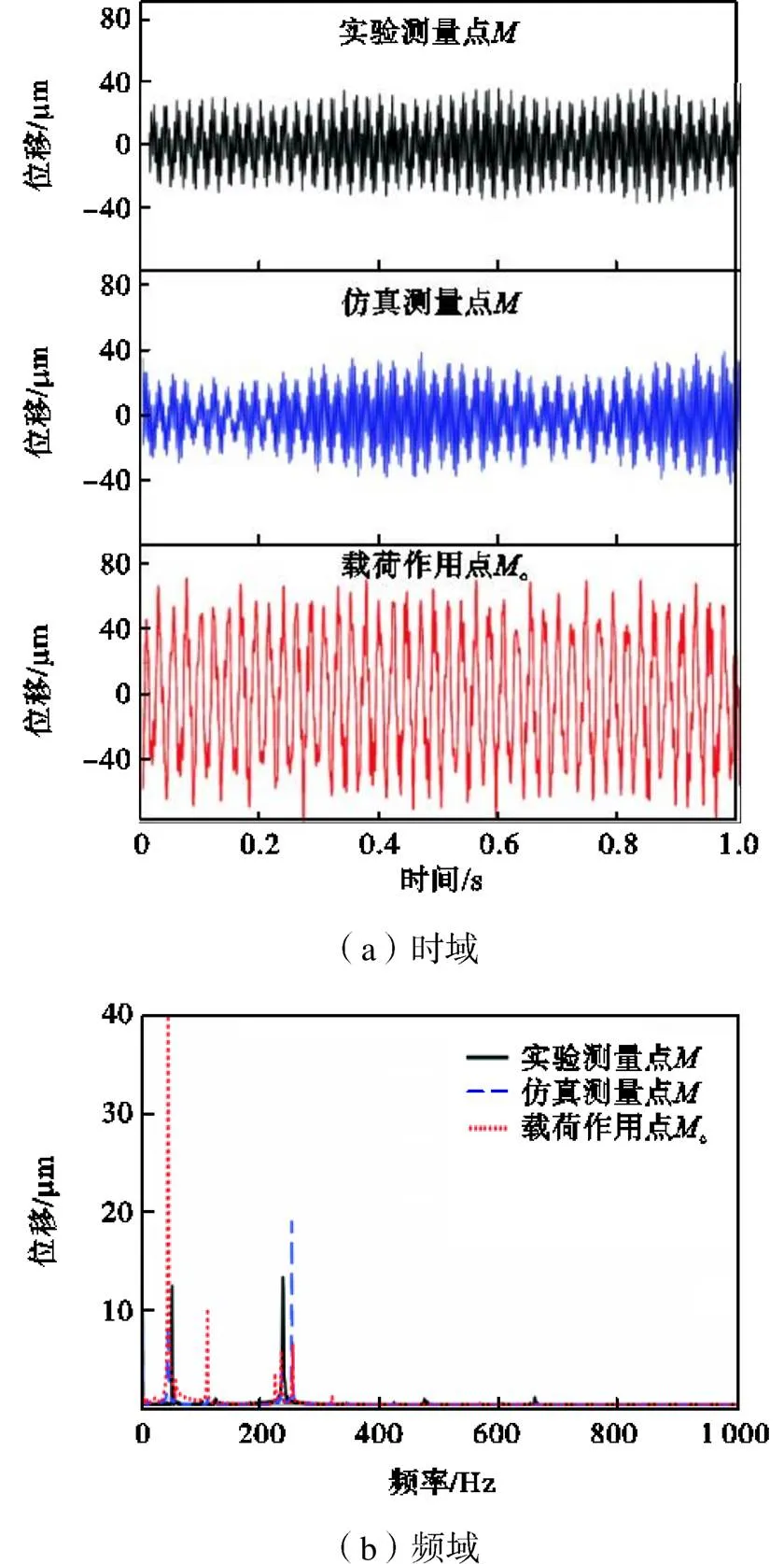
图16 无支撑铣削情况下实验和仿真位移对比

图17 多点支撑加工情况下实验和仿真位移对比

通过无支撑铣削和多点柔性支撑镜像铣削情况下实验和模型预测结果之间的对比，可发现实验和预测结果相差不超过5%．与文献[12]相比，本文提出的薄壁工件铣削加工过程中的动态力学模型，由于考虑了铣削力和薄壁工件变形相互作用以及加工过程中材料的去除，仿真结果与实验结果拟合更为精确．本文提出的模型能够更加准确地对镜像铣削加工过程中薄壁工件变形和振动行为进行仿真预测．

另外，在无支撑加工过程中，0～1000Hz的频域范围内薄板振动有多个峰值．而在镜像铣削加工过程中，振动峰值显著降低，其数量也明显减少．由此可见，柔性支撑结构对薄壁工件加工过程中的振动可起到明显抑制作用，有助于提高加工精度．

4 结 语

本文考虑加工过程中铣削力和工件变形之间相互作用，对薄壁工件受到的实际铣削力大小进行了估计．结合薄板小挠度理论和有限元法，建立了镜像铣削加工过程中薄壁工件动态力学模型．通过对不同支撑和加工参数条件下薄壁工件镜像铣削加工过程中动态响应的预测，研究了支撑刚度、支撑阻尼、主轴转速、进给率和支撑方式对薄壁工件变形和振动的影响规律．

仿真结果表明，薄壁工件变形随着支撑刚度的增加而减小，振动幅值随着支撑阻尼的增加而减小．单点支撑情况下支撑阻尼达到500N·s/m，多点支撑情况下支撑阻尼达到50N·s/m时，继续增大支撑阻尼对振动幅值的影响显著减小．当主轴转速在3000r/min、4500r/min和6200r/min附近时，铣削力的频率达到工件固有频率146Hz、205Hz和316Hz附近，振动幅值显著增大．薄壁工件镜像铣削加工过程中载荷作用点处振动幅值相比于直接铣削减小了92.02%．经过镜像铣削加工实验验证，仿真预测结果和实验数据相差小于5%，证明本文建立的镜像铣削薄壁工件动态力学模型能够较为准确地预测实际加工中薄壁工件的变形和振动．

本文工作对提高镜像铣削加工精度具有重要的参考意义．

［1］ Pas O，Serkov N. Developing an algorithm to control the accuracy of the milling of aerospace parts with cellular structure by using copying machine-tools with CNC of SVO type[C]//IOP Conference Series：Materials Science and Engineering. Moscow，Russian Federation，2019：1-5.

［2］ 鲍 岩，董志刚，朱祥龙，等. 蒙皮镜像铣削支撑技术的研究现状和发展趋势[J]. 航空学报，2018，39(4)：47-58.

Bao Yan，Dong Zhigang，Zhu Xianglong，et al. Review on support technology for mirror milling of aircraft skin[J]. Acta Aeronautica et Astronautica Sinica，2018，39(4)：47-58(in Chinese).

［3］ Xiao Juliang，Zhang Qingyue，Liu Haitao，et al. Research on vibration suppression by a multi-point flexible following support head in thin-walled parts mirror milling[J]. The International Journal of Advanced Manufacturing Technology，2020，106：3335-3344.

［4］ Zhang Li，Gao Weiguo，Zhang Dawei，et al. Prediction of dynamic milling stability considering time variation of deflection and dynamic characteristics in thin-walled component milling process[J]. Shock and Vibration，2016，2016：1-14.

［5］ Bao Yan，Kang Renke，Dong Zhigang，et al. Model for surface topography prediction in mirror-milling of aircraft skin parts[J]. International Journal of Advanced Manufacturing Technology，2018，95：2259-2268.

［6］ Li Zhao，Bao Yan，Kang Renke，et al. An advanced support method of aircraft skin mirror milling fluid lubricating support[J]. Materials Science Forum，2016，874：469-474.

［7］ Zhang Jin，Lin，Bin，Fei Jixiong，et al. Modeling and experimental validation for surface error caused by axial cutting force in end-milling process[J]. International Journal of Advanced Manufacturing Technology，2018，99：327-335.

［8］ Jiang Xiaohui，Wang Yifei，Ding Zishan，et al. An approach to predict the distortion of thin-walled parts affected by residual stress during the milling process[J]. The International Journal of Advanced Manufacturing Technology，2017，93：4203-4216.

［9］ Shi Jiahao，Song Qinghua，Liu Zhanqiang，et al. Formulating a numerically low-cost method of a constrained layer damper for vibration suppression in thin-walled component milling and experimental validation[J]. International Journal of Mechanical Sciences，2017，128/129：294-311.

［10］ Arnaud L，Gonzalo O，Seguy S，et al. Simulation of low rigidity part machining applied to thin-walled structures[J]. International Journal of Advanced Manufacturing Technology，2011，54：479-488.

［11］ Lan Jin，Lin Bin，Yan Shuai，et al. Application of mirror-milling machining system to suppress vibration in thin plate work-piece[C]// 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications(MESA). Auckland，New Zealand，2016：29-31.

［12］ Wang Weiqiang，Lin Bin，Guo Yu，et al. Dynamic simulation of mirror cutting[J]. International Journal of Advanced Manufacturing Technology，2019，103：4331-4340.

［13］ Bo Qile，Liu Haibo，Lian Meng，et al. The influence of supporting force on machining stability during mirror milling of thin-walled parts[J]. International Journal of Advanced Manufacturing Technology，2019，101：2341-2353.

［14］ Fei Jixiong，Lin Bin，Yan Shuai，et al. Chatter mitigation using moving damper[J]. Journal of Sound and Vibration，2017，410：49-63.

［15］ Irene Del Sol，Asuncion Rivero，Luis Norberto Lopez de Lacalle，et al. Thin-wall machining of light alloys：A review of models and industrial approaches[J]. Materials，2019(12)：1-28.

［16］代 煜，贾 宾，张建勋，等. 基于振动反馈的铣削机器人运动控制[J]. 天津大学学报(自然科学与工程技术版)，2020，53(10)：1093-1100.

Dai Yu，Jia Bin，Zhang Jianxun，et al. Motion control of milling robot based on vibration feedback[J]. Journal of Tianjin University(Science and Technology)，2020，53(10)：1093-1100(in Chinese).

［17］戚厚军，张大卫，蔡玉俊，等. 低刚度铣削工艺系统的弹性铣削力建模方法[J]. 天津大学学报，2010，43(2)：143-148.

Qi Houjun，Zhang Dawei，Cai Yujun，et al. Modeling methodology of flexible milling force for low-rigidity processing system during high speed milling[J]. Journal of Tianjin University，2010，43(2)：143-148(in Chinese).

［18］ Yusuf A. Manufacturing Automation-Metal Cutting Mechanics，Machine Tool Vibrations，and CNC Design[M]. United Kingdom：The Press Syndicate of The University of Cambridge，2000.

［19］李士鹏，田利成，秦旭达，等. 基于螺旋铣孔柔性切削力建模的孔径误差补偿[J]. 天津大学学报(自然科学与工程技术版)，2017，50(2)：147-153.

Li Shipeng，Tian Licheng，Qin Xuda，et al. Error compensation based onflexible cutting force model in hole helical milling process[J]. Journal of Tianjin University(Science and Technology)，2017，50(2)：147-153(in Chinese).

［20］ Jun H. New higher-order triangular shell finite elements based on the partition of unity[J]. Structural Engineering and Mechanics，2020，73：1-16.

Prediction of Deflection and Vibration of Thin-Walled Workpiece During Mirror-Milling Process

Wang Jianshan，He Tianyu，Xiao Juliang，Liu Haitao

(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

Mirror-milling is considered to be one of the most effective methods for machining large thin-walled workpieces，which are commonly used in aerospace and other important fields. During the mirror-milling process，the thin-walled workpieces’ deflection and vibration are the main factors that distinctly affect the machining accuracy. Thus，the effective prediction of the deformation and vibration of thin-walled workpieces is crucial for optimizing the parameters and improving the accuracy. Based on the principles of metal cutting，this study develops a model accounting for the interactions between the thin-walled workpiece deflection and the applied load to predict the actual milling force. Based on the Kirchhoff plate theory and finite element method，a dynamic model is developed to simulate the deflection and vibration of thin-walled workpieces during the mirror-milling process. The effects of support stiffness，support damping，spindle speed，and feed rate on the deflection and vibration of thin-walled workpieces have been investigated. The deformation of the thin-walled workpiece decreases with increased support stiffness，and the vibration amplitude decreases with increased support damping. Mirror-milling tests of the thin-walled workpiece made of aluminum alloy 6061 are conducted to verify the developed dynamic model. Both the time and frequency-domain signals of displacement are compared with those from the tests using the established model. The differences between the predicted results and those obtained from the experiment at the vibration data collection point are less than 5%，demonstrating the effectiveness of the proposed model in predicting and analyzing the deflection and vibration of the thin-walled workpiece during mirror-milling. Under the action of a multipoint flexible following support head，the vibration amplitude of the workpiece is reduced from 71.61μm to 5.71μm. The results show that the flexible following support head can effectively suppress the vibration. The study is helpful in improving the machining accuracy of mirror-milling.

mirror-milling；thin-walled workpiece；deflection；vibration；prediction；support；milling parameters

TK448.21

A

0493-2137(2022)03-0263-10

10.11784/tdxbz202101048

2021-01-21；

2021-04-27.

王建山（1977—  ），男，博士，教授，wangjs@tju.edu.cn.

肖聚亮，tianjinxjl@163.com.

国家自然科学基金资助项目(91948301，91648202).

Supported by the National Natural Science Foundation of China(No. 91948301，No. 91648202).

(责任编辑：金顺爱)