善用经典模型探究 提高学生物理核心素养
——2022年高考全国乙卷第25题为例
2022-11-30广东褚祝文
广东 褚祝文
核心素养提出,“深度学习”成为课堂教学的热门话题,同时为课堂教学改革提供新的思路和方向。“深度学习”就是在教师指导下,给学生提出具有挑战或创新性的物理学习主题,让学生积极参与、全身心投入获得必备品质和关键能力的学习过程。本文以2022年高考全国乙卷第25题为例,对教师在平常教学中如何利用经典模型进行深度挖掘,多角度设计了一些真实性、研究性或开放性的问题,以期培养学生多视角思考和提出问题的习惯,提高学生高阶思维和创新能力。
1 原题解析
如图1,在光滑水平面上静止一质量为m的物块A与轻质弹簧连接;物块B以一个初速度向A运动,从t=0时与弹簧接触,到t=2t0时与弹簧分离,完成第一次碰撞,物块A、B的v-t图像如图2所示。A、B第一次碰撞后,物块A滑上粗糙斜面,然后滑下,与一直在水平面上运动的物块B第二次碰撞,碰撞之后A再次滑上斜面,第二次达到的最高点与前一次相同,斜面与水平面光滑连接。已知从t=0到t=t0这段时间内,物块A运动的距离为0.36v0t0。斜面倾角为θ(sinθ=0.6)。碰撞过程中弹簧始终处于弹性限度内。求:

图1

图2
(1)第一次碰撞过程中,弹簧弹性势能的最大值Epmax;
(2)第一次碰撞过程中,弹簧压缩量的最大值Δx;
(3)物块A与斜面间的动摩擦因数μ。
【解析】(1)由题意分析,当A、B速度相等时,弹簧弹性势能最大,对A、B系统有
mB(1.2v0)=(mB+m)v0①

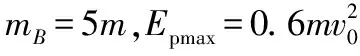
(2)解法一:同一时刻,弹簧对A、B的作用力分别是作用力与反作用力,由F=ma得aA=5aB,则物块B的运动可以看作初速度为1.2v0的匀速运动和初速度为0、加速度为aB的反方向匀变速直线运动的合运动。将初速度为0,加速度为aB的反方向在0到t0时间内运动的距离设为xC。
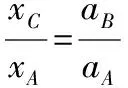
物块B的位移xB=12v0t0-xC=1.128v0t0,弹簧最大压缩量 Δx=xB-xA=0.768v0t0

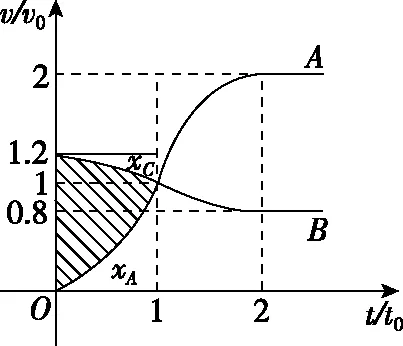
图3
解法三:把A、B看成一个系统,则质心做匀速运动,对系统有
mBvB+mvA=(mB+m)v0
则mB∑vBΔt+m∑vAΔt=(mB+m)∑v0Δt
解得mBxB+mxA=(mB+m)v0t0
且Δx=xB-xA
解得Δx=0.768v0t0
(3)设A第一次滑下斜面的速度为vA,A、B发生第二次弹性碰撞有
mvA-mB(0.8v0)=m(-2v0)+mBvB
解得vA=v0
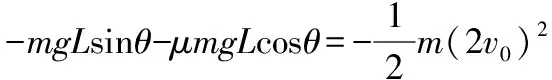
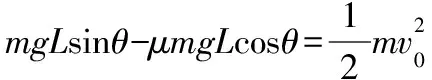
解得μ=0.45
2 试题评析
2.1 遵循《新课标》,突出基础性与综合性的考查
《普通高中物理课程标准(2017版2020年修订)》(以下简称《新课标》)与2003版《课标》相比,《新课标》把“碰撞”的内容改为“弹性碰撞和非弹性碰撞”,通过探究,了解弹性碰撞和非弹性碰撞的特点。本题在A与B两物体发生弹性正碰的经典模型中,巧妙加入一个轻质弹簧,通过放大弹性碰撞的形变量,让学生探究弹性碰撞的过程,分析受力、加速度、速度、机械能和动量如何变化及整个相互作用过程所遵循的物理规律;利用“追击相遇模型”分析两物体速度相等时,弹簧弹性势能最大,并用v-t图像描绘A、B相互作用的物理过程。让学生回顾弹性碰撞模型,遵循《新课标》,很好地考查学生推理论证能力、模型构建能力和分析综合应用能力。
2.2 立足物理核心素养,突出对解决问题能力的考查
(2)(3)问从A、B物块发生第一次碰撞,A物块滑上斜面然后下滑,两物块发生第二次碰撞,而后A物块沿斜面再次上滑到相同高度。这是一道多过程的物理综合题,很好地考查学生的理解能力、信息处理能力、推理论证能力和分析综合能力。此题使物理概念和规律在问题解决的过程中进一步得到内化、提升和升华。特别是第(2)问中已知第一次碰撞刚开始t0时间内物块A运动的距离为0.36v0t0,求此时弹簧压缩量的最大值;此时物块B不是做匀减速运动,不能用直线运动规律来求物块B的位移,学生从弹簧对A、B作用力分别是作用力与反作用力入手,联想出A与B碰撞加速度和速度的关系,运用合成法、类比法、图像法、联想法等多种方法求物块B在从t=0到t=t0时间内的位移,最后求出弹簧最大压缩量,很好地考查学生质疑创新能力及运用物理知识解决实际问题的能力,通过一题多解,让学生感受物理学科的魅力及多样性,引导学生从“物理解题”走向“解决实际问题”。
3 试题拓展
【拓展一】其他条件与原题相同,A物块没有连接轻弹簧,让A、B两物块发生碰撞,没有物块A、B的x-t图像,已知mB=5m,求:
(1)物块A、B发生第一次碰撞后A、B可能速度?
(2)若A、B第一次碰撞后,A获得最大速度,物块A滑上粗糙斜面,然后滑下,与一直在水平面上运动的物块B再次发生相同的碰撞,而后A再次滑上斜面,第二次达到的最高点与前一次相同,斜面与水平面光滑连接。求物块A与斜面间的动摩擦因数μ。
【解析】(1)如果A、B物块发生弹性碰撞,A物块加速运动的时间长,当A速度最大时,B物块的速度最小;如果A、B发生完全非弹性碰撞,A物块加速运动的时间最短,当A速度最小时,B物块的速度最大。
若A与B发生完全非弹性碰撞,则
5m(1.2v0)=(5m+m)v1
解得v1=v0
若A与B发生完全弹性碰撞,则
5m(1.2v0)=5mv1+mv2
解得v1=0.8v0,v2=2v0
因此,A、B物块的速度范围分别为v0≤vA≤2v0,0.8v0≤vB≤v0
(2)要使A第一次碰撞后速度最大,则A与B发生弹性碰撞,其余解答与原题第(3)问相同。
【拓展二】其他条件与原题相同,A物块没有连接轻弹簧,让A、B两物块(可以看作质点)发生弹性碰撞,已知物块A与斜面间的动摩擦因数μ=0.45,试求A物块初始位置与斜面底端之间的距离L需满足的条件。(重力加速度为g)
【解析】若保证物块A与一直在水平面上运动的B发生第二次弹性碰撞,则A、B两物块至少刚好运动至斜面底端发生第二次弹性碰撞。
设A物块沿斜面上滑和下滑的加速度分别为a上和a下,根据牛顿第二定律,则
上滑时mgsinθ+μmgcosθ=ma上
下滑时mgsinθ-μmgcosθ=ma下
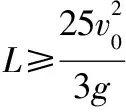
【拓展三】其他条件与原题相同,物块A第二次滑到斜面最高点与前一次相同时,恰好与正以速度为v0匀速下滑的C物块发生碰撞(没有粘连在一起),碰撞后两者动量相同,已知物块A与斜面间的动摩擦因数μ=0.45,求物块A再次滑至水平面时的速度范围?
【解析】题目隐含一个条件,即不知道A、C两物体发生什么碰撞,也没有已知C的质量,若A、C发生完全非弹性碰撞,碰撞后A的速度最小,若要符合条件,此时C的质量最小为M,则A与C发生完全非弹性碰撞
Mv0=(M+m)v
Mv=mv

若A、C发生弹性碰撞,碰撞后A的速度最大,若要符合条件,此时C的质量最大为M,则
Mv0=Mv1+mv2
Mv1=mv2
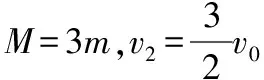
A物块上滑过程有
A物块下滑过程有
解得A物块再次滑至水平面时的速度为
【拓展四】其他条件与原题相同,在物块B的左侧有质量为M(未知)物块C正以速度v0向右做匀速运动,当A、B发生弹性碰撞后,此时C没有与B发生碰撞,迅速把物块B取走。已知物块A与斜面动摩擦因数为μ=0.45,求C与A发生第一弹性碰撞后,物块A第二次到达的最高点离斜面底边可能的最大距离(斜面足够长)。
【解析】A物块沿斜面上滑过程有
A物块沿斜面下滑过程有
解得v1=v0
A、C发生弹性碰撞,则
Mv0-mv0=Mv1+mv2
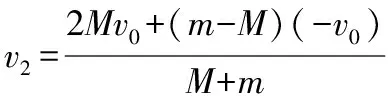
M取无限大,此时物块A第二次碰撞速度最大,则
v2=3v0
4 教学启示
4.1 注重教材经典模型挖掘,引导学生深度学习
《新课标》着重强调高中物理课程注重体现物理学科的本质,培养学生物理核心素养。自主学习能力被视为核心素养的本质与核心,且特别强调批判性思维、反思性思维、有效合作和沟通能力,这就需要教师对教材中的经典模型进行深度挖掘,创设学生积极参与、乐于探究、善于实验、勤于思考的学习情境;需要教师利用经典模型,多角度设计问题,多设计开放性、与实际生活联系紧密的问题,利用多样化的教学方式和现代信息技术,让学生探究、实验验证、推理论证,通过实际问题探究促进学生对物理观念的内化、提升和升华,培养和发展学生的自主学习能力,让深度学习真正发生。
4.2 注重“新教材”习题的挖掘,培养学生质疑、创新能力

