简谐运动物理量的理论推导与应用

云南 张保雷 胡家光

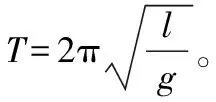
1 基本概念

1.1 简谐运动的定义

如果质点的位移与时间的关系遵从正弦函数的规律，即它的振动图像(x-t图像)是一条正弦曲线，这样的振动叫做简谐运动，简谐运动位移与时间的关系的表达式为x=Asin(ωt+φ0)，式中A是振幅，ω为圆频率，t为时间，φ0为初相位。

1.2 简谐运动的受力特征

简谐运动的受力特征为F=-kx，其中F为指向平衡位置的回复力，也叫谐振特征力；x为振动质点偏离平衡位置的位移；k为恢复系数，由振动系统自身性质决定；“-”表示F与x方向相反。由牛顿第二定律F=-kx=ma，可知简谐运动为变加速运动。

1.3 简谐运动的周期

2 理论探究

2.1 简谐运动的位移、速度、加速度

由简谐运动位移与时间的关系

x=Asin(ωt+φ0) ①

解得简谐运动质点的速度

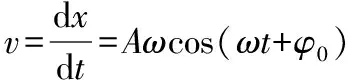
当cos(ωt+φ0)=1时，简谐运动质点的速度最大，此时x=Asin(ωt+φ0)=0，即质点通过平衡位置的速度最大，最大值为vM=Aω；

简谐运动质点的加速度

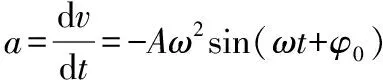
当sin(ωt+φ0)=1，此时x最大，即质点位于距平衡位置位移最大处，且加速度最大，最大值为aM=Aω2；

由①②③式，可知简谐运动质点的位移、速度、加速度与时间的关系均遵从正弦函数的规律。

2.2 简谐运动的回复力

根据牛顿第二定律，可得简谐运动质点的受力

F=ma=-mω2Asin(ωt+φ0) ④

由④式可知简谐运动质点的受力与时间的关系均遵从正弦函数的规律。

由①④式易得简谐运动质点的受力

F=-mω2Asin(ωt+φ0)=-mω2x=-kx⑤

其中k为恢复系数，k的大小由振动系统自身性质决定，振动系统不改变，则振动过程中k保持不变，即做简谐运动的质点所受作用力大小与位移成正比，方向与位移相反，该力始终指向平衡位置，物理学中按效果将其命名为回复力。从简谐运动的受力特征出发是证明某运动为简谐运动简单、有效的常用方法。

2.3 简谐运动的周期

由⑤式可得k=-mω2⑥

其中m为振子质量，k为振动系统的恢复系数，此式从简谐运动的定义式出发推理而得，适用于任何简谐运动周期的计算。

2.4 简谐运动的能量

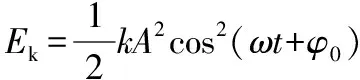
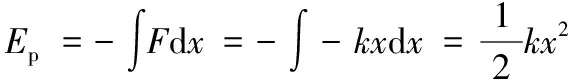
结合①⑨式，简谐运动系统的势能为

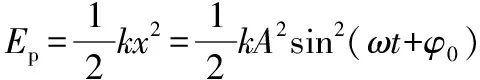
由⑧⑩式可得简谐运动系统的动能与势能之和

3 常见简谐运动的实例分析

3.1 弹簧振子

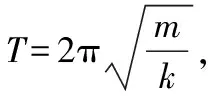
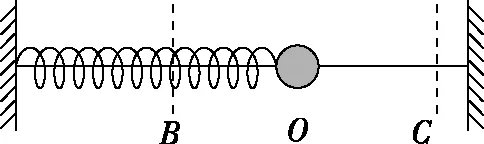
图1

3.2 单摆

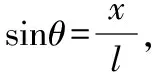
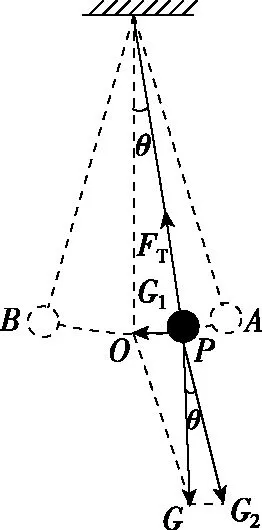
图2

4 非常见简谐运动的实例分析

如图3所示，电荷量分别为4q和-q的小球A、B固定在水平放置的光滑绝缘细杆上，间距为d。若杆上套一带正电的小环C(图中未画出)，带电体A、B和C均可视为点电荷。若小环C所带的电荷量为-q，将小环拉离平衡位置一小段位移x(|x|=d)后由静止释放，计算小环C回到平衡位置所用时间。

图3

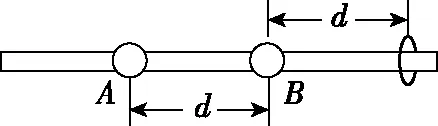
图4

5 结语

通过上述对简谐运动位移、速度、加速度、周期和能量的理论探究，发现简谐运动各物理量有着深层次的内在联系，只要确定了恢复系数，相对复杂的振动周期和能量就迎刃而解了。如果师生能经历上述理论探究过程，不仅可以对简谐运动有深入系统地认识，也能体验科学探究的方法和体会理论探究的乐趣，也是优秀学生成长的一条有效途径。