斜拉桥拉索损伤对桥梁结构静力特性的影响分析

严超群， 穆江飞

(杨凌职业技术学院 交通与测绘工程学院， 陕西 杨凌 712100)

0 概 述

随着社会经济的高速发展，我国交通量也在急剧增长，越来越多的桥梁应运而生。由于斜拉桥有较强的跨越能力和较为合理的经济特性，故在很多跨海跨江跨河工程上都采用此类桥作为主体工程。然而斜拉桥属于受力复杂的高次超静定结构，由主梁、斜拉索和索塔三部分构成，而斜拉索作为连接主梁与索塔的重要组成部分，其能否合理传力直接决定斜拉桥的受力性能。由于桥梁的施工误差以及在运营过程中养护管理工作的不完善，在运营过程中斜拉索不可避免会出现一些病害特征，如拉索出现锈蚀、松弛和断索等结构病害[1-2]，进而影响到主梁和主塔的受力状况，导致结构为达到新的平衡而应力重分布，严重影响结构的安全性能以及造成了较为恶劣的社会影响。据养护单位统计发现，大部分斜拉桥拉索都存在不同程度的损伤，这使得结构的健康状态评估存在漏洞。因此，为保证运营过程中的斜拉桥处于理想受力状态，做到对结构进行动态实时健康监测与评估，研究斜拉索在不同程度损伤和不同位置损伤情况下对结构静力特性的影响十分有必要。

1 斜拉索索力的测试方法

目前斜拉索索力的测试方法主要有：频率法、振动波法、液压千斤顶的压力表测试法、压力传感器测试法等[3]，各种检测方法的原理及适用性都不尽相同。为了系统地比较各种方法的优劣性，现将各种检测方法的适用性和局限性进行列表比较，如表1所示。

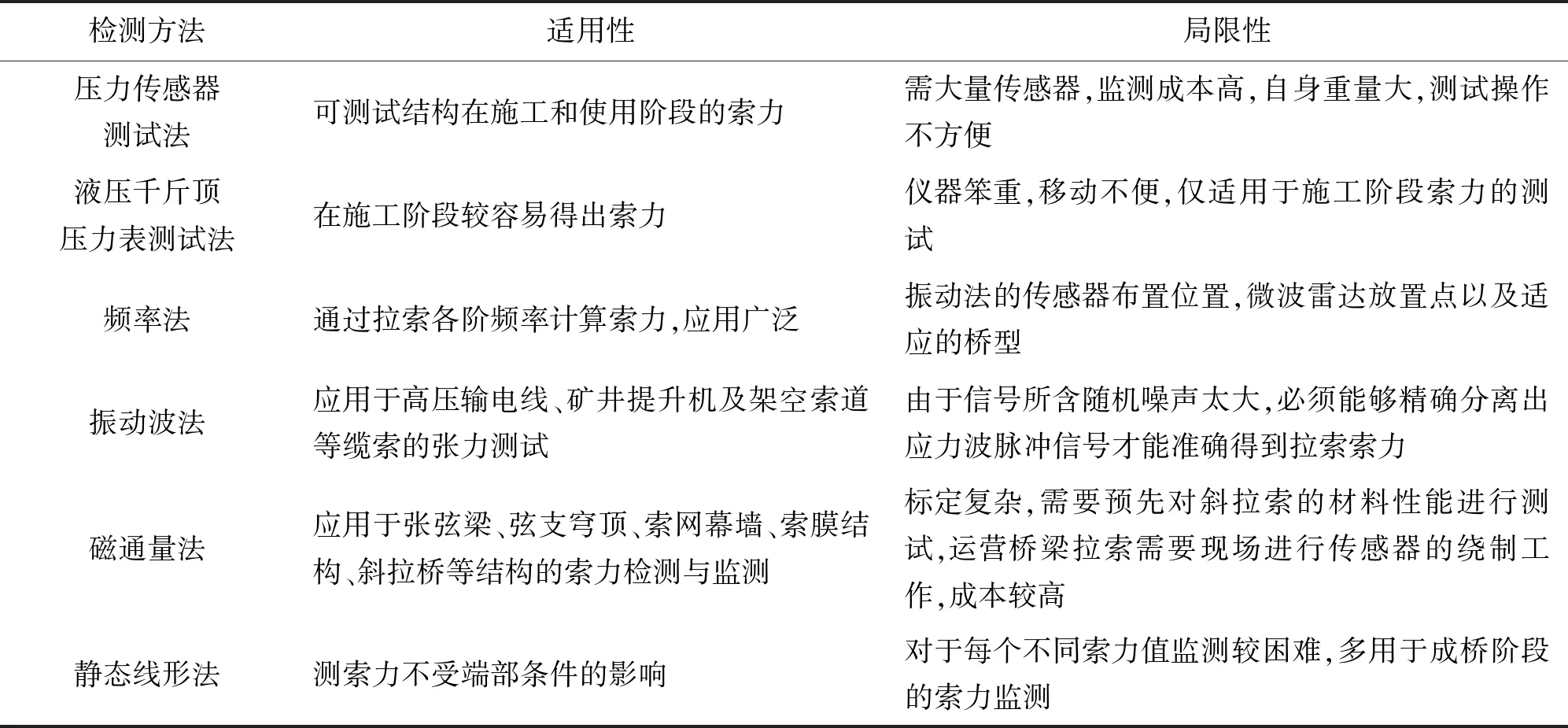
表1 索力检测方法适用性和局限性比较

其中，在工程索力常规检测中频率法最为常用，可分为有振动的接触式和采用微波雷达法的非接触式两种。

(1)振动法。振动法的测试原理主要是通过在索体上布置加速度传感器，采用人工激振或随机的方式获取斜拉索的振动信号，将之转换成电信号和数字信号，并对采集数据进行频域分析以得到拉索的各阶固有频率fn，再通过频率与索力的换算关系获得该拉索的索力值，具体关系式如下：

式中：T为索力；fn为n阶振动频率数；l为索长。

(2)微波雷达法。微波雷达法是基于干涉测量技术实现索力受力状态测试的一种方法。微博雷达发射微波信号，通过不断发射和遇拉索后的反射，获得一系列的变化相位以计算拉索的振动变化位移，位移时程曲线经过时频变换计算出振动频率，从而计算拉索索力。

虽然有较多方法可以检测斜拉索的索力，而且近年来无损检测技术在过来的应用也越来越广泛，出现了磁漏检测法、声发射检测法和索力检测[3]等方法，然而斜拉索数量较多，目前还达不到对每根拉索的受力状态进行动态实时监测，也就无法监测到整个桥梁结构的受力状态。因此，为便于后期更方便、更快捷地找到拉索损伤位置并及时调整更换拉索，以某运营斜拉桥为研究背景，分别在不同荷载工况下研究拉索损伤与主梁线形、拉索索力之间的变化规律。

2 工程背景

主体结构模型为双塔三跨预应力混凝土斜拉桥，采用双索面半漂浮结构体系。跨径组合为100 m+220 m+100 m，桥面总宽为31 m，设计双向六车道，顶面设双向2%的横坡。全桥使用40对钢质斜拉索，索面辐射型布置。本文通过Midas/Civil有限元软件对该斜拉桥进行实体建模分析，斜拉桥拉索采用桁架单元模拟，主梁和主塔均用梁单元模拟。主体结构模型见图1所示。

图1 主体结构模型

3 拉索损伤静力特性影响分析

3.1 荷载工况组合

为研究拉索在最不利损伤组合工况下对桥梁结构的静力特性影响[4-6]，本文将左边跨拉索编号为LS10(A)～LS1 (A)、LS10(B)～LS1 (B)，中跨拉索编号为LS11(A)～LS20 (A)、LS11(B)～LS20 (B)、RS20(A)～RS11 (A)和RS20(B)～RS11 (B)，右边跨拉索编号为RS1(A)～RS10 (A)、RS1(B)～RS10 (B)。以不同位置情况下拉索相同程度损伤(损伤40%)、相同位置情况下拉索不同程度损伤、长中短索对称损伤和非对称损伤几种进行工况组合，共分析24组工况，具体组合见下表2。

表2 斜拉索各损伤组合工况

目前大多斜拉索的主要材料仍以钢绞线构成，拉索损伤也就是部分钢绞线的破断，索力值由剩余钢绞线组成的有效承载面积决定。在有限元建模中可通过降低弹性模量的方式来模拟拉索损伤[7-9]，拉索损伤后的弹性模量E(Ψ)公式如下：

E(Ψ)=(1-Ψ)E

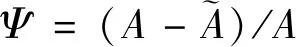
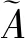
为研究拉索不同程度损伤对桥梁结构静力特性的影响，可将拉索损伤分为：损伤10%、损伤30%、损伤50%、损伤70%、损伤100%五种工况。各工况下拉索损伤后的理论弹性模量取值如下表3。

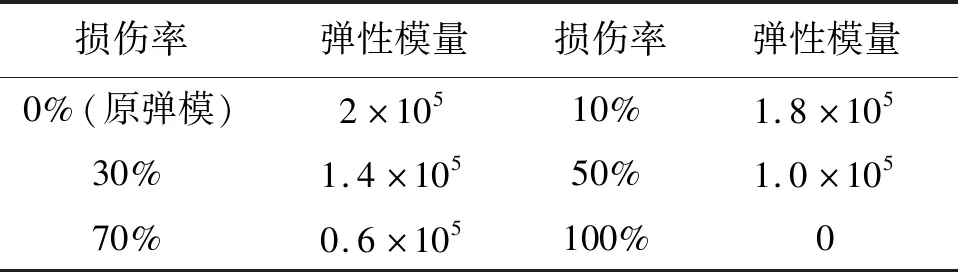
表3 各工况下拉索损伤后的理论弹性模量值(MPa)

3.2 拉索损伤对主梁线形的影响

为研究拉索损伤对斜拉桥主梁线形的影响，从相同损伤程度(损伤40%)下非对称损伤情况、相同损伤程度下对称损伤情况和相同位置下拉索不同程度损伤(非对称)三个方面模拟分析主梁线形的变化规律，如下图2～4所示。

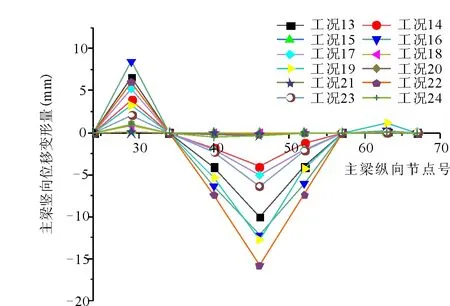
图2 相同损伤程度拉索非对称损伤情况下主梁关键截面位移变化情况

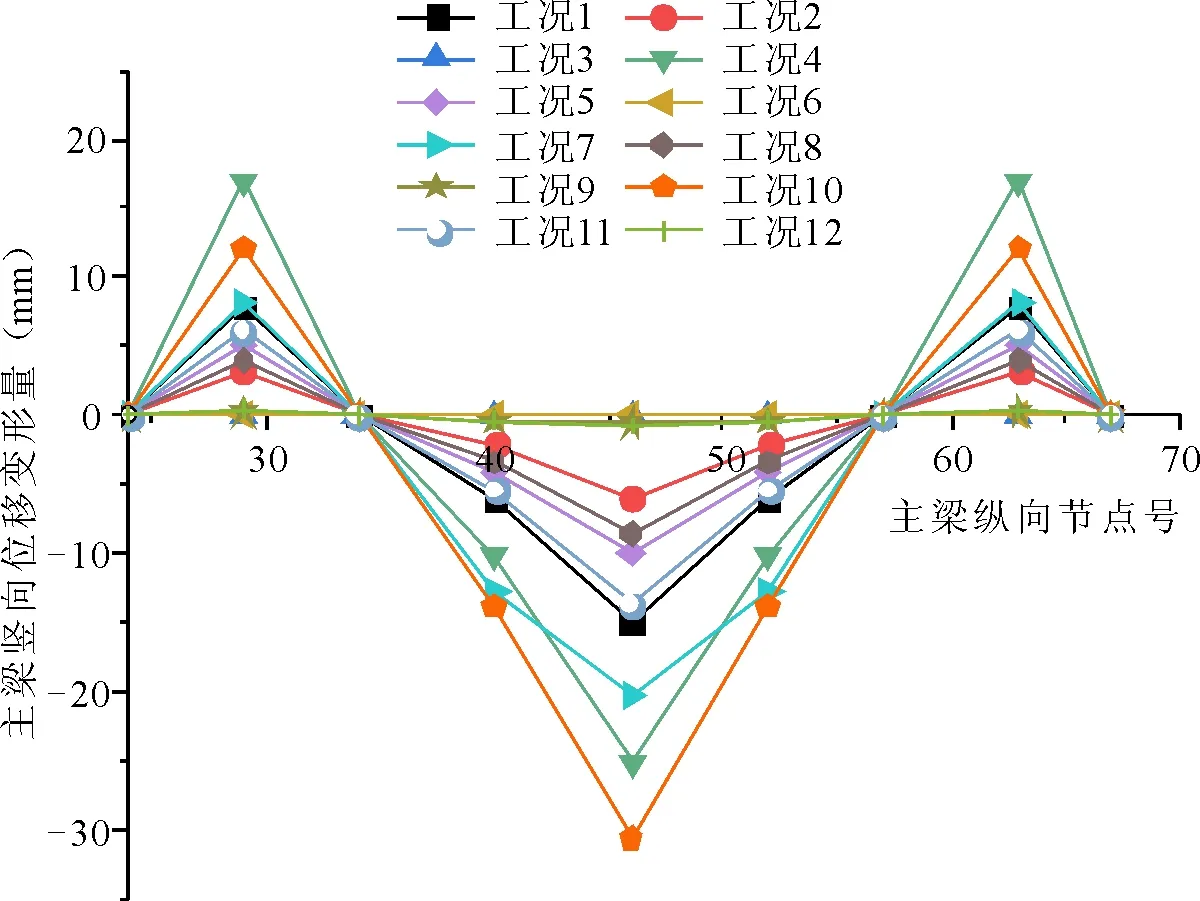
图3 相同损伤程度拉索对称损伤情况下主梁关键截面位移变化情况

图4 相同位置下拉索不同程度损伤对主梁关键截面线形的影响(非对称)

由上图可得出如下结论：

(1)相同损伤情况下不同位置拉索损伤后，边跨长索的损伤对主梁线形影响非常大，使得主跨跨中挠度和边跨跨中反拱度明显增大。边跨中索和短索对主梁线形的影响相对较小，仅在损伤拉索附近有影响；

(2)不对称边跨拉索损伤主要影响本侧桥跨主梁线形，对异侧影响较小(几乎没有影响)，对称边跨拉索损伤和主跨拉索损伤均会对全桥主梁线形有影响；

(3)主塔附近的短索损伤对主梁线形影响最小，主梁线形基本与未损伤时一致；

(4)同一位置损伤情况下，主梁线形变化随着拉索损伤程度的增加而有相似规律性的增大。

3.3 拉索损伤对索力的影响

由主梁线形变化规律可知，最大变形量位于边跨长索处，从相同损伤程度(损伤40%)情况下拉索不同位置损伤和相同位置情况下拉索不同程度损伤(非对称)两个方面模拟分析索力的变化规律，如下图5～6所示。

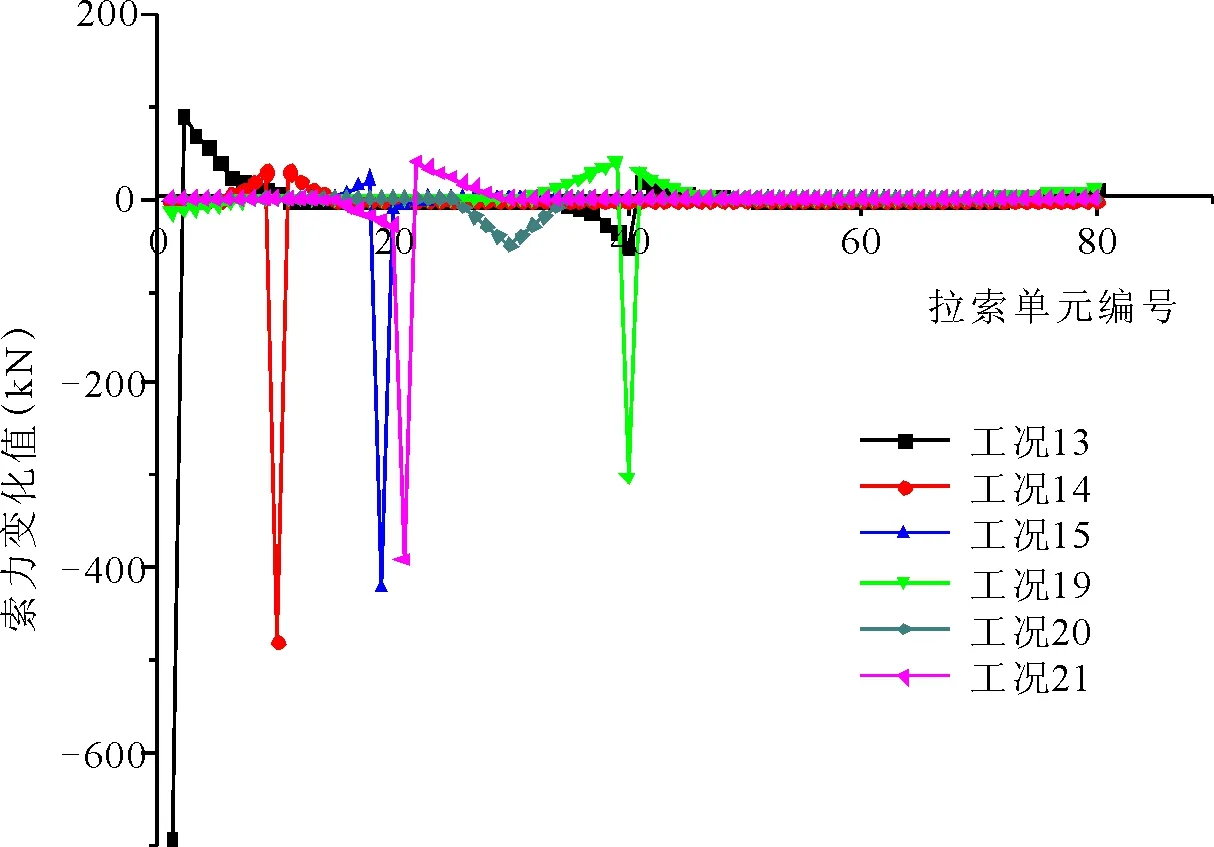
图5 相同程度损伤下拉索不同位置损伤索力变化

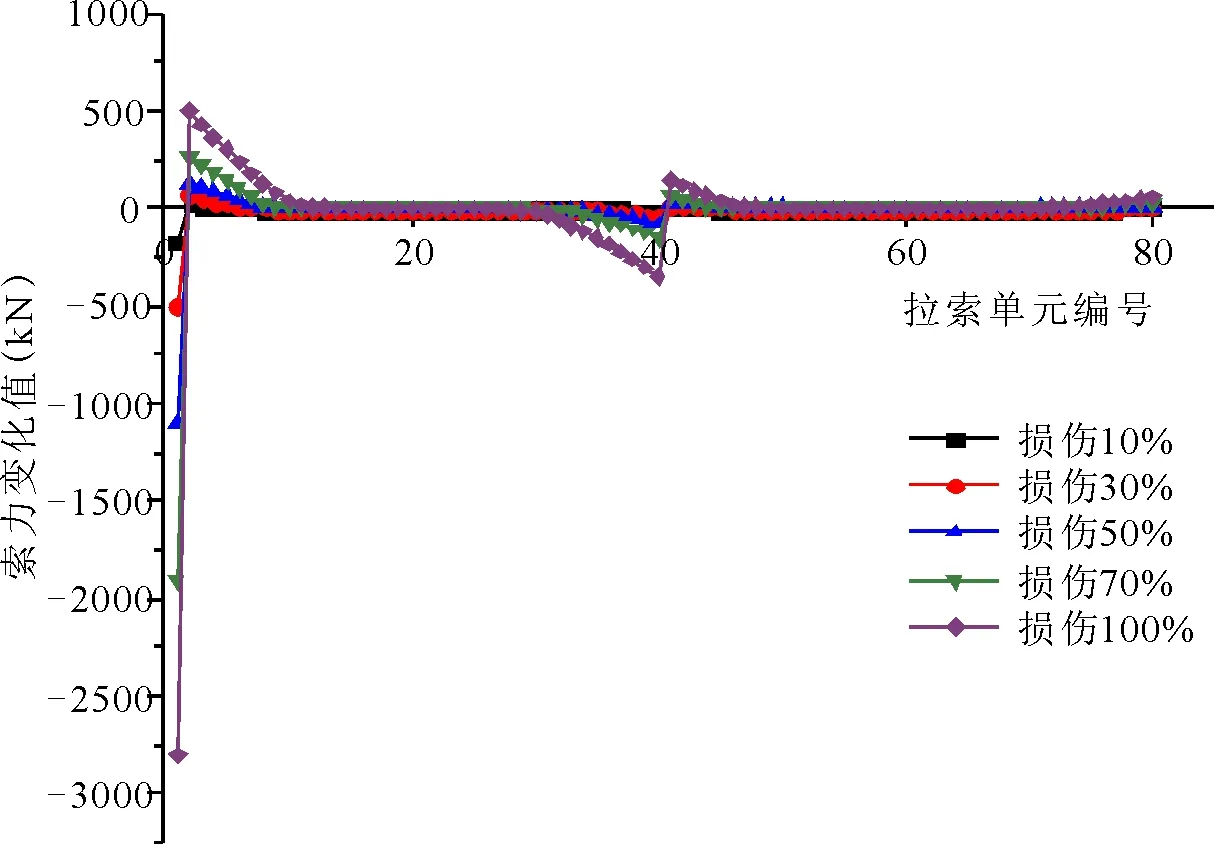
图6 相同位置下拉索不同程度损伤对索力变化

由上图可得出如下结论：

(1)边跨长索的损伤对拉索索力变化影响最明显，损伤后附近拉索索力增加较明显，跨中偏向损伤拉索一侧索力减小，跨中偏离损伤拉索一侧索力增大；

(2)其他中短索损伤对自身附近拉索影响较大，对其他拉索影响较小(几乎没有影响)，单根拉索损伤主要影响同侧拉索索力；

(3)主塔附近的短索损伤后对索力变化值影响相对较小，使其同侧拉索索力值增大，异侧减小；

(4)拉索索力随着自身损伤程度的增大而有相似规律性的减小，损伤同侧拉索索力随着损伤程度的增加而增大，异侧则相反。

4 结 论

通过研究拉索损伤对桥梁线形和拉索索力的影响规律，得出如下结论：

(1)相同程度损伤情况下不同位置拉索损伤后，边跨长索损伤对主梁线形和拉索索力影响最为明显，中短索的损伤对二者的影响相对较小；不对称边跨拉索损伤只对本侧拉索索力及主梁线形有影响，对异侧结构状态基本无影响；

(2)拉索对称损伤时对主梁线形和拉索索力均有影响，在损伤的拉索位置处变化最为明显，主塔附近的短索损伤对二者影响最小；

(3)相同位置情况下拉索不同程度损伤对主梁线形和拉索索力呈规律性影响变化，主梁线形随损伤程度的增加而有相似规律性增大，拉索索力随损伤程度的增加而有相似规律性减小。