基于灰色ARIMA组合模型的砂石骨料物流需求预测——以浙江省为例

卢尔赛，张改平，赵良，张朝晖

（1.交通运输部科学研究院，北京 100029；2.日昌升集团有限公司，浙江 杭州 310002）

0 引言

砂石骨料是一种在混凝土中起骨架、填充和稳定体积作用的岩石颗粒等粒状松散材料，广泛应用于房屋建设、交通基础设施建设、市政工程建设等领域，是我国基础设施建设用量较大且不可或缺的原材料。2021 年，我国砂石骨料产量居大宗物资首位，为200 亿t[1]。为了更好地保障砂石骨料供应、节约砂石骨料资源，应对砂石骨料物流需求进行精准预测。目前国内砂石骨料市场需求预测主要依靠经验，误差较大，已不适应目前经济迅速发展的形势。因此，准确地预测砂石骨料物流需求，对于节约砂石骨料资源、保障砂石骨料供应具有一定的现实意义。

目前，物流需求量预测方法有很多。国外学者对物流需求预测研究起步较早，且集中于改进单一算法的缺陷、提高单一算法的精度方面。Bruzda[2]基于大数据分析研究出一种新型农产品物流需求量预测系统，并设计了系统的软硬件部分；Baisariyev等[3]运用Bootstrap 方法对航空备件物流需求进行了预测；Erwin等[4]运用改进灰色模型对人道主义物流需求进行预测，以进一步优化阿姆斯特丹行动中心的物流调配过程；Ryuichi等[5]通过建立贸易物流预测模型，基于亚太经合组织的贸易额对该组织成员国的国际物流进行了预测。国内学者对物流需求预测的研究思路与国外学者的相似，也着重于研究单一算法精度的提高。陈长英[6]以2008—2017 年的广西壮族自治区货运量为基础，运用改进的灰色-马尔可夫链模型对广西壮族自治区货运周转量进行了预测，得出该自治区物流需求量将逐年递增的结论；王子健[7]运用BP 神经网络对关中平原城市群中不同城市物流需求进行了预测，并根据未来物流需求走向对城市群内部各个城市之间的物流竞争力进行了评价；李明书等[8]基于时间序列法选择ARIMA模型对长春市邮政物流总量进行了研究与预测，结果表明ARIMA模型对呈周期性变化的时间序列预测较为准确，可以用来进行邮政物流总量预测；谭伟华[9]融合多元回归分析法与神经网络分析法，对江西省物流需求进行了预测；王晓平等[10]提出了基于支持向量机模型的北京城镇农产品冷链物流需求预测方法，并验证了新构建模型的预测结果具有较高的精度，可在一定程度上为相关决策提供依据；徐慧[11]构建了基于q阶模糊的层次分析法，对医药应急物流供应能力水平进行评价及预测，并有效解决了已有的模糊层次分析法不足以匹配模糊分析水平的问题；刘庆庆等[12]基于2010—2019 年连云港物流量数据，运用灰色GM(1,1)模型对连云港2020—2024 年物流需求量进行了预测研究，并确定了GM(1,1)模型的精度。

综合来看，以往的研究多基于原始数据直接建模，并往往运用单一的预测方式。如果单纯运用一种模型进行预测，对数据的规律性要求较高，但现实数据往往没有很强的规律性，导致预测结果误差较大。因此，为减小预测结果的误差，有必要运用多模型组合进行预测[5-9]。组合预测是指将广泛认可的预测模型，比如灰色GM(1,1)模型、多元回归模型、马尔科夫链模型、ARIMA模型、BP神经网络模型等组合运用，一般组合方法为先运用GM(1,1)模型或多元回归模型对原始数据进行处理，再用马尔科夫链、ARIMA 模型等进行预测。组合预测在使用无序的时间序列数据前,先对数据进行回归处理，再进行预测，可以在一定程度上提高预测的准确性[6]。

因此，本文运用灰色GM(1,1)模型与ARIMA模型对砂石骨料物流需求进行组合预测。首先运用灰色ARIMA 模型和GM(1,1)模型对浙江省水泥产量进行预测，然后以真实产量为基准进行对比研究，验证灰色ARIMA 模型的预测精度。接下来运用灰色ARIMA 模型对浙江省2021—2025年的砂石骨料需求量进行预测。

1 模型构建

1.1 问题描述

砂石骨料物流需求的增长水平受经济环境、人口规模、建设政策等可知因素以及突发重大事件、突发政策、自然灾害等无法预测的未知因素的影响，且相互之间关系复杂、变化无序、相互影响，难以做到客观量化，是一个典型的灰色系统，故可用灰色GM(1,1)模型进行预测。但灰色预测依然存在一定的问题，即对时间序列的平滑性要求较高，如果平滑性不够高，则会产生较大误差。为此，本文在对原始时间序列进行灰色处理后，运用ARIMA模型对时间序列数据进行预测，以降低数据平滑性不足带来的误差。

1.2 灰色ARIMA组合模型

灰色ARIMA 组合模型主要由灰色预测模型和ARIMA 模型组合而成。首先建立灰色预测模型对产量数据序列进行拟合，然后建立ARIMA模型对灰色模型的拟合误差序列进行预测[13-14]，最后将两种模型的预测值求和构成产量预测值。

组合模型的预测步骤如下：

（1）设训练集X(0)={X(0)(1),X(0)(2),…,X(0)(n)}，并设预测数据长度为r的观测数据集为X(0)′={X(0)(n+1),X(0)(n+2),…,X(0)(n+r)}。对训练集序列建立灰色GM(1,1)预测模型，得拟合序列(0)(n)，并用残差检验法对灰色预测结果进行检验[15-17]。

（4）对差分处理后的平稳序列建立ARIMA模型，运用自相关分析法对序列的自相关和偏相关函数图进行模型阶数初步识别，参照表1，经过AIC 准则判定，针对ARIMA（p,d,q）（p 为自回归项系数，q为滑动平均项数，d 为使数列成为平稳序列所进行的差分次数）模型确定结果最优时对应的p,q，并用该模型得到误差预测序列

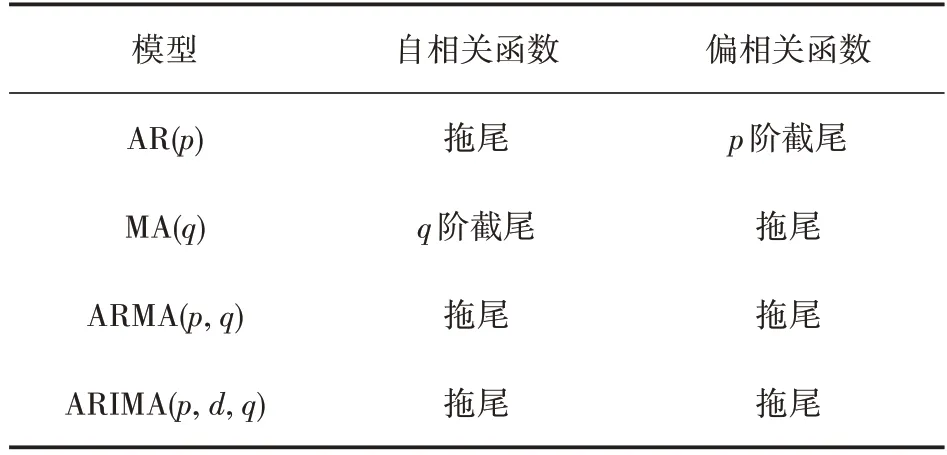
表1 ARIMA模型的相关性特征

（6）对ARIMA 模型拟合结果进行白噪声检验，若未通过检验，说明还有一些重要的信息没有提取，则回到步骤（5）对拟合模型进行重新设定，直到通过白噪声检验。

灰色ARIMA模型的预测流程如图1所示。

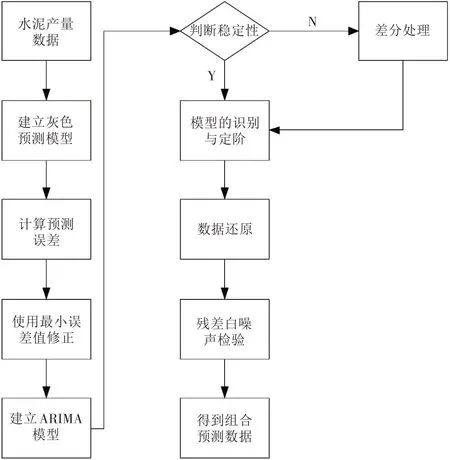
图1 灰色ARIMA模型的预测流程

2 实证分析

2.1 浙江省砂石骨料物流需求现状

由于砂石骨料需求市场没有官方统计，市场不规范，且国家规定的开采量与实际开采量之间差异较大，故本文首先梳理砂石骨料供需情况，以得到砂石骨料需求总量的实际构成。2021 年，中国200亿t的砂石骨料需求量总体自给自足，进出口总量在3 000 万t 以下[24]，故在计算砂石骨料总需求时，不需要考虑进出口量。根据《2021 年中国砂石行业运行报告》，砂石需求、运输和供给如图2所示[24]。

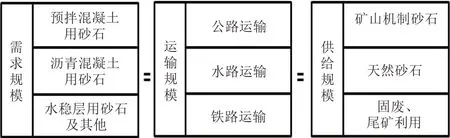
图2 砂石骨料供需关系图

从图2 中可以看出，砂石骨料的总需求规模D为预拌混凝土用砂石需求量、沥青混凝土用砂石需求量和水稳层用砂石需求量的总和，即：

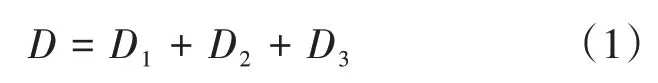
式（1）中：D为砂石骨料总需求量；D1为预拌混凝土用砂石需求量；D2为沥青混凝土用砂石需求量；D3为水稳层用砂石需求量。

预拌混凝土用砂石量D1可通过各地水泥产量推测。水泥砂石配比往往按照水泥∶砂石骨料=1∶6 来进行混合，即水泥用量是砂石骨料用量的1/6。同时，根据《2021 年中国砂石行业运行报告》得出，D1约占市场总需求量的70%[24]。基于上述条件，可根据水泥产量近似推算砂石骨料需求量D：

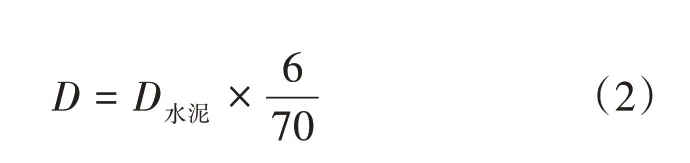
式（2）中：D水泥为水泥产量。

2.2 模型精度验证及求解

根据上述分析，本文选择1990—2020年浙江省水泥产量（资料来源于1990—2020年的《浙江省统计年鉴》[25]）来预估浙江省2021—2025 年砂石骨料需求，建立灰色ARIMA组合模型进行拟合和预测。

首先，基于1990—2015 年的水泥产量数据（见图3），分别运用GM(1,1)模型与灰色ARIMA模型预测2016—2020年水泥产量数据，并将预测结果与真实产量进行对比，以验证灰色ARIMA模型的预测精度。

图3 浙江省1991—2015年水泥产量

然后对浙江省2021—2025年的水泥产量进行预测，最后根据水泥产量预测值对该省相应年份的砂石骨料需求量进行预测，以得出浙江省2021—2025年的砂石骨料物流需求量。

由图3 可看出，水泥生产量出现了几个特殊的节点：在1990—1998年，水泥生产量保持平缓上升趋势；在1999—2008年间水泥生产量快速上升；自2009年之后，产量在波动中呈缓慢上升趋势，且伴随下降趋势。

运用GM(1,1)模型对1990—2015 年的水泥产量数据进行拟合，分析并预测2016—2020年的水泥生产量。GM(1,1)模型预测值如表2所示。

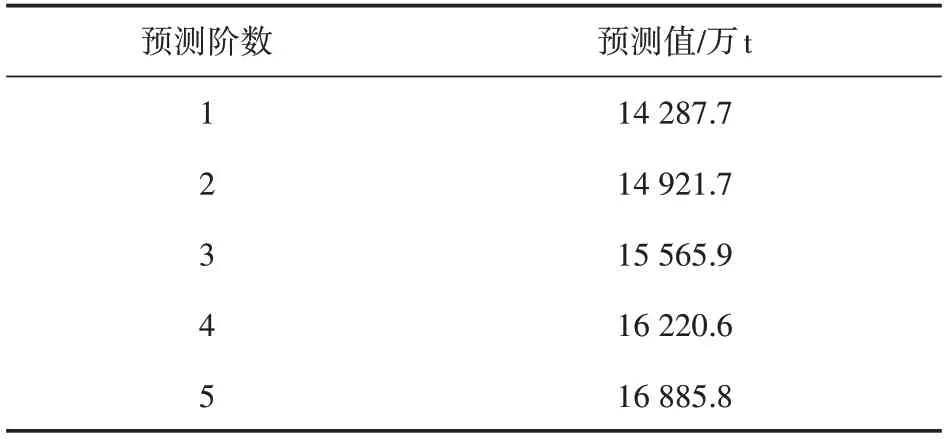
表2 GM(1,1)模型预测值

GM(1,1)模型预测拟合结果如图4所示。

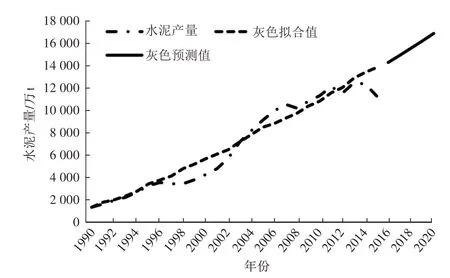
图4 浙江省水泥产量GM（1,1）模型结果拟合图

从拟合曲线以及预测值上看，单一的GM(1,1)模型预测误差较大，需要应用更高精度的预测模型才能更好地对浙江省水泥产量进行预测。

对水泥生产量实际值和GM(1,1)模型拟合值求残差序列，再将非负处理后的灰色残差序列代入ARIMA 模型进行ADF 平稳性检验，检验结果如表3所示。

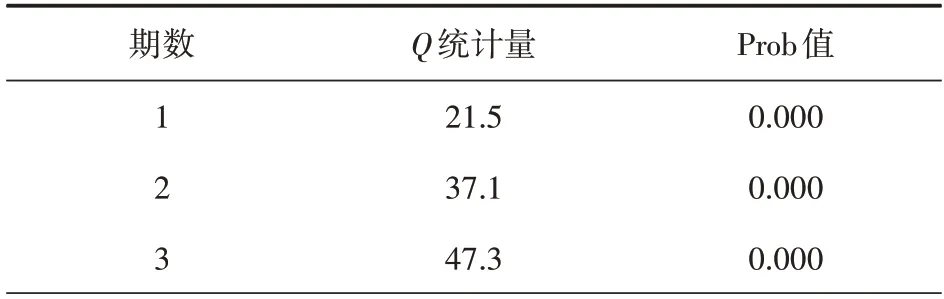
表3 ADF平稳性检验结果

表3 （续）

要判断序列是否平稳，需要看ADF 检验结果中的Prob 值，当大多数的Prob 值都大于0.05（置信水平）时序列为白噪声序列，序列平稳；反之则为非平稳序列。由表3 中Prob 值可知序列是非平稳的，需要对序列进行差分处理。

对序列进行一阶差分处理，即d=1，结果如表4 所示。由于此时Prob 值全部大于0.05，所以序列是平稳的，停止差分处理，对其进行相关性检验，结果如表5所示。

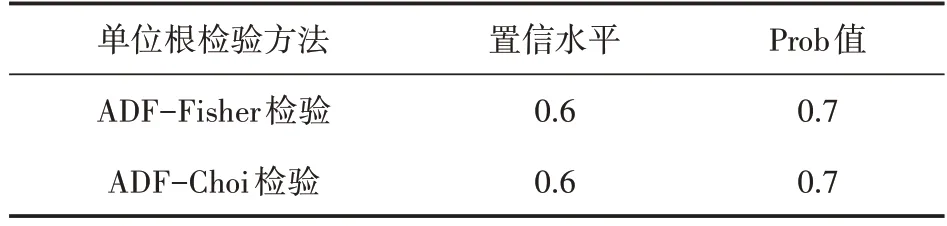
表4 ADF单位根检验

表5 残差序列的自相关和偏相关函数

由于此时Prob 值全部大于0.05，所以序列是平稳的，此时停止差分处理，对其相关性进行检验。通过表5 可初步判断，自相关函数拖尾，偏相关函数拖尾，并且其中p与q的AIC值在p=3,q=4时达到最小，即选定最优模型为ARIMA(3,1,4)。

模型阶数确定后，运用ARIMA(3,1,4)模型对GM(1,1)模型的残差修正值进行拟合，然后将ARIMA 预测模型差分还原后的数据与GM(1,1)模型预测数据相加，即为灰色ARIMA 组合模型对于2021—2025 年浙江省水泥产量的最终预测结果，如图5所示。

图5 浙江省水泥产量组合模型结果拟合图

从图5 可以看出，灰色ARIMA 组合模型的拟合精度明显优于GM(1,1)模型。两种模型的预测值如表6所示。

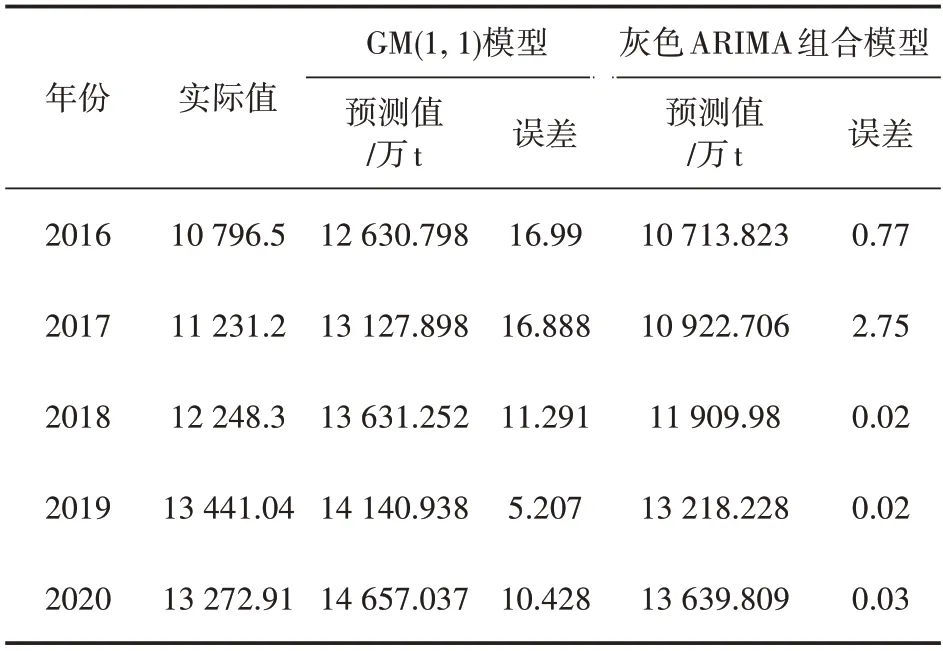
表6 GM(1,1)模型和灰色ARIMA组合模型预测值

由表6 可知，灰色ARIMA 组合模型的预测精度较高，可用于预测浙江省2021—2025年的水泥产量，预测结果如表7所示。

表7 2021—2025年浙江省水泥产量预测值

将上述数据代入式（2）计算可得，浙江省2021—2025的砂石骨料物流需求量，如表8所示。

表8 浙江省2021—2025的砂石骨料物流需求预测值

3 结语

本文采用灰色ARIMA组合模型对浙江省砂石骨料物流需求量进行了预测研究。通过对比GM(1,1)模型与灰色ARIMA 组合模型预测结果，验证了灰色ARIMA 组合模型相较于GM(1,1)有更高的精度，确认了灰色ARIMA模型的实用性。运用灰色ARIMA组合模型对浙江省砂石骨料需求进行预测，结果显示2021—2025年浙江省的砂石骨料需求量会继续呈现不断上升的趋势。但本文在研究中未考虑到砂石骨料物流需求量的精准求法，下一步的研究方向是运用大数据算法对砂石骨料的用量进行精确求解，以更好地对砂石骨料需求量进行预测。