基坑上跨开挖诱发既有盾构隧道隆起变形研究
2022-11-30王理想梁荣柱李忠超肖铭钊吴文兵
王理想,梁荣柱,李忠超,康 成,肖铭钊,吴文兵,高 坤,郭 杨
(1. 中国地质大学(武汉)工程学院,湖北,武汉 430074;2. 武汉市市政建设集团有限公司,湖北,武汉 430023;3. 安徽省建筑科学研究设计院,安徽,合肥 230031;4. 绿色建筑与装配式建造安徽省重点实验室,安徽,合肥 230031)
盾构隧道是由众多管片拼接而成的细长结构体,是目前地铁隧道结构的主要形式之一。随着地铁线路网状化建设发展,隧道结构不可避免地遭受沿线建筑施工的影响,商业建筑和市政设施上跨地铁线路开挖施工已经成为常态,这给地铁隧道结构保护带来了新的挑战[1]。以建筑基坑上跨开挖为例。图1 为上跨基坑开挖卸载对下卧盾构隧道影响示意图。基坑开挖卸载将会引起地层的应力释放,诱发隧道纵向不均匀位移,严重者将会造成隧道管片破裂、接头张开、防水失效等一系列问题,严重威胁地铁列车的运行安全。因此,预测和评估基坑上跨开挖诱发紧邻地铁隧道的变形和受力影响是目前城市轨道建设中较为紧迫的问题之一。
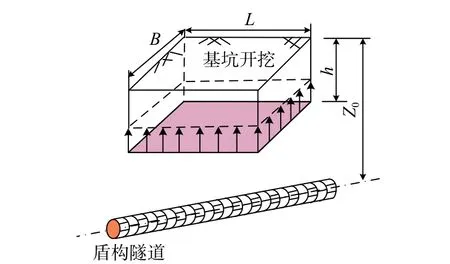
图1 上跨基坑开挖对既有盾构隧道影响示意图Fig. 1 Impacts of over-crossing excavation on existing shield tunnel
目前在预测盾构隧道在上跨基坑开挖下的变形和受力响应方面,国内外学者分别提出了不同的理论解析方法。张治国等[2]简化盾构隧道为搁置于Winkler 地基上的Euler-Bernoulli 梁,用两阶段分析法求解盾构隧道变形和受力。黄栩等[3]则考虑到Winkler 地基模型不连续的缺点,引入三参数Kerr 弹性地基模型取代Winkler 地基,而盾构隧道同样简化为Euler-Bernoulli 梁,推导得到基坑上跨卸载条件下盾构隧道的纵向变形。LIANG 等[4]则采用Pasternak 地基模型考虑土体与隧道的相互作用,仍将隧道视为Euler-Bernoulli 长梁,通过差分法获得盾构隧道的纵向变形。随后,梁荣柱等[5−6]指出Euler-Bernoulli 梁实际上假定梁的剪切刚度无穷大,无法反映盾构隧道环间接头对整体刚度的弱化,建议简化盾构隧道为可考虑接头弱化的Timoshenko 梁模型,分别结合Winkler 地基模型和Pasternak 地基模型求解基坑开挖引起的邻近地铁隧道的竖向位移、内力、张开量和错台量。在此基础上,LIU 等[7]简化盾构隧道为Timoshenko梁,通过Vlazov 地基考虑隧道与地基相互作用,建立基坑开挖引起的盾构隧道纵向变形解析解。
总结前人的理论方法,可以发现前述方法均是将盾构隧道简化为有限长度的连续梁(如Euler-Bernoulli 梁或Timoshenko 梁模型),通过弹性地基考虑隧道与地层的相互作用。然而盾构隧道是由管片和螺栓拼接而成的,管片和接头的力学性能差别较大[8],环间接头为盾构隧道的薄弱环节[9−10]。因此,无论是Euler-Bernoulli 梁模型还是Timoshenko 梁模型均是假定盾构隧道为连续结构,无法有效考虑接头对隧道纵向变形的影响。
针对连续梁模型的缺点,为进一步反映盾构隧道的真实受力变形特点,周顺华等[11]将盾构隧道视为由剪切弹簧连接而成的一系列弹性短梁,认为盾构隧道的变形全部由剪切错台构成,并利用最小势能原理求解基坑开挖引起的隧道变形,但该方法没有考虑盾构隧道的环间转动的影响。魏新江等[12]在研究地面堆载对盾构隧道的影响时提出一种能够同时考虑隧道管片环转动和错台的模型,魏纲等[13]将该模型应用于基坑开挖引起的隧道变形研究中,但该模型计算环间转动的方法仍有待进一步完善。
此外,现有理论通常使用Winker 地基、Pasternak 地基、Vlazov 地基或者Kerr 地基等弹性地基模型来模拟地基土与隧道的相互作用,然而地基土并非弹性体。在地基土变形过程中,其呈现明显的非线性特征,故而使用弹性地基模型也无法有效模拟真实情况。
本文引入非线性Pasternak 地基模型[14]考虑地基的非线性变形特征,构建带环间接头盾构隧道计算模型反映环间接头的弱化作用。通过两阶段分析法建立基坑上跨作用下盾构隧道纵向位移和张开量简化解答:首先,通过MINDLIN 解求解基坑开挖产生的作用于下卧盾构隧道上的附加荷载;其次,建立基坑卸载下盾构隧道纵向变形微分方程,利用有限差分法求解隧道纵向变形和内力。最后与三个基坑上跨既有盾构隧道的工程实测数据及前人理论方法对比,以验证所提预测方法的适用性。
1 上跨基坑卸载下既有盾构隧道纵向变形理论推导
1.1 基本假定
图2 为基坑卸载下盾构隧道受卸荷作用示意图。上跨基坑开挖引起地层卸荷,卸荷应力作用于下卧盾构隧道造成其隆起位移和管片张开。本文主要考虑竖向卸荷引起盾构隧道纵向变形,主要假定如下:① 仅考虑基坑开挖引起的竖向卸载,不考虑基坑侧壁的卸载效应。② 盾构隧道与土层始终紧密接触,不考虑盾构隧道与土层脱开;③ 不考虑开挖的时间效应和软土固结效应的影响。

图2 基坑上跨施工下基坑-盾构隧道相互作用计算模型Fig. 2 Excavation-shield tunnel interaction calculation model due to over-crossing excavation
为简化计算,通过两阶段分析法推导基坑上跨开挖引起的下卧盾构隧道纵向隆起变形:首先,通过MINDLIN 经典解求得基坑卸载下作用于隧道的附加卸荷荷载p(x);其次,构建盾构隧道环间接头模型,施加附加卸荷荷载p(x)于盾构隧道,构建其纵向变形微分方程,通过有限差分法求解,并进一步获得接头张开量分布。
1.2 基坑开挖引起邻近隧道附加荷载计算
图3 为基坑与盾构隧道平面相对位置图。考虑到目前大多数基坑为矩形或四边形,因此,本文主要针对矩形基坑,L为基坑长,B为宽,d为两个坐标系原点的距离,α 为x轴与ζ 轴的夹角,β 为两坐标系原点连线与ζ 轴的夹角。对于其他异型基坑形状,可分割为多个矩形,通过叠加求解基坑卸荷。利用MINDLIN[15]解估算基坑开挖引起的作用于既有隧道上的附加荷载p(x):

图3 基坑与既有隧道相对位置平面示意图Fig. 3 Plane diagram of relative position between excavation and existing tunnel

式中:z0为既有盾构隧道轴线埋深;h为基坑开挖深度;ν为土层泊松比;γi为基坑开挖第i层土的重度;Hi为第i层土的厚度;n为基坑开挖土层的数量;参数R1、R2分别为:


1.3 地基模型及隧道模型
1.3.1 非线性Pasternak 地基模型
LIANG[14]指出目前的大多数弹性地基模型如Winkler、Pasternak 或Kerr 地基均是考虑长梁发生沉降变形时长梁与地基的相互作用,通过实验获得其地基反力参数,此时长梁相对土体向下运动;而对于卸载工况下如基坑卸荷和新建隧道上穿,盾构隧道发生隆起变形,此时盾构隧道相对于土体向上运动。因此,Winkler、Pasternak 或Kerr地基并不适用于考虑长梁或盾构隧道隆起变形的工况。针对既有地基模型的不足,LIANG[14]提出了适用于计算黏土地层中上部卸荷引起的既有盾构隧道隆起变形的非线性Pasternak 地基模型:
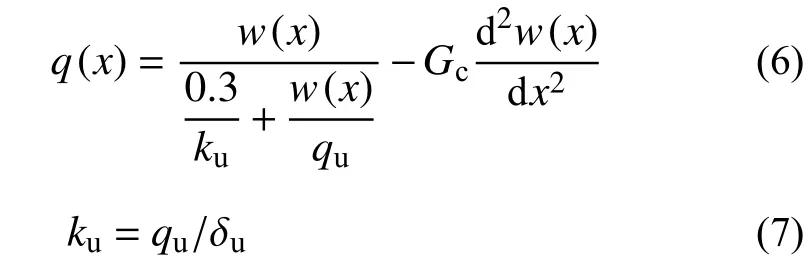
式中:q(x)为地基反力;w(x)为地基土变形量;qu为极限地层反力,qu=SuNcv,Su为地基土不排水抗剪强度(取土层弹性模量的1/350[16]),Ncv为竖向隆起系数; δu为获得极限地层反力所需要的地基土变形值,对于黏性土一般取0.01 倍~0.015 倍的隧道埋深z0;Gc为地基土剪切层刚度。竖向隆起系数Ncv和地基土剪切刚度Gc分别通过以下两式确定:

式中:Es为土层的弹性模量;Ht为剪切层厚度,一般取2.5 倍隧道直径[17];D为隧道直径。
1.3.2 带环间接头盾构隧道计算模型
一般地铁盾构隧道通常由6 片管片拼装成1 环,管片环之间相互连接形成盾构隧道整体。可见,管片环间接头的存在是盾构隧道区别于一般连续细长结构物(如超长桩、连续管道等)的明显特征,这导致盾构隧道受力变形与连续细长结构物有所不同。比如,在受荷变形时,盾构隧道环间接头发生张开,以及弯矩在环间接头处出现不连续等。因此,采用连续长梁如Euler-Bernoulli 梁和Timoshenko 梁模拟盾构隧道的受力变形,不能反映盾构隧道环间接头的受力和变形特征。环间接头往往是盾构隧道结构的薄弱点,渗漏水、衬砌破损均发生在环间接头部位。因此,必须充分考虑到环间接头存在对盾构隧道变形的影响。
为考虑环间接头存在的影响,把盾构隧道划分管片环和环间接头,通过两者的组合形成完整的盾构隧道结构。图4 为带环间接头盾构隧道简化示意图。盾构隧道管片环视为Euler-Bernoulli 短梁,称之为标准环单元,其长度为管片环宽度;将环间接头部分视为无长度的转动弹簧,称之为接头单元。下文分别从标准环单元和环间接头单元出发,构建其受力变形微分方程并进行有限差分求解。
取图4 中盾构隧道任意标准环进行微分单元的受力分析,并结合Euler 梁原理,可以得到非线性 Pasternak 地基上标准环单元的纵向变形微分方程:
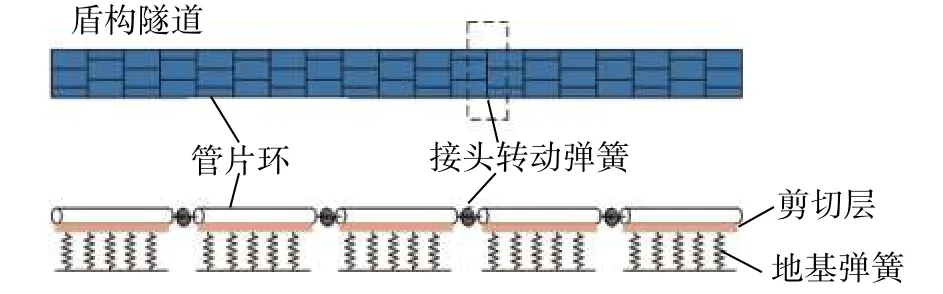
图4 带环间接头盾构隧道简化示意图Fig. 4 Schematic diagram of calculation model of joint discontinuous shield tunnel

式(10)为四阶非齐次微分方程,可利用有限差分法求其数值解。图5 为盾构隧道离散示意图。假设盾构隧道有ns个管片环,每个管片环离散为nt个单元,则隧道总计被离散为n−1(n−1=nt×ns)个单元,即n个节点,每个单元长度l=ls/nt,ls为管片环长度。为考虑隧道边界条件,分别在隧道两端各增设2 个虚拟节点,总计有n+4 个节点。假设其中有m个节点位于隧道环间接头位置,则除去环间接头及其相邻节点有n−3m个节点属于标准环单元。

图5 盾构隧道有限差分离散示意图Fig. 5 Discretization of shield tunnel for finite difference
1.4 标准环单元推导及有限差分求解
根据有限差分原理,可得到式(10)有限差分表达式为:
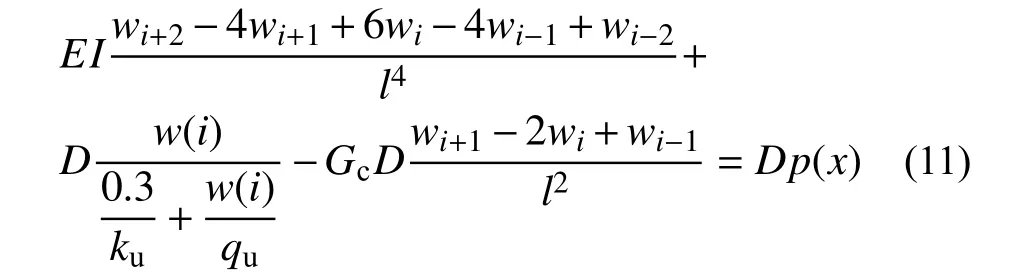
式 中:wi+2、wi+1、wi、wi−1和wi−2为 节 点i+2、i+1、i、i−1 和i−2 的竖向位移,以此类推。
式(11)可以得到n−3m个方程,而未知变量一共有n−3m+4 个。需通过盾构隧道边界条件获得另外4 个变量的表达式,即可满足求解条件。
将盾构隧道两端视为自由端,即隧道两端弯矩M和剪力Q均为0,则有:

由中心标准有限差分原理,可得到式(12)的差分表达式:

由式(13)可得到盾构隧道两端4 个虚拟节点w−2、w−1、wn、wn+1的位移表达式:将式(14)代入式(11),可得到盾构隧道标准环单元竖向变形的代数方程表达式。

1.5 接头单元有限差分求解


根据有限差分原理可得接头处弯矩Mj的差分表达式为:


联立式(19)、式(24)~式(26)有:

将式(22)~式(23)代入式(30)和式(31),可得2m个与环间接头相邻的节点的代数方程:

1.6 盾构隧道纵向变形方程的矩阵表达式
结合式(11)、式(29)、式(32)和式(33)便可得到盾构隧道全部n个节点的位移差分方程,可进一步表示为矩阵的形式:

式中:w为隧道竖向位移w(x)的列向量;Kt为既有隧道刚度矩阵;Ks为雅可比矩阵;Gs为剪切层矩阵;P为施加于隧道的附加卸荷p(x)列向量。
由于式(34)为非线性方程组,可使用牛顿迭代法求解,求解过程可参考文献[14]。
已知外部应力p(x)时,由式(34)可得盾构隧道的竖向位移,进而的可以得到既有盾构隧道的弯矩。
将式(22)、式(23)的虚拟节点位移代入式(18)中可以得到在环间接头处的弯矩的m个代数方程:

式中,Mt为系数矩阵。
假定环缝接缝邻近微元为刚体,由图6 可知,盾构隧道纵向环间张开角φ即接头处的相对转动角θ,则:

图6 隧道环间接头增设虚拟节点示意图Fig. 6 Schematic diagram of adding virtual node in tunnel ring joint

2 计算参数的确定
由于本文将盾构隧道管片环简化为Euler 短梁,故需要得到管片环的纵向等效抗弯刚度,并引入折减系数以考虑管片环向接头对管片环刚度的削弱:

式中:β 为盾构隧道管片环纵向抗弯刚度折减系数;Ec为盾构隧道管片弹性模量;t为隧道管片厚度。
对于管片环间接头转动刚度,志波由纪夫等[18]提出了纵向等效抗弯刚度的计算方法,其计算模型如图7 所示。结合志波由纪夫的盾构隧道纵向等效连续模型给出环间接头转动刚度的计算公式:

式中:ls为环宽;I为盾构隧道截面惯性矩;ψ 为表示纵向等效连续模型中的中性轴位置的参数,公式为:

式中:kb为接头螺栓的平均线刚度,kb=EbAb/lb,lb为螺栓长度,Eb为螺栓弹性模量,Ab为螺栓截面面积;Ac为管片环截面积;n为螺栓数。
假设盾构隧道环间接头附近微元体为刚体,由图7 可得到,隧道环间接头张开量Δ的计算公式为:
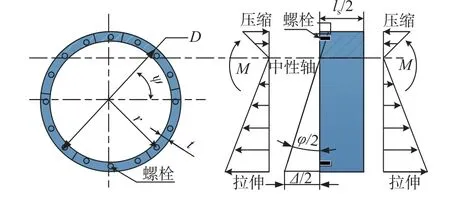
图7 张开量计算示意图Fig. 7 Schematic diagram of opening calculation

式中,r为接头螺栓中心到盾构隧道轴线的距离。
3 实例验证
3.1 杭州延安路某基坑上跨杭州地铁1 号线
杭州延安路某基坑为一矩形基坑,东西长14.83 m,南北宽11.8 m,开挖深度为8.2 m。杭州地铁1 号线左线由基坑正下方穿过,隧道埋深为15.2 m,隧道外径为6.2 m,衬砌厚度为0.35 m,管片环宽度为1.2 m,管片环间由16 根M30 高强度螺栓连接[19−21]。孙廉威等指出,杭州地铁1 号线管片环纵向抗弯刚度折减系数取0.7[22],可得管片环纵向抗弯刚度为6.7×108kN·m2,环间接头转动刚度为4.17×107kN·m/rad。本工程为保证基坑下方盾构隧道的安全,对坑底2.9 m 厚的土体使用水泥土搅拌桩进行加固,并在隧道两侧分别设置了抗拔桩。魏纲等[23]指出该基坑工程黏土弹性模量Esc为20 MPa,加固土Esr为200 MPa。本文取加权平均值,土体Es1取71.68 MPa,ν取0.35。本案例获得极限地层反力所需要的地基土变形值δu取0.1976 m,地基土不排水抗剪强度取204.8 kPa,竖向隆起系数Ncv取4.9。
图8 为本文预测结果、协同变形模型[24]计算结果与实测数据的对比曲线图。文献[24]的协同变形模型将盾构隧道视为一系列Euler-Bernoulli 短梁,短梁之间由剪切弹簧和拉伸弹簧连接。由图8 可见,相较于协同变形模型[24]的方法,本文方法计算得到的隧道最大隆起位移稍稍大于实测值,可能所提方法忽略了抗拔桩对地层卸荷的限制,但总体上本文方法计算的隧道隆起变形与实测数据保持一致。由于本文方法充分考虑到环间接头的存在对盾构隧道的弱化作用,故而计算得到的隧道隆起曲线并非光滑曲线,而是在环间接头处出现转折。这说明带环间接头盾构隧道计算模型可以很好地描述盾构隧道的非连续变形特点。
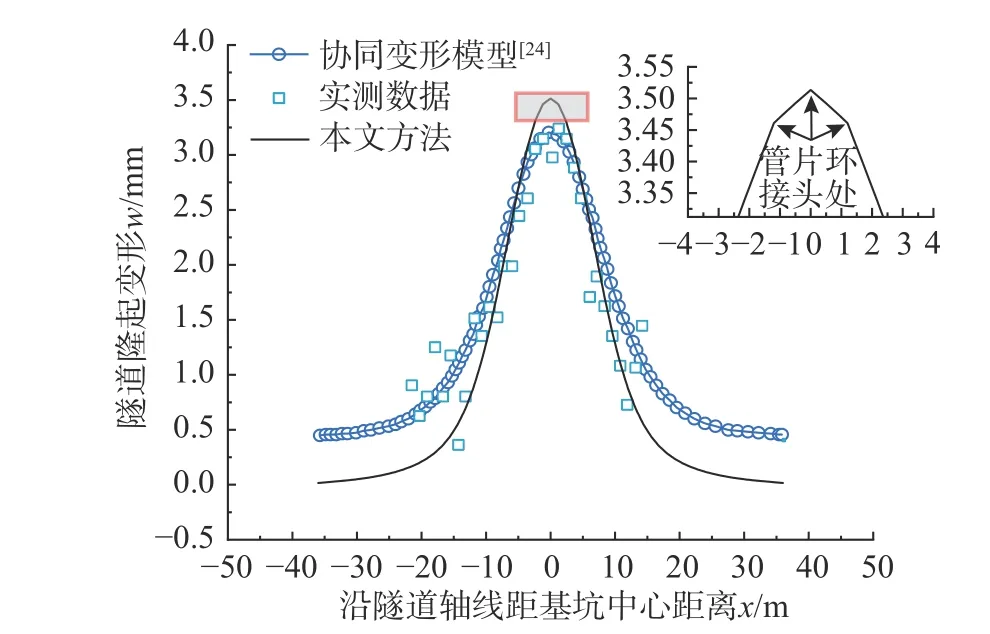
图8 杭州地铁一号线计算结果与实测数据对比Fig. 8 Comparison of calculation results and measured data of Hangzhou Metro Line 1
图9 为计算得到的隧道弯矩分布图。由于盾构隧道是由管片和螺栓拼接而成,并不是均匀连续的整体,所以其受力也是非连续的。由图9 可以看出,所提方法计算得到的弯矩分布曲线在管片环接头处曲线出现转折,这充分说明本文方法可以很好地反映环间接头对盾构隧道受力的影响。
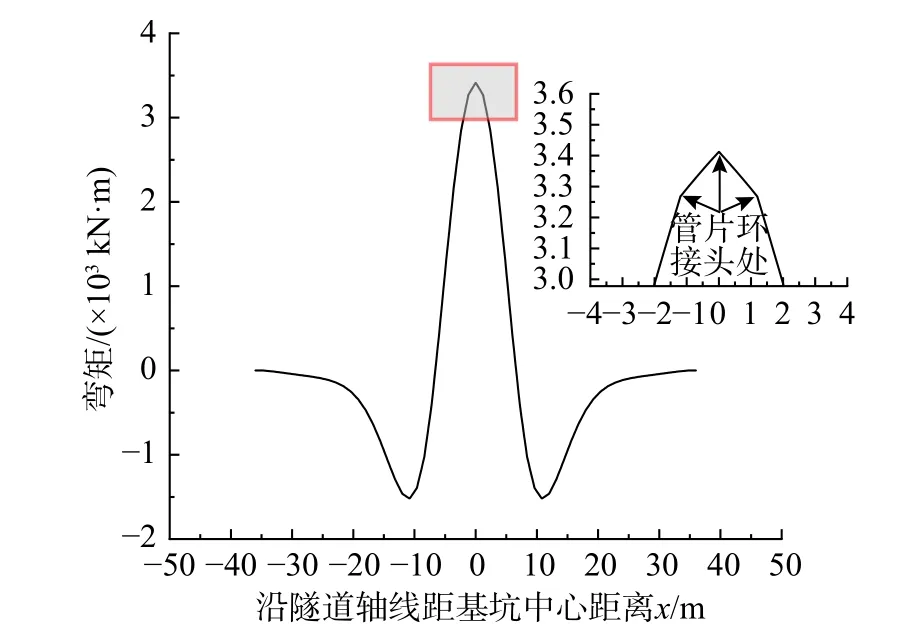
图9 杭州地铁一号线弯矩值Fig. 9 Bending moment value of Hangzhou Metro Line 1
图10 为本文方法隧道环间接头张开量分布图。由图10 可见,计算得到的环间接头张开量分布形态为“w”,在基坑中心处隧道接头张开量最大,在基坑边界处出现负值,整体分布形态受到弯矩分布的控制。可见,由在基坑中部管片张开量最大,因此,这部分盾构隧道管片容易引发渗漏水等问题。
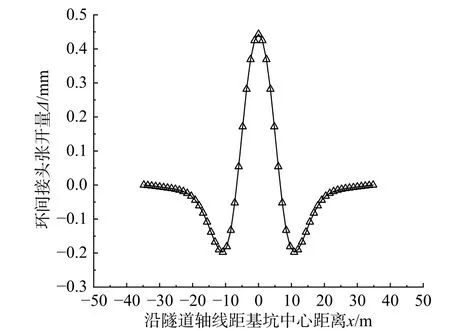
图10 杭州地铁一号线环间接头张开量计算值Fig. 10 Calculation value of joint opening between rings of Hangzhou Metro Line 1
3.2 上海闸北基坑紧邻上海地铁1 号线
上海闸北基坑近似为矩形基坑,基坑长240 m宽230 m,开挖深度为6.45 m[25],属于典型的宽大基坑。上海地铁1 号线于基坑东侧平行通过,隧道轴线距离基坑开挖边线仅8.55 m,隧道轴线埋深为14.9 m,盾构隧道具体参数见文献[6]。隧道埋置于淤泥质粘土中,地基土弹性模量Es2取12 MPa,ν为0.4。隧道管片环纵向抗弯刚度为6.7×108kN·m2,环间接头纵向转动刚度为6.5×107kN·m/rad。本案例获得极限地层反力所需要的地基土变形值δu取0.1863 m,地基土不排水抗剪强度取34.29 kPa,竖向隆起系数Ncv取4.8。
图11 为本文方法预测结果、文献[6]方法计算结果与实测值对比图。文献[6]将盾构隧道简化为Timoshenko 梁,使用线性Pasternak 地基考虑地基与隧道的相互作用。由图11 可以看出,相较于Pasternak 地基-Timoshenko 梁的方法[6],本文方法计算得到的隧道隆起值更加接近实测数据。

图11 上海地铁1 号线隆起值计算结果与实测数据对比Fig. 11 Comparison between calculated and measured uplift values of Shanghai Metro Line 1
图12 和图13 为不同方法计算得到的隧道弯矩和接头张开量对比图。由图可知,Pasternak 地基-Timoshenko 梁的方法[6]方法计算得到的弯矩和接头张开量要明显小于本文方法得到的值,这主要是由于文献[6]将盾构隧道视为连续的Timoshenko梁高估了隧道的整体性所致。而带环间接头盾构隧道计算模型,充分考虑了接头单元和标准环单元在抗弯刚度上的差异,这种差异将产生应力集中,故而计算得到的弯矩与张开量比连续梁模型更大。由于本案例基坑规模较大,长宽均超过200 m,故而基坑内部一定范围内的盾构隧道隆起变形值基本相同,这也导致该范围内的隧道环间接头张开量接近为零。而在基坑边缘附近,隧道隆起变形急剧减小,故而隧道环间接头张开量也快速增大而后迅速减小。图13 显示的结果表明,宽大基坑边缘下方的盾构隧道最易发生破坏,在实际工程中应当对此部位的盾构隧道加强保护。

图12 上海地铁1 号线弯矩值Fig. 12 Bending moment value of Shanghai Metro Line 1

图13 上海地铁1 号线环间接头张开量计算值Fig. 13 Calculation value of joint opening between rings of Shanghai Metro Line 1
3.3 上海东方路下立交工程基坑上跨地铁2 号线
上海东方路N01 基坑为长26 m,宽18.1 m 的平行四边形基坑,开挖深度为6.5 m。上海地铁2 号线上行线以45°角从基坑下方穿过,隧道外径为6.2 m,衬砌厚度为0.35 m,环宽1.2 m,埋深为12.36 m,工程具体细节见陈郁[26]。根据徐凌[17]的研究成果,对于上海地铁2 号线盾构隧道的管片环纵向抗弯刚度折减系数可取0.7。可得管片环纵向抗弯刚度为6.7×108kN·m2,环间接头转动刚度为6.5×107kN·m/rad。根据黄栩等[3]研究成果,本工程土层Es3取24.63 MPa,ν取0.3。获得极限地层反力所需要的地基土变形值δu取0.1483 m,地基土不排水抗剪强度取70.37 kPa,竖向隆起系数Ncv取3.99。
文献[4]方法将地基和盾构隧道分别简化为Pasternak 地基模型和Euler-Bernoulli 梁。图14 为本文方法计算结果、Pasternak 地基-Euler 梁方法[4]计算结果与实测数据的对比曲线。由图可知,Pasternak 地基-Euler 梁方法[4]计算得到的隧道隆起范围明显大于实测数据,这应当是将盾构隧道视为连续梁高估了隧道的整体性所致。而相较于文献[4]方法,本文方法计算得到的盾构隧道隆起曲线更加接近实测数据,且整体变化趋势与实测数据一致,说明本文方法在预测隧道隆起变形方面更具优势。

图14 上海地铁2 号线计算结果与实测数据对比Fig. 14 Comparison of calculation results and measured data of Shanghai Metro Line 2
图15 为本文方法计算得到的盾构隧道环间接头张开量。由图可知,本案例管片环张开量与杭州延安路基坑下盾构隧道张开量的分布形态十分相似,但与上海闸北基坑下盾构隧道张开量的分布形态有较大区别。这三个案例的盾构隧道结构基本相同,基坑开挖深度也差别不大,最大的不同为基坑开挖范围,本案例基坑与杭州延安路基坑的长宽均未超过30 m,而上海闸北基坑的长宽均超过200 m,正是基坑开挖范围的巨大差异导致了盾构隧道张开量分布形态的不同。这种现象说明,不同规模的基坑引起的邻近盾构隧道的变形特点是不同的,在实际工程中应当采取不同的保护措施加以应对。
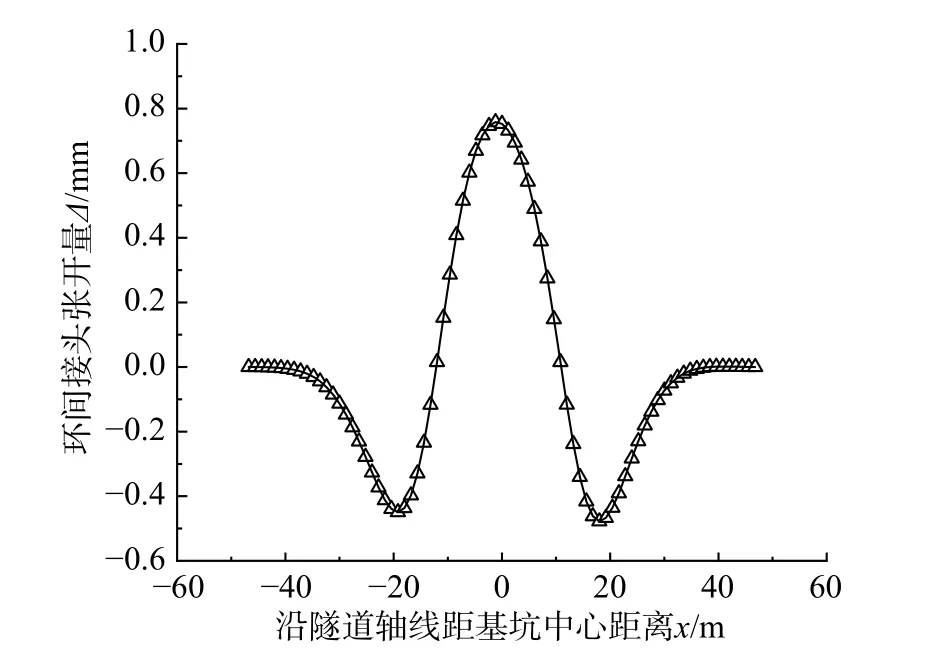
图15 上海地铁2 号线环间接头张开量计算值Fig. 15 Calculation value of joint opening between rings of Shanghai Metro Line 2
4 结论
结合非线性Pasternak 地基和带环间接头的盾构隧道计算模型,提出一种预测基坑开挖下既有盾构隧道隆起变形与内力的解析方法,主要结论如下:
(1)基于非线性Pasternak 地基模型和带环间接头盾构隧道计算模型,利用两阶段分析法,推导得到基坑开挖引起的邻近盾构隧道纵向变形与内力解析解答。
(2)通过与收集的三个工程实测数据对比,验证了所提预测盾构隧道变形计算方法的适用性和正确性,结果表明采用非连续接头模型考虑盾构隧道的隆起变形更接近实际情况。
(3)与前人理论结果进行了对比,所提方法将隧道简化为接头非连续的计算模型,充分考虑了接头的存在对隧道变形的影响,故而更加接近盾构隧道变形的真实状态。相较于所提方法,Pasternak地基结合Timoshenko 梁的方法高估了隧道的整体性,计算所得的弯矩和接头张开量明显偏小。
需要指出的是,所提出的带环间接头的盾构隧道计算模型仅考虑了环间接头的转动效应,忽视了接头处剪切效应的影响,在后续的研究中将进一步完善该模型。
