基于GRACE-FO的微波与激光星间测距数据的重力场模型对比分析

朱紫彤 闫易浩 梁 磊 穆庆禄 王长青 冯 伟,4 钟 敏,4

1 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077 2 中国科学院大学地球与行星科学学院，北京市玉泉路19号甲，100049 3 中山大学物理与天文学院，广东省珠海市大学路2号，519082 4 中山大学测绘科学与技术学院，广东省珠海市大学路2号，519082

随着卫星重力测量技术的发展，特别是GRACE与GRACE Follow-On(GRACE-FO)卫星计划的成功实施，为监测地球表面质量迁移提供了全新的视角，其产品广泛应用于水文学、地震学、海洋学和地球物理学等相关学科研究[1]。GRACE-FO是GRACE的后续卫星，两者原理基本一致，通过精确测量两颗卫星之间的距离变化率来反演地球时变重力场模型。相较于GRACE，GRACE-FO除搭载K波段微波测距系统(KBR, K-band ranging)外，还搭载激光测距系统(LRI, laser ranging interferometer)，可实现nm级星间测距精度，相较于μm级K波段微波测距系统，其精度至少可提高2个量级[2]。

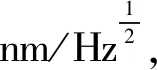
1 动力学法基本理论

1.1 反演流程

本文通过动力学法建立轨道及星间测距观测方程，采用最小二乘方法解算重力场系数。数据处理流程主要分为以下步骤[3]：1)以GRACE-FO Level-1B 数据及背景场模型作为输入数据，利用12阶Gauss-Jackson积分器计算积分轨道，与GPS实测轨道作差得到轨道残差；2)根据积分轨道计算星间距离变率参考值，与KBR或LRI观测数据作差得到星间距离变率残差；3)根据两类观测数据残差的中误差之比定权，再通过最小二乘方法求出时变重力场球谐系数。该过程使用的数据及模型见表1。

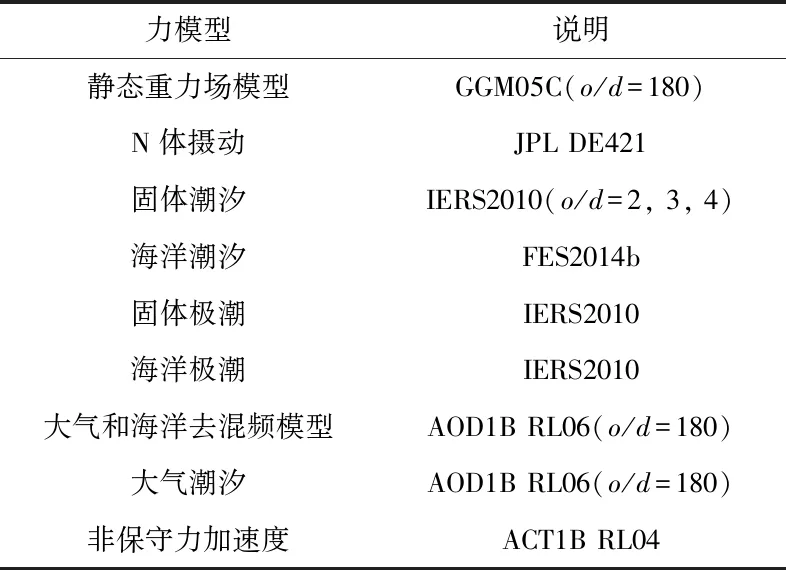
表1 重力场反演过程中使用的背景场模型

1.2 参数估计策略

与国内外多数重力卫星处理机构一样，本文采取24 h弧长，利用动力学方法求解90阶无约束地球时变重力场球谐系数。需要注意的是，GPS原始轨道数据为1 s采样，为确保重力场高阶部分的精度，本文将GPS观测值降采样至60 s。同时，对星间距离变率数据进行粗差探测，剔除RMS大于6倍中误差的弧段，从而提高重力场解的可靠性。重力场反演过程中需要估计较多参数，包括卫星初始状态参数、加速度计校正参数、星间测距经验参数等。受限于GRACE-FO卫星加速度计的影响，其加速度计数据校正策略与GRACE并不一致。设置星间测距经验参数与加速度计偏差参数每3 h估计1次，卫星初始状态参数按弧段每24 h估计1次，加速度计尺度矩阵及重力场参数按月估计。本文采用的参数估计策略如表2所示，下文将简单介绍引入的星间测距经验参数及加速度计校正参数。

在星间测距观测中，引入星间测距经验参数来吸收未模型化的摄动力及观测误差，其数学模型为[10]：

C+Dt+Etcos(u)+Ftsin(u)

(1)

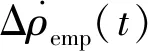
表2 重力场反演过程中参数估计策略

由于重力卫星加速度计数据产品中存在系统的仪器尺度因子和偏差漂移，因此在反演过程中必须对上述两类参数进行确定[11]。加速度计数据的校正在科学参考框架(science reference frame, SRF)下进行，其表达式为：

acal=Saobs+b

(2)

式中，acal为科学参考框架下校准后的非保守力加速度，aobs为原始加速度计观测值，S为3×3加速度计尺度矩阵，b为偏差参数。理想条件下，尺度矩阵S为单位阵。由于仪器缺陷导致加速度计轴之间相互影响，尺度矩阵还应包括非对角线元素。因此，本文给出尺度矩阵形式[12]：

(3)

该矩阵有3个对角线元素Sx、Sy、Sz，分别影响3个坐标轴加速度分量大小；α、β、γ为剪切参数，表示加速度计3轴之间在实际情况中由于非正交造成的影响；ζ、ε、δ为旋转参数，表示加速度计坐标轴与科学参考框架不重合产生的影响。

加速度计偏差参数b会随时间变化，本文采取如下校正形式：

b=C0+C1t

(4)

式中，C0、C1为待求参数，t为弧段起始处时间。在重力场反演过程中需要选择合理的加速度计校正策略，从而获得较优解。

2 结果分析与讨论

为探讨不同星间测距系统对重力场模型的影响，本文基于KBR和LRI数据分别计算2019-01～2021-08 GRACE-FO重力卫星时变重力场模型(APM_KBR与APM_LRI)时间序列，并与官方机构(center for space research, CSR)新发布的模型(基于KBR数据)进行对比分析，主要包括时变重力场模型、后验残差等。

2.1 时变重力场模型对比

当卫星机动或发生其他事件时均会引起LRI数据缺失，为评估相同条件(数据完整性及精度)下各模型解的精度，选取2019-05、2020-05、2021-05三个月(激光测距与微波测距均具有一致的数据连续性)结果的阶方差(以大地水准面高表示)，并与CSR模型进行对比(图1)。需要注意的是，时变重力场模型阶方差前30～40阶以时变信号为主，而高阶部分以噪声为主。由图可见，2019-05各模型信号量级符合较好，高阶部分的精度与CSR模型结果一致；2020-05各模型信号量级基本一致，但在40阶之后APM_LRI的精度变差。这是由于该月利用LRI数据反演重力场时，在粗差探测过程中剔除了3 d星间距离变率精度较差的弧段，导致该月APM_LRI略差于APM_KBR与CSR模型；2021-05与2019-05类似，各模型在信号、噪声等方面均基本处于同一水平。结果表明，在KBR和LRI数据都未缺失的条件下，反演得到的重力场模型精度水平一致。为方便比对，本文还选取2021-06重力场阶方差进行对比，结果如图2所示。如前文所述，LRI数据受卫星机动次数、载荷运行情况等影响较大，而该月GRACE-FO卫星机动及载荷异常事件较多，导致该月缺失13 d LRI数据[13]。从图2可以看出，由于缺失数据较多，APM_LRI从30阶之后噪声变大。另外，APM_KBR与CSR模型在30～70阶差别较大，说明在数据质量较差的情况下，重力场反演需要更精细的处理策略。

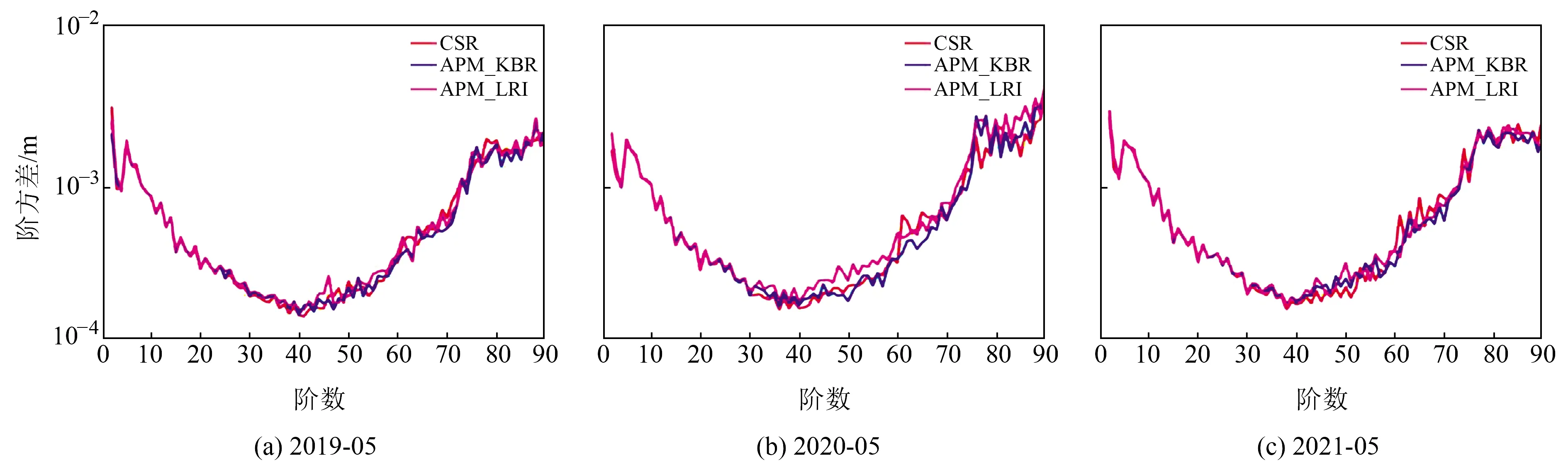
图1 2019-05、2020-05和2021-05各模型阶方差Fig.1 Degree variance of each model in 2019-05, 2020-05 and 2021-05, respectively

图2 2021-06各模型阶方差Fig.2 Degree variance of each model in 2021-06

此外，对2019-01～2021-08整个时间段重力场模型的质量异常趋势进行统计，结果如图3和4所示。在该过程中，由于空间分布存在较大的南北条带误差，因此本文采用如下后处理方式：300 km高斯平滑，扣除冰川均衡调整效应(glacial isostatic adjustment, GIA)，并替换重力场位系数中的质心项与C20项[14-16]。

从图3(a)～3(c)可以看出，两种模型在信号空间分布上与CSR模型基本一致，异常主要集中在南美洲地区、格陵兰地区和非洲中南部区域。从图3(d)和3(e)可以看出，APM_KBR和APM_LRI与CSR模型的差异主要集中在赤道附近，并且表现为条带状，该差异来源于后处理过程中未将条带现象完全消除。图4为两模型与CSR模型之差及两模型之差按地理纬度求得的标准差(standard deviation, STD)，可以看出，越靠近赤道附近，条带误差越大，模型的质量异常趋势差异越大；而标准差量级较小，均在1 cm以内。同时统计分析显示，APM_LRI的标准差略大于APM_KBR，推测其原因可能是APM_LRI中缺失较多星间距离观测数据，导致模型噪声较大。

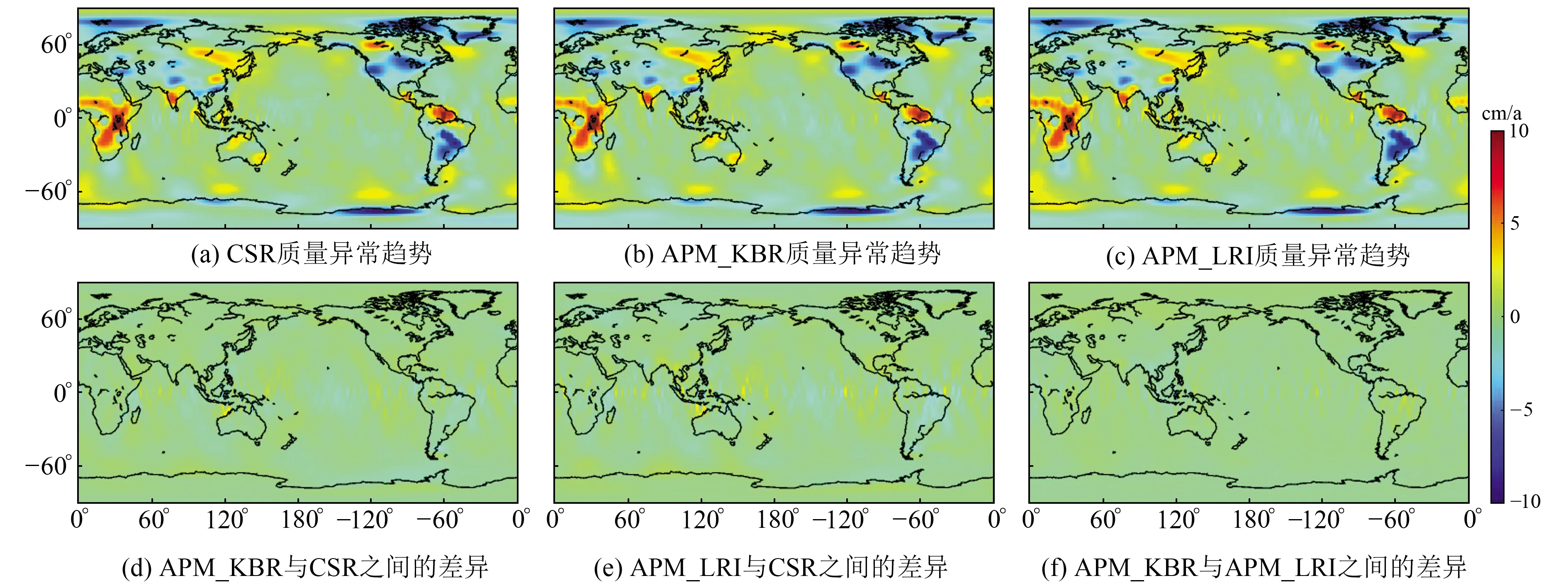
图3 CSR、APM_KBR与APM_LRI模型质量异常趋势及CSR、APM_KBR、APM_LRI之间差异Fig.3 Mass abnormal trend of CSR, APM_KBR and APM_LRI, and differences among these models

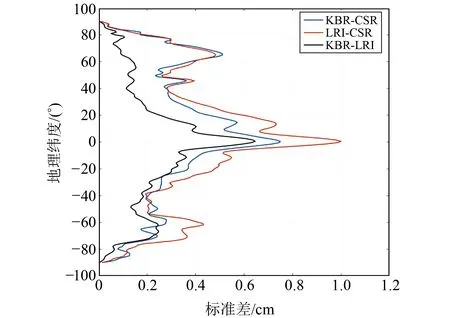
图4 按地理纬度统计的CSR、APM_KBR、APM_LRI之间质量变化趋势之差的标准差Fig.4 Standard deviation of mass change trend of the difference between APM_KBR, APM_LRI and CSR by geographical latitude

为进一步分析重力场模型在区域内的水文信号，选取亚马逊流域、格陵兰地区、长江流域及撒哈拉沙漠4个典型区域作为研究对象，分别计算模型在各个流域内水储量的时间序列，结果如图5所示。在亚马逊流域、格陵兰岛地区及长江流域各模型对应的水储量变化曲线具有较高的一致性，反映出各个时变重力场模型的信号幅值基本一致。撒哈拉沙漠地区的质量变化较小，其信号可在一定程度上反映重力场解算结果的噪声水平，对比该区域质量变化时间序列可以看到，APM_LRI在2021-06误差较大，这是由于该月LRI缺失13 d数据，使得2021-06激光数据解算结果精度较差。同时，本文还给出亚马逊流域、格陵兰地区、撒哈拉沙漠3个典型区域不同水文模式的数据统计(以等效水柱高表示)，用于量化各模型的一致性水平，结果见表3。分析发现，各模型周年振幅几乎一致，模型之间差异在0.1 cm以内；APM_KBR在格陵兰地区的趋势略小于另外2个模型，但差异也在0.1 cm左右；APM_LRI在撒哈拉沙漠的RMS略大于另外2个模型，结合图5可知是由于LRI数据缺失所致。

2.2 星间距离变率后验残差分析

在实际重力场解算过程中，后验残差中仍存

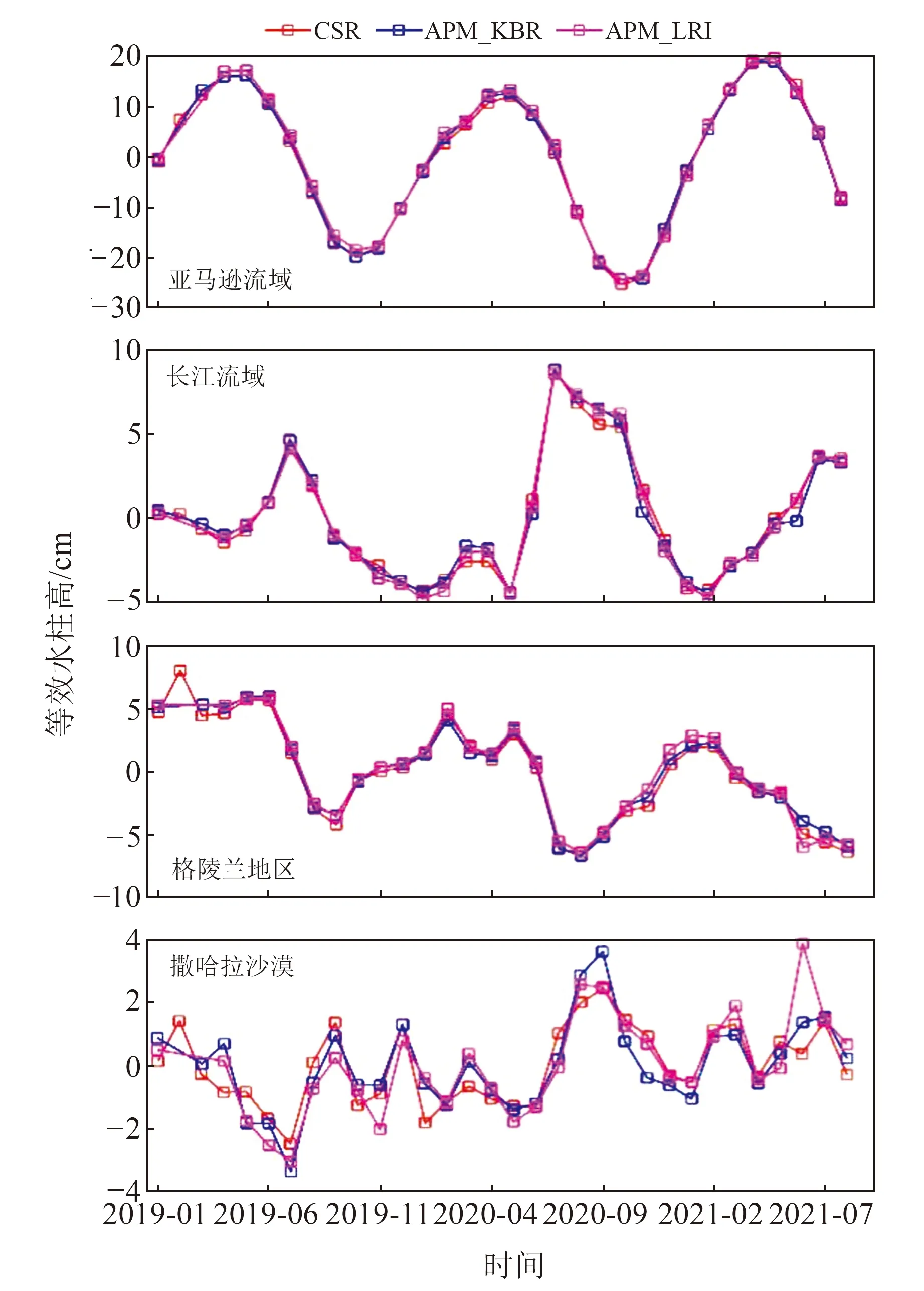
图5 各模型在4个典型区域内水储量变化时间序列Fig.5 Time series of water storage changes of each model in four typical regions

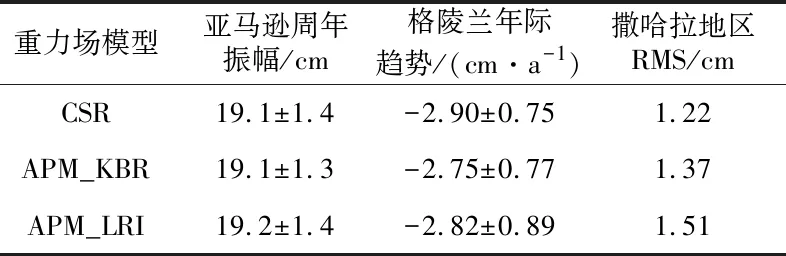
表3 各模型在3个典型区域的水储量变化统计

在背景模型中未充分描述的地球物理信号，其中包括比较典型的潮汐及非潮汐模型的混频误差等[3]。通过后验残差分析可以在一定程度上反映该月时变重力场解算质量及星间测距系统的测量精度，本文计算2021-05 KBR和LRI数据的后验残差，并分别在时域、频域下对其进行对比分析。需要说明的是，由于不同天之间的后验残差结果基本一致，为清晰地展示两类数据后验残差在时域下的特点，采用2021-05-01数据进行时域分析，结果如图6所示。可以看出，两类数据的后验残差量级均在±5×10-7m/s以内，但LRI精度明显高于KBR。LRI观测数据的后验残差整月RMS为 4.06×10-8m/s，KBR观测数据的为8.63×10-8m/s(见表4，单位10-8m/s)。另外，KBR后验残差存在较多毛刺，即高频噪声较大，而LRI后验残差的时间序列更平滑。因此，相比于KBR测距系统，激光测距观测数据具有更高的观测精度。此外，为提高样本选取的可信度，本文还随机选取并统计了2个月(2019-10、2020-07)星间观测数据后验残差的RMS(见表4，单位10-8m/s)。结果表明，APM_LRI后验残差的RMS比APM_KBR下降约50%。

图6 2021-05-01 KBR与LRI的后验残差时间序列Fig.6 Post-fit residuals time series of KBR and LRI measurements on May 1, 2021

表4 KBR与LRI后验残差RMS统计

进一步给出2019-10、2020-07和2021-05后验残差在频域下的对比情况(图7)，值得说明的是，由于GRACE-FO重力卫星绕地周期约为90 min，因此在该周期对应的频率下存在1 CPR(cycle-per-revolution)的非模型化摄动，而该影响会被星间测距经验参数所吸收(见式(1))。图7中黑色虚线为1 CPR频率，约为0.18 mHz，可以看出，该频段处2类观测的后验残差振幅很低，即1 CPR处部分非模型化的摄动被星间测距经验参数吸收。高频处(大于等于60 CPR) KBR后验残差的噪声大于LRI，这也与图6的结论相符合。因此，从KBR及LRI星间距离变率后验残差的角度来看，LRI的测量精度显著优于KBR。

最后对2021-05先验残差与后验残差的全球空间分布情况进行分析，结果如图8所示。从图8(a)和8(b)可以看出，APM_KBR与APM_LRI无论是信号分布还是量级差异均较小，这是因为先验残差中存在很强的非模型化摄动(1 CPR频率处)，会将其他质量变化信号湮没。而后验残差中(图8(c)和8(d))经过星间距离变率经验参数的拟合，非模型化的误差大幅降低(图7)，信号主要分布在亚马逊流域、非洲中部及南太平洋等区域。另外，APM_KBR高频噪声较大，在空间分布中呈斑点状，这也反映了LRI测量精度优于KBR。

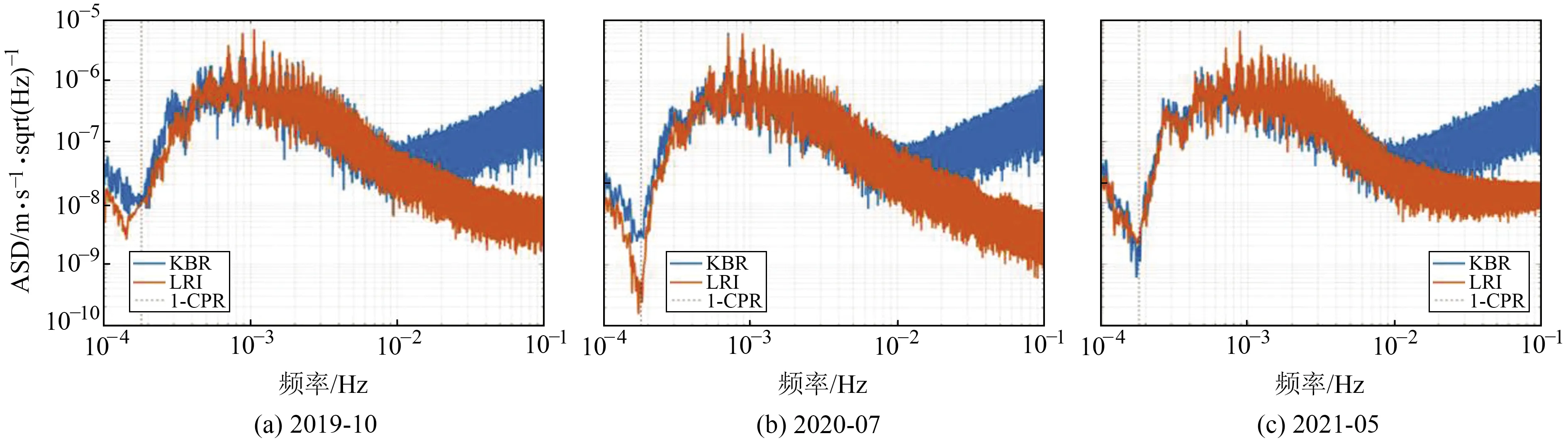
图7 2019-10、2020-07和2021-05 KBR与LRI的后验残差振幅谱Fig.7 The amplitude spectral of post-fit residuals of KBR and LRI measurements in October, 2019, July, 2020 and May, 2021

图8 APM_KBR与APM_LRI的先验残差与后验残差空间分布Fig.8 The spatial distribution of pre-fit and post-fit residuals of APM_KBR and APM_LRI

3 结 语

本文通过动力学方法，基于KBR及LRI数据分别解算2019-01～2021-08时变重力场模型，通过对时变重力场模型的阶方差、等效水柱高和后验残差进行对比分析，得出以下结论：

1)从单月解的精度来看，若KBR与LRI数据完整且质量较好，两类数据反演得到的重力场精度水平一致，但由于LRI数据受卫星机动、载荷运行情况等的影响，研究时段内有较多激光测距数据缺失；质量异常趋势项的空间分布及信号量级符合较好，其差异主要集中在赤道附近，应为重力场球谐系数中存在南北条带误差所致，统计显示最大差异不超过1 cm。相较于APM_LRI，APM_KBR与CSR模型的质量异常趋势一致性更好；各模型在亚马逊流域、格陵兰地区及长江流域的水储量变化时间序列一致性较好，但由于LRI在2021-06缺失较多数据，导致APM_LRI模型在该月精度较差，在撒哈拉地区质量变化的RMS大于APM_KBR与CSR模型。

2)KBR与LRI两类观测数据在2021-05的后验残差量级在±5×10-7m/s以内，后验残差分析结果表明，LRI精度明显优于KBR。同时，对时间序列进行分析发现，KBR后验残差中毛刺现象较多，而LRI的残差更平滑，其原因为KBR的测量噪声较大。从3个月的RMS统计结果来看，APM_LRI后验残差的RMS比APM_KBR下降约50%；振幅谱中两者在低频处差异较小，同时由于本文引入星间测距经验参数，在1 CPR处两者的后验残差被压制，高频处(大于等于60 CPR) KBR的后验残差噪声显著大于LRI；先验残差的空间分布中存在较大的非模型化摄动，导致两模型差异不明显，而后验残差中APM_KBR存在大量斑点，推测由KBR高频噪声所致。

通过对比分析可知，在数据完整且质量较好的条件下，基于LRI与KBR数据计算得到的重力场模型精度一致，激光干涉测距数据的高精度优势在时变重力场模型反演过程中并无体现，这主要是由目前背景场模型不完备及仪器噪声(主要源于加速度计)[17]共同导致，而参数策略的选取对重力场精度的影响同样不可忽略。另外，LRI的测量精度显著优于KBR，且高精度的星间测距系统对下一代重力卫星计划意义重大。研究表明[18-19]，可直接利用LRI Level-1B数据探测一些瞬时的质量变化，如地震、洪水、海啸等。此外，相比于KBR，LRI数据在高频区域(大于等于60 CPR)具有更高的信噪比，其观测精度优势在反演高阶地球静态场模型过程中或可体现。