SWOT宽刈幅干涉测高卫星数值模拟：以南海海平面变化监测为例

薛兆楠 冯 伟 陈 威 杨元元 闫昊明 钟 敏

1 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077 2 中国科学院大学地球与行星科学学院，北京市玉泉路19号甲，100049 3 中山大学测绘科学与技术学院，广东省珠海市大学路2号， 519082 4 广东省江门市住房和城乡建设局，广东省江门市江海一路83号，529040 5 盐城师范学院，江苏省盐城市希望大道南路2号，224007

近年来，新型雷达测高技术迅速发展。美国宇航局(NASA)、法国航天局(CNES)、英国航天局(UKSA)和加拿大航天局(CSA)等联合发起了SWOT(surface water and ocean topography)卫星任务，将为全球地表水及海洋表面的精确测量提供重要观测数据。SWOT卫星采用宽刈幅干涉测量方法提供15 km或更高空间分辨率的数据产品，从而表征海洋中尺度和亚中尺度动力现象[1]。SWOT也将用于观测全球面积大于250 m2的湖泊及宽度大于100 m的河流，以提供全球50%～60%的地表水时空变化信息[2]。

SWOT卫星计划于2022年发射，目前已有部分学者对SWOT卫星任务的观测能力进行了预估[3-5]。本文选取中国南海及其周边区域(2°～22°N，100°～120°E)，采用观测系统模拟实验方法(observing system simulation experiments，OSSE)对SWOT观测结果的精度等进行模拟分析[6]，并详细评估SWOT在整个南海地区不同空间和时间尺度上观测海洋现象的能力。

1 数据及模拟器介绍

1.1 SWOT卫星简介

SWOT卫星的核心载荷是Ka波段雷达干涉仪(KaRIn)，该仪器有两个合成孔径雷达 (SAR)天线，位于总长10 m的基线两侧(https:∥swot.jpl.nasa.gov/resources/media)，可测量地面幅宽60 km。由于雷达信号入射角存在一定的视角，SWOT观测数据在卫星下方存在20 km的空白，为此SWOT卫星将携带一个星下点传统微波高度计来填补，同时星下点高度计可用于校准和验证KaRIn观测数据[7]。星下点的传统测高方法依赖于返回波形前沿的功率和特定形状，并且由于大气的影响会导致信号在传播过程中出现衰减；而SWOT卫星采用的干涉技术依赖于测量2个雷达天线之间信号的相位差，从而大大提升了观测的空间分辨率。

图1对比了传统星下点高度计(以Jason-2为例)和SWOT卫星的21 d轨道覆盖范围(不包括星下点轨道)，可以看出，与Jason-2卫星约315 km的轨道间距相比，SWOT卫星的轨道覆盖范围提升显著。目前的大部分研究都是通过不同轨道的多颗测高卫星来观测获取二维海平面高度信息，可部分弥补高度计轨道间距过大这一缺点，而SWOT卫星将直接提供高精度、高空间分辨率的二维宽刈幅海洋信息[8]。

图1 21 d轨道覆盖范围Fig.1 21 d orbital coverage

1.2 海洋模式

本文使用的高分辨率海洋环流模式数据是由美国喷气推进实验室(Jet Propulsion Laboratory, NASA)发布的ECCO2产品，该产品采用麻省理工学院环流模式(MITGCM)，同化了海平面高度、洋底压力、表面风应力、海洋表面温度及海洋剖面温度盐度等观测数据。本文使用的是ECCO2产品中由Cube92模型输出的全球每日平均海平面高度(sea surface height，SSH)数据，空间分辨率为0.25°×0.25°。SWOT卫星预期达到的时间分辨率为21 d，本文选取2018-07-01～21的ECCO2 SSH数据进行模拟，为研究更长时间下SWOT卫星的观测能力，选取2018-01-01～07-19共计200 d数据进行分析。

1.3 SWOT海洋观测误差

本文在进行SWOT模拟时考虑的误差[9]包括：1)基线偏移误差，是由干涉仪基线长度发生变化而产生的。对于SWOT卫星，采用平面方式进行高程求解，基线长度为笛卡尔坐标系下YZ平面上2个天线连线的投影。2)KaRIn噪声，随到星下点的距离和有效波高的变化而变化。参考SWOT的相关文档，本文假设有效波高为2 m。3)相位误差，是由于2个雷达天线干涉信号路径之间的相位变化而产生的误差，与飞行系统和KaRIn组件有关。该误差主要由系统性相位误差和随机性相位误差组成，在模拟时认为与两条带之间的相位误差不相关。4)横滚误差，包括陀螺误差和横滚控制误差。由于该误差随着条带向外大致呈线性增长，从而造成SWOT观测的条带局部倾斜。SWOT携带高性能陀螺仪，能够测量旋转值从而减少横滚误差的影响。陀螺仪在测量旋转值时会存在一定的误差，而这一误差被考虑进SWOT模拟观测中。5)路径延迟误差，即卫星雷达信号在传播时受大气水分子、悬浮物及电子浓度的影响产生折射、散射甚至延迟，使所测距离与实际距离产生的偏差。由于Ka波段对水汽较为敏感，SWOT将搭载微波辐射计来探测水汽信息，从而降低水汽对Ka波段探测的影响。6)时间误差。卫星高度计是通过测量发射信号与回波信号之间的脉冲周期(时间间隔)计算距离，从而确定高程的，卫星在轨观测期间，卫星携带的时钟产生的频率漂移会使时钟脉冲周期发生变化，进而产生误差。

1.4 SWOT数据模拟

为获取SWOT模拟观测数据，本文使用JPL发布的SWOT模拟器(https:∥swot-simulator.readthedocs.io/en/doc-initiate_doc)，基于该模拟器，使用海洋模式SSH数据作为输入，加入仪器误差及路径延迟误差等影响因素，在沿轨的条带上生成SWOT模拟观测数据，并将模拟数据与输入的模式真值数据进行对比评估。首先以21 d的重访周期、77.68°的轨道倾角及891 km的卫星轨道高度为基本参数，模拟获得SWOT卫星的地面宽刈幅轨迹坐标，生成2 km分辨率的模拟沿轨迹网格。将每日海洋模式SSH数据插值到对应SWOT轨道网格中，得到SWOT时空域各轨道的SSH数据；加入随机生成的SWOT观测噪声，得到21 d时间分辨率及2 km空间分辨率的SWOT模拟观测数据。由于SWOT轨道特性等原因，会存在菱形的无观测值区域(图1(b))，需要对SWOT模拟观测数据进行插值和平滑。本文选用最邻近插值法填补菱形无观测值区域，为尽可能消除SWOT观测条带误差的影响，选用150 km的高斯滤波进行平滑。通过对比处理的SWOT观测数据与输入的海洋模式数据，本文对SWOT卫星在21 d和200 d时间尺度的观测能力进行了评估。此外，本文选取某一轨的SWOT模拟数据，进一步评估了SWOT观测亚中尺度海洋现象的能力。

2 结 果

2.1 SWOT海洋观测误差

图2显示了某一轨SWOT模拟SSH数据中各类误差和总误差的空间分布，可以看出，基线偏移误差(图2(a))、路径延迟误差(图2(e))和时间误差(图2(f))对SSH的影响明显小于相位误差(图2(c))和横滚误差(图2(d))。表1(单位cm)进一步给出了各项误差和总误差的统计结果，其中相位误差和横滚误差的标准差(STD)最高，对总误差的影响最大，但这2种误差会部分相互抵消，从最后的总误差(图2(g))中也可以反映出来。需要说明的是，图2中的沿轨方向存在宽度约20 km的观测空白条带，为星下点两侧各10 km的KaRIn载荷观测空白区。

图2 某一轨SWOT SSH观测数据Fig.2 One track of simulated SWOT observations

如图2(a)所示，基线偏移误差对称于星下轨迹，并且距离星下轨迹越远误差越大，这种分布与图2(d)的横滚误差相似，不同的是横滚误差两侧符号相反。图2(b)的KaRIn误差为随机误差，其空间分布呈噪点状，且该误差均值接近于零。如图2(c)所示，相位误差与基线偏移误差和横滚误差的对称性表现不同，基线偏移误差和横滚误差主要受卫星姿态影响，卫星两侧天线会一起发生变化，因此两条带之间存在相关性；而相位误差考虑仅受一侧天线的影响，两条带之间不存在相关性。相位误差作为影响较大的误差，在距离星下轨迹较远的位置误差最高约20 cm。如图2(d)所示，横滚误差随着时间的推移(即垂直星下轨迹方向距离的增加)线性增加，误差可达13 cm。如图2(e)所示，路径延迟误差在时间和空间上具有很大的变化性，这与大气水汽的空间不确定性有关。

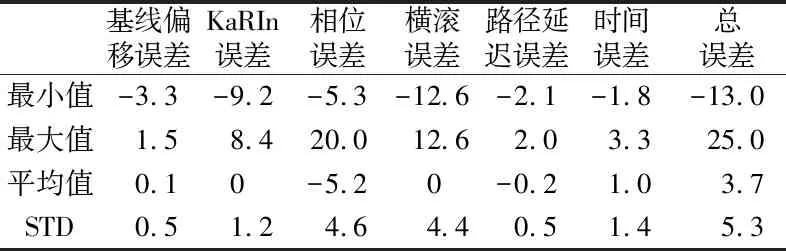
表1 某一轨模拟的SWOT SSH观测数据中各项误差和总误差统计

将21 d每条轨道生成的误差进行空间叠加，获得的误差分布如图3所示，相位误差与横滚误差较其他误差影响大，且误差向条带两侧增加，条带边缘处的误差最高，导致条带与条带交接处存在跳跃。而KaRIn误差和路径延迟误差由于具有随机性，在条带交接处不存在这类现象。图3(g)为总误差的空间分布，可以看出，其对SSH测量的影响最高可达30 cm。

图3 模拟器生成的21 d各误差空间分布Fig.3 The 21 d spatial map generated by the simulator

2.2 SWOT南海观测结果

将§1.2中海洋模式ECCO2输出的2018-07-01～21 SSH数据进行平均，得到SSH真值(图4(a))，并使用§1.4中SWOT 模拟器与§2.1中的模拟误差进行SWOT海洋观测数据模拟，得到中国南海区域21 d平均SWOT观测结果(图4(b))。需要说明的是，部分区域由于在21 d的周期内被多次覆盖，图4(b)中展示的是多次覆盖的平均观测数据，可以看出，模拟的SSH数据存在空间不连续现象，这与各轨道观测之间的时间滞后及轨道相关误差有关。对比图4(a)和4(b)可以看出，SWOT模拟观测信号与真实信号在大尺度空间分布上十分相似，但存在最大约30 cm的差异。经过二维高斯滤波(截断15 km)平滑处理后的SWOT观测数据(图4(c))与海洋模式之间的差异(图4(e))，和未经处理的观测数据与海洋模式之间的差异(图4(d))相比，条带状噪声得到有效去除，与真实信号的差异更小[10]。

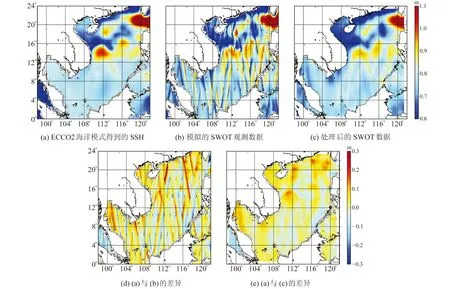
图4 中国南海区域各类数据结果Fig.4 Results of various data in the south China sea

进一步使用2018-01-01～07-19共计200 d的海洋模式真值数据对SWOT观测数据进行模拟。参考文献[3]，以1 d为步长，获取每21 d的SWOT观测空间分布，共得到179幅SWOT观测格网数据。图5(a)给出了该时间段未平滑的SWOT观测数据和平滑后的观测数据分别与对应海洋模式真值的均方根误差(RMSE)空间分布，由于SWOT以宽刈幅方式对海洋进行观测，条带之间的误差差异较大，均方根误差在条带交界处能达到20 cm，而条带中间(即星下点轨迹附近)区域的均方根误差相对较小，这也与图3(g)的结果一致。在该研究时间段，未平滑的SWOT观测数据与真值的均方根误差的平均值为4 cm。进一步对SWOT模拟数据进行二维高斯滤波(15 km窗口)平滑处理，海洋模式也作相同平滑[3]，如图5(b)所示，在经过空间平滑后，均方根误差虽然仍呈一定的条带状分布，但SWOT观测数据与真值的吻合程度有显著提高，均方根误差的平均值降低到2 cm。由此可见，空间平滑可以有效消除SWOT原始观测的部分误差，提高结果的可靠性。

图5 ECCO2海洋模式输出的SSH真值与SWOT模拟SSH结果的均方根误差Fig.5 RMSE between the SSH from ECCO2 ocean model and the SWOT simulator

本文计算了平滑后SWOT观测的标准差和海洋模式输出真值的标准差，结果如图6所示，SWOT观测能够很好地捕捉南海东北部和泰国湾等地海平面的显著变化信号。选择信号变化强度不同的3个区域：南海东北部(区域1，18°～22°N，116°～120°E，图6(a)黑框)、泰国湾(区域2，8°～12°N，100°～104°E，图6(a)绿框)和南海南部(区域3，8°～12°N，112°～116°E，图6(a)紫框)，获取SSH变化时间序列(图7)。如图6所示，南海东北部(区域1)和泰国湾(区域2)均存在较大的海平面变化信号，但图5(b)的误差空间分布表明，泰国湾的SWOT海平面观测误差明显小于南海东北部。由表2统计结果可知，南海东北部的SWOT海平面观测误差为1.2 cm，而泰国湾的误差为0.8 cm，这与海平面变化信号相对较小的南海南部(区域3)误差(0.7 cm)一致。结合图5(b)、6(a)和7可知，海平面变化信号本身的强度不会直接影响SWOT观测的精度，SWOT观测误差空间分布呈南北条带状，主要与其宽刈幅的沿轨迹观测模式有关，与原始信号强度没有很强的关联性。

图6 平滑后的SSH标准差Fig.6 The standard deviation of SSH

图7 3个区域海洋模式输出和SWOT模拟的SSH变化时间序列Fig.7 Time series of SSH anomalies from SWOT simulator and ECCO2 ocean model inthree regions

表2 3个区域SWOT观测和海洋模式模拟的SSH变化时间序列统计

2.3 SWOT沿轨观测结果

为进一步对SWOT观测亚中尺度海洋现象的能力进行评估，提取图4(b)SWOT模拟数据中某一轨(轨道编号135)的SSH数据，对该数据进行高斯滤波(半径15 km)和网格重采样(10 km×10 km)，并与2 km×2 km网格数据进行比较。如图8所示，加入了模拟噪声后的结果显示，SWOT卫星仍可较好地观测该区域海平面高度，其中图8(e)和8(f)为该轨道在2 km和10 km分辨率下SWOT模拟(图8(a)、8(c))与海洋模式(图8(b)、8(d))的差值。通过表3(单位m)可看出，2 km和10 km空间分辨率的SWOT模拟和海洋模式之间SSH差异的STD分别为0.03 m和0.02 m，相差不大。在2 km和10 km分辨率下，SWOT模拟SSH仍存在一定的噪声影响，但两者与海洋模式真值的接近程度类似。

表3 在2 km和10 km分辨率下SWOT观测和海洋模式模拟的SSH统计

图9为利用图8相应SSH数据计算得到的地转流流速。由于SWOT观测噪声的影响，在2 km分辨率下SWOT观测的地转流存在较大高频噪声，从而导致亚中尺度涡流无法被很好地区分出来(图9(e)中轨道南部地区)；而在10 km分辨率下，SWOT观测的地转流信号更加平滑，与海洋模式结果的空间特征也更为接近。表4(单位m·s-1)进一步对地转流流速进行了统计，在2 km空间尺度上，海洋模式和SWOT模拟观测的差异STD为0.11 m/s；而在10 km空间尺度上，二者差异显著降低，为0.06 m/s。由此可见，对于计算亚中尺度的地转流，相较于2 km分辨率，10 km分辨率的差值结果可显著降低SWOT观测误差的影响。

(a)2 km分辨率下SWOT模拟；(b)2 km分辨率下海洋模式；(c)10 km分辨率下SWOT模拟；(d)10 km分辨率下海洋模式；(e)SWOT模拟结果差异；(f)海洋模式结果差异图8 某一轨2 km及10 km分辨率下SWOT模拟和海洋模式的SSH结果及差异对比Fig.8 SSH from SWOT simulator and ocean model on SWOT interpolatedon regular 2 km×2 km and interpolated 10 km×10 km grids

(a)2 km分辨率下SWOT模拟；(b)2 km分辨率下海洋模式；(c)10 km分辨率下SWOT模拟；(d)10 km分辨率下海洋模式；(e)SWOT模拟结果差异；(f)海洋模式结果差异图9 某一轨2 km及10 km分辨率下SWOT模拟和海洋模式的SSH计算得到的地转流流速及差异对比Fig.9 Geostrophic current field based on SSH from SWOT simulator and ocean model on SWOT interpolatedon regular 2 km×2 km and interpolated 10 km×10 km grids

表4 在2 km和10 km分辨率下SWOT观测和海洋模式模拟的地转流流速的统计

3 结 语

本文使用OSSE方法模拟了SWOT观测数据，并与真实数据进行比较，从而评估SWOT在南海区域的海平面变化观测能力。与传统测高卫星相比，SWOT卫星采用宽刈幅干涉测量方式，能够直接进行二维观测，可以更好地获取海洋亚中尺度变化信息。未经处理的SWOT模拟数据存在条带状观测误差，空间滤波可有效降低观测误差，提高SWOT观测结果的空间连续性。

通过分析各类噪声的影响后发现，相位误差与横滚误差对SWOT的SSH观测结果影响较大，在南海区域能够达到20 cm和12.6 cm，且误差向条带两侧增加，距离星下点越远误差越大。SWOT模拟观测数据和海洋模式真值数据的均方根误差呈条带状分布，在条带交界处均方根误差可达20 cm，而靠近星下点区域的均方根误差很小。在研究时间段内，两者在南海的均方根误差平均值为4 cm，经过插值平滑后均方根误差平均值降低到2 cm。通过对比平滑后SWOT观测SSH的标准差和海洋模式真值的标准差发现，SWOT能够很好地反映出大部分SSH显著变化区域的信号。

进一步选取信号变化不同的区域进行比较发现，SWOT观测和海洋模式输出的SSH差异与信号强度无关，而受宽刈幅沿轨观测方式的影响较大。为研究SWOT观测海洋亚中尺度现象的能力，提取SWOT的一条轨迹(左右50 km条带)进行2 km×2 km和10 km×10 km网格比较后发现，SWOT模拟的2 km分辨率地转流信号受噪声影响较大，亚中尺度海洋现象无法被很好地分辨出来；而10 km分辨率信号经过平滑后更接近海洋模式的结果。

SWOT卫星有望于2022年发射升空，对SWOT进行模拟一方面可预先评估该卫星的观测能力，另一方面可为后续研究各类处理方法提供科学参考。后续将对SWOT探测中国南海区域年际和长期海平面时空变化的能力进行研究，以探讨SWOT卫星观测海平面变化的潜力。