智轨列车与常规公交共线组合发车间隔优化

陈维亚 ，李泽宇 ，张衡鹏 ，杨伟婷

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 轨道交通大数据湖南省重点实验室，湖南 长沙 410075)

近年来，智轨列车[1]作为一种投资较少、建设周期较短、速度较快的中运量新型路面公共交通工具，逐渐被引入到中等规模城市公共交通系统中，在具有较大客流的常规公交线路上替代常规公交独立运营或与常规公交共线共同运营。在共线运营模式下，如何优化智轨列车与常规公交的组合发车间隔以保障乘客和公交企业的共同利益成为值得研究的技术问题。公共交通发车间隔优化一直是众多学者的研究焦点。早期研究主要专注于考虑不同目标[2-3]或不同因素情况下[4-6]单车型公交模式下发车间隔的优化。为解决单车型公交模式下运力资源不足或浪费的问题，部分学者转向对多车型公交的发车间隔优化研究，并基于不同目标对常规公交发车间隔与车型配置进行了优化[7-8]。随着城市公共交通的快速发展，多种交通工具之间的运营组织协同优化问题逐渐成为学者的研究热点。针对常规公交与轨道交通工具的发车间隔优化问题，陈维亚等[9]以乘客出行及公交系统总成本最小为目标研究了现代有轨电车与常规公交换乘条件下的协调策略参数及组合发车间隔优化问题。田秀珠等[10]以最大化常规公交线路最小高峰小时平均满载率为优化目标对轨道交通共线段的常规公交发车间隔进行了优化。部分学者研究了在固定地铁线路、有轨电车线路下，基于不同优化目标对常规公交线路进行调整并在此基础上对其发车间隔进行了优化[11-13]。针对常规公交与快速公交的发车间隔优化问题，杨琦[14]在考虑快速公交与常规公交容量、速度差异的基础上研究了其在共线情况下以发车间隔优化为基础的公交专用道共享阈值区间的优化问题。谢昀珊[15]将车头时距的偏离值设置在一定范围内并以公交运营和乘客出行总成本最小为目标通过优化部分共线场景下快速公交和常规公交各线路的发车间隔促进二者的协调调度。魏平洪[16]假设公交停车时间为定值并以乘客出行成本和线路运营成本最小为目标，在优化公交发车间隔的基础上对快速公交接运的常规公交线路布设方案进行了优化。综上所述，早期众多学者对单车型公交发车间隔优化有着较为深入的研究，对常规公交与轨道交通工具之间的发车间隔优化问题集中于以提高换乘站点的换乘协调效率或优化线网为目标对常规公交与其他轨道交通工具之间的组合发车间隔进行优化；对常规公交与快速公交的发车间隔优化问题一般以公交企业与乘客出行的总成本最小为目标，为方便计算对部分因素进行了一定的理想假设，可以在模型中对部分因素进行考虑使得模型的求解结果更加贴近实际情况。因此，本文在前人研究的基础上，针对智轨列车与常规公交共线共站服务的较大客流场景，以乘客出行成本和公交企业运营收益为优化目标，考虑容量限制、行程时间随机性、发车间隔约束、首车发车时刻、超车过程和乘客拥挤费用等现实因素，建立了智轨列车与常规公交共线组合发车间隔优化模型。并结合算例，验证模型的有效性。

1 问题分析

1.1 问题描述

考虑一条具有K个站点的公共交通线路，乘客按照一定的到达率到达各站点，同时运行具有速度、容量、票价和运营成本等不同性质的智轨列车与常规公交，2种交通工具共用站点且均采用全程站站停的服务模式，车辆先到先服务。本文要解决的问题是：在考虑容量约束、行程时间约束和发车间隔约束等现实条件下，求得2种交通工具的最优发车间隔组合以达到乘客出行成本最小以及企业运营收益最大的目标。基于问题研究的严谨性，做出进一步假设：

1) 每辆智轨列车或常规公交的实际载客量均不允许超过其额定容量。

2) 智轨列车的站间行程时间视为恒定，常规公交的站间行程时间具有一定的随机性。

3) 2种交通工具均有其固定的发车间隔，且处于各自的最大最小发车间隔之间。

4) 不考虑乘客对车辆的选择行为。

1.2 运营过程分析

以图1所示的运行线路为例，对一些主要考虑因素及公交服务过程进行分析。

1.2.1 主要考虑因素

超车影响：由于智轨列车与常规公交的运行速度不同，因此在运行过程会发生超车，如图2所示，导致车辆对站点服务顺序的改变以及车头时距的变化。按照所有发出车辆到达站点k的时间进行排序，可得到每个站点车辆的服务先后顺序，车辆i到达站点k到达时间用ATik表示，前后2辆车的车头时距Hik可表示为：

公交行程时间随机性：智轨列车由于运行过程中受到外部干扰较少，实际行程时间Rik与预期行程时间μik视为相等，常规公交由于在运行过程中易受到多种因素的干扰，因此其行程时间在期望行程时间上下波动[17-18]，可表示为：

ξk是公交在站点k-1到k行程时间的正态分布扰动项。

1.2.2 公交服务过程

本文假定乘客到站服从Poisson分布且平均乘客到站率为λk，下车乘客人数服从二项分布且下车比例为ρk，车辆i离开站点k时车上人数为Lik，因此车辆i到达站点k时下车人数Aik：

考虑到车辆的容量限制，车辆i到达站点k时，在站点k等待上车的人数包括2部分：在车头时距Hik内到达的乘客以及由于前车满载未能上车的乘客数量UB(i-1)k：

当车辆i到达站点k时，公共交通车辆的剩余载客能力RCik可表示为：

本模型考虑了容量限制，因此在站点k候车的乘客中能够上i车的人数Bik可以表示为：

站点k未能上车的乘客可以表示为：

当车辆i离开站点k时车上人数Lik为：

在研究时段内智轨列车和常规公交的开行车辆数分别为M和N：

其中：T为研究时段的总时间长度；H1和H2分别代表常规公交和智轨列车的发车间隔。

服务时段内智轨列车与常规公交服务的总乘客数可表示为Fs：

2 模型构建

2.1 目标函数

当前大多数文献均综合考虑乘客利益和公交企业利益，因此本文考虑的目标是使乘客出行成本最小minCu以及公交企业运营收益最大maxC0。

2.1.1 乘客出行成本

乘客出行成本Cu包括乘客在车站等候上车时间成本Cuw和车内时间成本Cul，可表示为：

等候上车时间成本Cuw可表示为：

μw代表乘客等待时间价值系数。

车内时间成本包括乘客在乘坐公共交通车辆产生的时间成本以及由于拥挤产生的拥挤费用成本，可表示为：

式中：Ri(k+1)代表车辆i从站点k到达站点k+1的站间行程时间；μI代表乘客在车时间价值系数，可根据站点与在车乘客的年收入与年均工作时间[19]，计算出相应的μw与μI的取值；μc代表无座乘客的拥挤惩罚费用系数，且无座乘客的拥挤费用随着满载率的增加而增大，可看作是满载率的线性函数[20]，μc可表示为：

2.1.2 公交企业运营收益

本文考虑的公交企业运营收益C0是指运营票价收入Cup与运营时间成本Ct及运营里程成本CL的差值，可表示为：

运营票价收入Cup可表示为：

式中，Pi为车辆i的车费单价。

运营时间成本Ct是指公共交通车辆运营过程中与车辆折旧、维修和司机薪资等相关的成本，可表示为：

式中：LTi1和LTiK分别代表车辆i第1个站点的时间以及离开最后一个站点的时间；Gi代表车辆i的单位运营时间成本。

运营里程成本CL是公共交通车辆运营过程中与里程相关的油耗成本，可表示为：

式中：L代表线路的总长度；Fi代表车辆i的单位运营里程成本。

2.2 优化模型

本文建立了具有2个目标函数的优化模型，采用加权法将多目标函数转化为单目标函数，Tc称为系统总费用，可得本文建立的智轨列车与常规公交组合发车间隔优化模型如下：

式(20)为本文的目标函数，Tc越小表明系统效益越好，其中w1和w2分别为对应的权重系数，且w1+w2=1，根据乘客利益和公交企业利益的重要性选取不同的权重系数，本文参考相关文献的做法视乘客利益和公交企业利益同等重要[8-9,21]，w1=w2=0.5；式(21)～(23)以及式(2)共同构成本文的约束条件，式(2)为常规公交行程时间约束，式(21)为容量约束，式(22)为发车间隔约束；式(23)为权重系数约束。

3 求解算法

从上述公式的推导过程可知，在给定初始条件后，模型是传递和迭代的。可以通过使用结合递归和枚举的方法来求解。同时由于需要生成随机数来表示公交站间行程时间波动情况，本文在蒙特卡罗随机仿真条件下使用枚举和递归组合算法，利用matlab编程进行求解。结果会随随机数而波动，因此以多个计算结果的期望值作为最终结果。在循环结束后，找出最小函数值Tc及其相应的发车间隔以及其他目标函数值。

4 算例

4.1 实验线路描述

某公共交通线路上共18个车站，k=1, 2, 3,…,18。本文优化的周期为早高峰时段8:00～9:00，优化的总时长T=60 min；部分数据参考了文献[3]，每位乘客上车需要3.0 s，下车需要1.8 s，μw=0.143元/min，μi=0.165元/min，μ0=0.141元/min，w1=w1=0.5，全程长L=26 km，智轨列车和常规公交平均票价Pi分别为3元和2元，Ci分别为300人和80人，车辆单个乘客平均上下车时间分别为0.05 min和0.017 min以及0.01 min和0.03 min，Gi分别为5元/min和1.67元/min，Fi分别为4元/km和7元/km，发车间隔上下限分别为3 min和15 min及3 min和20 min，客流数据如图4所示。

4.2 优化结果与对比实验

为了求得该场景下的最优发车间隔组合，研究2种交通工具的首车发车时间差对2种交通工具的协同影响，同时探究同时开行2种交通工具相较于开行单一模式常规公交或智轨列车的系统总费用是否可以达到更优，本文建立了6组对比实验，6组对比实验的实验条件分别为：1） 仅开行常规公交；2） 仅开行智轨列车；3） 开行常规公交与智轨列车，不考虑二者的运营协同，各自以单独运营时的最优发车间隔进行发车；4） 开行常规公交与智轨列车，考虑二者的运营协同，不考虑二者的首车发车时间协同，即默认均为研究时段起点0时刻发出；5） 开行常规公交与智轨列车，考虑二者的运营协同及首车发车时间协同，常规公交从0时刻发出，智轨列车在其一个发车间隔时刻发出；6） 开行常规公交与智轨列车，考虑二者的运营协同及首车发车时间协同，智轨列车从0时刻发出，常规公交在其一个发车间隔时刻发出，实验结果如表1所示。

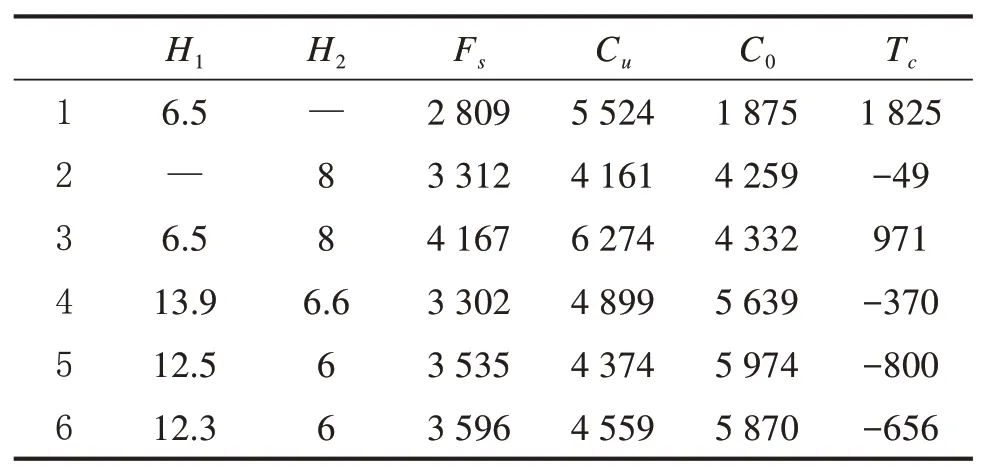
表1 实验结果比较Table 1 Comparison of experimental results

4.3 实验结果分析

对表1中6组实验的结果进行对比分析可以得出以下结论：

1) 将第3组结果与第4，5和6组结果进行对比分析，无论是否考虑首车发车时间协同，本文提出的组合发车模型下最优方案的系统总费用相较于单独运营智轨列车与公交时的最优发车间隔组合方案系统总费用更低，最优方案5相较于方案3可节省1 771元。方案3虽然也是通过本文模型计算出来的，但是由于是以各自的最优发车间隔方案运行而未考虑到二者的协同运营，因此也存在较多的串车现象使得乘客服务数量以及车辆利用率降低，从而使得系统总费用增加。

2) 将第1和2组结果与第4，5和6组结果进行对比分析可知，本文提出的组合发车模型下最优方案的系统总费用相较于单一常规公交、智轨列车模式下更低，表明该线路采取智轨列车与常规公交共线运营的方案相较于独立运营的方案更优。实验5相较于实验1和2系统总费用分别减少2 625元和751元，服务的乘客数分别提高25.8%和6.7%。原因是在单一常规公交模式下，车容量较小，因此需要减小发车间隔以满足乘客需求，因此大大增加了企业运营费用，但同时也需要考虑企业费用，不能一直减小发车间隔，因此导致服务的乘客数也不如其他组实验，同时由于票价较低，收入降低所以导致系统总费用较高，以上结果也反映了公交企业运营容易出现亏损，需要政府财政补贴的现状。

3) 将第4，5和6组结果进行对比分析，常规公交从0时刻发车，智轨列车延后发车的方案下，系统总费用最小，方案5相较于方案4和方案6分别减少430元和144元；方案5相较于方案4和方案6的系统总费用能够得到一定优化的原因在于初始时段线路积累的客流不多，而由于智轨列车的车容量比常规公交的车容量大很多，因此延后开行智轨列车可以运载每站积累的较多客流量，减少乘客滞留，同时由于智轨票价较高，可以提高企业收入从而使得系统总费用减少。因此，合理安排2种交通工具的首车发车时间可促进二者的运营组织协同，从而降低系统总费用。

4.4 灵敏度分析

客流是影响公交运营过程的主要因素之一，对其进行灵敏度分析，以研究在原客流的不同倍数下相关指标的变化情况。客流倍数对乘客出行成本、企业运营收益、系统成本影响如图5～7所示。

从图5中可知，在不同客流情况下，单一常规公交模式下的乘客出行成本总体上保持最大，且乘客出行成本Cu随着客流倍数增大而不断增大，相较于单独开行智轨列车以及优化后开行智轨列车与常规公交的2种模式有着更大的增长速度，因其相较于其他2种模式具有更小的车容量、更长的运行时间，因此当客流增大时，乘客等待时间成本和乘客在车时间成本有更大幅度的增加。而优化前的组合模式是智轨列车和常规公交单独优化时的最优发车间隔组合，虽然在发车数量上有所增加，但由于未考虑2种交通工具的运营组织协同，容易导致串车现象，因此乘客的出行成本也保持较高。

从图6中可知，在不同客流情况下，优化后组合模式下的公交企业运营收益C0与优化前组合模式下的相近，因为后者在开行的车辆总数上有优势，虽然增加了运营成本，但是运载的乘客数增多，因而公交企业运营收益得到提高；组合模式下的公交企业运营收益相较于单模式下的公交企业运营收益有较大的提高，原因在于优化后的组合模式下的方案由于考虑了车辆之间的运营组织协同，提高了2种交通工具的运输效率，在控制运营成本的同时提高了运营收入，因此总体上运营收益保持最大。

综合图5～7可知，客流量越大，本文提出的组合发车间隔优化模型的优化效果越好，且主要通过增加公交企业运营收益实现系统总费用优化。随着客流量增大，优化后的组合发车间隔模型最优方案下的乘客出行成本Cu虽然相较于优化前更高，但公交企业收益C0却有较大幅度的提高，总体系统总费用减小。单一常规公交模式下由于公交的容量、速度较小且票价较低，因此当客流不断增加时，其乘客出行成本的增长速度大于公交企业收益的增长速度，因此系统成本不断增加。

5 结论

1) 针对智轨列车和常规公交同站点共线运营的公共交通线路，提出了智轨列车与常规公交的组合发车间隔优化模型及求解算法。模型考虑了二者运行速度、容量、票价和运营成本等方面的差异性，以及发车间隔上下限、容量限制和公交行程时间随机性等现实因素，使得模型求解结果更加贴近实际情况。相较于其他模型，本文提出的共线组合发车间隔优化模型，能达到更优的效果，且随着客流量增大优化效果越好。

2) 以乘客出行成本最小和公交企业运营收益最大为目标兼顾了乘客和公交企业的利益，符合公交调度决策的思路；无座乘客拥挤成本的计算考虑到了乘客的出行感受，从某种程度上可提高公共交通的吸引力；考虑了首车发车时间对车辆协同的影响，证明合理安排首车发车时间可以促进二者之间的良好协同，从而降低系统总费用。

3) 本模型中，智轨列车与常规公交均只采用站站停的服务策略。为了进一步提高系统效益，可以进一步引入大站停等服务策略进行改进；此外，本研究主要优化多站点的静态调度计划，没有考虑动态旅行时间估计等因素，今后可以进一步探究动态调度问题。