基于超导电动悬浮车辆的动力学模型研究

张晓旭，张赛，马卫华*,，李腾飞，王自力，罗世辉

基于超导电动悬浮车辆的动力学模型研究

张晓旭1，张赛2，马卫华*,1，李腾飞1，王自力1，罗世辉1

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中国中车长春轨道客车股份有限公司，吉林 长春 130000）

相比于电磁悬浮，超导电动悬浮的超导磁体与轨道线圈之间的动态相互作用关系更为复杂，无法采用与电磁悬浮相类似的等效磁轨关系建立动力学模型。针对此问题，本文对超导电动悬浮车辆动力学模型建模方法进行了探究。首先，基于车辆悬浮系统的基本工作原理，利用有限元软件仿真计算得到不同速度及间隙下的二维磁力矩阵；其次，基于MATLAB组建数据库，借鉴曲面积分思想和极限理论，利用SIMULINK平台将离散化的二维磁力矩阵搭建成维关系矩阵，为后续超导电动悬浮车辆磁轨关系提供一定的基础；最后，基于多体动力学软件SIMPACK及其SIMAT技术完成SIMPACK与MATLAB的联合仿真模型。此外，通过对比分析系统固有频率验证了动力学模型的正确性，并利用所建立动力学模型分析了时速700公里系统的动力学响应，结果显示车辆运行各项动力学指标的仿真结果大小均在合理范围。本文工作可为今后超导电动悬浮列车动力学研究提供一定参考。

超导磁浮；电动悬浮；动力学模型；磁轨关系；维查表法

磁浮列车采用无接触悬浮的导向与驱动系统，具有速度快、能耗低、噪音低与安全舒适等优点，日渐成为轨道交通行业的研究热点[1]。在高速与磁浮技术并存的技术类型中，相比于电磁型悬浮技术，电动悬浮技术的磁浮车辆技术更为成熟，优势也更为明显。电动悬浮技术又分为永磁电动悬浮与超导电动悬浮；其中永磁电动悬浮技术是利用永磁体与轨道感应板相互作用产生悬浮力，时速可达到500公里，该技术目前仍处于试验阶段[2-3]；超导电动悬浮技术是利用超导磁体与轨道线圈间感应产生悬浮力与导向力，日本自20世纪70年代起开展了一系列超导电动悬浮技术研究，相比于永磁电动悬浮技术，超导电动悬浮技术研究更为成熟，且其悬浮间隙可达到100 mm以上，不需要附属控制单元就可以实现稳定的悬浮和导向[4-6]。因此对于发展高速及超高速轨道交通，超导电动制式悬浮更具优势。

由于超导电动悬浮列车的优越性能，各国学者开展了相关技术研究，超导电动悬浮基础理论研究也取得重要进展，美国HE等[7-8]、日本大桥俊介等[9]、意大利CARBONARI N等[10]运用动态电磁理论推导了超导电动悬浮系统的等效电路和电磁力表达式，并提出三维力解析模型；美国Davey K等[11]对超导磁体纵进行纵向谐波近似横向指数衰减，推导了车辆点头运动时的悬浮力与导向力；我国目前对于电动悬浮研究处于初级阶段，对超导电动悬浮型磁浮列车技术研究较少。万尚军等[12]、王志涛等[13]先后运用电磁理论建立动态电路模型分析了超导电动悬浮的基本特性。目前，除了日本学者外鲜有开展超导电动磁浮列车的动力学仿真分析，对于超导电动悬浮列车动力学模型也鲜有涉及[14]。因此开展超导电动悬浮车辆动力学模型研究，充分考虑超导电动悬浮导向系统的非线性，建立准确有效的超导电动悬浮车辆动力学模型，显得尤为重要。

针对上述问题，本文以某超导电动悬浮的磁浮车辆为研究对象，首先对其磁力特性进行分析，并基于超导电动悬浮工作原理和超导电动悬浮磁力的特性，建立了超导电动悬浮的磁浮系统动力学模型，通过对比分析模型系统的固有频率对所建立的动力学模型进行验证，最后利用所建立的模型对超导电动悬浮车辆动力学性能进行分析，为超导磁浮列车的电动悬浮系统动力学研究和悬浮架设计提供理论依据和应用参考。

1 电动悬浮系统结构与工作原理

超导电动悬浮系统如图1所示，主要包含U型轨道、悬浮架、车体等部件，其中悬浮架由超导磁体、构架、横梁、空气弹簧及连接装置等组成。U型轨道是整个系统的重要组成部件，为一些部件提供安装基础，例如其两侧对称安装有用于驱动的驱动线圈及用于悬浮导向的“8”字形零磁通轨道线圈。悬浮架是超导电动磁浮车辆车体与轨道连接的重要部件，悬浮架两侧安装有超导磁体。当列车前进时，车载超导磁体与轨道“8”字形线圈产生相互作用力，其垂直方向产生一个向上的分力用于支撑列车起悬浮作用，水平方向分力用于控制列车左右运动起导向作用。车体是承载的重要部件，其作用是承载乘客及各种设备，同时起到磁屏蔽作用，避免列车乘客受到电磁辐射影响。

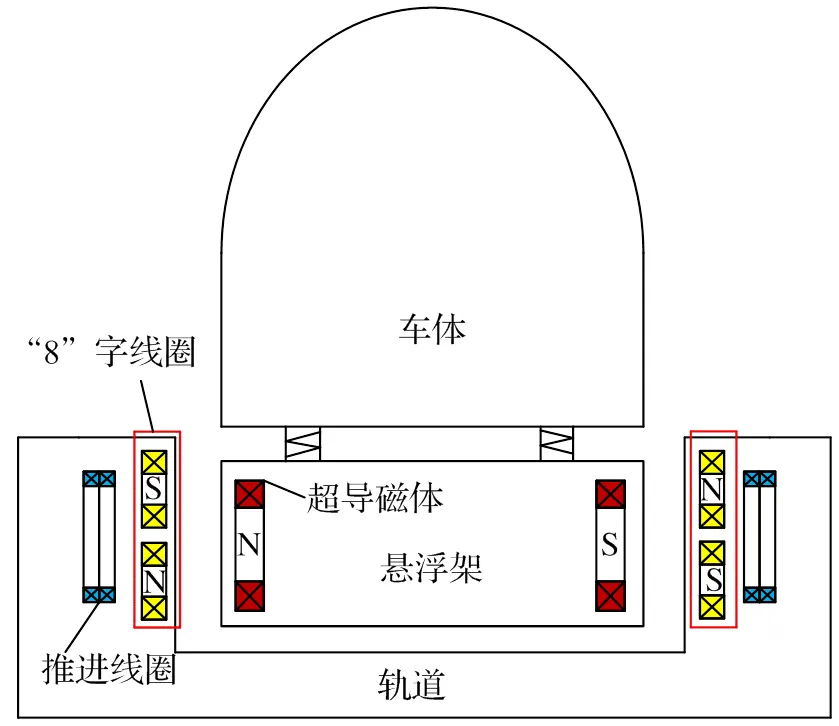
图1 电动悬浮列车截面图

超导电动悬浮原理如图2所示。图2（a）为超导电动悬浮拓扑结构，系统由零磁通线圈和超导线圈组成，零磁通线圈通过铰链线连接。图2（b）为悬浮与导向原理示意图，车辆前进时带动超导磁体前进，从而引起“8”字形线圈中磁场的不断变换产生感应电流。由于线圈上下两环为交叉环绕，感应出的电流方向相反，当超导体位于中间位置时上下环路内电流大小相同，当超导磁体向下移动时两环路内感应电流大小不同，从而引起线圈内有电流通过，相互作用产生悬浮力。水平方向上，由于两侧的零磁通线圈通过铰链线连接，当车体偏离轨道中心线时两侧线圈感应电动势不同，相连的线圈会产生电流，靠近超导磁体的一侧会产生斥力，远离超导磁体的一侧产生吸引力，最终合力推动车辆向轨道中心位置靠近。

2 超导电动悬浮磁力特性分析

本文利用有限元软件，借鉴曲面积分思想和极限理论，将其划分成微段，每一微段等效线性化，求得微段节点的磁力值，其余位置磁力值采用差值计算，求得同一速度下系统对应位置的磁力，通过计算得到悬浮力、导向力与磁阻力如图3所示，可以发现，随着垂向位移的增加，悬浮力与导向力呈逐渐增大趋势；随着横向位移的增加，悬浮力、导向力与磁阻力均不断增大；此外，悬浮力、导向力与磁阻力随纵向位置的变化呈周期性正弦变化。

3 动力学模型建模方法研究

对超导电动悬浮车辆磁力特性分析可以发现其力学特性受悬浮间隙、导向间隙、纵向运行速度与纵向相对位置四方面因素影响，具有的非线性，想要建立更为细致的描述列车运行状态的动力学仿真模型，关键是要解决列车建模过程中的超导磁体与轨道线圈间磁力特性的正确表达，从而建立完整的动力学模型，实现超导电动悬浮车辆的动态仿真分析。

3.1 磁轨关系处理

建立超导电动磁浮车辆动力学模型，首要问题是解决磁轨关系，其中电磁型磁浮系统的磁轨关系处理主要分为两种[15-16]：一种是考虑悬浮控制算法，建立包含控制算法实现车轨相互作用，称之为悬浮控制法；另一种则是将非线性主动控制力等效简化为弹簧阻尼力，称之为弹簧阻尼法。本文所研究的超导电动悬浮系统不包含主动控制，且由第2.3节磁力分析可以发现，超导电动悬浮系统具有很强的非线性，不宜直接线性化处理。因此利用MATLAB组建数据库，在SIMULINK建立维查表法框图，创建与SIMPACK接口，从而可实时获取超导电动悬浮系统的位置与速度，传递至SIMULINK利用查表法获取对应的悬浮力、导向力与磁阻力，从而完成磁轨关系的确立，如图4所示。

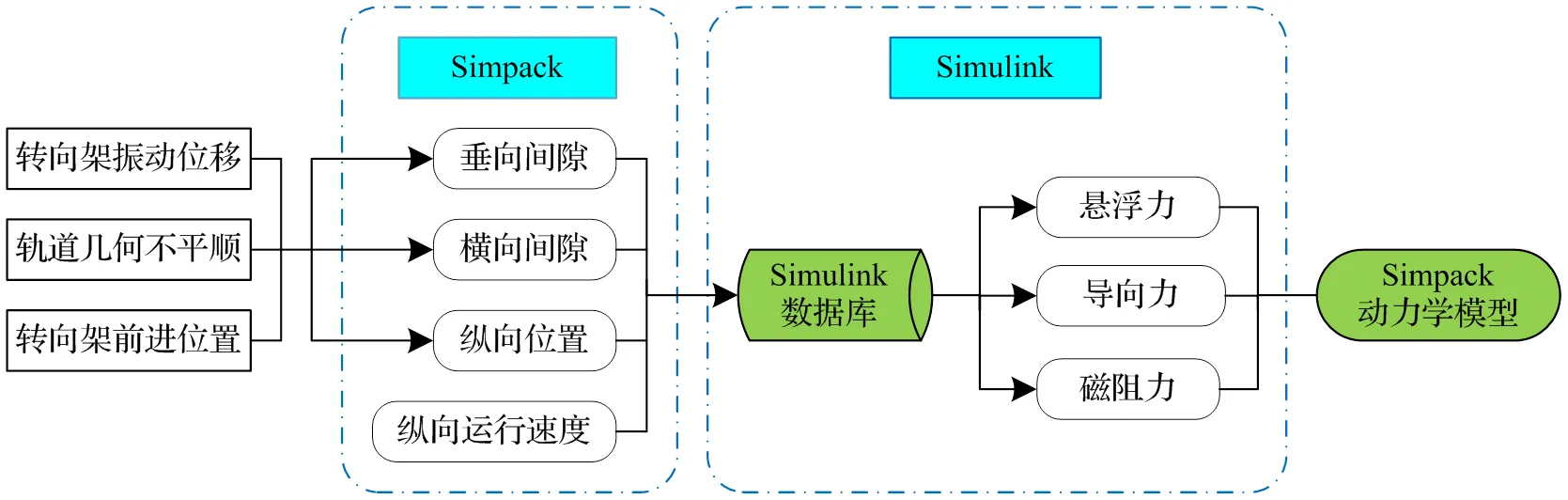
图4 磁轨关系处理流程图

维查表法的具体原理如图5所示，通过Simulink中的n-D Lookup Table模块计算一个函数的变量采样表示形式为＝(1,2, …, x)，其中函数可以是经验函数。此模块函数通过查找或插入使用模块参数定义的值表，将输入映射到输出值。在查表法中，第一个输入标识第一个维度（行）断点，第二个输入标识第二个维度（列）断点，依此列推。

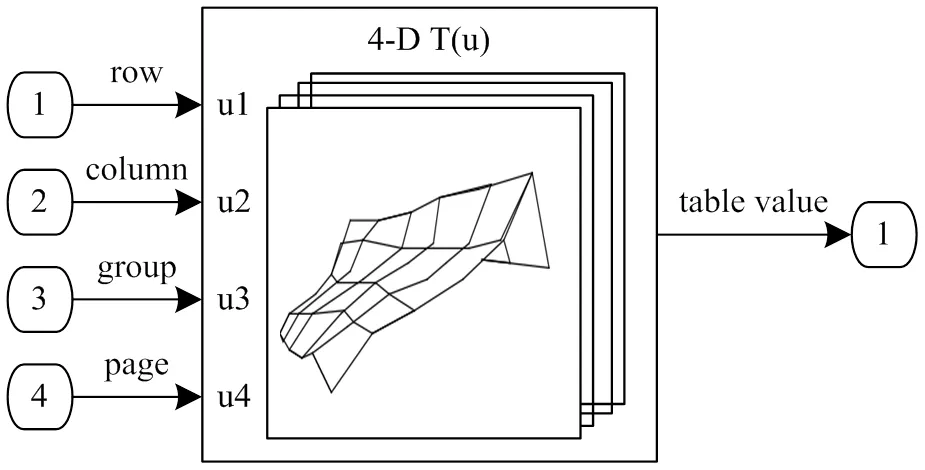
图5 n维查表法示意图

3.2 动力学模型建模

本文以SIMPACK为例介绍超导电动磁浮系统的动力学建模方法。首先确定研究对象，本文研究对象为超导电动磁浮车辆，悬浮系统的基本结构主要由超导磁体、构架、横梁、一系悬挂装置、二系悬挂装置、牵引拉杆等组成。超导磁体与U型轨道推进线圈通过直线电机作用产生纵向牵引力传递至构架，再通过牵引拉杆牵引车体前进；横向力由于构架与超导磁体之间的一系悬挂装置，所以由超导磁体产生的横向力经过一系装置传递至构架，再通过二系悬挂装置传递至车体；在车辆完全起浮后，超导磁体与轨道线圈之间产生的垂向力由超导磁体传递至构架，再经由二系空气弹簧装置传递至车体。根据超导电动悬浮列车结构组成与力的传递过程，利用SIMPACK建立列车动力学仿真模型如图6所示，主要参数如表1所示。

4 模型验证与仿真分析

采用建立的磁浮车辆动力学模型，施加如图7所示的地面垂向不平顺样本，开展超导磁浮车辆动力学仿真分析计算。首先进行动力学模型验证，然后计算车辆以速度700 km/h直线运行时的垂向和横向动力学响应。

图6 动力学模型示意图

表1 动力学主要建模参数

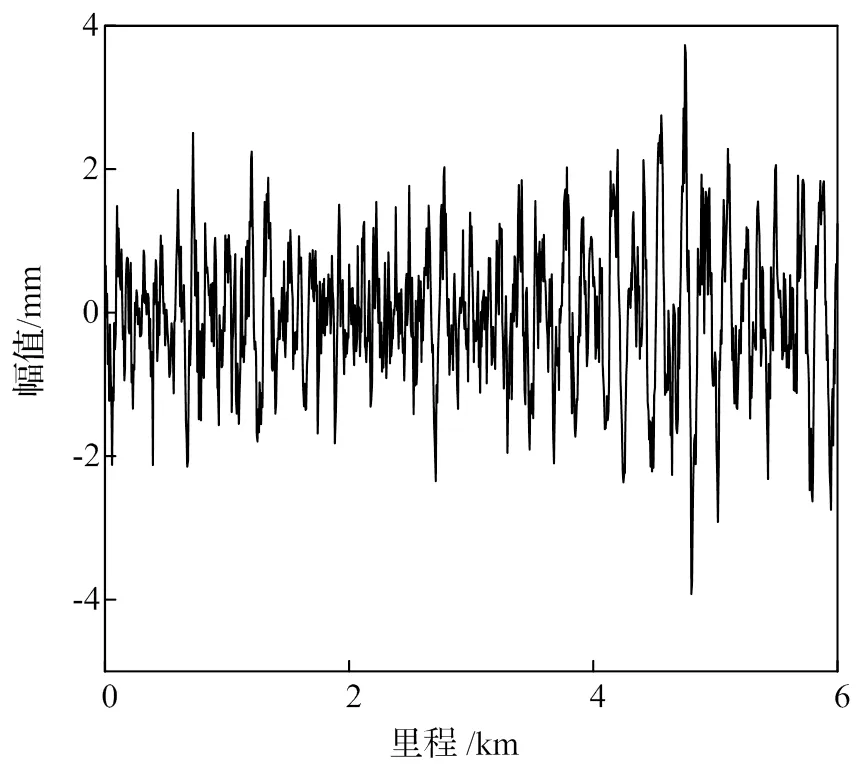
图7 轨道垂向不平顺变化图

4.1 模型验证

首先对超导电动悬浮系统结构进行简化，得到超导电动悬浮系统的垂向振动力学模型如图8所示，系统参数说明如表2所示。

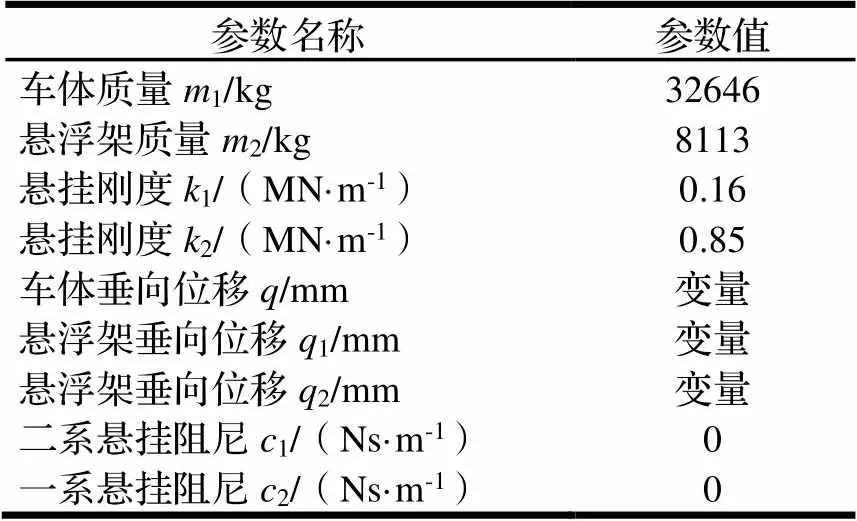
表2 系统主要参数

车体的浮沉方程为：

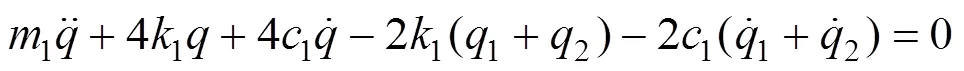
悬浮架的浮沉方程为：

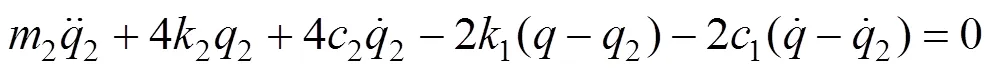
单独计算车体浮沉自振频率时，可将悬浮架认为是静止的；同理单独计算悬浮架浮沉自振频率时也认为车体是静止的。不考虑各刚体运动的耦合作用以及悬挂系统的阻尼[17]，则车体与悬浮架的浮沉方程可简化为：

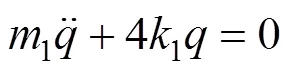
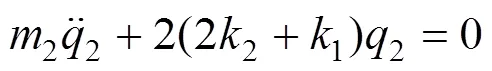
车体与悬浮架的浮沉频率计算公式为：

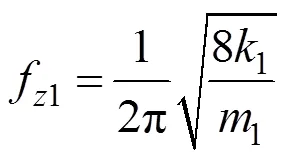
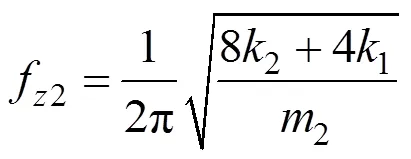
将表2中数据代入得到，系统中车体的浮沉固有频率为0.98 Hz，悬浮架的浮沉固有频率为4.81 Hz。同时利用所建立动力学模型进行分析，当超导电动悬浮车辆以700 km/h速度直线运行时车体垂向加速度响应时程曲线如图9（a）所示，可见，当采用非线性电动悬浮系统时车辆垂向振动加速度响应最大值为1.16 m/s2，且其响应波形与不平顺变化趋势基本一致。此外由图9可见，车体垂向加速度主频为0.99 Hz，与车辆的浮沉固有频率接近，同时悬浮架浮沉固有频率4.83 Hz在频谱中也有显示，说明仿真模型的建立是正确可行的。

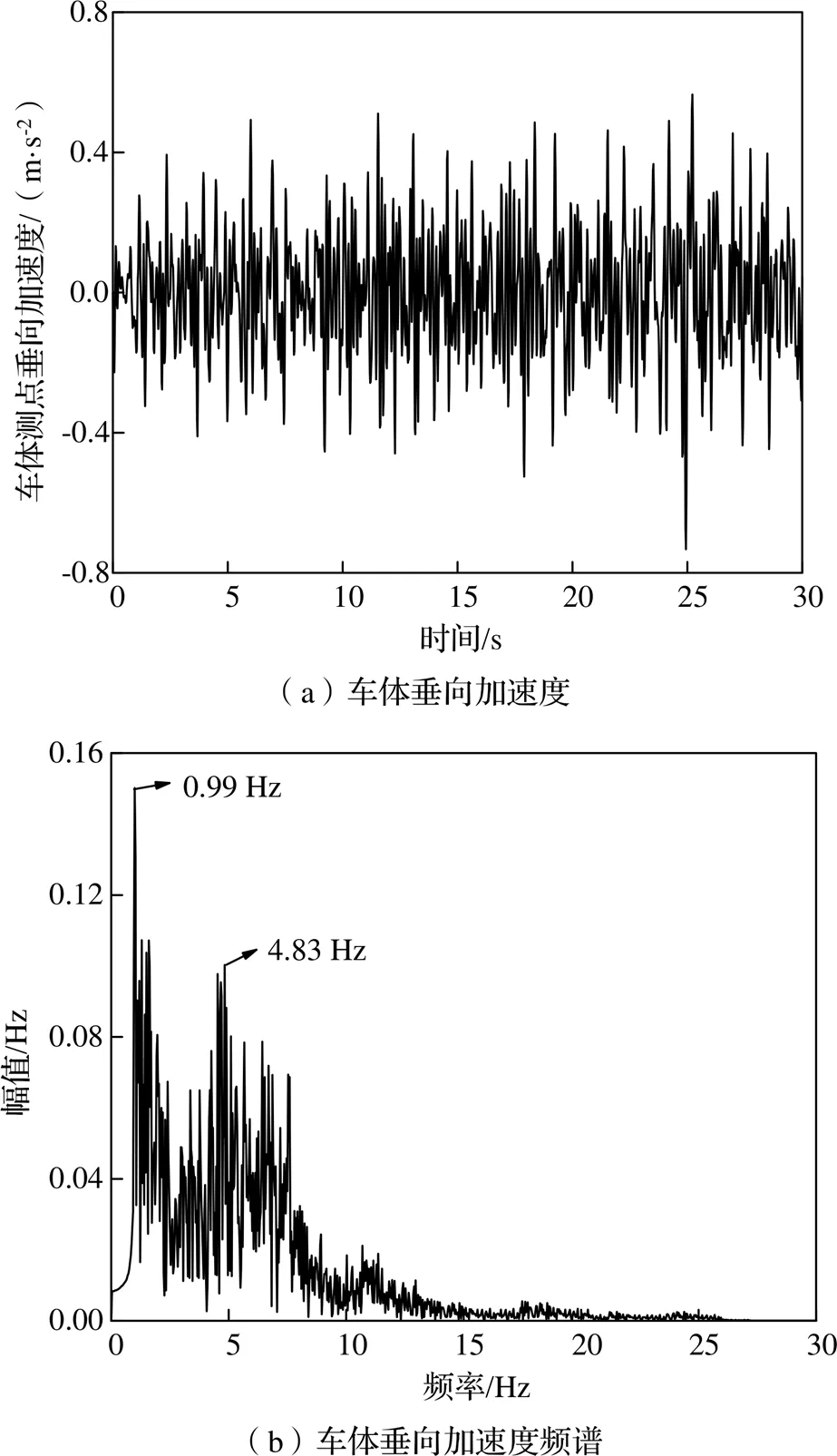
图9 车体垂向运动特性分析

4.2 仿真分析

根据所验证的动力学模型，研究超导电动悬浮车辆的动态响应特性，验证超导磁浮车辆系统的稳定性，重点分析了车辆Sperling平稳性指标值、悬浮间隙最大值、空气弹簧垂向力和垂向位移。

超导磁浮列车以速度700 km/h运行时，垂向Sperling指标值为2.45，横向Sperling指标值为2.25。其余各项动态指标如图10、图11所示：空簧垂向力主要在40 kN左右变化，最大值40.84 kN；空簧垂向位移主要在0.8 mm左右变化，变化值最大1.55 mm；悬浮力主要在32.5 kN左右变化，最大值34.24 kN；悬浮间隙变化值主要在1 mm左右，最大值2.49 mm，各项指标均在合理范围内。通过动力学分析进一步验证了仿真模型的正确性，同时表明超导电动悬浮车辆运行平稳性符合要求。

图10 二系空簧垂向特性

5 结论

本文以超导电动悬浮车辆为研究对象，对其动力学模型进行探究，得到如下结论：

（1）电动悬浮系统磁轨关系可采用维查表法，基于MATLAB组建数据库和SIMULINK平台，将离散化后的磁力、速度和间隙的关系曲线搭建成维查表法框图，然后利用SIMAT技术与多体动力学软件SIMPACK建立接口，解决超导电动悬浮车辆磁轨关系；

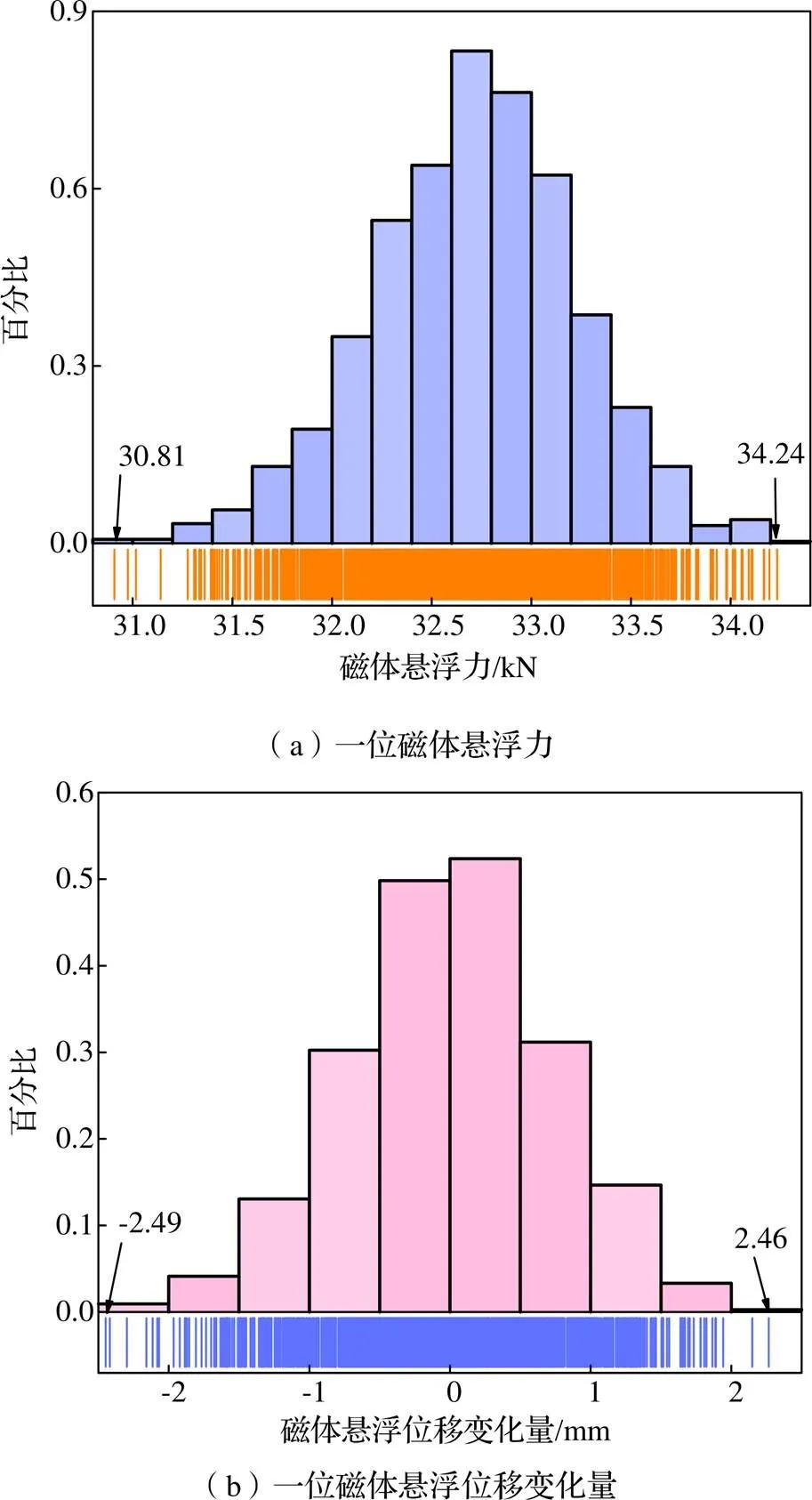
图11 一位磁体悬浮特性

（2）通过对比动力学模型计算和理论推导下车辆车体与悬浮架的固有频率数值，验证了永磁电动悬浮磁轨关系和动力学模型的正确性，为后续动力学分析提供一定的基础；

（3）超导电动悬浮车辆以速度700 km/h运行时，其运行平稳性及各项动力学指标均符合标准要求，进一步验证了模型建立的正确性。

[1]徐飞，罗世辉，邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报，2019，41（3）：40-49.

[2]熊嘉阳，邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报，2021，21（1）：177-198.

[3]过振宇，杨杰. 永磁悬浮轨道侧向力控制系统的DMC-PID控制策略[J]. 铁道科学与工程学报，2021，18（6）：1371-1381.

[4]马光同，杨文姣，王志涛，等. 超导磁浮交通研究进展[J]. 华南理工大学学报（自然科学版），2019，47（7）：68-74，82.

[5]张娟，赵春发，冯洋，等. 超导磁浮列车电动悬浮导向力学特性研究[J]. 机械，2020，47（9）： 25-32.

[6]Kyotani Y. Recent progress by JNR on Maglev[J]. IEEE Transactions on Magnetics，1988，24（2）：804-807.

[7]He J L，Rote D M，Coffey H T. Applications of the dynamic circuit theory to Maglev suspension systems[J]. IEEE Transactions on Magnetics，1993，29（6）：4153-4164.

[8]He J，Coffey H. Magnetic damping forces in figure-eight-shaped null-flux coil suspension systems[J]. IEEE Transactions on Magnetics，2002，33（5）：4230-4232.

[9]Carbonari N，Martinelli G，Morini A. Calculation of levitation，drag and lateral forces in EDS-MAGLEV transport systems[J]. Archivfür Elektrotechnik，1988，71（2）：139-148.

[10]Ohashi S. Weight Reduction of the Damper Coils in the Superconducting Magnetically Levitated Bogie[J]. IEEE Transactions on Magnetics，2018（11）：1.

[11]Davey K，Morris T. Calculation of motion induced eddy current forces in null flux coils[J]. IEEE Transactions on Magnetics，1995，31（6）：4214-4216.

[12]万尚军，钱金根，倪光正，等. 电动悬浮型磁悬浮列车悬浮与导向技术剖析[J]. 中国电机工程学报，2000，20（9）：23-26，32.

[13]王志涛，蔡尧，龚天勇，等. 基于场－路－运动耦合模型的超导电动悬浮列车特性研究[J]. 中国电机工程学报，2019，39（4）：1162-1171.

[14]张娟. 超导电动悬浮磁力特性及超导磁浮车辆动力学仿真分析[D]. 成都：西南交通大学，2020.

[15]Rote D M，Cai Y. Review of dynamic stability of repulsive-force maglev suspension systems[J]. IEEE Transactions on Magnetics，2002，38（2）：1383-1390.

[16]梁鑫，马卫华. 2种磁轨关系的磁浮车桥相互作用比较分析[J]. 铁道科学与工程学报，2017，14（4）：845-851.

[17]曾京，邬平波，郝建华. 铁道客车系统的垂向减振分析[J]. 中国铁道科学，2006，27（3）：62-67.

Dynamic Model of Superconducting Electric Levitation Vehicle

ZHANG Xiaoxu1，ZHANG Sai2，MA Weihua1，LI Tengfei1，WANG Zili1，LUO Shihui1

(1.State Key Laboratory of Traction Power, Southwest Jiaotong University,Chengdu 610031,China; 2.CRRC Changchun Railway Vehicles Co.,Ltd., Changchun 130000, China)

Compared with the Electromagnetic Suspension Maglev, the dynamic interaction relationship between the superconducting magnet and the orbital coil of the superconducting electric levitation is more complicated, and the dynamic model cannot be established by using the equivalent magnetic orbit relationship similar to the Electromagnetic Suspension Maglev. Aiming at solving this problem, this paper explores the modeling method of dynamic model of superconducting electric levitation vehicle. Firstly, based on the basic working principle of the vehicle suspension system, the finite element software is used to simulate and calculate the two-dimensional magnetic matrix under different speeds and gaps. Secondly, a database is established based on MATLAB, and the surface integration idea and limit theory are used for reference. The two-dimensional magnetic force matrix is built into an n-dimensional relationship matrix, which provides a certain basis for the magnetic track relationship of the subsequent superconducting electric levitation vehicle. Finally, the co-simulation model of SIMPACK and MATLAB is completed based on the multi-body dynamics software SIMPACK and its SIMAT technology. In addition, the correctness of the dynamic model is verified by comparing and analyzing the natural frequency of the system, and the dynamic response of the system at a speed of 700 kilometers per hour is analyzed by using the established dynamic model. The simulation results of various dynamic indicators of vehicle operation are all within a reasonable range. The research provides reference for future study on dynamics of superconducting electric levitation vehicle.

superconducting maglev；electric levitation；dynamic model；magnetic orbit relationship；n-d look-up table method

U237

A

10.3969/j.issn.1006-0316.2022.10.006

1006-0316 (2022) 10-0035-08

2022-02-25

国家自然科学基金面上项目（51875483）；牵引动力国家重点实验室自主研究课题（2020TPL_T04）

张晓旭（1996-），女，河北石家庄人，硕士研究生，主要研究方向为列车系统动力学，E-mail：zhangxiaoxu1225@163.com。

马卫华（1979－），男，山东滕州人，博士，研究员，主要研究方向为机车及重载列车动力学、磁浮列车悬浮架设计及列车动力学，E-mail：mwh@swjtu.edu.cn。