基于最优Bohman窗的改进S变换电能质量扰动特征精确快速提取方法

袁莉芬 张成林 尹柏强 李 兵 佐 磊

(合肥工业大学电气与自动化工程学院 合肥 230009)

1 引言

随着电网建设的不断推进，各种非线性用电设备的增加以及可控硅整流装置和调压装置的广泛使用，电力系统中开始出现大量谐波和超高次谐波；大型变压器空载激磁和大负荷投切引起的20 ms以内电压短时扰动也是值得关注的问题。电能质量扰动不仅会造成电能的浪费，电力设备发生故障严重时还可能会引发重大事故[1,2]。为此，部分用户对电能质量提出了更严格的标准，这对电能质量扰动的检测也提出了更高的要求。因此，对于电能质量扰动特征的精确快速提取，将成为有效治理和评估电能质量问题的重要依据。

电能质量扰动特征包括时域特征和频域特征[3]。傅里叶变换[4,5]是频谱分析的重要工具，可以成功提取信号的频域特征但无法获得时域特征，因此仅适用于平稳信号的分析。为了同时获得信号的时频域特征，逐渐发展出以下几种时频分析方法：短时傅里叶变换(Short Time Fourier Transform, STFT)[6–8]、小波变换(Wavelet Transform, WT)[9–11]、S变换(S-Transform, ST)[12–14]、广义S变换(Generalized S-Transform, GST)[15,16]、分段改进S变换(Segmented Modified S-Transform, SMST)[17]、优化S变换(Optimized S-Transform, OST)[18]等。STFT通过引入一个与时间和频率相关的窗口函数获得时域特征，由海森堡测不准原理可知，固定窗函数不能同时获得理想时间分辨率和频率分辨率。因此，STFT不具有可变时频分辨率的特性，无法满足电能质量扰动特征精确提取的要求。WT被广泛应用于非平稳信号的分析。当使用小波变换或其扩展小波包变换时，需要选择不同的母小波和分解级别来检测信号的不同频率成分，这影响小波变换检测非平稳信号的适用性。对于扰动信号的时频特征提取，不仅需要准确反映出电压暂升、暂降、中断和闪变对基频幅值的影响，还需要准确检测出谐波和暂态振荡的频率成分。即大多数情况下，扰动检测需要在高频处有更好的频率分辨率，在基频处有更好的时间分辨率。ST可以看作STFT和小波变换的改进，利用高斯窗口来调整时频分辨率。但ST与实际需求相反，ST在高频段提供了更好的时间分辨率，在低频段提供了更好的频率分辨率，为了改善这种情况出现了以下几种改进ST。广义S变换在S变换的基础上增加调节因子，一定程度上提高了时频分辨率，但扰动信号频率跨度较大时依然无法满足不同频率点对时频分辨率的要求。SMST引入窗宽调节因子改进S变换，针对不同扰动信号分频段设置参数，一定程度上提高了时频分辨率，但参数跳变会导致不同频段之间出现过渡不平滑的现象，可能会对特征提取产生影响。OST同样引入调节因子对窗函数进行改进，同时提出能量集中度作为参数选取依据，时频分辨率相较于SMST进一步提升，但SMST与OST并没有从根本上解决基频幅值检测能力差的问题，并且二者窗口宽度依旧和频率呈反比关系，这会导致频率分辨率随频率增加而降低。

为了解决以上问题，本文提出一种基于最优Bohman窗的改进S变换(optimal Bohman window modified S-Transform, BST)，选用Bohman窗作为窗函数，通过直接控制窗长获得最优时频分辨率。对于基频，设计具有较窄时域宽度的窗口，其频谱具有较低的旁瓣，可以有效地减少频谱泄漏，有利于准确检测基频振幅；对于高频，设计具有较宽时域宽度的窗口，其频谱具有较窄的主瓣，可以获得较高的频率分辨率。Bohman窗的设计及其固有的最佳能量集中特性保证了BST在低频段具有更好的时间分辨率，能够检测基频振幅和发生时间的变化，在高频段具有更好的频率分辨率能够检测谐波和暂态振荡。同时加入动态测度快速算法将N点BST的计算复杂度[19]从O(N2log2N)降 到O(Nlog2N)，使该算法具有更好的实时性。仿真分析和实验结果表明本文所提算法能够实现对电能质量扰动信号时频特征的精确快速提取。

2 基于最优Bohman窗的改进S变换

2.1 S变换

作为时频分析方法的一种，S变换采用窗宽调节因子σ与信号频率f相关的高斯窗作为窗函数，连续时间信号x(t)的S变换定义为

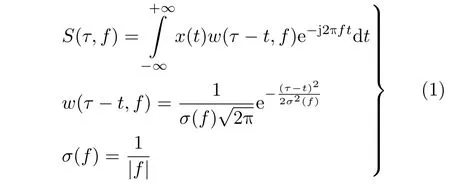
其中，t为时间，f为信号频率，τ为时移因子，控制窗函数在时间轴t上位置的参数，w(τ −t,f)为高斯窗函数，σ(f)为窗宽调节因子。

离散S变换可由快速傅里叶变换实现，令f →n/NT，τ→kT由式(1)可得S变换的离散形式为

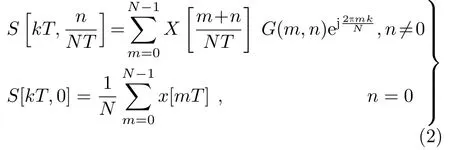
其中，N为采样点数，T为采样时间间隔，m,n,k的取值为0到N−1，G(m,n)为高斯窗函数的傅里叶频谱。

2.2 最优Bohman窗的改进S变换

Bohman窗可以通过调节其窗口长度控制窗口形状，即可以通过调节其长度参数实现对主瓣宽度和旁瓣幅值的控制，其函数表达式为

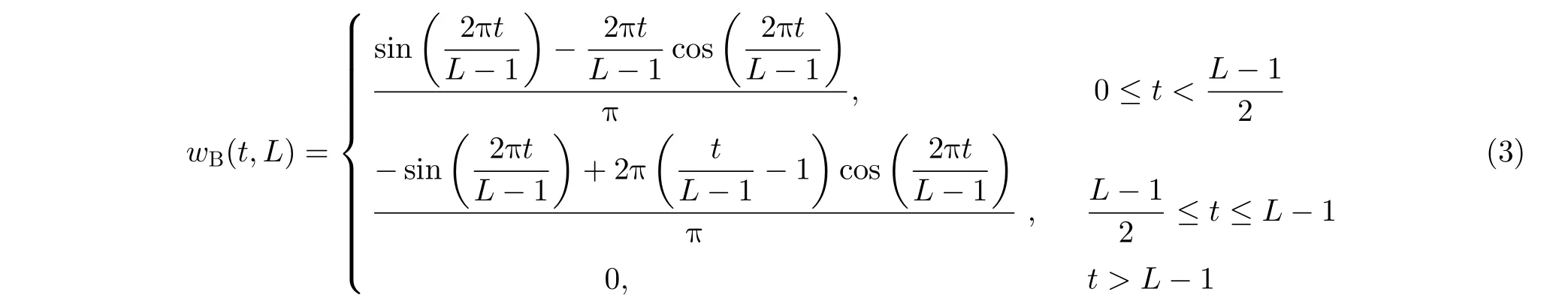
其中，L表示窗函数的窗口长度。不同长度参数L窗口形状不同，给出不同L值时Bohman窗的时频特性如图1所示。

由图1可知，窗口形状发生改变时Bohman窗的主瓣宽度和旁瓣幅值都会随着发生改变。L值越大时，主瓣越窄，旁瓣越低且旁瓣衰减速率越快，即时域分辨率变低，频域分辨率变高，因此窗口长度会影响特征提取的精度。

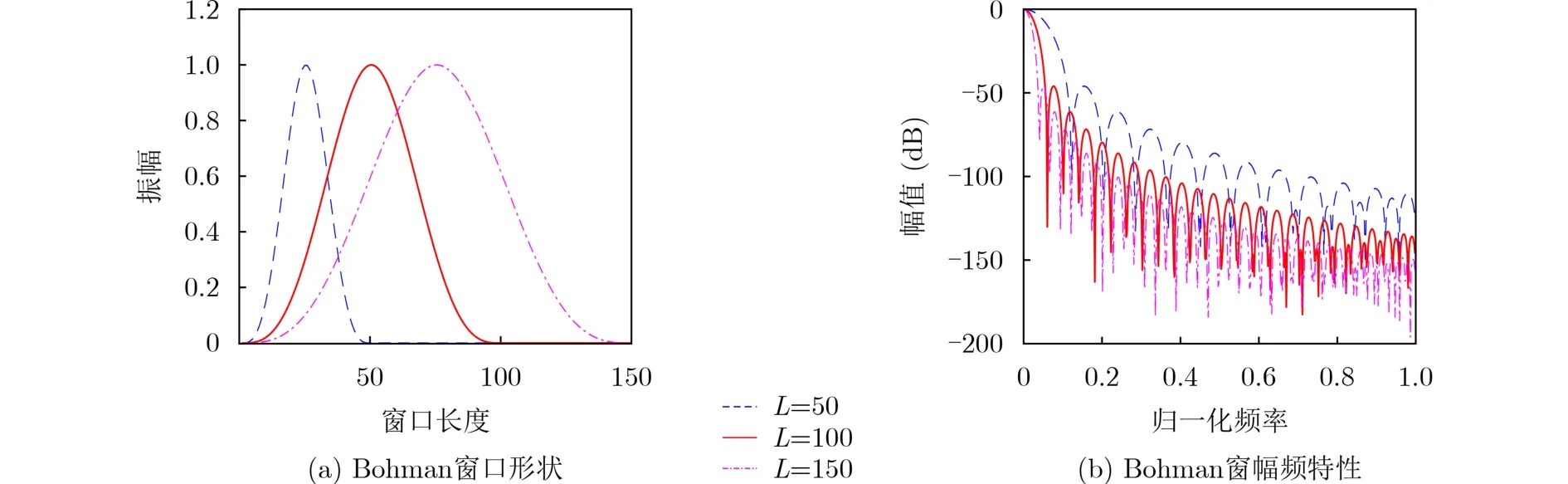
图1 不同L值Bohman窗时频特性

由式(1)可知高斯窗函数窗宽调节因子σ(f)取值由频率|f|决定，采样频率相同时，不同类型扰动信号在同一频率点的时频分辨率相同，且时频分辨率均随频率成反比变化趋势，这将无法满足不同扰动类型对时频分辨率的要求。由图1可知Bohman窗可以通过调节窗口长度控制时频分辨率，且其长度参数L与 频率|f|无关；从图2可以看出，控制窗口长度相同时，相较于高斯窗，Bohman窗主瓣更宽，旁瓣更低衰减速率也更快。因此本文提出一种直接控制窗函数窗口长度的改进S变换，其表达式为

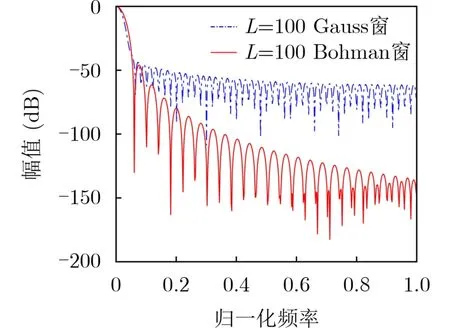
图2 相同L值时Bohman窗和Gauss窗幅频特性

其中，wB(τ −t,L)为Bohman窗函数的连续形式。

2.3 最优长度参数L值的选择

不同电能质量扰动信号对时频分辨率的要求不同，为了更好地提取扰动特征，将完整信号频段划分成两段，定义以电压中断、暂升、暂降、闪变为主的扰动信号在(0,100] Hz的低频段；以谐波、暂态振荡为主的扰动信号在(100,1600] Hz的高频段。

由2.2节可知，Bohman窗的长度参数L会 同时影响时域分辨率和频域分辨率。低频段，为了精确检测基频幅值的变化情况一般需要较高的时间分辨率，但时间分辨率过高又会使基频幅值曲线非扰动部分的平直度变差(选用标准差作为衡量平直度好坏的指标)，因此低频段最优长度参数L1的选择应该在保证一定时间分辨率的前提下让平直度尽量好。

通过以上分析，我们可以推断，留学生的语言能力与其语用语言能力有一定的关系，但与其社交语用能力之间关系不大。留学生的社交语用能力比其语用语言能力发展得要慢。这就要求我们在教学中加强对学生社交语用能力的培养。

以发生在0.14～0.17 s中断幅值为1 p.u.的电压中断信号为例，设置采样频率为3.2 kHz，采样点数为960。计算L取不同值时的BST模向量绘制出图3(a)的基频幅值曲线(50 Hz处BST模向量)，对其非扰动部分求标准差得到图3(b)所示的BST模向量平直度与L值关系图，由图3(b)知，L取96时标准差最小，因此低频部分最优长度参数L1为96。

图3(a)是几个典型L值对应的基频幅值曲线，从图3(a)可以看出L值越大BST模向量扰动部分幅值与实际理想值0的误差越大，其原因是L值越大，窗函数在频域主瓣越窄，因此时域分辨率变低，幅值检测能力也越来越弱。而当LL1时BST模向量非扰动部分出现了波动，是因为BST循环移位求快速傅里叶逆变换，相当于对原始信号乘上一个同频旋转因子，即

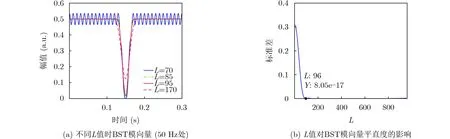
图3 L值对BST模向量的影响

由上可知采样频率fs1为 3.2 kHz时，L=96，对同一频率点而言，为保持时频分辨率不变[20]，采用其他采样频率fs2的L值由式(6)决定。

高频部分需要较好的频率分辨能力来识别谐波和暂态振荡信号的频率成分，与低频部分不同，高频部分最优长度参数的选取是通过实验测试得出的，当L2取346时能够获得较好的频率分辨率，如果采样频率发生改变，同样可以通过式(6)计算出最优长度参数L2。

3 动态测度FBST快速算法

已知N点信号的ST时间复杂度为O(N2log2N)，随着采样点数N的增大会导致计算量剧增，可能会使ST的运行时间无法满足实时分析信号的要求[21]。实际分析过程中S变换时频矩阵中大多数行对于扰动信号的频谱分析并没有帮助，这样不仅增加了计算量还影响了算法的实时性。因此如何去除非主要频率点所在行，保留主要频率点所在行是实现快速算法的关键。据此，本文采用基于极大值包络的动态测度[22]检测主要频率成分实现BST的快速计算(Fast optimal Bohman window modified S-Transform, FBST)。

以信噪比为30 dB的暂降+谐波+暂态振荡信号为例，图4中蓝线是复合扰动信号进行傅里叶变换后得到的频谱图。由图4可知，5, 7次谐波和暂态振荡这些主要频率点对应幅值较大采用设定阈值的方法很容易去除周围的非主要频率点，但基频附近会存在很多由电压暂降幅值突变导致的幅值大于3次谐波幅值的频率点，此时如果再采用阈值的方法，基频附近的非主要频率点将会被误判为主要频率点。仔细观察可以发现基频附近极大值点沿频率变化方向呈下降趋势，此时采用动态测度[23]算法即可筛选出3次谐波对应频率点。图5为图4中频谱极大值包络极大点的动态测度图，从图中可以看出基频附近虽然存在幅值大于3次谐波幅值的频率点，但其动态测度很小；其它主要频率点的动态测度更是明显大于周围非主要频率点的动态测度，此时通过设置合适的阈值即可筛选出主要频率点m。

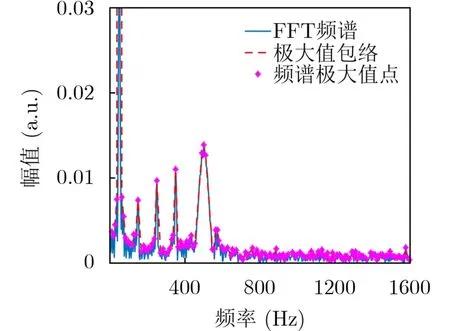
图4 频谱极大值包络

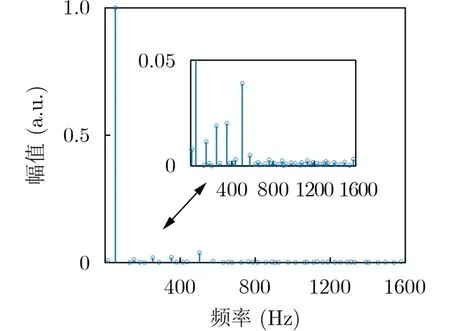
图5 极大值包络的动态测度

表1 计算量和时间复杂度对比

4 仿真实验与分析

用MATLAB仿真生成时域扰动信号和频域扰动信号进行仿真实验，其中时域扰动包括暂升、暂降、中断、闪变；频域扰动包括谐波、暂态振荡，为验证FBST的有效性，控制实验条件完全相同的情况下和SMST, OST进行对比，设置采样频率为3.2 kHz，采样点数为960。

4.1 时域特征对比

图6(a)、图6(b)为发生在0.135～0.175 s扰动幅值为1.5 a.u.和0.6 a.u.的电压暂升和暂降信号；图6(c)为发生在0.13～0.17 s扰动幅值为1 a.u.的电压中断信号；图6(d)为闪变频率为20 Hz和闪变幅值为0.2 a.u.的电压闪变信号，及相应SMST, OST, FBST的幅值检测结果。从图6可以看出不同扰动信号下FBST跟踪电压波动的能力均为最强，因此相较于其它两种算法FBST时域分辨率更高更能反映实际扰动发生的情况。表2为上述扰动信号完成计算所需时间，FBST的计算时间均在10 ms以内，因此相较于其它两种算法FBST具有更好的实时性。

表2 时域扰动计算时间对比(ms)

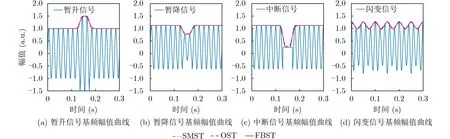
图6 不同信号基频幅值曲线

为了进一步对比各算法的基频幅值检测能力设置更短的扰动时间0.03 s, 0.02 s, 0.01 s，并以相对幅值误差作为衡量检测能力的标准(相对幅值误差为S变换得到的扰动幅值和扰动理论幅值差的绝对值)，从图7可以看出当扰动信号持续1.5个周期时FBST暂降和中断的误差接近为0，暂升的误差也小于SMST和OST；当扰动持续时间变短至0.5个周期时，FBST的相对幅值误差对比SMST和OST仍更小。因此FBST在扰动时域特征分析中更具优势。

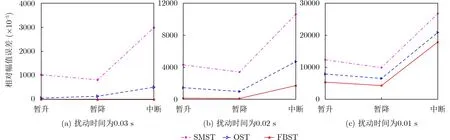
图7 不同扰动时间下的相对幅值误差

4.2 频域特征对比

如图8所示，谐波包含3～29次的奇次谐波，其中3, 5, 7次谐波随机生成0.1～0.2的幅值，9～29次谐波设定在幅值较小的0.01～0.05区间并且随机生成。暂态振荡幅值设为0.04，持续时间为2.5个周期。

图8 谐波和暂态振荡高频部分频率幅值曲线

表3为谐波和暂态振荡信号的相对幅值、频率误差(相对频率误差为S变换得到的扰动频率和理论扰动频率差的绝对值)。结合对应图表可以看出，尽管3种算法均能识别出暂态振荡频率成分但FBST的频率分辨率最高；分析谐波信号时FBST的精确度均高于SMST和OST，各次谐波的幅值、频率相对误差均为0。SMST在分析第9次谐波时开始出现幅值误差，之后整体误差仍呈不断增大的趋势；在分析第15次谐波时开始出现频率误差，之后还多次出现无法识别主要频率点的情况，原因是SMST频率分辨率太低不足以满足高频扰动对频率分辨率的要求，另外这些高次谐波的幅值较小所以其特征容易受到相邻谐波的影响。OST幅值、频率误差相比于SMST要好很多，但仍存在幅值、频率误差，而FBST采用直接控制窗长的方式并不受频率的影响，在分析高次谐波时仍能保持较高的频率分辨率进而实现对高次谐波特征的精确提取。表4为处理上述扰动信号完成计算所需时间，FBST相较于其他两种算法所需时间更短，实时性更好。

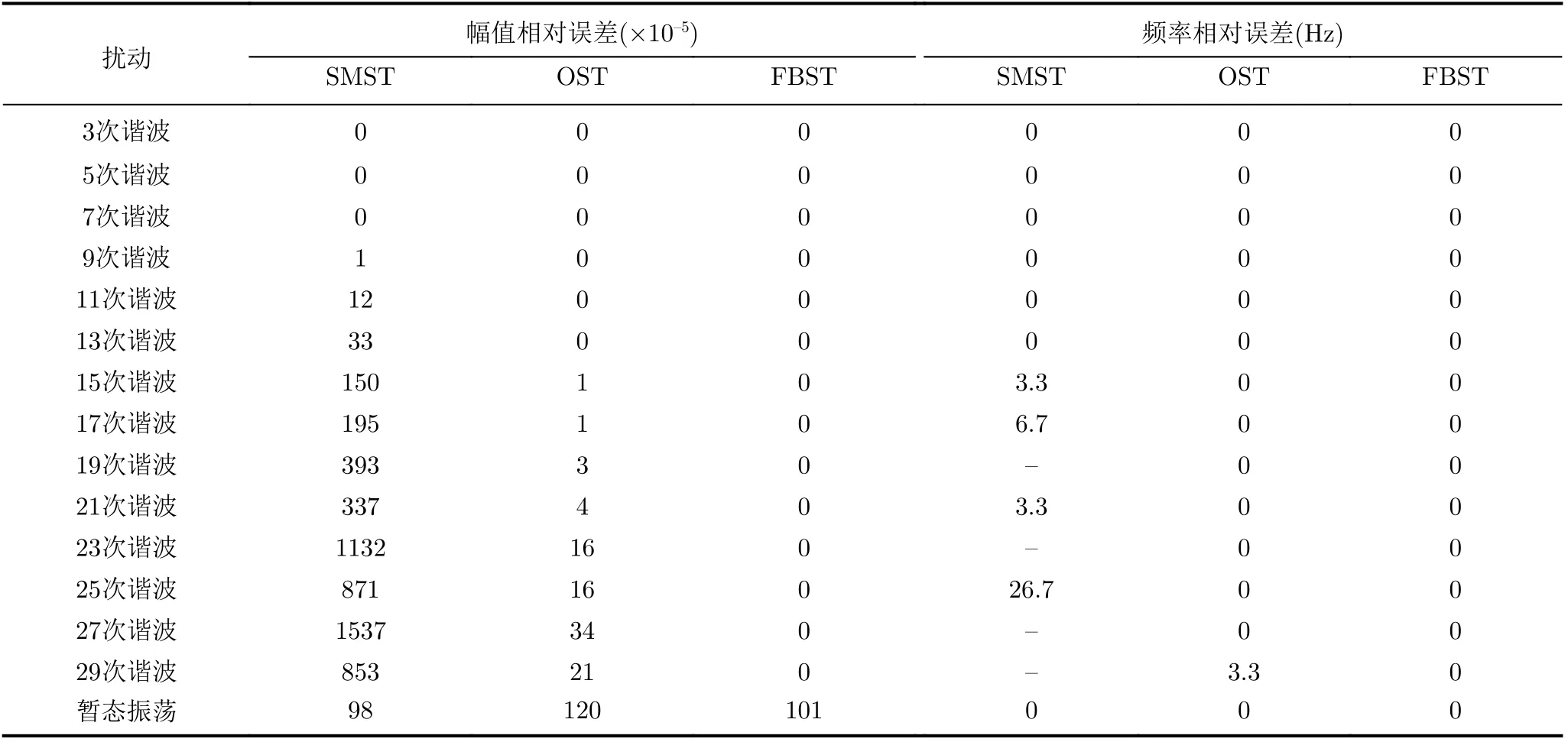
表3 谐波与暂态振荡信号相对误差对比

表4 频域扰动计算时间对比(ms)

5 实验验证与分析

5.1 Simulink仿真实验

利用Simulink搭建线路故障模型1，模拟图9(a)中两相短路故障引起的电压中断、暂升和暂降。该模型主要包括1个3相电源(11 kV, 30 MVA)，两个放置在11 kV总线处模拟A、B两相接地短路的线路故障模块，1个变压器和1个RLC负载。设置3相电源中性点不接地，线路故障1和线路故障2模块开关时间分别是[0.1,0.15]和[0.15,0.21]，故障电阻RON分别是5 Ω和0.1 Ω，接地电阻Rg， 缓冲电阻Rs，缓冲电容Cs均设置为0.01 Ω, 106Ω, ∞ F。

给出线路故障引起的变压器1次侧3相电压波形如图9(b)所示，其中A和B相电压波形为先暂降后中断扰动信号，C相为暂升扰动信号。因A, B扰动相似，选择A相电压波形进行分析，不同算法对A,C相电压基频幅值检测结果如图10所示，从图10可以看出本文所提算法能够更好地跟踪线路故障引起的电压波动，因此幅值检测也更准确。

图9 电压扰动Simulink模型

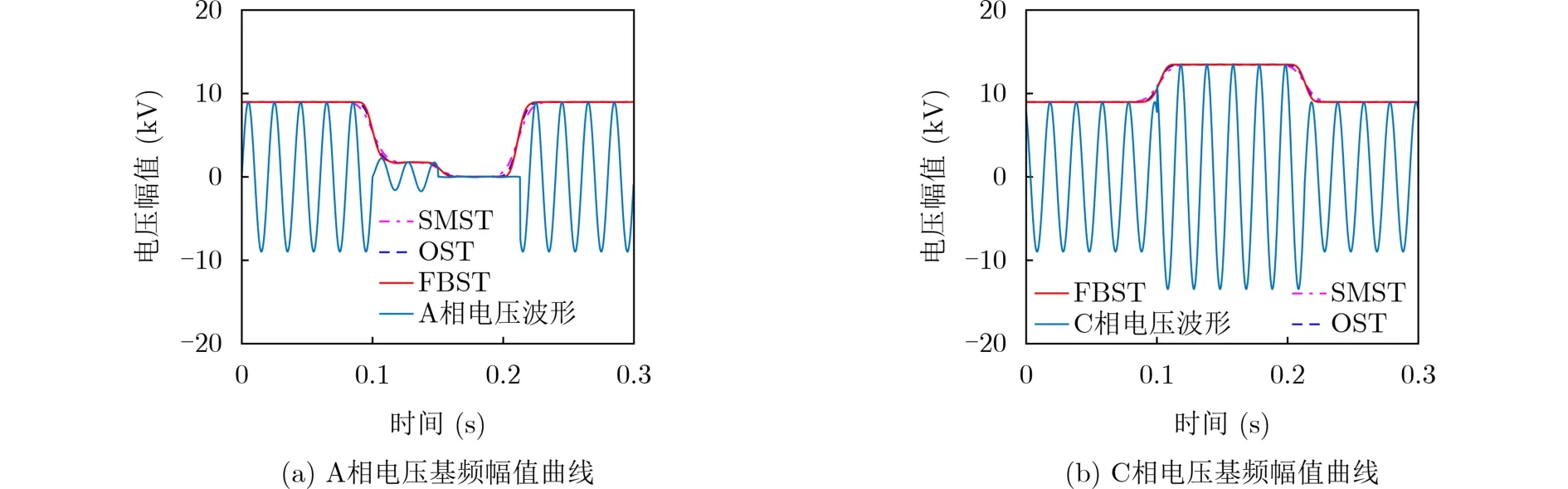
图10 不同算法下基频幅值曲线

利用Simulink搭建线路故障模型2，模拟图11(a)中非线性负载投入引起母线电流出现谐波。该模型主要包括1个3相电源(11 kV 30 MVA)，1个变压器和放置在0.4 kV总线处的非线性负载模块，该模块包括不可控整流桥和RL负载。设置3相电源中性点内部接地，不可控整流桥导通电阻RON，缓冲电阻Rs，缓冲电容Cs设置为10–3Ω, 105Ω, ∞ F，电感L和 电阻R设置为0.5×10–8H, 18 Ω。

给出线路故障引起的变压器1次侧3相电流波形如图11(b)所示，A, B, C 3相均为谐波电流信号。选择A相电流波形进行分析，不同算法的电流频率幅值曲线如图12所示，由图12可见SMST与OST无法准确检测出幅值较小和频率较高的谐波成分，但本文所提算法在此场景下依然能够准确检测出各次谐波成分，因此频域检测能力更强。

图11 电流扰动Simulink模型

图12 A相电流频率幅值曲线

5.2 实测实验

为进一步验证本文所提出算法的实际应用效果，搭建电能质量扰动信号检测平台对算法性能进行测试，测试平台结构如图13所示。将搭建好的Simulink标准信号电路模型通过StarSim软件载入实时仿真器(MT 3200 HIL)产生电能质量扰动信号；通过数据采集装置中的A/D转换器对扰动信号进行采样；利用DSP(TMS230F28335)对采集到的数据进行降采样；将采样处理后的数据传输至上位机进行时频特征提取。

图13 电能质量扰动信号检测平台

本文对9种电压扰动信号进行实际测试分析，测得3种算法的幅值相对误差如表5所示，实际测试误差要比仿真分析误差更大，这是由于信号处理设备和传输通道引入的噪声，即便如此，本文所提算法的误差整体仍较小；测得3种算法所需运算时间如图14所示，本文算法完成特征提取平均时间为8.7 ms远小于300 ms，因此本文算法能更好地满足实际场景下精确快速提取扰动特征的要求。

图14 不同算法所需运算时间

表5 实测信号相对幅值误差(10–5)

6 结束语

本文提出了一种基于最优Bohman窗的改进S变换电能质量扰动特征提取方法。通过直接控制窗口长度的方式，让Bohman窗在低频段有一个较宽的主瓣使FBST具有较好的时间分辨率来检测基频幅值的变化；在高频段有一个较窄的主瓣使FBST具有较好的频率分辨率来检测扰动信号的频率成分。使用基于极大值包络的动态测度快速算法准确筛选出主要频率点减少计算量。仿真分析和实测实验结果表明，相较于SMST，OST本文所提算法在提取各类扰动信号特征时误差整体较小；同时本文所提算法所需时间最短且均小于15 ms，因此能够实现电力系统中常见扰动信号特征的精确快速提取。