联通经验 关注发展——对“用数对确定位置”教学的若干思考

□ 章 颖

《义务教育数学课程标准（2022 年版）》在“空间与图形”的第三学段（5～6年级）中指出：“能用有序数对（限于自然数）表示点的位置，理解有序数对与方格纸上点的对应关系。”在日常生活中确定位置有多种途径和方式，而在数学学习中一般用数对来确定位置，那如何让学生感受到用数对确定位置的必要性和简洁性？在日常生活中确定位置往往没有“原点”的概念，那又如何让学生感受到“原点”作为数对核心要素之一的必要性？

基于上述思考，以人教版教材五年级上册“用数对确定位置”为例，从现实生活中的情境引出用数对确定位置，让学生体会数对与平面上点的一一对应关系，初步感知平面直角坐标系的表示方法以及思想，初步感受这种表示方法带来的便利，促进学生高阶思维的发展。

一、通过冲突与碰撞，感受数对产生的必要性

如何确定数对中两个数的位置，用怎样的方式描写数对，每个学生都有独特的理解，教学时可以利用学生的思维碰撞，感受数对产生的必要性，减少生活中“先行后列”的方法带来的负迁移。

【教学片段1】

师（出示图1）：张亮同学举手提问，你能帮老师找到他坐在哪里吗？

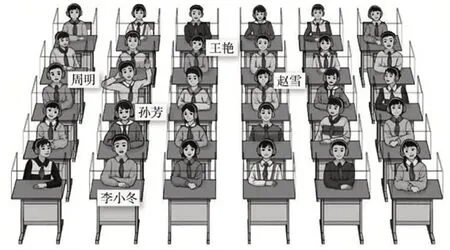
图1

（根据学生的回答，教师板书：

师：这么多方法中，你喜欢用哪种方法？请说说理由。

生：我喜欢“→2↑3”，因为它能看出是先从左往右数，再从前往后数。

生：我喜欢“3，2”“2，3”，因为它们很方便，很简明。

生：我觉得“××的××边”不好，因为有时一个人的某一边会有很多其他同学。

师：同学们很会思考，为了记录的统一，数学上规定，先竖着看在第几列，再横着看在第几行，记作（2，3）。

学生通过交流，发现同一位置有多种表述，如果没有统一的标准，不利于人们之间的交流，从而感受数对产生的必要性及其简洁性。

二、通过抽象与对比，感受确定原点的重要性

“用数对确定位置”是用有序数对来刻画二维空间中某一点的位置，即在平面直角坐标系中研究点的位置是如何用数对来刻画的。虽然小学阶段所用的是“方格纸”坐标系，但它也是真正坐标系的雏形。因此它必须要具备坐标系的三个关键要素：原点、方向、单位长度。在唯一确定的直角坐标系中，每个有序数对与平面上的每个点会建立一一对应关系。在教学中教师可以创设直角坐标系与实际情境图的对比，让学生感受三要素的重要性和便捷性，通过对比，让学生的认知水平从原有的一维数轴拓展到二维平面直角坐标系。

【教学片段2】

师：现在我们把张亮的位置抽象成一个点，把它标记在方格纸中。你觉得它的位置怎样表示比较合适？

生:（2，3）。

师：2和3分别表示什么意思呢？

生：2 表示从左往右数第2 列，3 表示从下往上数第3个。

师：我们把第一行都放在横轴上，第一列都放在纵轴上，你能把横轴和纵轴的数字补充完整吗？（根据学生的补充将横轴、纵轴补完整，如图2）

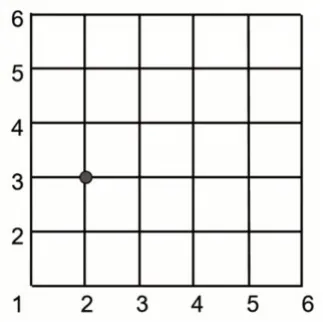
图2

师：横轴和纵轴都是从1开始的。你还记得数轴是从几开始计数的吗？

生：从0开始。

师：那横轴、纵轴是从0 开始计数好，还是从1开始计数好？

生：我觉得从1 开始就可以，因为生活中的座位都是从1 开始计数的，电影院也是从1 排1 号开始的。

生：我觉得从0开始计数好，因为如果1组1号向教室门的方向走，那他的位置就是零点几了，从1开始没法表示。

生：我觉得也是从0开始计数好，和数轴统一。

生：我也赞同从0 开始计数，你看地球仪上有经线和纬线，有时就有零点几度，如果从1 开始计数那就表示不出来了。

师：的确，生活中有很多情况都是从0开始的，比如航海时的位置、在地图上确定位置等。教室的座位图我们也可以从0开始计数。如果从0开始计数，你觉得哪里代表0比较合适？

生：前门进来要空一些位置才开始摆课桌椅，所以0和1之间的距离正好是教室走廊这边的墙和课桌之间的距离。

师：好，那我们就根据大家的建议，把这幅图补充完整。这幅图现在就和以前学习的数轴统一起来了，我们把横轴和纵轴的交叉点（0，0）叫作原点（如图3）。

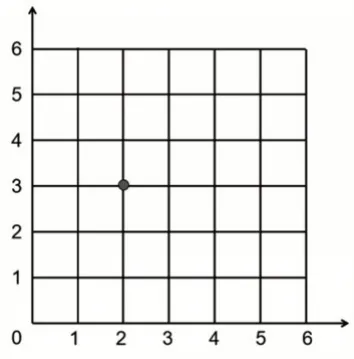
图3

在学生建构直角坐标系的过程中，自然引出横轴、纵轴、原点这些基本要素，使学生在潜移默化中感悟了坐标系的思想。“用数对确定位置”不是单纯地在生活中确定位置，而是为认识直角坐标系奠定基础。因此，教师可以舍去用数对表示“块”的内容，直接从“情境图”抽象到“格点图”，再从“格点图”抽象到“坐标系”。在这一过程中，通过形来研究数的特点，通过数来呈现物体的位置，在用方格纸和数对表示点的位置这两种方法之间架起数与形的桥梁，让学生了解数对与方格纸上的点存在一一对应关系。

三、通过探究与感悟，感受数形结合的直观性

在方格纸中找到数对相应点的位置，对学生来说不难掌握，那么为什么要建立数对与方格纸上的点之间的关联呢？其深层次的目的是让学生直观地理解直角坐标系，在学习有序数对的过程中为进一步学习平面直角坐标系做好铺垫，为日后研究解析几何奠定基础。

【教学片段3】

教师出示数对（6,3）、（5,5）、（3,4）、（1,3）、（3,3）、（3,2）。

师：这里有一些数对，你们能很快找出它们的位置吗？

师：哪些点在同一条直线上呢？

生：我发现（6,3）、（1,3）、（3,3）都在第3行（如图4）。

图4

生：我发现（3,4）、（3,3）、（3,2）也在同一条直线上，只不过它们都在同一列，它们都在第3列上（如图5）。

图5

师：如果连接（5,5）和（3,3）会得到怎样的线段？

生：一条斜线（如图6）。

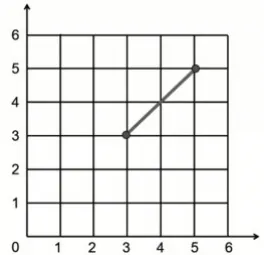
图6

师：这条斜线有什么特征？

生：如果延伸的话，这条直线刚好是从原点（0,0）出发的，而且线上每个数对的两个数字都相等，比如（2,2）、（4，4），等等。

生：我能用一个数对把它们都表示出来，就是（x，x），只要数对中的两个数是一样的，这个数对上的点就一定在这条斜线上。

通过这样的活动，学生很自然地感受到点的连线是变化多端的，每一个点都对应一个数对，它们之间是一一对应的，同时通过点所表示的线段，体会数对中行、列的变化与图形变化之间的紧密联系。用有序数对所对应的点组成图形，其实质是用“数”来描述“形”，通过“数”与“数”之间的连接，画出各种方向的直线，这充分体现了数形结合的直观性。

四、通过联系与对比，感受直角坐标系应用的广泛性

直角坐标系在小学阶段应用广泛，如在图形变换、函数思想、行程问题等领域经常出现。因此，可以在练习中加入与这些领域有关联的元素，既丰富练习的形式，又增强练习的层次，还有助于培养学生的高阶思维，让学生感受数学知识的内在联系。

【教学片段4】

教师出示练习1（如图7），让学生独立完成。

图7

师生校对第（1）题和第（2）题的答案。

师：谁来说说你有什么发现？

生：我发现三角形ABC和三角形HIG的形状、方向都一样，只是位置变化了。

生：我发现三角形ABC和三角形HIG每个顶点用数对表示时，第1 个数发生了变化，第2 个数都一样。

生：对的。数对中第1个数表示的是横轴上的位置，它变了，表示在横轴上发生了移动；而第2个数表示的是纵轴上的位置，它没变，说明这个图形只是平移了。

师：同学们真会观察，我们发现把一个图形连续翻转两次相当于把这个图形进行平移，图形的大小、形状都没有改变，只是位置发生了改变。

小学阶段图形变换主要有三种方式：平移、旋转和轴对称。这三种变换方式之间有着密切的联系，将这种联系放在直角坐标系中就显得直观可视。因此，这一环节通过先让学生画轴对称图形，再引导他们观察、思考数对的变化，使学生更容易理解翻转与平移的关系。

数对除了能帮助学生发现图形变换之间的关系，当把数对放入直角坐标系时，还能帮助学生直观形象地了解一些基本的函数知识，发现函数中蕴藏着的变与不变。

【教学片段5】

教师出示练习2（如图8），让学生独立完成。

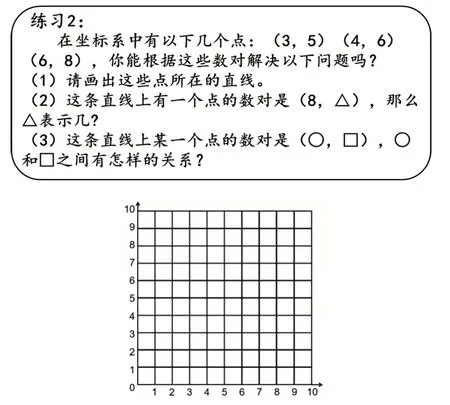
图8

师生校对第（1）和第（2）题的答案。

师：谁能来说说第（3）题中○和□有怎样的关系？

生：我发现题目中每个数对的第2个数都比第1个数大2，也就是□=○+2。

生：我觉得还可以倒过来说，○=□-2。

生：其实就是这个点的数对，纵轴上的数比横轴上的数大2。

师：看来数对还能表示直线上任意一点的变化。

这一环节通过逐个确定点的数对，促使学生在确定数对的过程中探索出变量之间的变化规律，体会变量中蕴藏着的关系，初步感悟函数思想。

总之，在教学过程中，教师自身要深入理解数对的本质含义，引导学生用数对的变化认识图形的变化，帮助学生感悟通过几何建立直观表象、通过代数得到数学表达的过程；引导学生用数对解决平面直角坐标系中的问题，帮助学生感悟坐标系是联系代数与几何的桥梁，理解坐标系中的数对与平面上的点一一对应的关系；引导学生用数对解决现实问题，帮助学生感悟数形结合的精妙，提升学生的空间观念和几何直观。