整体把握 让运算教学走向结构化
——除数是两位数的除法“调商”教学实录与评析
2022-11-29凌璐予执教徐丹红评析
□ 凌璐予 执教 徐丹红 评析
【教学内容】人教版教材四年级上册第76~77页《笔算除数》例3、例4。
【教学目标】
1.结合具体情境,让学生经历除数是两位数的除法的调商过程,进一步掌握调商方法,能正确进行笔算。
2.在交流分享中理解调商(商偏大要调小、商偏小要调大)的道理。
3.体会运算意义在运算中的作用,培养学生自主解决问题的能力。
【教学重点】掌握调商方法,能正确进行笔算。
【教学难点】理解调商的道理。
【教学过程】
一、情境引入,整体呈现
师:“双十一”快到了,老师想在淘宝上给同学们买些奖品,看看老师的购物车里都放了什么?
(课件出示图1)

图1
师:老师想用200 元买其中一样奖品,大约能买几个?
(学生估计结果:小风扇大约6 个,小音响4~5个,小夜灯6~9个)
师:那实际到底能买几个呢?可以怎么办?
生:算一算。
(学生先口答列出算式后,再说说200÷31的笔算过程,教师依据学生的回答板书)
(评析:课始,教师创设了购物的情境,借助问题“实际到底能买几个?”引入,然后同时呈现初商正好、偏大、偏小的三道除法算式,让学生通过估一估的方法,对三道算式的商形成整体感知——单价越低,购买数量越多,以此培养学生的数感。)
二、自主探究,交流算法
(一)探究“四舍”——呈现作品,暴露思维
师:小音响到底能买几个呢?请大家自己算一算。
(学生在学习材料单上独立计算200÷43,教师巡视、收集学生的不同写法,并逐一展示,如图2)

图2
师:老师收集了三个同学的写法,你能看懂谁的?我们先一起看①号作品,这个同学列了2个竖式,你们能看懂吗?这是什么意思?
生:第一个竖式是把43 看作40,用5 来试商,发现200 不够减;第二个竖式是用4 来试商,结果余28。
师:你们同意这么改吗?说说你的理由。
生:5乘43是215,可是一共只有200,不够减。
师:原来215比200大,钱不够付了,这说明什么?
生:商太大了,需要把商调小。
师:我们再来看看②号作品,谁看懂了?
生:他是先用5来试商,发现乘出来的积比200大,所以就把5改成了4,结果余28。
师:采访一下这个同学,你是这样想的吗?(学生点头)你怎么没算出来就发现商偏大?
生:因为 40 乘 5 已经是 200 了,所以 43 乘 5 肯定超过200,一定不够减。
师:原来你是用估算判断的,为你的智慧点赞。再看③号作品,他是直接写商4,那么他又是怎么想的呢?我们请他来介绍一下。
生:我是这样想的,先把43估成40,200里面有5个40,但我们把除数估小了才是40,而乘积比200大,所以要把商5减小1,变成4。
师:看来,这三种写法的思考过程是一样的,都是用四舍五入法试商,发现商5 偏大,需要把商调小。虽然三个人的记录方法不一样,但结果都是4余28。
(评析:除数是两位数的除法,怎样调商是学习的难点。教师呈现了学生的不同写法,其意图是让不同学生的思考留痕,让调商的过程留痕。从学生有痕的作品中可以看出,学生发现215比200大,减不了,这说明商偏大需要调小。教师顺着学生的发现,围绕核心问题“商5 为什么要改成商4”展开讨论,以帮助学生掌握算法。教师通过采访第2 个用估算判断不够减的学生,引导学生灵活选择方法来判断商是否合适,以培养学生的数感,提高学生的运算能力。)
(二)探究“五入”——比对写法,发现共性
师:最后我们来算算200 元能买几个小夜灯,请大家用自己喜欢的方法记录。
(教师巡视、收集学生的不同写法,并同屏展示,如图3)
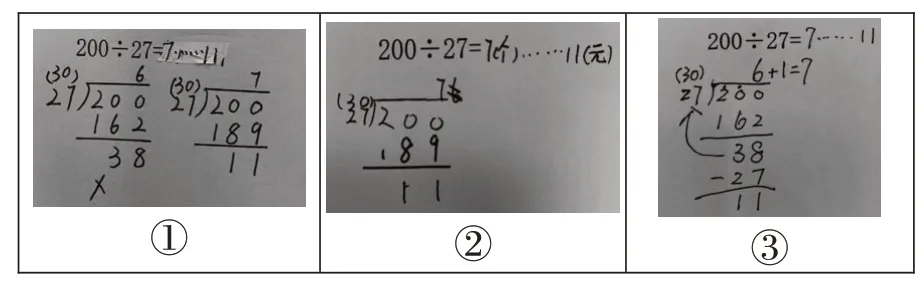
图3
师:这三个同学的结果都是7余11。仔细观察这三种写法的思考过程,大家有没有什么发现?跟你的同桌交流一下。
(同桌之间交流想法)
师:谁来分享一下你的发现。
生:三种写法都是先试商6,后来调商为7。
生:第①种第一个竖式试商6,第二个竖式调商为7。
生:第②种是直接在商那里把6调为7。
生:第③种写了6+1=7,也是把6调为7。
师:是呀,三种写法都把商调大了,那为什么要调大呢?
生:因为不改的话,余数是38,就比除数大了。
师:余数比除数大,说明我们一开始试商偏小了,需要把商调大。那么你们把商调大了多少?
生:调大1。
师:为什么调大1呢?
生:因为38里只能再分一个27。
师:余数不仅告诉我们商偏小了,还告诉我们商偏小了1。我们发现余数38 里还能再买一个小夜灯,买一个后还剩多少钱?找一找,几号写法把这个过程也表示出来了?
生:第③种,38减27,还剩11元。
师:看来,这三种写法的思考过程也是一样的,都是先用四舍五入法试商,然后发现余数比除数大,也就是商偏小了,需要调大。
(评析:通过三种写法的对比观察,聚焦共同点“商6 调为商7”进行原因剖析。当余数比除数大时,说明商偏小,得出调商方法——调大。师生从三种不同写法中提炼出相同的思考过程,从而驱动学生寻找调商的方法,掌握算法。教师在引导学生掌握算法的基础上,还提高了他们灵活选择算法的能力。)
(三)对比观察——沟通联系,理解本质
师(出示图4):请大家仔细观察今天学习的这三道除法竖式,它们有什么共同点和不同点?
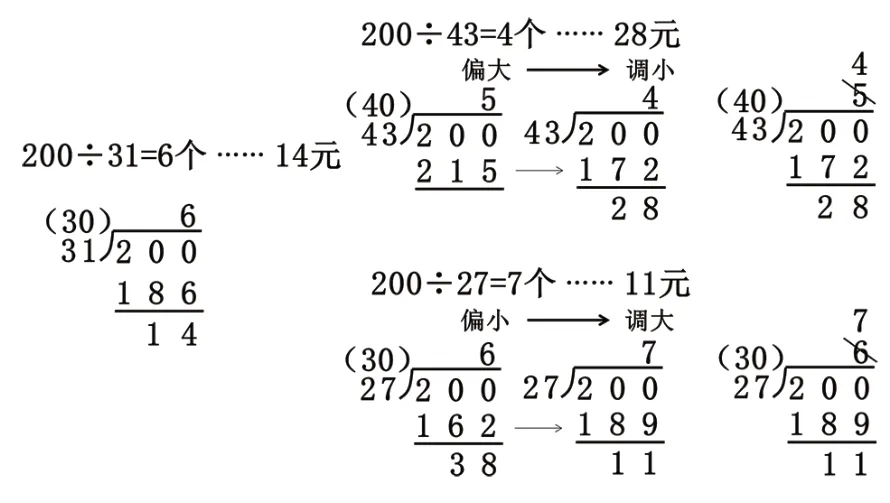
图4
生:除数都是两位数。(教师揭示课题:除数是两位数的除法)
生:它们都是用四舍五入法试商。
生:第一题不用调商,第二题和第三题都需要调商。
师:是的,用四舍五入法试商,有时候商正好,有时候商偏大或偏小,需要调大或调小,这个过程就叫作调商。
(评析:教师让学生进一步对比观察三道除法的计算过程,让他们形成对调商的整体认知,即在用四舍五入法试商时,有时不需要调商,有时需要调商。教师借助结构化的板书,帮助学生建构除数是两位数除法的知识网络,既指向内容,又指向方法及本质。)
三、进阶练习,内化提升
(一)基础练习
课件出示题目。
124÷21 96÷18 171÷19
学生独立完成后,师生共同校对答案。(教学过程略)
(二)辨析练习
课件出示题目。
根据试商情况,想一想需不需要调商。

学生独立完成后,师生共同校对答案。(教学过程略)
(三)拓展练习
课件出示题目。
观察下面的计算过程,你知道除数是几吗?
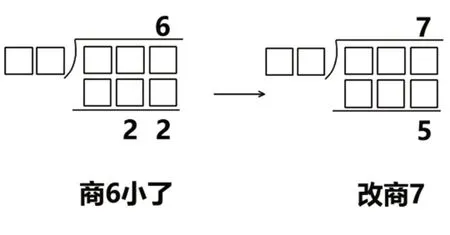
师:我们一起来挑战计算小超人,请你静静思考。
师:除数是几?
生:17。
师:那么多空格,你怎么知道除数是17的。你是怎么想的?
生:商7比商6大1,所以从余数里减掉了一个除数,还剩5,因此减掉的除数就是22-5=17,除数是17。
(评析:这是一道指向理解算理的推算题,在被除数和除数都未知的情况下,让学生通过商和余数的关系来推算除数。这一过程不仅让学生进一步理解了商和余数的关系,也发展了学生的推理能力。)
四、全课总结,交流感受
师:大家今天有什么收获?
生:学会了除数是两位数的除法。
生:学会了调商。
师:怎么调商?
生:当商偏小时要调大,当商偏大时要调小。
师:其实调商还有很多的小技巧呢,让我们在以后的学习中去慢慢感受。
【总评】
本课在单元整体教学的视角下,力求整体把握除数是两位数除法的笔算,让算法走向结构化。
一、整合内容,借结构化打破思维定式
除数是两位数的除法,调商是学习难点。教材用“四舍”法、“五入”法分成2 道例题进行教学,其优点是帮助学生学得扎实,弊端是学生在学完“四舍法”后容易机械地将商调小,学完“五入”法后机械地将商调大,形成思维定式,缺乏主动思考的习惯。因此,教师用“四舍五入”法整合教学,这样的结构化教学能让数学知识具有整体性,让学生在不同题型的变化中感悟方法,从而达到融会贯通、触类旁通的目的。
二、横向对比,借求同感悟算法本质
本节课安排了三个层次的对比:一是引导对比,在解决“200÷43”时,在交流三种方法的思考过程中,引导学生进行对比,发现都是商5 调为商4;二是自主对比,通过让学生同屏观察“200÷27”的三种不同写法,自主进行对比,发现共同点“都是商6改商7”;三是整体对比,对试商中正好、偏大、偏小三种情况的调商过程进行对比,在求同中发现算法的本质。
三、立体生长,借巧妙设计驱动灵活算法
运算教学的目标不仅要根据运算法则和运算律进行正确运算,还应在理解算理、掌握算法的基础上,促进学生选择合理的运算策略解决问题。本节课从两方面体现了这一目标:一是在交流过程中渗透选择运算策略,如在师生交流“200÷43”的环节中,利用呈现不同方法的学生作品,引导学生灵活选择精算或估算判断商偏大;二是在拓展练习中选择合理的运算策略,如在竖式中缺少数据的情况下,运用调商的原理来解决问题,进而深化对计算方法的理解。
总之,无论是理解算理,还是掌握算法,教师都应立足整体,引导学生将已有知识与所学知识进行同化,在知识融合的过程中实现认知结构的自主重构,使运算教学走向结构化。
