入湖三角洲水道结构对流量的随机响应试验研究
2022-11-29徐海珏宋晓龙白玉川
徐海珏,宋晓龙,白玉川
入湖三角洲水道结构对流量的随机响应试验研究
徐海珏1, 2,宋晓龙1, 2,白玉川1, 2
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300350;2. 天津大学河流海岸工程泥沙研究所,天津 300350)
在温和的外部环境条件下,入湖三角洲的形态演变过程始终表现出一定的随机特性,这给河-湖区域环境监测和水资源管理带来较大的不确定性.本研究在传统确定性的调查方法基础上,通过设置两种不同量级流量条件并分别重复两次的物理模型试验,进行了入湖三角洲水道结构对流量的确定性和非确定性响应规律研究.对准周期相似的三角洲水道的几何特征进行定性观察及其波动变化进行定量统计,一方面,确定性地揭示出随流量的变化,主流水道长度指标与它的正相关性,和三角洲中游各阶汊道分汊位置指标的波动特征、高阶汊道各项几何特征指标的平均波动周期的与它的非正相关性;另一方面,非确定性地分别揭示出低流量条件下三角洲上游分汊位置指标和汊道长度指标的平均波动周期与其均值的正相关性和负相关性.本研究提升了对三角洲水道分汊不确定性规律的认识,并为三角洲形态发展的随机模拟研究奠定了基础.
入湖三角洲;流量;水道结构;确定性与非确定性;物理模型试验
在上游水流与受水盆地的复杂相互作用下,入湖三角洲逐渐形成以分散的多尺度水道与泥沙堆积体为主要构成的地貌形态.在我国,入湖三角洲的形成和发展过程是冲积河流体系研究的重要组成部分,其中最著名的包括洞庭湖三角洲和鄱阳湖三角洲[1].以赣江为例,2020年,面对严峻的洪涝形势,对鄱阳湖区域入湖三角洲水道系统演化特征更高层次的认识变得更加迫切.在科学意义上,三角洲水道的确定性发展规律已受到相当多的关注,但对其随机演变过程中的自组织特性的研究仍然不足.特别是,这一问题已在实际的环境保护和防洪工程中凸显出来.
外部扰动对天然河流-三角洲的重要影响已出现在前人大量的研究中[2-4],但还不足以揭示三角洲形态发展的内部机制细节[5].一些对三角洲形态自组织机制的数值研究,发现了系统散乱分汊[6]和周期性淤积与下切[7-8]的复杂驱动模式,然而其忽略了一些代表性的自然影响因子.而且,由于一些测量技术上的限制,如分离内-外扰动的不同影响、实时观测野外三角洲的特征变化等困难,使得在人工控制的水沙环境条件下,物理模型试验成为研究三角洲自组织特性最现实、最有价值的技术手段.许多成功的物理模型研究提供了各种三角洲形态的动态特征信息,讨论了外部水沙输入与三角洲沉积构造之间的确定性关系[5, 9-12].在温和的环境控制条件下,这些试验结果能够展示出水道从“片流”向“渠道流”转换过程中的结构不确定性特征,证实结构以“临界比降”的出现为标志、开始侵蚀-沉积自循环过程对上游水沙输入条件的强依赖性等特质.
然而,很少有研究关注到冲积河流三角洲对随机扰动的响应规律.三角洲分汊水道实际相当不稳定,对内部和外部扰动非常敏感,一个很小的结构差异就足以引发三角洲水道的重新分布.多年来,由于大型水库和水土保持工程的建设以及水文、气象、人类等不稳定因素的影响,我国江河湖泊内部发生了巨大的变化,特别是,异常变化的水沙通量.赣江-鄱阳湖区域三角洲上游在2020年夏季经历了有史以来最大的一次降雨,而在此之前,枯水期水位一直在明显下降,河床的强烈刷深和分汊河道的摆动、裁弯等活动致使该三角洲体系呈现出一些新的特征.水利工程和环保工程的许多短时尺度上的问题,如内部多汊水道的发展模式、上游河流与下游三角洲系统的连通性等,都需要从一个新的角度进行评估.
许多物理学家正越来越多地转向现代系统理论以拓展本领域的研究.其中,表示线性对象的输入与输出间关系的传递函数法获得了广泛应用.特别是对于具有高度规律性和交互性的非线性系统,如自然冲积河流系统,已有学者将降雨或流量因子作为噪声加入经典的确定性方程以追踪和识别丰富的河流演化过程,获取产汇流信息[13]、模拟水质量因子的概率演化过程[14]、研究河岸植被分布随流量变化的随机响应[15]、进行河相关系的随机微分建模等[16].这些方法为三角洲特征研究和流域管理提供了新的思路:将水流输入项视为随机源,通过概率化的研究来有效处理三角洲对内外扰动的响应问题.显然,前提是对三角洲随机演变特征的大量数据积累.
鉴于流量控制对三角洲形态发展有显著的影响,本文以入湖浅水三角洲为研究对象,采用物理模型方法,研究在不同量级恒定平均流量的控制条件下,三角洲水道对流量的确定性和非确定性响应特征.通过对比高、低流量情况下的重复试验结果,可以初步区分水流紊动特性和复杂泥沙环境对不同来水条件下水道发展的不同影响模式,加深对三角洲水道随机演变特性的理解.
1 试验设计
1.1 试验装置
本模型试验在天津大学河流动力学实验室自主研发的冲积三角洲模拟水池内完成(见图1)[17].工作空间(长3.6m,宽1.7m,高0.2m)沿纵向(方向)可分为3个功能区:进口区(=-0.5~0m)、三角洲发展区(=0~3.0m)和尾门区(=3.0~3.1m).水槽来水由水箱、流量计、蝶阀等控制,来沙由频率加沙器控制.可控的水沙循环供应系统保证了冲积河流-三角洲系统的可持续发展.水槽上方安装有图形监测处理系统,用于记录流场和地形信息.
1.2 试验方法
1.2.1 试验流程
(1)在进口区和三角洲发展区分别铺设10cm和5cm厚的天然非黏性沙.泥沙特性如图2所示,其中,中值粒径50=0.62mm,非均匀系数u=60/10=2.387,密度s=2650kg/m3.在此,采用非黏性沙便于阻止泥沙絮凝,并利于三角洲水道的自然形成与人工观察[5, 18].
(2)在进口区,利用薄玻璃板塑造6cm宽、5cm深的进口河道.
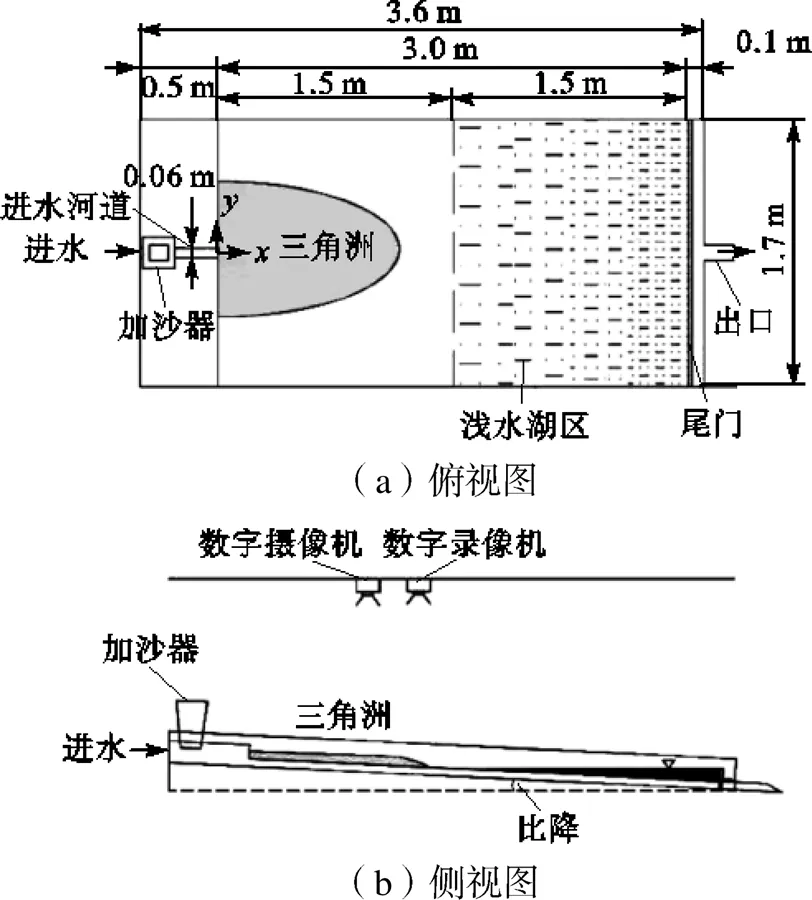
图1 试验设备示意

图2 试验所用泥沙的级配曲线
(3)调整水槽底部支架的高度以达到指定的水槽比降1%.在此,1%的比降值是经过前期预备试验的经验总结后精心挑选的,以保证实现三角洲完备的发展过程.
(4)从尾门处向浅水湖区缓慢注水直至达到设定的下游湖水位.
(5)分别启动水泵和加沙器,调节至指定来水流量和加沙频率,保持均值稳定,进行试验30h.
1.2.2 试验记录
(1)试验中每隔5min用摄像头记录模型三角洲的形态发展情况.
(2)每隔1h,关闭加沙器,利用示踪粒子法(PTV)[19]观测流场变化.
(3)每隔3h,逐渐关闭水泵和加沙器,待三角洲表面无水流时,利用激光测距仪测量地形.其中,激光测距仪精度为1mm,纵向测量间隔为10cm,横向测量间隔为2cm.
1.3 试验工况
影响入湖三角洲发展的因素主要包括来水特征、土壤地质构造、来沙特征和下游湖水位等.本团队已经在先前的工作中研究了后两者的影响规律,揭示了一些三角洲水道演化过程的随机特性[17, 20-21].如文献[2,5,12,22]中所述,来水特征严重影响着三角洲形成过程的泥沙输运能力和水道分汊程度,一个小的扰动就足以启动散乱水道的重新分布.冲积三角洲实际是一个随机演化的有机系统,因此,本团队设计了两种恒定平均流量控制并分别重复两次的试验工况,来探究来水特征对三角洲水道演化的确定性与非确定性影响规律.
本试验遵循Hooke[23]的“过程相似”规律.完全重现入湖浅水三角洲需要保证较低的弗劳德数(在0.1左右)和使得推移质运动在泥沙运动过程中占主导.因此,为了保证上游来水流速大于泥沙起动流速,及三角洲形态在试验过程中足够显著,基于前期试验经验,将两种主控流量定为50cm3/s和100cm3/s(流量计量程为0~100cm3/s),加沙速率s稳定为0.1cm3/s.具体工况设计参数见表1.
表1 试验工况设计参数
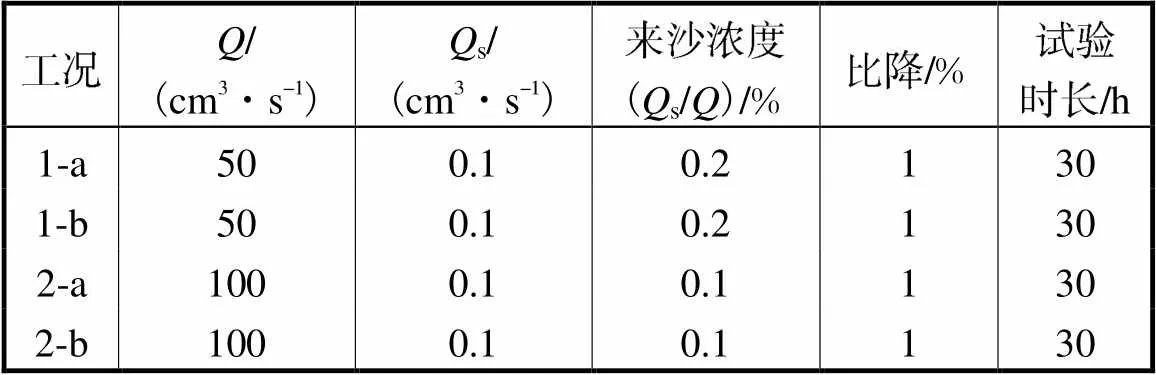
Tab.1 Design parameters of the experimental scenarios
2 结果与讨论
2.1 水道结构的演化过程
随着三角洲系统不断发展,其水道结构越发复杂.从试验中可以看到,在两种不同恒定平均流量分别作用下,各自重复试验得到的水道都会“准周期性”地表现出相似的形态特征,特别是一个单线型主河道与几个分汊河道的典型组合形态.然而,在试验大部分时间,水流都处于不规则的自适应调整过程.
图3所示为低流量控制下工况1重复试验的准周期相似的水道形态演化结果.在试验初始阶段的2h时(见图3(a)),水流明显受到非纵向扰动的影响:工况1-a和工况1-b的水道呈现沿轴的镜面对称发展趋势.从5h开始(见图3(b)~(f)),两组试验水道开始以平均4.5h的周期循环相似,尤其是其主流河道的走向.而在准周期相似的间隔期,从图3中的水道历史痕迹可见,水道演化经历了相当多的分汊、侧向摆动、废弃、再生等错综复杂的过程.结合试验录像记录总的来看,低流量控制下的三角洲水道发展过程,逐渐从起始阶段的周期性的堆积-下切为主,转变为水道的侧向摆动占主导.其中,工况1-a易偏向左侧摆动且通常回淤相对更早,工况1-b与其正好相反.
图4所示为高流量控制下工况2重复试验的准周期相似的水道形态演化结果.跟工况1相比,起始阶段水流受到非纵向的地质环境扰动较小,3h时第一次形态相似的水道还没出现分汊现象(见图4(a)).而从该时刻之后,水流开始变得更加不稳定,三角洲水道以平均4h的周期处于“向下游下切-分汊减弱”和“向上游回淤-分汊增强”的循环发展过程.整体来看,高流量下工况2汊道的侧向摆动明显弱于低流量下工况1.结合试验录像和图4中的水道历史痕迹观察,在“准周期相似”的间隔期,工况2-a与工况2-b也具有深刻而复杂的共性,只是工况2-b的水道较平缓地在三角洲中游区域“下切-回淤”,而工况2-a长时间处在三角洲下游区域强烈地下切,其偶尔的回淤过程非常迅速.

图3 工况1重复试验的准周期相似的三角洲水道

图4 工况2重复试验的准周期相似的三角洲水道
2.2 水道波动特征的统计分析
对模型三角洲水道的定性观察显示,只有部分准周期相似的单线型主流河道值得足够的信任,而频繁分汊、摆动的大量水道具有很大的时空不确定性.因此,本节针对水道几何特征,提取包括主流水道长度、水道分汊位置、水道分汊角度及汊道长度s等定量指标,进行三角洲水道波动特征的统计分析,以定量地理解流量对三角洲水道演变的复杂影响规律.图5为水道形态结构平面几何特征的定量分析示意.图中,“O”表示河道发展的原点,“M”表示主流水道,沿着主水流方向,其左侧汊道以“L”表示,左侧汊道以“R”表示,L、R分别为左侧汊道和右侧汊道的分汊角度.
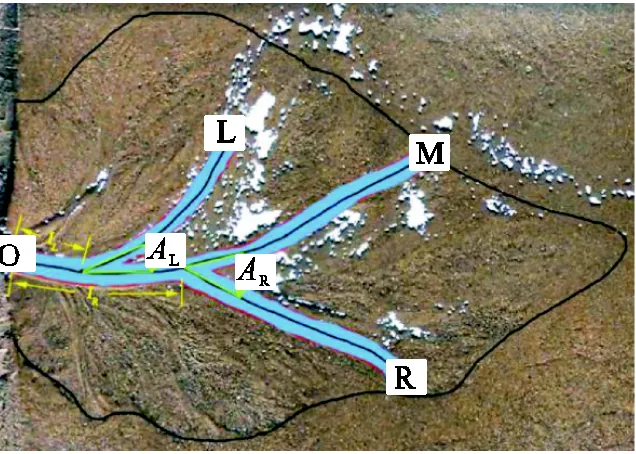
图5 水道形态结构的平面几何特征示意
2.2.1 水道长度指标——主流水道长度
图6(a)、(b)中,每组的主流水道长度都具有独特的波动周期和波动强度,前面的“准周期相似”的水道演化现象可以理解为是在同一恒定平均流量控制条件下,水道长度波动曲线交点的一种显性表达.在工况1中,通过回归分析得到的曲线相交周期为3.08h,比定性观察得到的周期值4.5h略小;而工况2中曲线相交的回归周期为6h,比定性观察值4h略大.这意味着,对于单线型主流水道而言,低流量下长度指标统计分析的确定度高于其定性的形态观察,而高流量下情况正好相反.也就是说,低流量下水流面临的复杂泥沙环境和高流量下水流自身的不稳定性,是两种不同量级流量控制试验相应的主要不稳定根源.此外,图6(a)中工况1-a较大的波动周期和图6(b)中工况2-b平缓的波动变化及其较小的平均值,也与前文中提到的定性结论如“工况1-a的水道常常回淤相对较早;工况2-b的水道结构常围绕在三角洲中游区域周期性地‘下切-回淤’”相吻合.
通过进一步地观察图6可知,所有主河道长度的波动特征值(包括平均值、平均波幅、平均周期),及两种重复试验所得指标相应均值的结果偏差(图6(c)、(d)),均随着流量的增大而增大.工况1的重复试验结果中,平均波幅与平均周期都随其平均值的增大而增大;工况2中平均周期依然随其平均值正向变化,但平均波幅却保持稳定(尽管波动过程不同).考虑到平均周期和平均波幅在一定程度上可以分别代表扰动源的性质和能量级别,因此本节分析不仅成功展示了泥沙输运和水流脉动对指标平均波动周期的不同影响规律,而且揭示了高流量条件下各因素对指标平均波幅的稳定效应,以及低流量条件下由于水道大幅分汊、侧向摆动等对指标平均波幅的弱化效应.
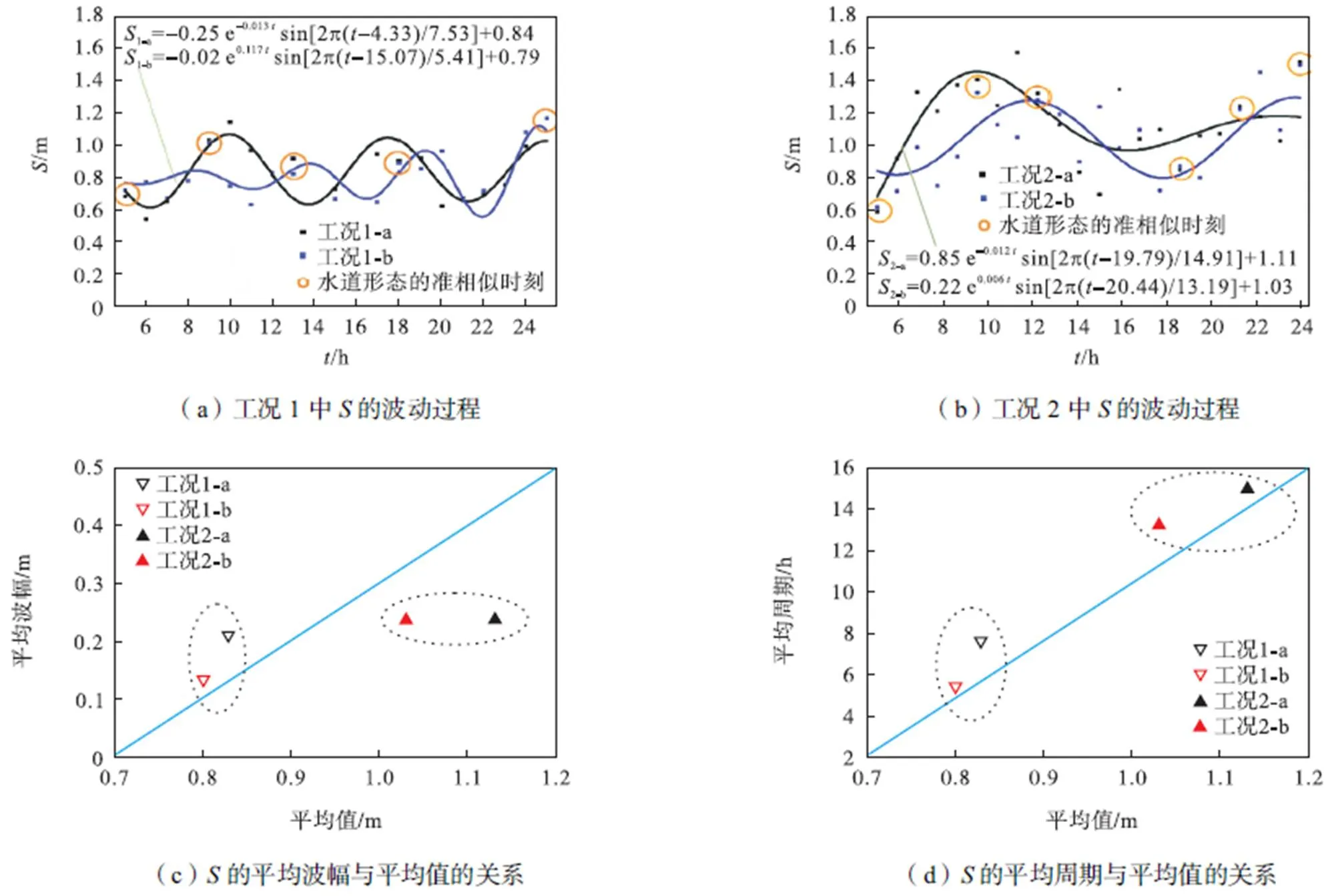
图6 不同控制条件下试验所得主流水道长度指标S的波动特征
2.2.2 起点距指标——汊道分汊位置
图7所示为不同控制条件下试验所得汊道分汊起始点与主河道原点的距离——起点距指标的波动特征曲线.其中,沿主流方向,将首次出现的可以完整发育的汊道命名为“一级汊道”(并按向左/向右分汊,分别称为左侧/右侧一级汊道),再向下游发展的汊道统称为“二级(及以上)汊道”.
从确定性的方面看(见图7(a)、(b)),起点距指标的均值在一级汊道情况下随流量正向变化,在二级(及以上)汊道情况下保持稳定.①对于一级汊道情况,指标的平均波幅和平均周期与其均值分别呈正相关和反相关关系,其中工况1指标整体平均的波动周期远远大于指标相应的周期值(对比图7(b)和图6(d));②对于二级(及以上)汊道情况,指标的平均波幅和平均周期都与流量呈反相关变化关系.
从非确定性的角度来看,在工况1重复试验的左-右侧一级汊道中,指标的平均波幅和平均周期都与其均值呈正相关变化关系;在工况2重复试验中,指标平均周期与其均值反向变化,而平均波幅几乎不随均值变化.
由此可以看出,本节研究再次凸显了低流量条件下波动指标的周期和高流量条件下波动指标的波幅的反常特性.特征总结见表2.
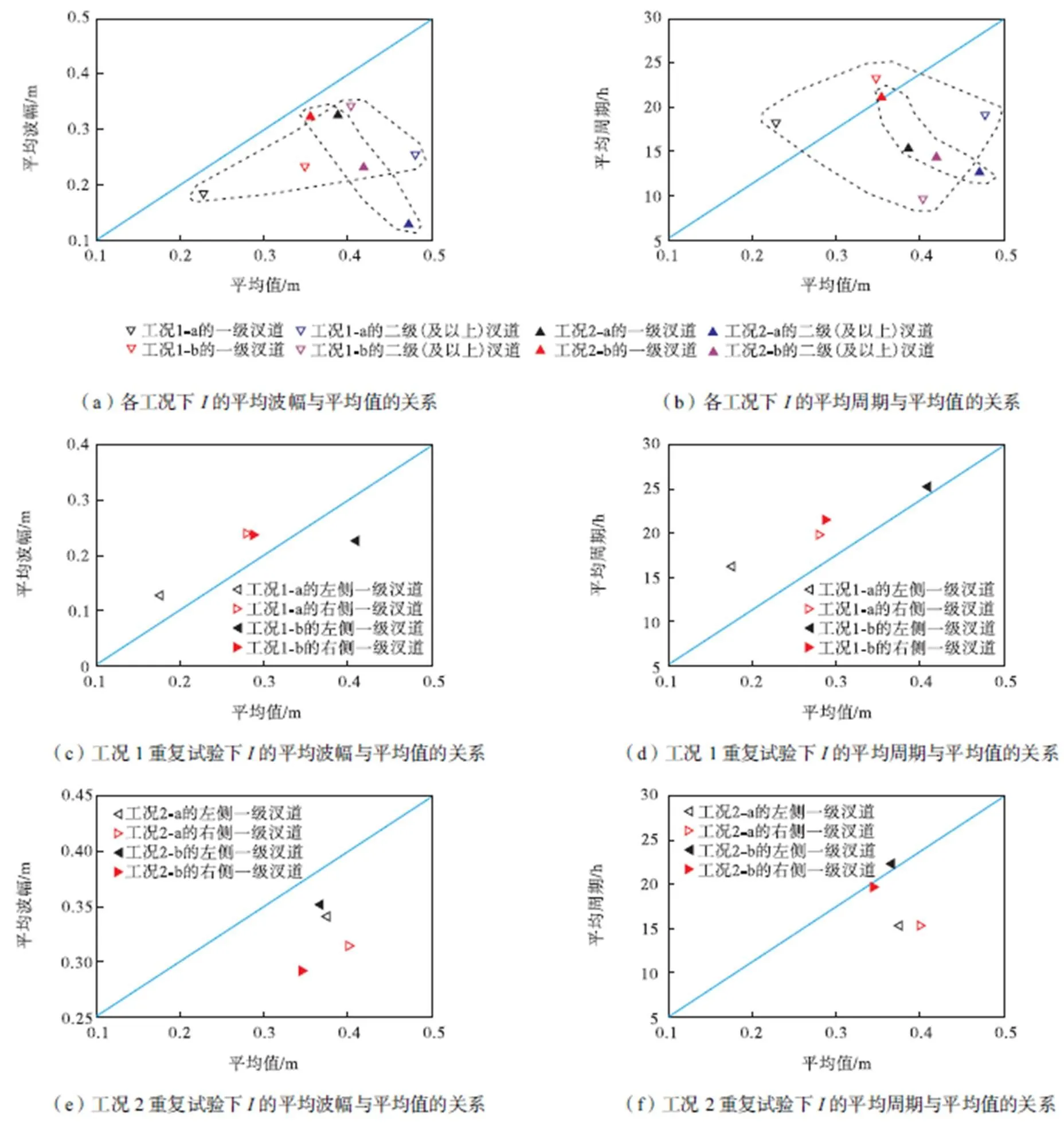
图7 不同控制条件下试验所得不同层级汊道的起点距指标I的波动特征
表2 流量对多级汊道几何特征的确定性影响和对一级汊道几何特征的非确定性影响特征总结

Tab.2 Summary of the deterministic effects of discharge on the different-order channels and nondeterministic effects on 1st branches in the aspect of geometrical characteristics
注:“正”表示正相关;“负”表示负相关;“-”表示无关;“/”表示不做直接判断.
2.2.3 分汊角指标——汊道分汊角度
图8所示为不同控制条件下试验所得汊道分汊方向与主河道发展方向的夹角——分汊角指标的波动特征分析曲线.从确定性方面、多级汊道间的比较来看(见图8(a)、(b)),的平均波幅和平均周期都同其平均值一样、随着流量的增大而增大,唯一的例外是二级(及以上)汊道中平均周期与其均值的负相关变化关系.而对于可能的非确定性方面,由图8(c)~(f)可见,不管在低流量条件还是高流量条件下,重复试验得到的左/右侧一级汊道中,的平均波幅和平均周期都与其平均值呈正相关变化关系.总的来看,各项统计特征间的正相关关系与前文分析的主河道长度指标的相关变化规律一致.

图8 不同控制条件下试验所得不同层级汊道的分汊角指标A的波动特征
2.2.4 汊道长度指标*
图9所示为不同控制条件下试验所得汊道长度指标的波动特征曲线.从确定性方面(见图9(a)、(b))看,与指标相似,指标的平均波幅、平均周期及平均值都随着流量的增大而增大,例外部分是二级(及以上)汊道中略微减弱的平均周期.而从重复试验结果中观察非确定性方面得到的结果(见图9(c)~(f))可知,平均波幅和平均周期与其相应均值的关系为:在低流量条件下全是负相关,在高流量条件下全是正相关.显然,本节研究又凸显了低流量工况试验的异常特性.特征总结见表2.
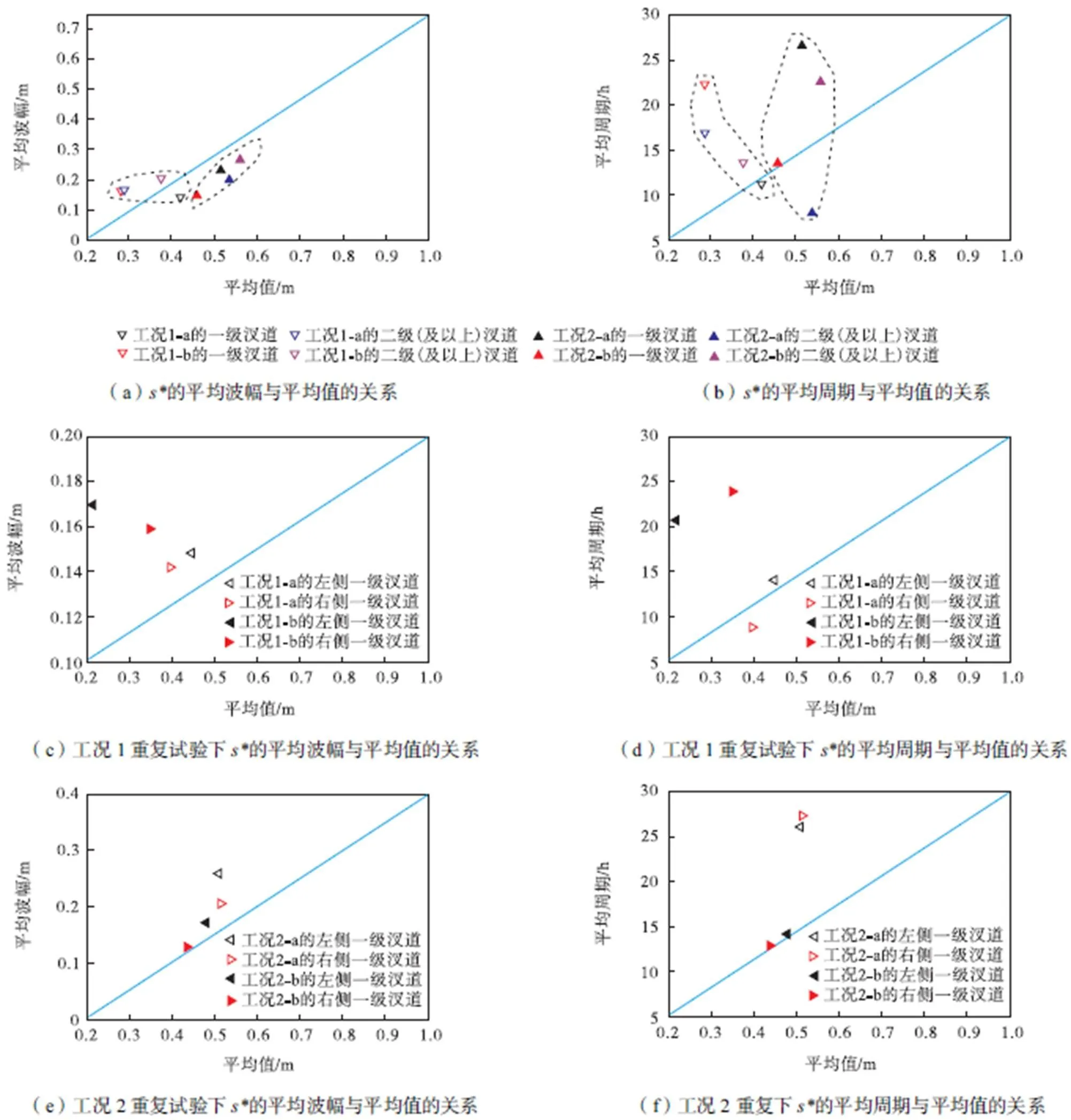
图9 不同控制条件下试验所得汊道长度指标s*的波动特征
2.3 特征关系讨论
通过对模型三角洲主-汊水道几何特征指标(包括、、和*)的波动参数(包括平均值、平均波幅和平均周期)的统计分析,可以看到流量对主流水道和汊道的确定性影响规律主要为:①单线型主流水道长度指标和流量的特征关系基本都是正向的(除了高流量控制条件下稳定的平均波幅);②对于汊道的发展,指标(、和*)响应流量变化的完全相同的特征关系模式为:一级汊道中指标平均值和平均波幅(随流量变化)的正向变化,二级(及以上)汊道中指标平均周期(随流量变化)的负向变化;相对异常的关系模式为:一级汊道中起点距指标的平均周期与流量的关系,二级(及以上)汊道中起点距指标的平均值和平均波幅与流量的关系.图10所示为模型汊道几何特征指标随流量增大的确定性关系示 意图.
基于确定性的特征关系,在两种重复试验组内对左/右侧一级汊道的指标波动特征进行分析,从非确定性方面观察流量对试验结果的影响规律:分汊角指标的波动特征与流量都呈正相关变化关系,从整体到局部都未发现该指标的非确定性特征关系;几种指标中最显著的不确定性特征在于,低流量控制条件下起点距指标平均周期与其平均值的正相关关系,汊道长指标*平均波幅和平均周期与其平均值的反相关关系.
这表明,伴随主流水道长度指标随流量的增大而增大,最值得关注的是在三角洲中游起点距指标的3个波动特征参数为非正向变化,指标、和*平均周期为负向变化(在高流量控制条件下起点距指标的平均值约为0.44m,相对1m左右的三角洲整体纵向发展尺度,可称为三角洲中游).与此同时,从低流量控制条件下三角洲上游汊道起点距指标和长度指标*的平均周期与相应平均值的波动特征关系中,可以清楚地观察到流量在三角洲水道分汊演变过程中的非确定性影响(低流量条件下起点距指标的平均值约为0.28m,可称为三角洲上游).显然,在局部区域和局部方向上的泥沙堆积体,是一个重要的待解扰动源.
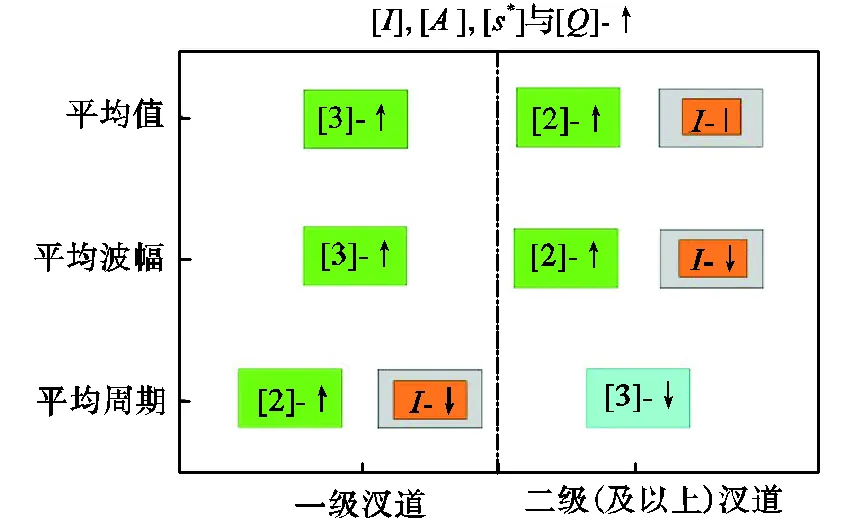
注:[3]表示汊道全部3个指标,[2]表示其中的2个指标;“↑”表示增大,“↓”表示减小,“|”表示不变
3 结 论
三角洲形成与演化过程中,来水特征可以影响水道发生各种各样多层次的结构变化.本文通过不同恒定平均流量作用下的入湖三角洲发展重复试验,研究了流量对三角洲水道的确定性与非确定性影响规律.
(1)定性观察方面,模型水道演化过程中既具有准周期相似性,也含有丰富的随机特性.随着整体不断发展,高流量条件下的三角洲水道在“向下游下切、同时分汊减弱”和“向上游回淤、同时分汊增强”之间周期性地循环往复,而低流量条件下成熟发展的三角洲主要由周期性的“水道强烈分汊与频繁的侧向摆动”过程主导.
(2)定量观测水道几何特征,一方面(确定性地),主流水道长度指标随流量保持正相关变化的同时,伴随有三角洲中游区域、汊道分汊起点距指标波动参数的非正相关变化和汊道各几何指标波动周期的负相关变化;另一方面,最为凸显的非确定性特征是低流量条件下三角洲上游、汊道起点距指标和汊道长度指标各自的波动周期与相应均值的正相关和负相关变化.
本文采用的研究方法及对三角洲水道丰富的随机特性的研究,对于加深对三角洲“生态活性”的理解具有重要的创新意义和应用价值.未来,本团队将通过更多相似的重复试验研究,尝试对三角洲水道形态的概率分布特征进行深度地解析.
[1] Guo R F,Zhu Y Q,Liu Y B. A comparison study of precipitation in the Poyang and the Dongting Lake Basins from 1960-2015[J]. Scientific Reports,2020,10(1):1-12.
[2] Whipple K X,Trayler C R. Tectonic control of fan size:The importance of spatially variable subsidence rates[J]. Basin Research,1996,8(3):351-366.
[3] Hartley A J,Mather A E,Jolley E,et al. Climatic controls on alluvial-fan activity,Coastal Cordillera,northern Chile[J]. Geological Society London Special Publications,2005,251(1):95-116.
[4] Harvey A M. Differential effects of base-level,tectonic setting and climatic change on quaternary alluvial fans in the northern Great Basin,Nevada,USA[J]. Geological Society London Special Publications,2005,251(1):117-131.
[5] Clarke L,Quine T A,Nicholas A. An experimental investigation of autogenic behaviour during alluvial fan evolution[J]. Geomorphology,2010,115(3/4):278-285.
[6] Jerolmack D J,Paola C. Complexity in a cellular model of river avulsion[J]. Geomorphology,2007,91(3/4):259-270.
[7] Nicholas A,Quine T. Crossing the divide:Representation of channels and processes in reduced-complexity river models at reach and landscape scales[J]. Geomorphology,2007,90(3/4):318-339.
[8] Nicholas A P,Quine T A. Modeling alluvial landform change in the absence of external environmental forcing[J]. Geology,2007,35(6):527-530.
[9] Ashworth P J,Best J L,Jones M. Relationship between sediment supply and avulsion frequency in braided rivers[J]. Geology,2004,32(1):21-24.
[10] Davies T R,Korup O. Persistent alluvial fanhead trenching resulting from large,infrequent sediment inputs[J]. Earth Surface Processes and Landforms,2007,32(5):725-742.
[11] Kim W,Jerolmack D J. The pulse of calm fan deltas[J]. The Journal of Geology,2008,116(4):315-330.
[12] Van Dijk M,Postma G,Kleinhans M G. Autocyclic behaviour of fan deltas:An analogue experimental study[J]. Sedimentology,2009,56(5):1569-1589.
[13] Mondal M S,Wasimi S A. Periodic transfer function-noise model for forecasting[J]. Journal of Hydrologic Engineering,2005,10(5):353-362.
[14] Boano F,Revelli R,Ridolfi L. Stochastic modelling of DO and BOD components in a stream with random inputs[J]. Advances in Water Resources,2006,29(9):1341-1350.
[15] Tealdi S,Camporeale C,Ridolfi L. Modeling the impact of river damming on riparian vegetation[J]. Journal of Hydrology,2011,396(3/4):302-312.
[16] 宋晓龙,钟德钰,王光谦. 河相关系的随机微分方程建模与研究[J]. 水利学报,2019,50(3):364-376.
Song Xiaolong,Zhong Deyu,Wang Guangqian. Modeling and research of stochastic differential equations of hydraulic geometry relationship[J]. Journal of Hydraulic Engineering,2019,50(3):364-376(in Chinese).
[17] 白玉川,胡 晓,徐海珏,等. 入湖浅水三角洲形成过程实验模拟分析[J]. 水利学报,2018,49(5):549-560.
Bai Yuchuan,Hu Xiao,Xu Haijue,et al. Experimental analysis of the formation process of lacustrine shallow-water delta[J]. Journal of Hydraulic Engineering,2018,49(5):549-560(in Chinese).
[18] Hoyal D,Sheets B. Morphodynamic evolution of experimental cohesive deltas[J]. Journal of Geophysical Research,2009,114:F02009.
[19] 白玉川,许 栋. 复杂表面流场中粒子跟踪测速的研究[C]//第20届全国水动力学研讨会文集. 北京,中国,2007:430-438.
Bai Yuchuan,Xu Dong. Study on particle tracking velocimetry in complex surface flow field[C]//Proceedings of the 20th National Conference on Hydrodynamics. Beijing,China,2007:430-438(in Chinese).
[20] 徐海珏,胡 晓,白玉川,等. 入湖三角洲形成过程与淤积形态变化的实验研究[J]. 水力发电学报,2019,38(1):52-62.
Xu Haijue,Hu Xiao,Bai Yuchuan,et al. Experimental study on formation and morphologic evolution of alluvial lake deltas[J]. Journal of Hydroelectric Engineering,2019,38(1):52-62(in Chinese).
[21] Xin W Y,Bai Y C,Xu H J. Experimental study on evolution of lacustrine shallow-water delta[J]. Catena,2019,182:104125.
[22] Van Dijk M,Kleinhans M G,Postma G,et al. Contrasting morphodynamics in alluvial fans and fan deltas:Effect of the downstream boundary[J]. Sedimentology,2012,59(7):2125-2145.
[23] Hooke R L. Model geology:Prototype and laboratory streams:Discussion[J]. Geological Society of America Bulletin,1968,79(3):391-394.
Experiments on Stochastic Response Characteristics of Lacustrine Deltaic Channels to Discharge
Xu Haijue1, 2,Song Xiaolong1, 2,Bai Yuchuan1, 2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300350,China;2. Institute for Sedimentation on River and Coastal Engineering,Tianjin University,Tianjin 300350,China)
The development of river-delta systems exhibits some stochastic characteristics even under slow-varying external conditions,which pose considerable uncertainties for environmental monitoring and resource management on deltas. Instead of using traditionally deterministic investigation methods,in this study,we used two sets of repeated physical modeling experiments under two average-constant discharge conditions to explore both deterministic and nondeterministic effects of the upstream river-inflow on channelized configurations of a lacustrine shallow-water delta. The qualitative observations and quantitative statistics of the fluctuations of the geometrical characteristics of the obtained quasi-periodically similar deltaic channels show that,on the one hand,deterministically,along with the change of discharge,the single-main channel length increased positively,and both the fluctuation characteristics of the branching position indicator of different-order branching channels and the average period of all the geometrical indicators of higher-order branching channels in the middle delta underwent nonpositive changes;on the other hand,non-deterministically,results highlighted the positive and negative correlations between average period and average value,on the indicators of the branching position and the branching channel length respectively in the upper delta under low-discharge conditions. This study improves our understanding of bifurcation instability and makes the foundation for stochastic modeling of lacustrine-delta morphology.
lacustrine delta;discharge;channelized configuration;deterministic and nondeterministic;physical modeling experiment
TV147
A
0493-2137(2022)01-0101-10
10.11784/tdxbz202101058
2021-01-27;
2021-05-18.
徐海珏(1977— ),女,博士,副教授,xiaoxiaoxu_2004@163.com.
宋晓龙,xlsong@tju.edu.cn.
国家自然科学基金资助项目(51879182).
Supported by the National Natural Science Foundation of China(No. 51879182).
(责任编辑:樊素英)
