FRP约束矩形高强钢管混凝土长柱轴压性能有限元分析

杜颜胜，高鼎辉，陈志华，郑子晗, 3

FRP约束矩形高强钢管混凝土长柱轴压性能有限元分析

杜颜胜1, 2，高鼎辉1，陈志华1, 2，郑子晗1, 3

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；3. 天津市政工程设计研究总院有限公司，天津 300372)

以纤维增强复合材料(FRP)约束矩形高强钢管混凝土长柱的轴压试验为基础，利用有限元软件ABAQUS对FRP约束矩形高强钢管混凝土长柱进行了非线性有限元分析，有限元分析结果和试验荷载-位移曲线吻合较好，破坏模态一致，峰值荷载偏差平均值仅为0.5%，方差为0.080，验证了材料本构关系、单元类型、接触和边界条件等建模方法的可靠性，表明该有限元模型可以准确预测其轴压性能．基于试验和数值模拟分析了试件的受力机理：薄壁钢管在压应力较小时发生局部屈曲；混凝土在钢管鼓曲处发展了塑性应变和横向变形；由于倒角较小，FRP在角部存在应力集中现象，在鼓曲最严重处发生断裂．环向FRP约束延缓了钢管局部屈曲的萌生和发展，提高了核心混凝土的约束强度，对于内填普通强度(C40)混凝土的钢管混凝土柱，环向FRP在承载力上的提升作用较明显，方矩形截面试件的峰值承载力提高了6%～7%．对于内填高强度(C80)混凝土的钢管混凝土柱，方矩形截面试件的峰值承载力提高了4%～5%．最后利用该有限元模型探究了长细比参数对轴压性能的影响，结果表明：FRP对承载力的提升效果随着长细比的增大而降低，对倒角半径为20mm的模型，当长细比达到31.3时，环向FRP仍能为柱提供有效约束，提升柱11%的峰值承载力．

纤维增强复合材料；高强钢管混凝土长柱；轴压性能；非线性有限元分析；长细比

近年来，纤维增强复合材料(fiber reinforced polymer，FRP)因其轻质、高强、抗腐蚀、耐疲劳和施工方便等特点在土木工程中得到了越来越广泛的应用[1]．钢管混凝土凭借出色的力学性能自出现起就受到工程师们的重视，学者们对其展开了大量研究[2-4].利用外包FRP来约束钢管混凝土结构，在限制钢管局部屈曲的同时，FRP与钢管一起对核心混凝土提供约束作用．在不增大截面面积及结构自重、不加大高强钢材用钢量的前提下，提高构件的静力性能和耐腐蚀性，充分发挥材料的轻质高强优势．

一些学者对FRP约束钢管混凝土柱轴压性能进行了试验和理论研究．文献[5-7]开展了FRP约束钢管混凝土短柱和中长柱的轴压试验，研究了横纵向FRP层数、混凝土强度和长细比等对试件承载力及破坏形式的影响．文献[8]通过单调轴压试验研究了 FRP 约束高强椭圆钢管混凝土柱的轴压性能，研究变量包括 FRP 层数和截面长宽比．文献[9]进行了碳纤维增强复合材料(carbon fiber reinforced polymer，CFRP)约束圆钢管混凝土短柱轴压试验，采用普通混凝土和高强混凝土进行对比，研究了径厚比、混凝土强度和CFRP层数的影响．

当前的研究成果主要集中于普通强度混凝土和普通强度钢材，对于高强度材料特别是同时采用高强混凝土和高强钢的研究并不多．同时，目前的研究针对的大部分为圆截面，少部分为方截面，鲜有矩形截面的相关研究．矩形钢管混凝土柱在节点构造、截面灵活性上有着突出优势，进行矩形截面钢管混凝土构件的研究十分必要．此外，目前对于FRP约束钢管混凝土轴压构件的研究多为短柱的极限承载力研究，对于工程中应用的长柱的稳定性研究较少，有待进一步补充．为此，本文在已经完成的FRP约束矩形高强钢管混凝土长柱轴压性能试验研究[10]的工作基础上，为了对其受力和变形性能进一步分析，采用大型通用有限元分析软件ABAQUS建立了FRP约束矩形高强薄壁钢管混凝土柱的轴压模型，进行了数值模拟分析，通过试验现象与荷载-位移曲线的对比，验证了模型的准确性以及该数值模拟所采用的混凝土本构参数的合理性．最后，对长细比对承载力的影响进行了参数化分析，可为工程应用提供理论基础和技术参考.

1 试验概况

本试验为模拟中长柱沿单轴方向失稳，采用铰接的边界条件，可选择刀铰或圆柱铰．刀铰具有对中准确、加工安装方便的优势，在试验中应用较为广泛，但由于其接触面较小，仅通过尖端施加荷载，故在荷载较大时易发生变形，导致试验结果不准确．圆柱铰接触面较大，可避免这一问题，但加工制作以及安装过程较为复杂，并且由于其端部为一个曲面，实际对中的准确性很难保证．由于本试验中试件均为足尺截面高强度材料，预估荷载较大，设计并使用圆柱铰进行试验．为使圆柱铰与对应凹槽准确对中，在上下端板上均焊接两道短肋以固定凹槽防止其发生滑动．试件安装示意图如图1所示．

表1 试件参数

Tab.1 Specimens parameters

注：为截面高度；为截面宽度；y为实测钢材屈服强度；cu为实测混凝土立方体抗压强度；u为理论计算承载力．

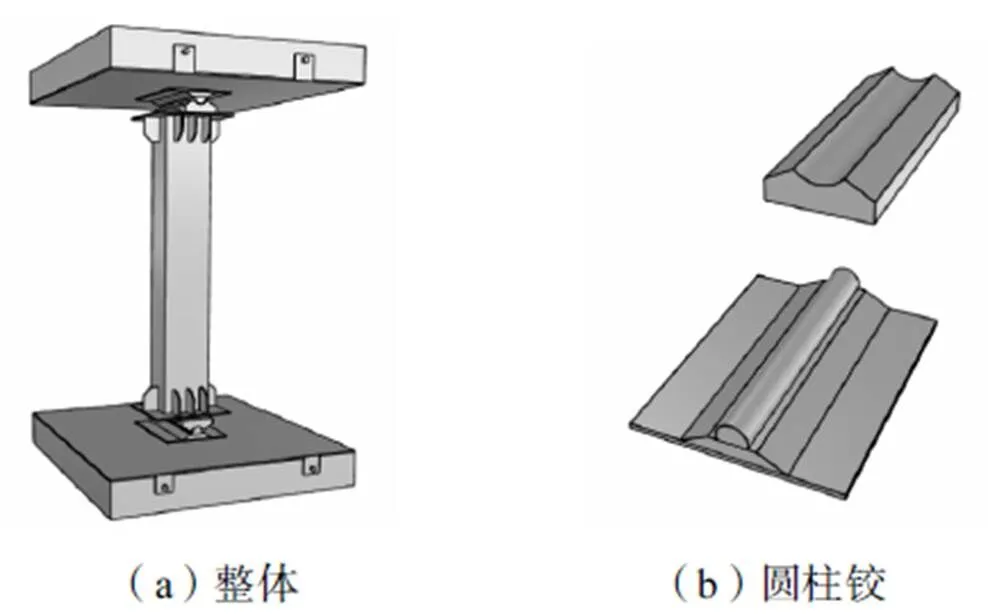
图1 试件安装示意

试验采用分级加载制度：在加载初期采用荷载控制，按照理论计算承载力的1/10大小分级加载；在达到峰值荷载的80%后，采用位移控制加载，加载速率0.3mm/min，直至试件破坏，试验结束．典型试件加载图如图2所示．

图2 典型试件加载图

2 有限元模型的建立

2.1 材料本构关系

2.1.1 核心混凝土本构

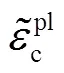
图3 混凝土塑性损伤模型的应力-应变关系

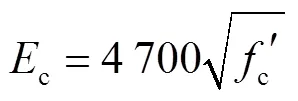
在FRP与钢管的复合约束下，核心混凝土处于三向受压状态，其受力特点与钢管混凝土结构类似，主要与约束效应系数以及截面倒角半径有关．本文基于文献[12]提出的矩形钢管混凝土中核心混凝土的受压本构关系，考虑FRP与钢管复合约束作用以及截面倒角的影响，对核心混凝土的峰值强度进行了修正．修正后的混凝土等效应力-应变关系的函数表达式为

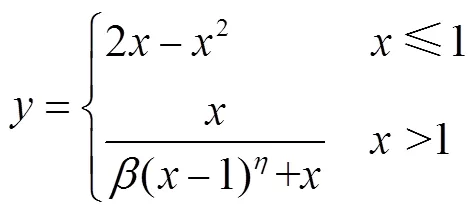
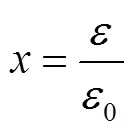
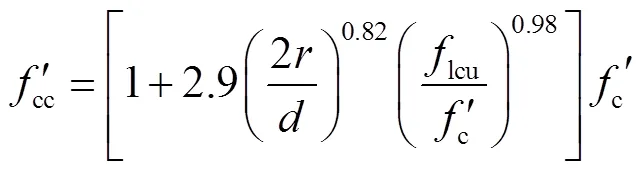
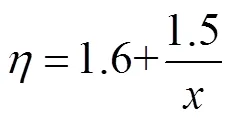
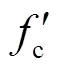
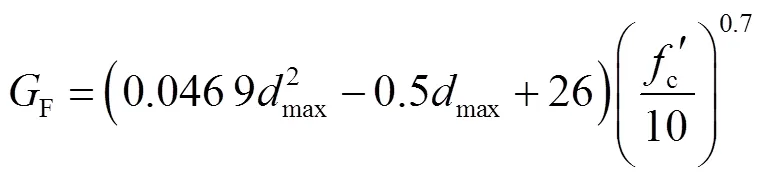
2.1.2 钢 材

文献[13]指出在矩形钢管混凝土结构中，由于钢管屈曲发展较快，基本不会利用到钢材的强化段，且本文采用的薄壁高强钢管的临界屈曲应力较小，对于核心混凝土的约束作用也是有限的，故采用钢材的理想弹塑性模型进行模拟，其应力-应变关系如图4所示，钢材屈服强度为731.9MPa，其弹性模量s＝2.06×105MPa，泊松比为0.3．

端板、凹槽及圆柱铰仅作为传力装置，对试件的承载能力没有影响，故将其作为刚体考虑，弹性模量设置为100s．肋板钢材采用二折线模型，屈服强度为345MPa，s＝2.06×105MPa．

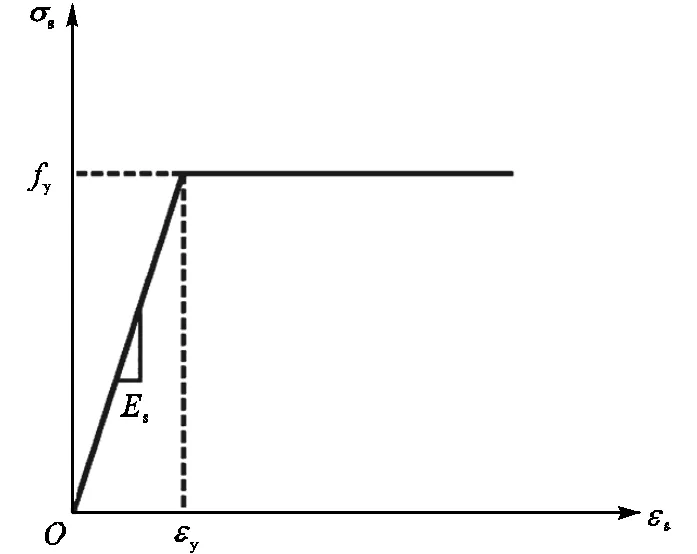
图4 高强钢材的应力-应变关系曲线

2.1.3 CFRP

碳纤维布为各向异性材料，沿柱轴向没有刚度，仅能沿纤维方向承受拉力，在达到极限应力前为线弹性．当达到极限拉应力后，纤维发生脆性断裂从而丧失承载能力，其应力-应变关系如图5所示．

本文中利用传统壳单元(conventional shell)的建模方式来模拟FRP布的受力性能．这种方式通过在参考曲面上定义几何形状来离散化物体，可通过截面属性定义厚度，节点拥有位移和旋转自由度．为了更准确方便地模拟复合材料的叠层效果，本文还利用铺层功能(composite-layup)对多层复合材料进行铺层设计，定义每一层结构的铺设区域、材料、铺设的厚度和角度等．在后处理中，可单独显示每一个铺层的应力、应变和损伤等以便进行分析．

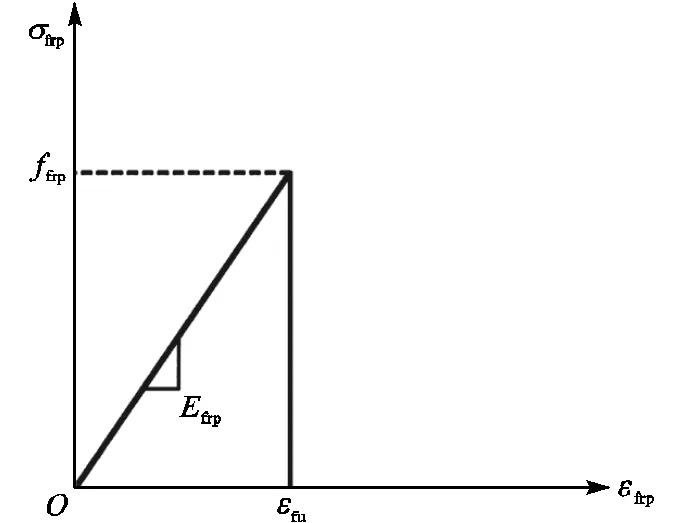
图5 CFRP的应力-应变关系曲线

本文采用Hashin Damage模拟各向异性的弹脆性材料的损伤萌生、发展和失效破坏，损伤通过材料刚度的退化来实现，这在纤维增强复合材料的分析中起着重要作用．

刚度逐步退化的过程采用损伤力学建模，由Hashin准则来判断损伤的产生，而损伤的演化规律则是基于损伤过程和线性材料刚度退化过程中的能量耗散理论．

损伤模型共包含4种：拉伸时的纤维断裂，压缩时的纤维屈曲和扭结，横向拉伸和剪切时的基体断裂，横向压缩和剪切时的基体破碎．相关参数如表2所示．

表2 CFRP的Hashin损伤参数

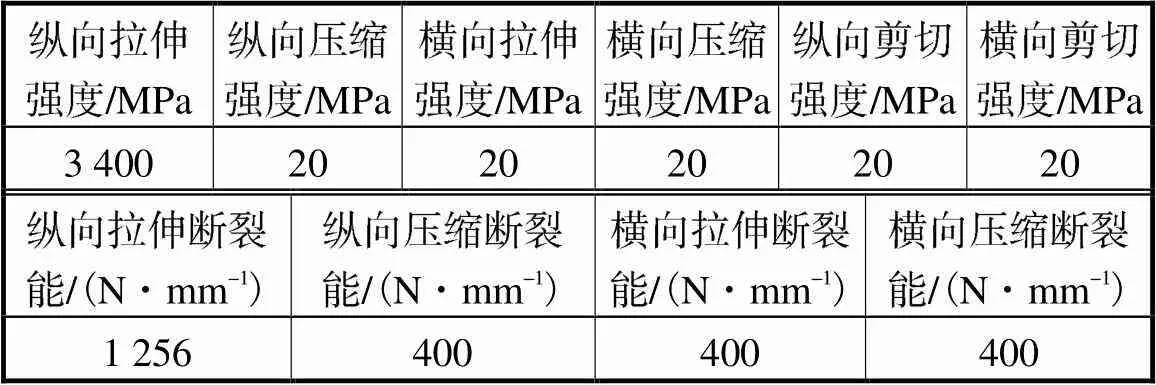
Tab.2 Hashin damage parameters of CFRP

假定纤维增强复合材料中的各条纤维是平行的，结构以单向板(lamina)表示，如图6所示，单向板位于1-2平面内，其中1方向为纤维方向．

图6 单向板

通过输入正交各向异性的材料属性，实现对材料未损伤时力学性能的定义，CFRP布的材料属性如表3所示．

表3 CFRP材料属性

Tab.3 Material properties of CFRP

注：u12为泊松比；1和2为2个方向的弹性模量；12、13和23分别为3个方向的剪切模量．

2.2 单元选取和网格划分

轴压FRP约束矩形钢管混凝土长柱模型由3部分组成：混凝土、钢管和CFRP．混凝土采用8节点缩减积分三维实体单元(C3D8R)；钢管为薄壁高强钢管，其厚度方向尺寸远小于其他两个方向，故采用4节点缩减积分壳单元(S4R)，厚度方向采用5个积分点的Simpson积分，其相比实体单元具有更高的计算效率同时还能保证准确性；CFRP布采用4节点缩减积分壳单元(S4R)，其相比膜单元具有更好的收敛性，且可用于ABAQUS的复合材料铺层功能．此外，本文还建立了端板、凹槽和圆柱铰以模拟实际受力情况，三者均采用8节点缩减积分三维实体单元(C3D8R)．

本文采用结构化网格划分技术对模型进行了单元划分，为了保证收敛性，使钢管、混凝土与FRP的网格最大程度对齐．经过一系列试算，确定了合理的网格尺寸以保证计算效率和计算结果的准确性，如图7所示．在模型中对钢管的倒角也进行了模拟，＝5mm．

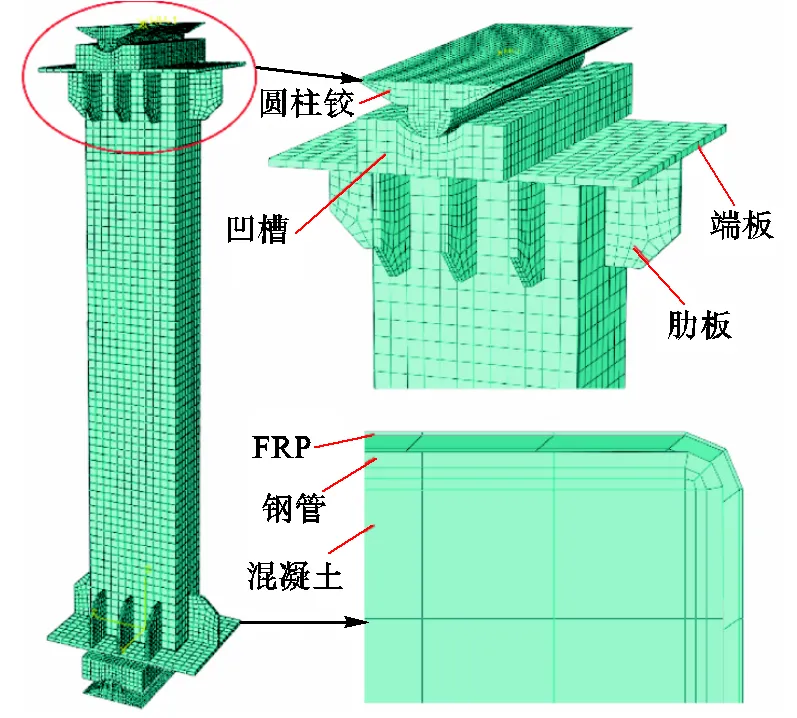
图7 网格划分

2.3 接触和边界条件

本文中钢管与混凝土的界面关系采用接触(contact)模拟，切向接触选择库伦摩擦模型中的罚函数(penalty)，摩擦系数取0.25，法向接触采用硬接触(hard contact)并允许接触面发生分离．由以往研究可知，FRP约束钢管混凝土柱在受力过程中几乎不发生FRP的脱胶现象，其与钢管可协同工作，故FRP与钢管的界面关系采用绑定(tie)关系．

模型的边界条件如图8所示．钢管端部与端板的连接、凹槽与端板的连接以及肋板与钢管、端板的连接均采用绑定(tie)，混凝土端部与端板的接触、圆柱铰与凹槽接触处的连接均采用法向硬接触(hard contact)．上端圆柱铰顶面耦合至参考点RP-1，约束其除向位移外的所有自由度，下端圆柱铰底面耦合至参考点RP-2，约束RP-2的所有自由度．

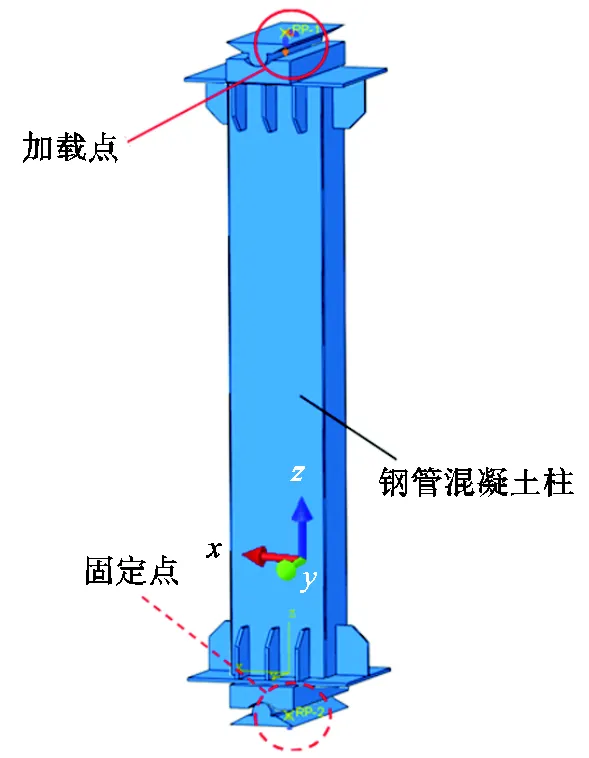
图8 边界条件

3 有限元模型的验证和受力机理分析

通过特征值屈曲分析，得到钢管的1阶屈曲模态如图9所示，以此作为试件的初始缺陷，初始缺陷取值为/1000．

轴压长柱典型试件的试验破坏模态与有限元分析结果对比如图10所示．对于无约束长柱，破坏形式主要表现为端部或近端部钢管严重鼓曲，核心混凝土在鼓曲处发展压缩损伤，最终被压碎，S试件在端部或近端部发生弯折、转动，如图10(a)、(c)所示；对于FRP约束长柱，破坏表现为钢管外鼓最严重处的FRP发生断裂并退出工作，最终该位置核心混凝土被压碎，试件在端部或近端部发生弯折、转动，如图10(b)、(d)所示．

试件的荷载-位移曲线对比如图11所示．总地来说，有限元曲线在弹性段、弹塑性阶段以及下降段与试验曲线吻合较好，但仍存在一些差异，表现为有限元分析结果中的初始刚度略大于试验值．原因可能是在浇筑长柱试件混凝土时，由于钢管截面尺寸较小，人工灌注和振捣过程一般会导致混凝土存在空隙和不密实等情况，使得试件整体刚度要小于有限元模型中的理想密实状态，截面承载能力也受到核心混凝土密实程度的影响．

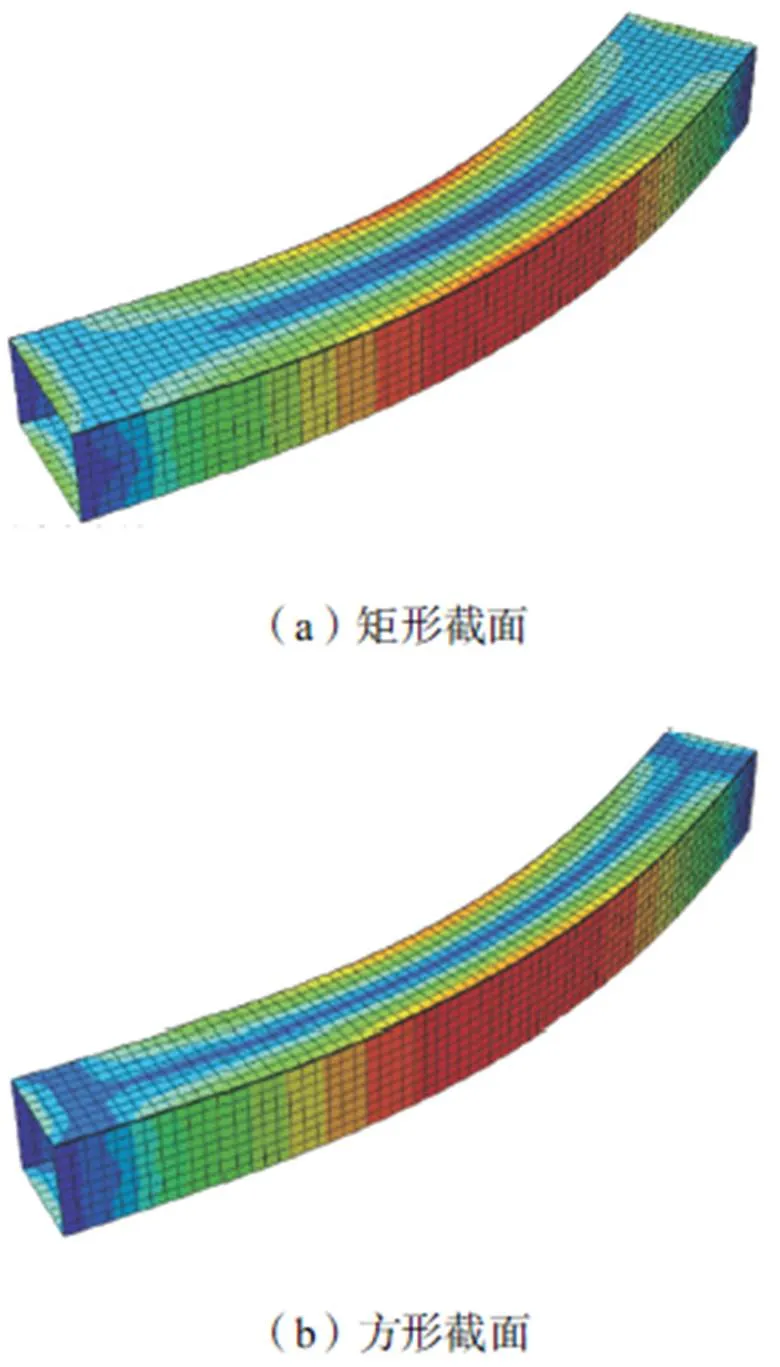
图9 钢管的1阶屈曲模态

各试件峰值荷载的有限元值与试验值之比如表4所示．均值为0.995，方差为0.080，说明所建立的模型可以较为准确地预测FRP约束矩形钢管混凝土长柱的轴压承载能力．

通过对比试验现象和有限元分析结果，分析了长柱在轴压荷载下的破坏模态及受力机理．

(1) 在承受轴向压力时，钢管沿柱高方向分布有多处外鼓变形，整体呈正弦半波分布．无约束钢管混凝土柱的破坏模态主要有两种：一种是钢管在端部严重鼓曲，该处混凝土被压碎，试件在端头发生转动、弯折；另一种是钢管在距端部1/4高度处严重鼓曲，核心混凝土被压碎，试件整体压弯变形．

(2) FRP约束钢管混凝土柱的破坏形式与无约束试件类似，钢管的局部屈曲整体较无约束试件滞后，破坏以鼓曲最严重处的环向FRP断裂为标志．且与FRP约束圆钢管混凝土柱[9]相比，由于倒角的存在，应力集中现象在钢管角部表征明显，因此断裂均从角部开展．由于柱身整体弯曲较小，仍为全截面受压，故纵贴FRP几乎未参与受力．

(3) 有限元模拟分析得到的FRP约束钢管混凝土长柱轴压荷载-位移曲线可分为弹性段(开始加载至屈服点)、弹塑性段(屈服点至峰值点)以及下降段(峰值点之后)3个阶段．对于内填普通强度(C40)混凝土的钢管混凝土柱，环向FRP在承载力上的提升作用较明显，方、矩形截面试件的峰值荷载分别提高了7%和6%．对于内填高强度(C80)混凝土的钢管混凝土柱，整体荷载-位移曲线趋势相似，但下降段较陡，反映了其脆性大的特点，方、矩形截面试件承载力分别提升了4%和5%．

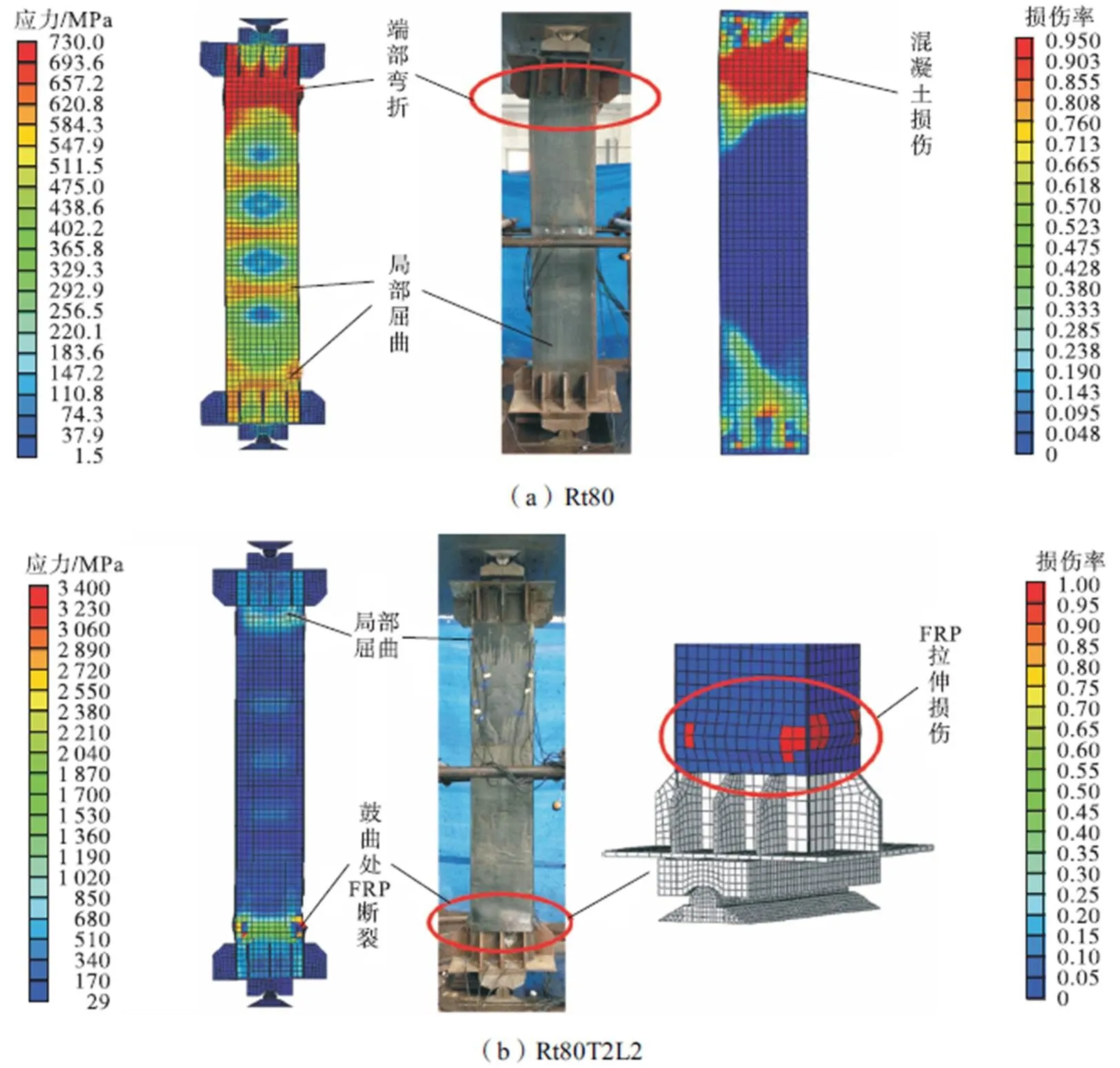
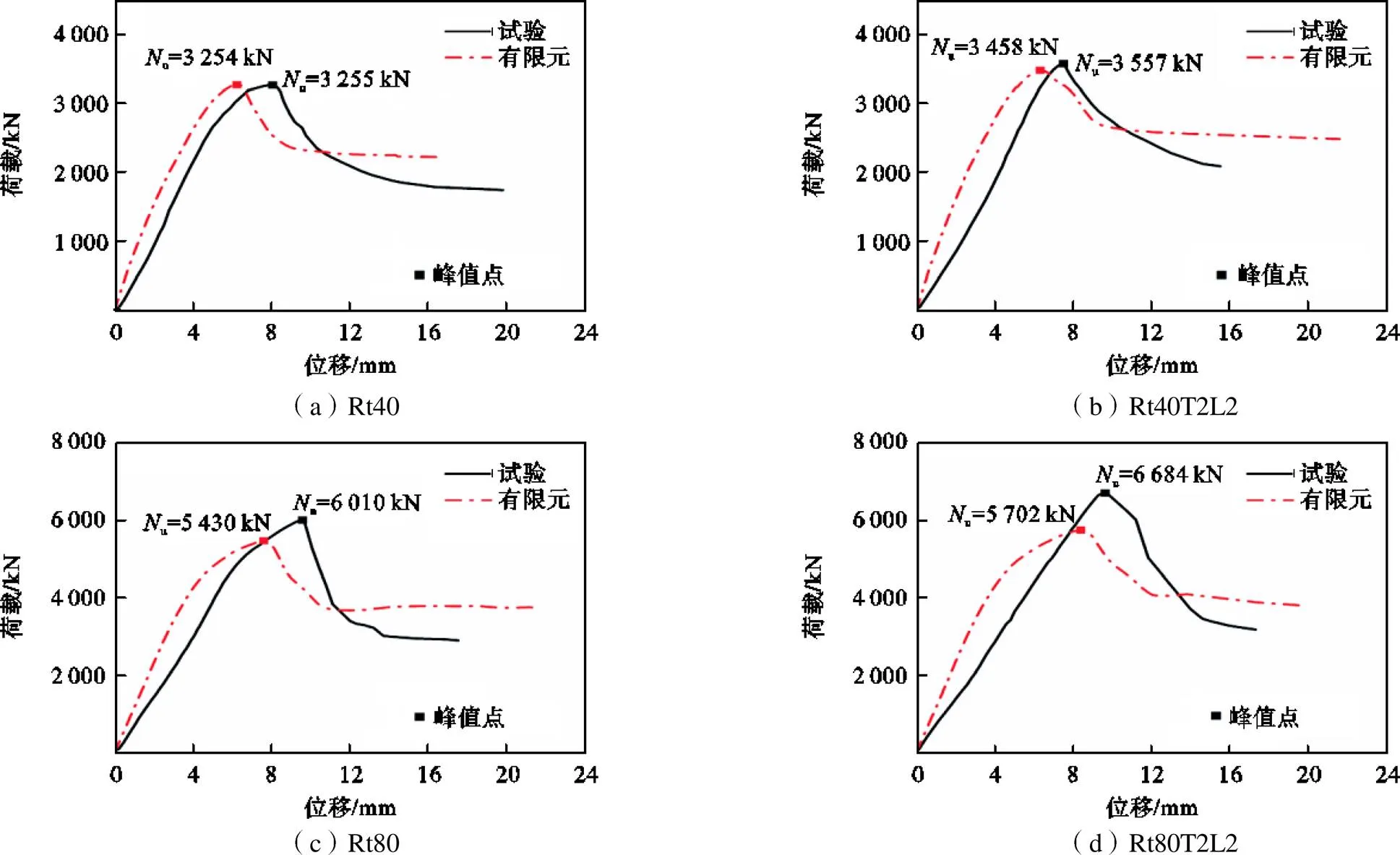
表4 试件峰值荷载与有限元结果对比

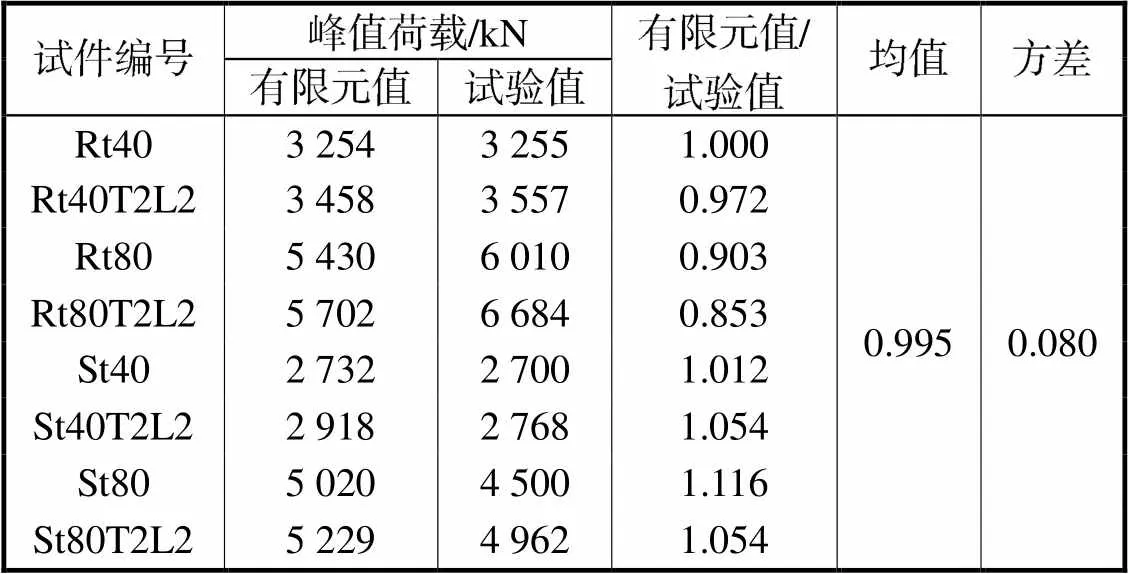
Tab.4 Comparison of peak load and finite element results

4 长细比参数化分析

矩形钢管混凝土柱在承受轴向荷载时，其受力特点与破坏形式受构件长细比影响较大．当长细比较小时，构件表现为强度破坏；当长细比较大、构件发生整体失稳时，截面极限强度不能充分发挥，构件表现为稳定破坏，其承载能力将发生折减．矩形钢管混凝土轴心受压柱的长细比计算式为

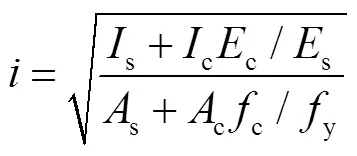
式中：0为柱的计算长度；为截面回转半径；s、c分别为钢管和混凝土的截面惯性矩．

为了弥补试验过程中对长细比因素研究的不足，特设计了4种不同长细比的有限元模型，内填C60混凝土，为了减小倒角的影响和利于网格划分，将有限元模型的倒角半径和钢管壁厚分别设为20mm和4mm，设计参数见表5．

典型短柱和长柱的破坏模态分别如图12所示．如图12(a)所示，短柱在轴压荷载下表现为强度破坏，截面应力对称分布，混凝土可以充分发挥抗压强度．长柱表现为失稳破坏，如图12(b)所示，柱中部或中上部产生较大的侧向挠度，荷载发生偏心，混凝土在破坏前表现为全截面受压；当压应力较大侧的混凝土达到强度极限时，混凝土被压碎，柱发生破坏，此后截面出现受拉侧；环向FRP均在钢管外鼓处的角部发生断裂．

表5 不同长细比时的模型参数

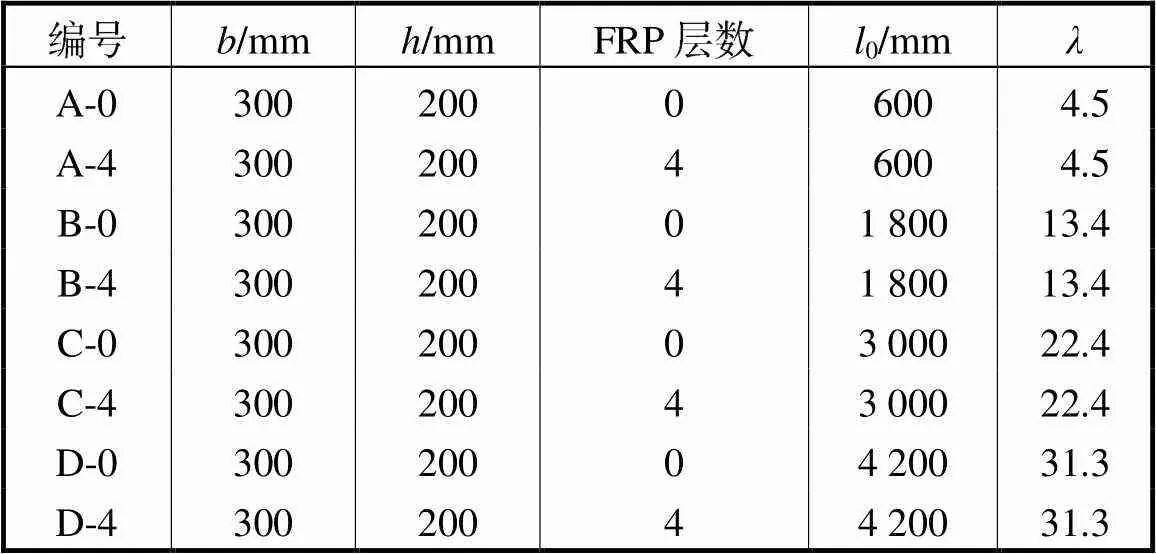
Tab.5 Parameters of models with different slenderness ratio

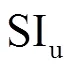
图12 破坏模态及混凝土截面应力分布

表6 长细比的影响

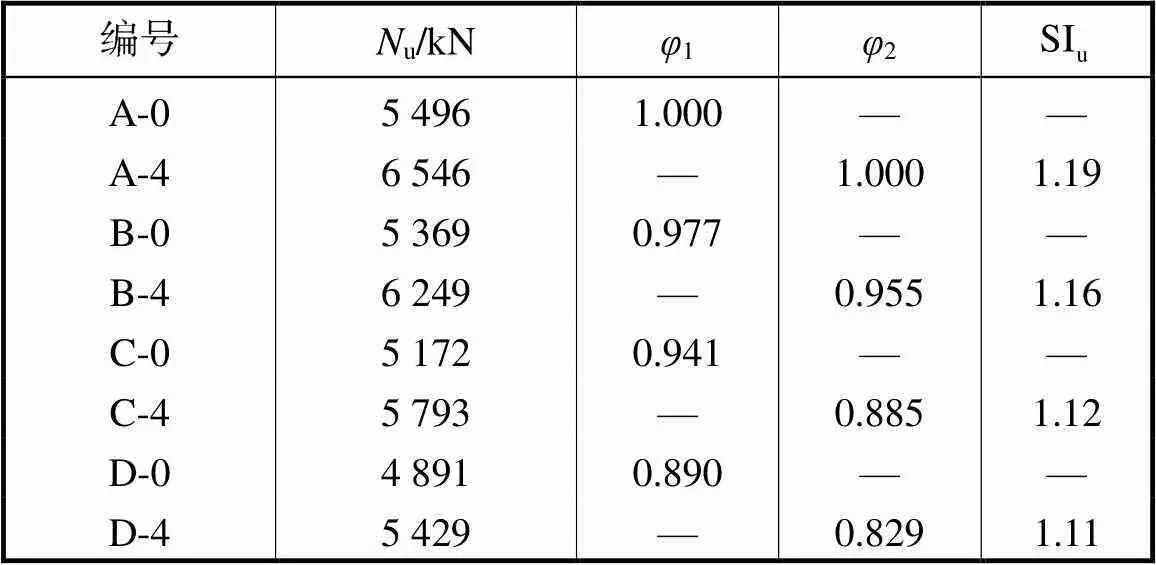
Tab.6 Effect of slenderness ratio

注：1为无FRP约束长柱峰值荷载与A-0的比值；2为FRP约束长柱峰值荷载与A-4的比值；为FRP对柱峰值荷载的提升系数．

图13 相关系数随长细比的变化规律

5 结 论

(1) 通过有限元模拟得到的试件加载现象和破坏模态与试验结果基本吻合，模型荷载-位移曲线整体趋势与试验曲线吻合良好．有限元计算得到的初始刚度略大于试验值，分析原因是由于人工浇筑的混凝土存在孔隙、不够密实导致结构刚度偏小．8组长柱试件峰值荷载的有限元模拟值与试验值之比均值为0.995，方差为0.080，说明本文采用的有限元模拟方法是准确有效的，可以基于此进一步开展研究．

(2) 基于试验和有限元模拟分析了FRP约束矩形高强钢管混凝土长柱轴压试验的受力机理：在轴压荷载作用下，薄壁钢管在纵向应力较小时就已发生局部屈曲，钢管外鼓加剧后将失去对核心混凝土的约束作用；核心混凝土在鼓曲处的塑性应变迅速发展，直至压碎开裂发生破坏．与圆形截面不同，由于矩形和方形截面存在倒角，环向FRP在钢管角部发生应力集中现象，纤维受拉损伤从角部萌生，在达到抗拉强度后发生断裂并退出工作．

(3) 对于采用不同强度混凝土的FRP约束钢管混凝土长柱，其荷载-位移曲线在整体上趋势相似，但采用C80混凝土的长柱曲线下降段较陡，反映了其脆性特点；且FRP对长柱极限承载力的提升作用随着混凝土强度的增加而降低．

(4) 短柱在轴压荷载下表现为强度破坏，长柱则发生失稳破坏．FRP的峰值荷载提升系数随着长细比的增大而降低，对于倒角半径为20mm的模型，当长细比为31.3时，环向FRP仍能为柱提供有效约束，极限承载力可提升11%．

［1］ Shen Qihan，Wang Jingfeng，Wang Jiaxin，et al. Axial compressive performance of circular CFST columns partially wrapped by carbon FRP[J]. Journal of Constructional Steel Research，2019，155：90-106.

［2］ 李黎明. 矩形钢管混凝土柱力学性能研究[D]. 天津：天津大学建筑工程学院，2007.

Li Liming. Study on the Mechanical Performance of Concrete-Filled Rectangular Steel Tubes[D]. Tianjin：School of Civil Engineering，Tianjin University，2007(in Chinese).

［3］ 李黎明，姜忻良，陈志华，等. 矩形钢管混凝土抗弯性能数值分析与简化计算[J]. 天津大学学报，2007，40(8)：990-994.

Li Liming，Jiang Xinliang，Chen Zhihua，et al. Numerical analysis of CFRT under bending load and its simplified calculating method[J]. Journal of Tianjin University，2007，40(8)：990-994(in Chinese).

［4］ 戎 贤，张祥幸，杜颜胜. 方钢管混凝土柱-H型梁新型节点倒塌性能试验研究[J]. 天津大学学报(自然科学与工程技术版)，2020，53(7)：704-712.

Rong Xian，Zhang Xiangxing，Du Yansheng. Experimental study on collapse behavior of a square concrete-filled steel tubular column-H-beam joint[J]. Journal of Tianjin University(Science and Technology)，2020，53(7)：704-712(in Chinese).

［5］ Che Y，Wang Q L，Shao Y B. Compressive performances of the concrete filled circular CFRP-steel tube(C-CFRP-CFST)[J]. Advanced SteelConstruction，2012，8(4)：331-358.

［6］ Wang Q L，Zhao Z，Shao Y B，et al. Static behavior of axially compressed square concrete filled CFRP-steel tubular(S-CF-CFRP-ST)columns with moderate slenderness[J]. Thin-Walled Structures，2017，110：106-122.

［7］ 王庆利，薛 阳，邵永波，等. CFRP约束方钢管混凝土轴压短柱的静力性能研究[J]. 土木工程学报，2011，44(3)：24-31.

Wang Qingli，Xue Yang，Shao Yongbo，et al. Study of static performance of axially compressed concrete filled square steel tubular stub columns confined by CFRP[J]. China Civil Engineering Journal，2011，44(3)：24-31(in Chinese).

［8］ 单国毅. FRP约束高强椭圆钢管混凝土柱轴压力学性能研究[D]. 广州：广东工业大学土木与交通工程学院，2020.

Shan Guoyi. FRP-Confined Concrete-Filled Elliptical High-Strength Steel Tubes under Axial Compression[D]. Guangzhou：School of Civil and Transportation Engineering，Guangdong University of Technology，2020(in Chinese).

［9］ 谭 杨. CFRP约束圆钢管高强混凝土短柱轴心受压性能研究[D]. 长沙：湖南大学土木工程学院，2016.

Tan Yang. Research on Behavior of CFRP Confined High-Strength Concrete Filled Steel Tube Stub Columns Under Axial Compression[D]. Changsha：School of Civil Engineering，Hunan University，2016(in Chinese).

［10］ 郑子晗. FRP约束矩形高强钢管混凝土柱轴压性能研究[D]. 天津：天津大学建筑工程学院，2020.

Zheng Zihan. Research on Axial Compressive Performance of FRP Confined Concrete-Filled Rectangular Steel Tube Columns with High Strength Materials[D]. Tianjin：School of Civil Engineering，Tianjin University，2020(in Chinese).

［11］ Tao Z，Wang Z B，Yu Q. Finite element modelling of concrete-filled steel stub columns under axial compression[J]. Journal of Constructional Steel Research，2013，89：121-131.

［12］ 韩林海. 钢管混凝土结构——理论与实践[M]. 3版. 北京：科学出版社，2016.

Han Linhai. Concrete Filled Steel Tubular Structures from Theory to Practice[M]. 3rd ed. Beijing：Science Press，2016(in Chinese).

［13］ 杜颜胜. 高强钢矩形钢管混凝土柱理论分析及试验研究[D]. 天津：天津大学建筑工程学院，2017.

Du Yansheng. Theoretical Analysis and Experimental Study on Rectangular Concrete-Filled Steel Tube Columns Using High-Strength Steel[D]. Tianjin：School of Civil Engineering，Tianjin University，2017(in Chinese).

Finite Element Analysis of Axial Compression Behavior of FRP Confined Rectangular High-Strength Concrete-Filled Steel Tubular Long Columns

Du Yansheng1, 2，Gao Dinghui1，Chen Zhihua1, 2，Zheng Zihan1, 3

(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；3. Tianjin Municipal Engineering Design & Research Institute，Tianjin 300372，China)

The nonlinear finite element analysis of fiber reinforced polymer(FRP)confined rectangular high-strength concrete-filled steel tubular(RHCFST)long columns was performed using the finite element software ABAQUS based on axial compression test of FRP confined RHCFST long columns. The finite element analysis results agree well with the load-displacement curves and failure modes of the test，with an average deviation and variance of peak load is only 0.5% and 0.080，respectively，exhibiting the accuracy of modeling methods such as material constitutive relation，element type，contact，and boundary conditions. The results indicate that the finite element model can accurately predict axial compression behavior. Based on the test and numerical simulation，the stress mechanism of the columns was analyzed. Although compressive stress is low，the thin-walled steel tube exhibits local buckling. The concrete develops plastic strain and lateral deformation at the most critical part of the bulge of the steel tube owing to the small corner radius. The FRP sheets have stress concentration at the corner and eventually break at the most severe bulge. Lateral FRP confinement postpones the initiation and development of local buckling of steel tubes and improves the confinement strength of core concrete. For concrete-filled steel tubular(CFST)columns filled with ordinary-strength(C40)concrete，the effect of lateral FRP on the bearing capacity is obvious. Here，peak bearing capactity of square and rectangular section specimens is increased by 6%—7%. For the CFST columns filled with high-strength concrete(C80)，peak bearing capacity of square and rectangular sections is increased by 4%—5%. Finally，the influence of slenderness ratio on axial compression behavior was explored using a finite element model. The results show that the improvement effect of FRP on bearing capacity decreases as the slenderness ratio increases. Even with a large slenderness ratio(31.3)，FRP can still provide effective lateral constraints for columns and increase the peak bearing capacity by 11% for the model with a corner radius of 20mm.

fiber reinforced polymer(FRP)；high-strength concrete-filled steel tubular long columns；axial compression behavior；nonlinear finite element analysis；slenderness ratio

TU398.9

A

0493-2137(2022)01-0066-11

10.11784/tdxbz202103058

2021-03-30；

2021-05-13.

杜颜胜（1989—  ），男，博士，讲师，duys@tju.edu.cn.

陈志华，zhchen@tju.edu.cn.

国家自然科学基金资助项目(51808182)；国家博士后科学基金资助项目(2020M670680).

Supported by the National Natural Science Foundation of China(No.51808182)，the China Postdoctoral Science Foundation(No.2020M670680)

(责任编辑：金顺爱)